基于MCTS-HM的重型汽車多參數運行工況高效構建方法

文繼澤，張 曼，，林 楠，施樹明

（1.西安工業大學機電工程學院，西安 710021；2.吉林大學交通學院，長春 130022）

長途貨運占有交通運輸行業很大的市場份額，重型汽車作為長途公路運輸的主要工具，相比于輕型汽車，不但具有較大比例的燃油消耗量，也是污染物的來源。當前，為提高車輛效率和減少環境污染，車輛智能化的發展產生了許多可供選擇的新技術。例如，多種替代燃料、節能動力系統等被嵌入重型汽車中，并逐漸提高了重型汽車的市場滲透率。其中，燃油消耗和污染物排放的評價，以及采用新技術的重型汽車整車開發與測試環節等均需要構建車輛運行工況。然而，不同于常行駛于城市和郊區道路環境的輕型汽車，用于長途載貨運輸的重型汽車常行駛于高速公路環境，車輛行駛速度高，且行駛環境往往涵蓋平原、丘陵、山地、高原等道路條件。考慮到道路坡度對評價和測試的影響不能忽略，很有必要構建滿足工況質量條件且具有高生成效率的重型汽車多參數運行工況。這將有利于提高測試和評價的有效性和準確性，為一系列重型汽車新技術的發展打下基礎。

BHATTI等和TOPI?等基于馬爾可夫鏈蒙特卡羅方法，將多參數的行駛工況狀態離散化，馬爾可夫鏈狀態包括車輛速度、車輛加速度和道路坡度。利用隨機生成方法，分別設計了城市公交車和電動車在坡道上的行駛工況，生成工況不僅反映出隨機駕駛特性，而且達到與原始數據庫很高的一致性。然而，高速坡路工況不同于城市坡路工況，多參數工況的離散狀態相對較多，利用馬爾可夫的隨機性，一般多次隨機生成也較難實現工況特征指標閾值要求。岳柄劍等和ZHAO Bolin等研究了面向重型汽車高速坡道行駛的工況構建，基于包含道路坡度信息的行駛數據，采用單純的馬爾可夫鏈方法計算速度、加速度和道路坡度的狀態轉移矩陣，發現工況狀態空間巨大，即使經過長時間的隨機生成，有些工況特征指標仍不令人滿意。這說明工況狀態個數、有限工況時間長度、工況質量設計要求等均影響該方法的設計效率。CUI Yuepeng等和YUAN Mengfei等利用HM與馬爾可夫鏈結合的方法，構建了城市坡道典型行駛工況。但是，高速公路行駛工況片段長，離散行駛工況狀態的連接處仍要按照行駛狀態轉移規則連接，然而純啟發式方法常隨機地施加到工況狀態序列上，導致被作用后的工況狀態序列出現異常跳躍的速度和加速度。最后獲得滿足代表性質量要求的工況序列概率極低，生成效率變低。

對此，為了構建滿足工況質量目標條件且具有高生成效率的重型汽車多參數運行工況，針對現有純隨機的HM會破壞工況行駛特征，從而出現生成效率低的問題，本文通過描述代表性行駛工況生成問題，提出改進的多個HM，并結合當下的學習方法——蒙特卡洛樹搜索選擇更合適的HM，進一步提高工況生成效率。

1 代表性行駛工況描述

由于期望的工況序列要求滿足與原始數據庫行駛特征一致，所以選擇包含速度類［怠速時間比例，p/%；平均速度，/（m·s）；平均行駛速度，/（m·s）；行 駛 速 度 標 準 差，/（m·s）］、加速度類［加速時間比例，/%；勻速時間比例，/%；減速時間比例，/%］、動力學類［單位距離上的正加速動能，PKE/（m·s）；速度和加速度聯合概率分布相關系數，/%］、坡度類［平均爬坡度，%；平均下坡度，%］等共11個評價指標，以此表征行駛工況特征。

工況質量要求，即將工況構建目標看成是工況序列要滿足與原始數據庫指定評價指標的相對偏差閾值約束，具體表達為式為：

式中：為生成工況，s；為原始行駛數據評價指標值；為生成工況的評價指標值；為允許偏差；為評價指標個數。

為將多目標函數轉化為單目標函數，將式（1）歸一化為式（2）；并使用滿意準則函數，具體為式（3），最終獲得單目標函數，如式（4）所示。

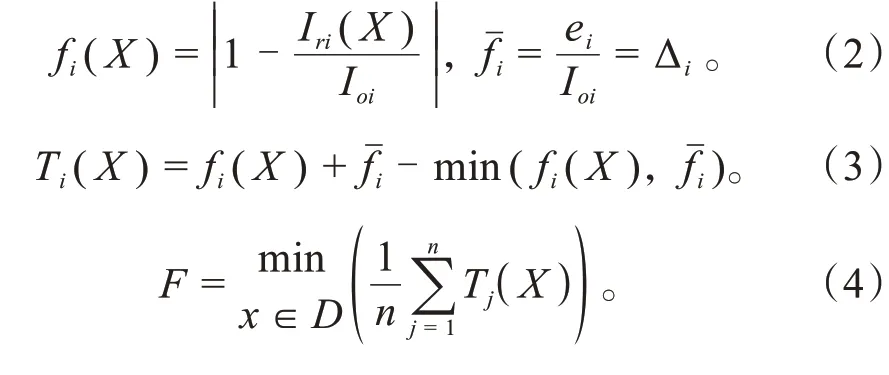
式中：為滿意準則輔助函數；為工況狀態；為工況狀態空間；為生成工況的目標函數。例如，當設置相對偏差目標閾值Δ為0.1時，對應目標函數值為0.1的工況即為最優工況。最終將求解期望運行工況問題轉化為有限時間長度的工況序列滿足指定評價指標相對偏差值閾值約束的優化問題。

2 多參數行駛工況構建方法

HM是求解期望工況優化問題的常用方法，但基于純隨機性的HM會破壞工況狀態特性，需要改進HM，同時進一步提高收斂到期望工況的效率，本文提出基于MCTS-HM的多參數行駛工況構建方法框架，如圖1所示，具體為利用傳統馬爾可夫鏈隨機模擬方法生成有限時間長度多參數行駛工況序列的種群；通過改進的多個HM被作用后的工況序列仍滿足行駛工況動態轉移特性，以此更新工況狀態序列；采用MCTS來決定在一個迭代過程選擇哪些HM用于改進當前工況序列，并使用指數蒙特卡羅作為接受準則，判斷是否接受應用HM后的工況序列。反復迭代更新工況種群，直至輸出最優工況序列。

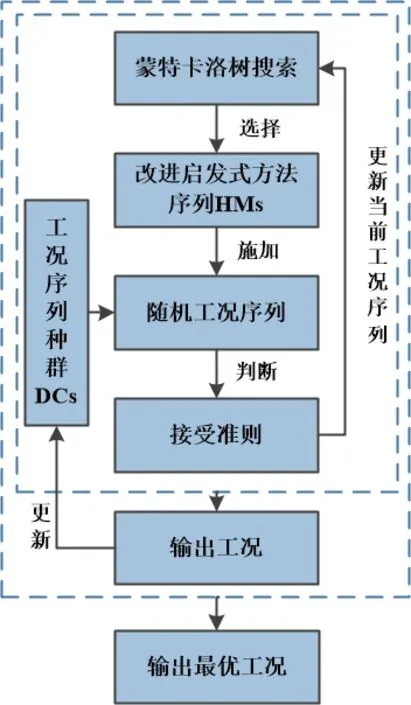
圖1 基于MCTS-HM的多參數行駛工況構建方法框架

2.1 基于改進啟發式的工況狀態更新

為了盡可能地通過多種方式使工況序列更快接近目標工況，需要設計滿足行駛工況動態轉移特性的HM。

本文試圖通過擾動當前的工況序列提高工況質量。借鑒交叉思想，交換一定長度的不同工況片段設計HM，交換點處要求滿足多參數工況狀態轉移特性，具體如下。

設為當前工況序列，為隨機運行工況序列，如式（5）和式（6）所示。

式中：，∈(1，2，…，N)；N為工況序列長度；為工況狀態；P為當前迭代次數下的工況種群；為種群大小，初始工況序列種群通過馬爾可夫鏈模擬方法得到。

基于交叉思想的啟發式方法設計如下：

首先，設定有限工況片段長度；其次，將中任意長度的工況片段替換中任意長度的工況片段；最后，生成新工況序列X，如：

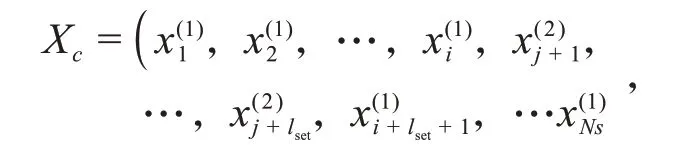
同時滿足以下約束條件：

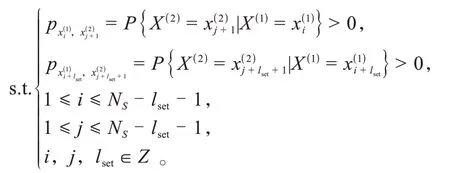
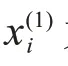
2.2 基于MCTS的目標工況高效生成

為了進一步提高工況質量，需要尋找作用到工況序列上合適的HM，運用MCTS方法進行智能決策，將HM的搜索空間建模為1個樹，搜索樹的每個結點代表1個啟發式，搜索樹表示啟發式搜索空間。因此，MCTS的4個步驟具體如下。

（1）選擇：從根結點開始，運用上限置信區間（Upper Confidence Bound，UCB）選擇要添加到當前樹路徑的HM。在當前迭代次數下，父結點有個子結點，根據UCB值按如下式（7）選擇最合適的啟發式。

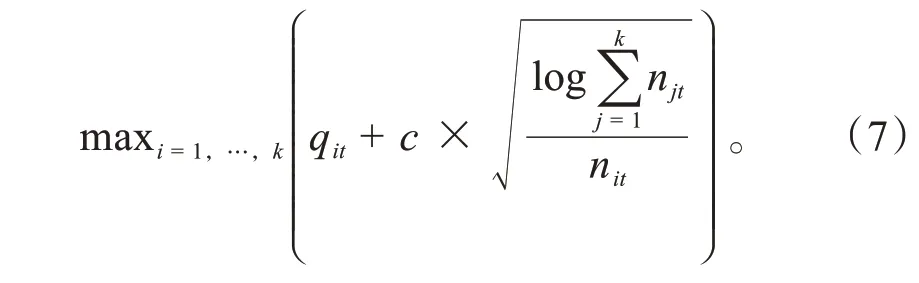
式中：為比例因子；n為當前迭代次數下第個子結點的啟發式被選用的次數；q為當前迭代次數下第個子結點的經驗評估值，即累積評估值，如式（8）所示。

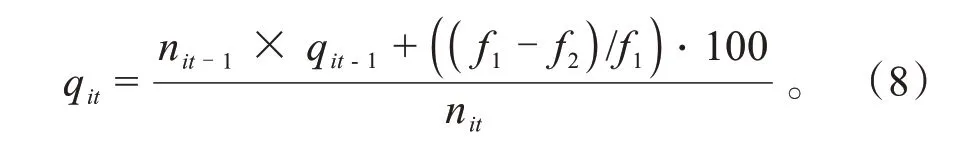
式中：（（-）/）·100為第個子結點將該啟發式施加到當前工況序列后工況函數值的變化；為當前工況的函數值；為當前工況應用該啟發式后的函數值，迭代選擇最佳子結點直至達到葉子結點，即未選用過的啟發式結點。此過程輸出為啟發式序列。

（2）擴展：為了探索啟發式空間的新區域，隨機選擇1個未探索的結點（一個不包含在當前的部分樹路徑中的啟發式），并將其添加到當前的部分樹路徑中。

（3）模擬：從生成樹路徑的葉子結點開始，將結點的啟發式施加到給定工況序列中，根據工況序列函數值的改進，采用指數蒙特卡洛（Exponential Monte Carlo，EMC）作為接受準則，判斷是否接受該工況序列，依次操作直到根結點。

（4）更新：使用式（8）更新從葉子結點到根結點路徑中每個結點的經驗評估值和選用次數。

在啟發式對工況序列進行改進的同時，工況序列種群要更新。具體來說，在每次迭代中，從工況種群中隨機選擇一條工況，將蒙特卡洛樹路徑識別的最優啟發式序列依次應用于該工況，并根據以下方式更新工況種群，采取3種隨機更新規則。

（1）如果新的工況序列質量優于工況種群中最差的工況序列，可用它取代最差的工況。

（2）無論新的工況序列質量是否變優，均將取代工況種群中最差的工況序列。

（3）無論新的工況序列質量是否變優，新的工況序列將被工況種群外隨機生成的工況序列所取代。

前兩種規則重點優化工況種群，第3種規則重在促進工況多樣性，并防止陷入局部解。

3 結果分析與討論

3.1 試驗數據采集

試驗數據來源于某用戶駕駛某型號重型牽引車在坡道頻繁的山區高速公路上行駛的數據，其行駛路線如圖2所示。車輛從中國長春市空載行駛至磐石（標識1到標識2路段），并裝載貨物；然后載貨行駛到河北省雄縣（標識3）卸貨；再空載至保定市曲陽（標識4和標識5）重新裝載貨物，行駛經過安新縣（標識6）；最后行駛至延吉到達吉林市（標識7）卸貨。

圖2 試驗路線

車輛裝載產自奧地利的模塊化同步數據采集設備DEWE-M4S，該設備可同步獲取奧地利設備VGPS的信號（道路經緯度和車速信息）、CAN總線信號以及加速傳感器信號。數據采集頻率為10 Hz，采集參數包括速度、加速度、高程等。提取高速公路行駛數據，并經過去噪和濾波處理，再采用坡度估計方法離線計算得到已知行駛路徑時域上的道路坡度，最終得到2 980 km高速公路的有效行駛數據。

考慮到工況序列是利用馬爾科夫鏈隨機模擬生成，因此需要將工況的多個行駛參數離散化。具體如下：

行駛狀態參數設定：速度、加速度和坡度步長分別為0.5 m/s，0.1 m/s，1%；怠速狀態對應的速度區間為0～0.1 m/s，加速度區間為-0.02～0.02 m/s，坡度區間為-0.2～0.2%。速度范圍0～35 m/s劃分成71個狀態，加速度范圍-2～2 m/s劃分成41個狀態，坡度范圍-10%～10%劃分成21個狀態。將實際采集數據的三維空間狀態轉化到一維空間中，最終根據參考文獻［7］計算3個參數的狀態轉移矩陣，其二維投影圖如圖3所示。生成的多參數工況序列狀態要滿足該狀態轉移特性。工況序列長度設置為常見的1 800 s，工況序列種群大小為15。

圖3 三個參數的狀態轉移矩陣的二維平面投影

MCTS-HM方法的參數設置如下：由于工況片段長度是任意的，所以會對應大量的啟發式。本文按照交換工況片段長度將HM分成4組。可交換工況片段區間為［1，100］、［100，200］、［200，1 800］和［1 800］四類啟發式。搜索樹寬度為算子個數4，搜索樹深度設置為3，比例因子為10。工況指標相對偏差閾值設置為10%，即最優工況的函數值為0.1。在處理器型號為Intel（R）Core（TM）i7-9700K CPU，主頻為3.6 GHz，內存為32 GB配置的計算機上，利用Matlab2017a執行該方法直至輸出最優工況序列。

3.2 代表性工況的行駛特征分析

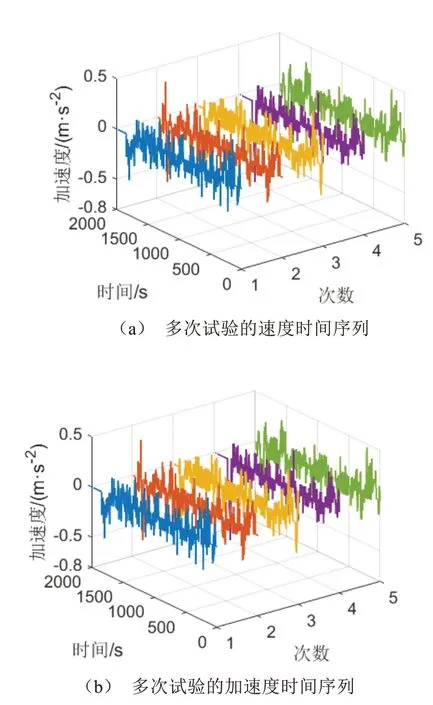
基于隨機初始工況種群以及設定的初始參數，運行MCTS-HM方法5次，直至輸出最優工況，即工況函數值為0.1時達到停止條件。期望高速公路運行工況時間序列，如圖4所示。從時間序列上觀察發現，當車輛處于爬坡時，速度會有所降低；當車輛下坡時，速度會增加，加速度處于小范圍波動狀態；平路上，車輛常保持勻速狀態。以上特征較符合期望的重型汽車高速運行狀況。

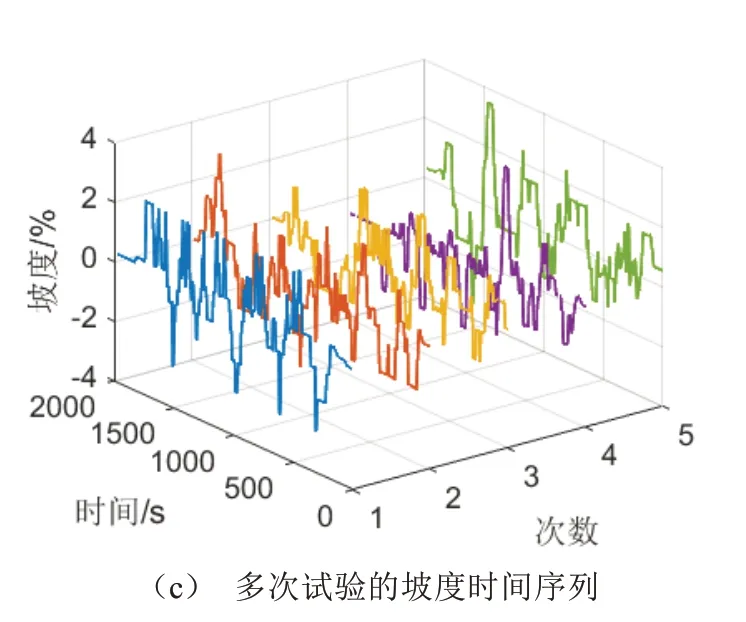
圖4 MCTS-HM運行5次的最優工況序列

此外，分析了期望工況的狀態轉移特征是否異常，如圖5所示，期望工況的狀態特征均在原始行駛工況動態轉移特征范圍內，說明期望工況均滿足原始行駛狀態轉移特征，同時驗證了提出方法的有效性。

圖5 期望工況的狀態轉移特征

多參數期望運行工況與原始數據庫的指標對比以及相對偏差絕對值，見表1和表2。該方法輸出的期望工況評價指標與原始采集數據相近，且所有評價指標的相對偏差絕對值都保持在設定閾值10%以內，速度和加速度聯合概率分布相關系數全部達到90%以上。采用MCTS-HM方法獲得的運行工況均滿足工況質量要求，以此生成的多參數工況具有代表性，可直接應用于車輛性能測試與評估。

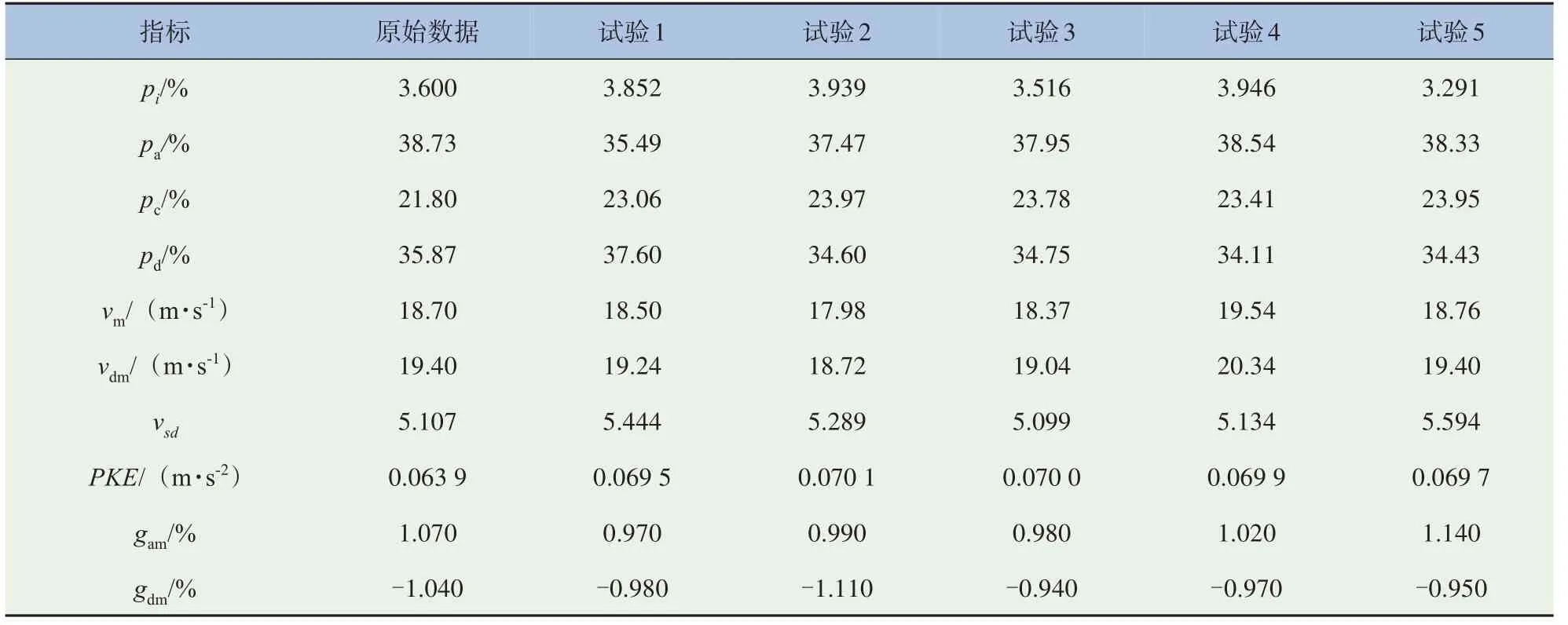
表1 MCTS-HM方法的期望工況與原始采集數據庫的評價指標

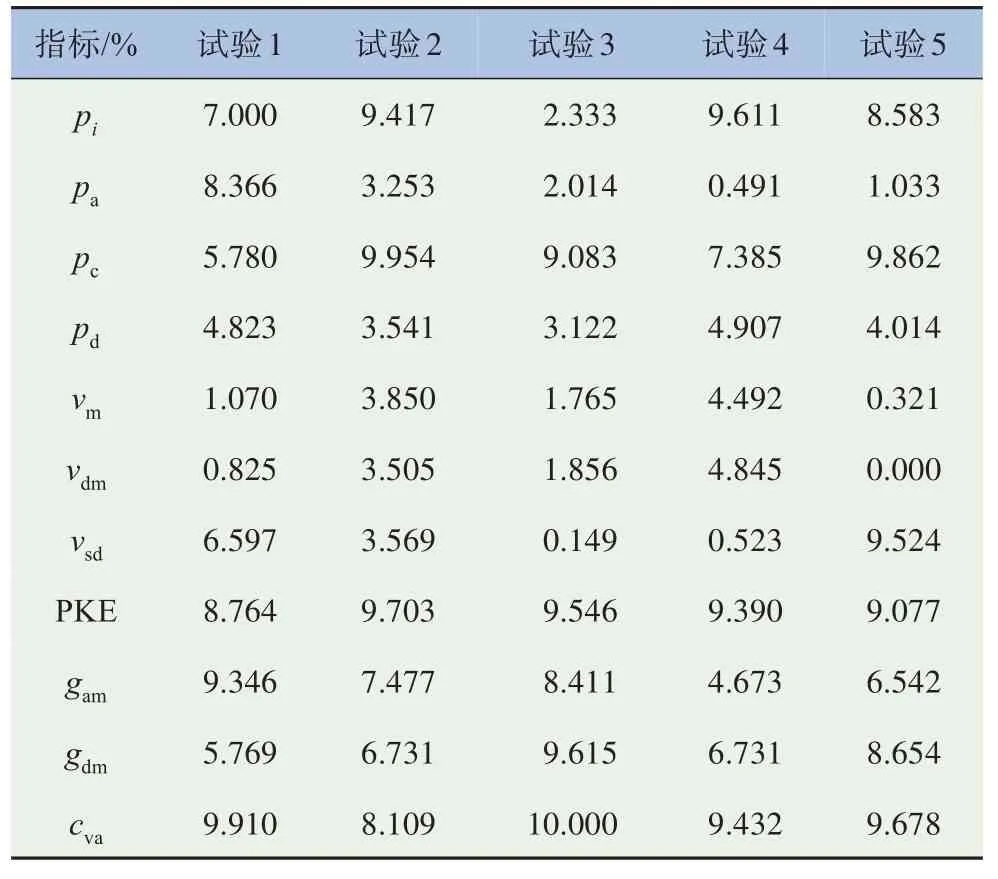
表2 MCTS-HM方法的期望工況與原始采集數據庫的評價指標相對偏差絕對值

3.3 代表性工況的生成效率分析

為分析提出方法生成最優工況的效率，在相同的行駛數據和設計目標下，本文統計隨機運行MCTS-HM方法5次直至輸出最優工況的CPU運行時間，見表3，MCTS-HM方法的CPU運行時間均值在1 100 s左右，實際用時更短，而且該用時在實際工況設計過程中是完全可接受的。然而，由于隨機性會破壞行駛工況的狀態轉移特征，致使設計效率低，所以相比于純隨機HM，提出方法不僅性能好，而且效率高。

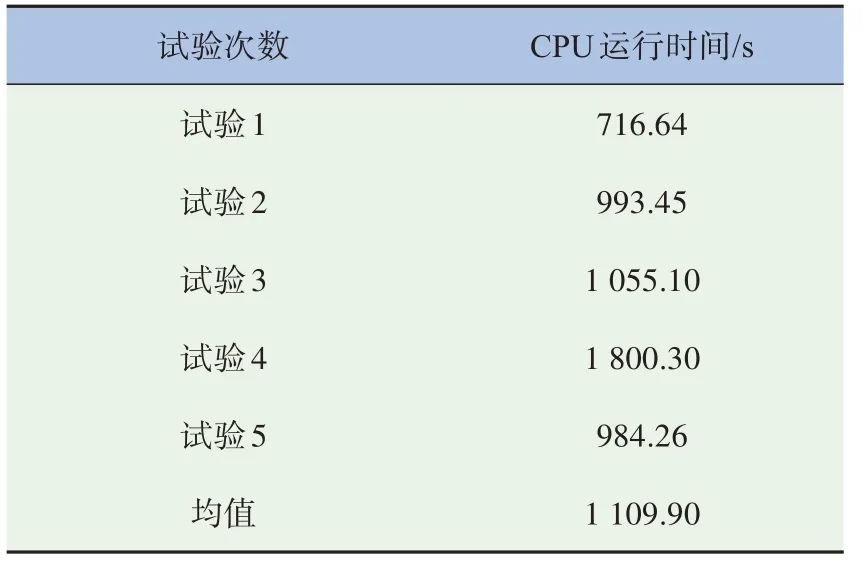
表3 隨機運行MCTS-HM方法的CPU用時

4 結論

本文提出了一種蒙特卡洛樹搜索和啟發式方法的重型汽車多參數運行工況設計方法，并利用實際采集數據進行了分析驗證，與純隨機啟發式方法相比，可以得到以下結論：

（1）由多次試驗結果分析可知，該方法獲得的多參數運行工況符合重型汽車坡道高速運行狀況特征，與原始數據庫的特征指標相對偏差均滿足所設定的閾值范圍，滿足了工況質量要求。

（2）生成工況均滿足原始采集數據的狀態轉移特征。

（3）在設定參數條件下，該方法的CPU運行時間均值為1 100 s，提出方法不僅性能好，而且效率高。

在下一步研究中，將期望工況應用于重型汽車動力性能和經濟性能評估和測試，以及動力系統參數優化等。此外，MCTS-HM的參數適用范圍取決于MCTS-HM參數對設計效果的影響，可繼續探討分析MCTS-HM各類參數對工況設計質量以及效率的影響，為實際工況設計提供參考。