基于耦合純無網格方法時間分數階下孤立子波碰撞過程的數值模擬研究*

李 悅，蔣戎戎，蔣 濤

（揚州大學 數學科學學院，江蘇 揚州 225002）

（我刊編委趙景軍推薦）

引 言

非線性耦合偏微分系統在流體力學、固體物理等領域具有重要的應用價值，其中耦合非線性Schr?dinger 系統(CNLS)[1-4]常用來系統描述兩個相互作用非線性孤立子波的碰撞過程.近年來，受分數階算子[5-8]影響的耦合非線性Schr?dinger 系統受到廣泛關注，其與整數階情況下的物理現象截然不同，比如受分數階影響出現了孤立波的塌縮現象[9].

關于分數階CNLS的數值研究，由于受非線性Schr?dinger 方程中非線性項以及分數階的影響，很難通過解析的手段得到其理論解.因此關于分數階的數值模擬方法[10-13]成為了重要的研究手段，其中大部分是基于網格類的，如有限元法[10]、有限差分法[11]、無單元Galerkin 法[12]等，這類基于網格的方法在處理局部加密以及非均勻分布時較為復雜，很難實現，而無網格方法[13]能彌補上述缺點，但對無網格方法的研究尤為罕見.

基于上述分析，本文針對TF-CNLS 方程給出一種耦合純無網格有限點集法(CFPM)[14-15].該方法的基本思想是：首先，基于Caputo 分數階高精度差分格式對時間分數階項進行離散；其次，基于Taylor 展開和加權最小二乘思想，并引入雙曲余弦核函數對空間項進行離散求解，從而得到一種能夠準確數值預測TF-CNLS 方程的CFPM.數值研究結果展示了本文提出的CFPM 能夠準確地求解一維TF-CNLS 方程且具有近似二階收斂精度，并將其數值模擬結果與有限差分結果作對比，表明CFPM 能夠有效預測TF-CNLS 方程的孤立子波非彈性碰撞過程波的復雜傳播現象.

1 時間分數階耦合非線性Schr?dinger (TF-CNLS)方程

耦合非線性Schr?dinger (CNLS)方程[3]常被用來模擬離散保守系統中兩個相互作用的非線性波包.本文考慮一維情況下時間分數階耦合非線性Schr?dinger 方程：

初始條件為

邊界條件通常為周期邊界或如下邊界條件：

其中uk(k=1,2)是兩個極振中的復值波振幅，i=是虛數單位，η是線性雙折射的歸一化強度，參數 λ描述了群速度色散，β是跨相位調制.

分數階導數[16]的定義有很多種，其中Riemann-Liouville 和 Caputo 分數階導數是近年來最常用的兩種分數階微積分方法，本文主要采用Caputo 分數階導數.

定義1設 α是一個正實數，令q-1＜α＜q,q為一個正整數.函數f(t)定 義在區間 [a,b]上，其 α階Caputo 分數階導數形式為

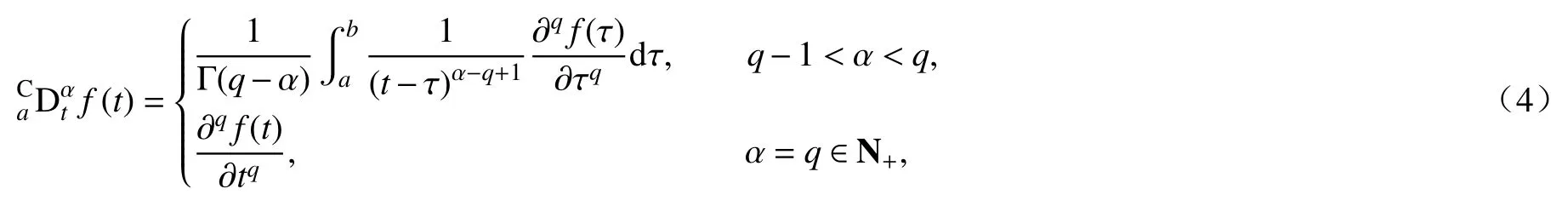
其中t∈[a,b].易知

其中算子 Γ(·)是Gamma 函數，即為廣義的階乘，且允許取非整數及復數值.

2 CFPM 離散格式

本文針對TF-CNLS 方程的模擬研究，基于Caputo 分數階高精度差分格式與FPM 離散格式進行耦合，給出一種具有較高精度和穩定性的CFPM 來模擬TF-CNLS 方程.其思想是：首先，應用3 -α精度的Caputo 導數形式對時間項進行處理；其次，采用具有較好穩定性的雙曲余弦核函數[17]推廣應用FPM 對空間導數項進行二階顯式離散.

2.1 基于Caputo 導數時間分數階離散格式

根據文獻[18-19]，目前針對基于Caputo 分數階導數的差分格式常見的有：“2-α”(L1 型)和“3-α”(L1-2 型).本文采用精度較高的L1-2 型格式，并與顯式FPM 耦合求解TF-CNLS 方程.在本小節中，引入時間項誤差為O(Δt3-α)的L1-2 型格式.

設tn=nΔt,tn+1/2=(tn+1+tn)/2，其中n=0,1,2,···,Δt是時間步長.定義差商算子：

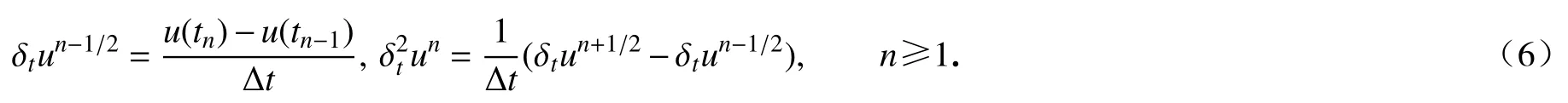
u(t)∈C1[0,tn](n≥0) α(0＜α＜1)

假設，根據定義可知，對于任意的有

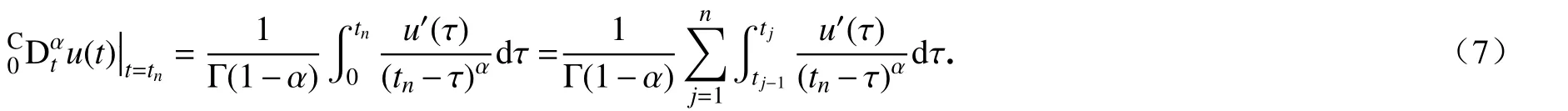
設插值函數Π1,ju(t)=由線性插值理論可知

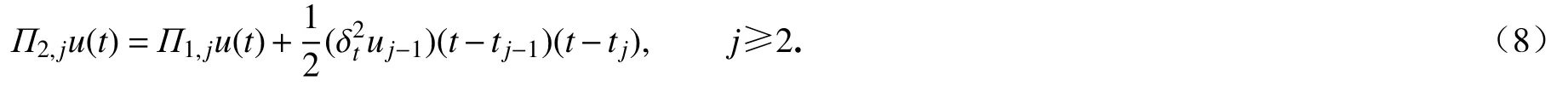
對于函數u(t)，我們可以得到一個新的α (0＜α＜1)階Caputo 分數階導數的數值近似，形式如下：

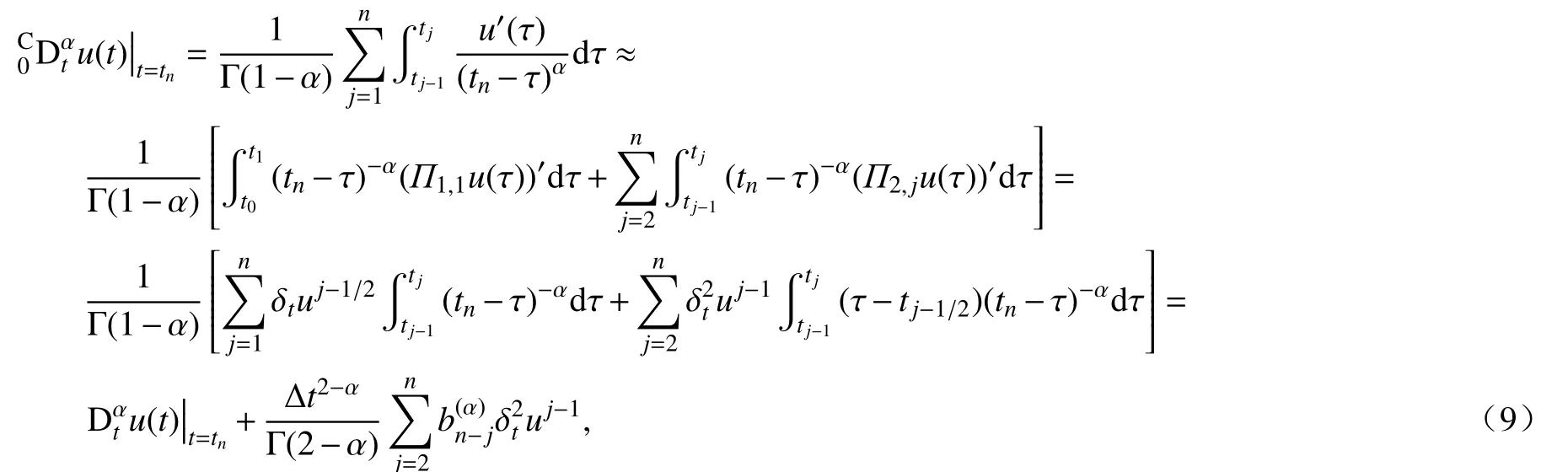
其中系數

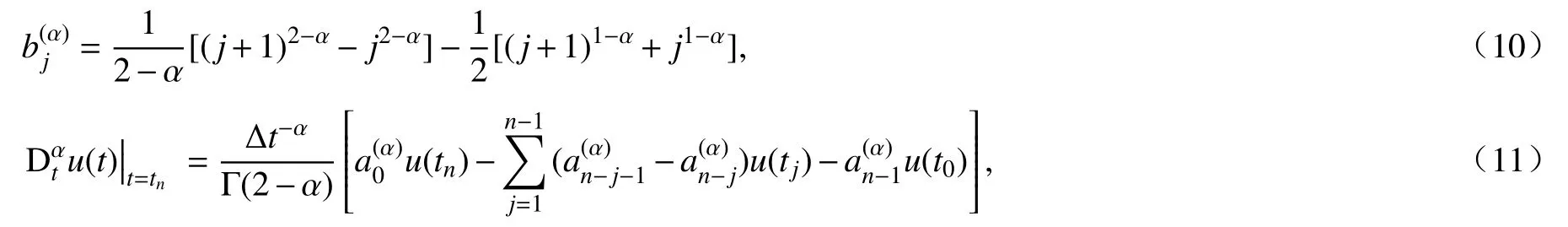
引理1[19]對于任意α (0＜α＜1),設

近似格式(7)可以寫成

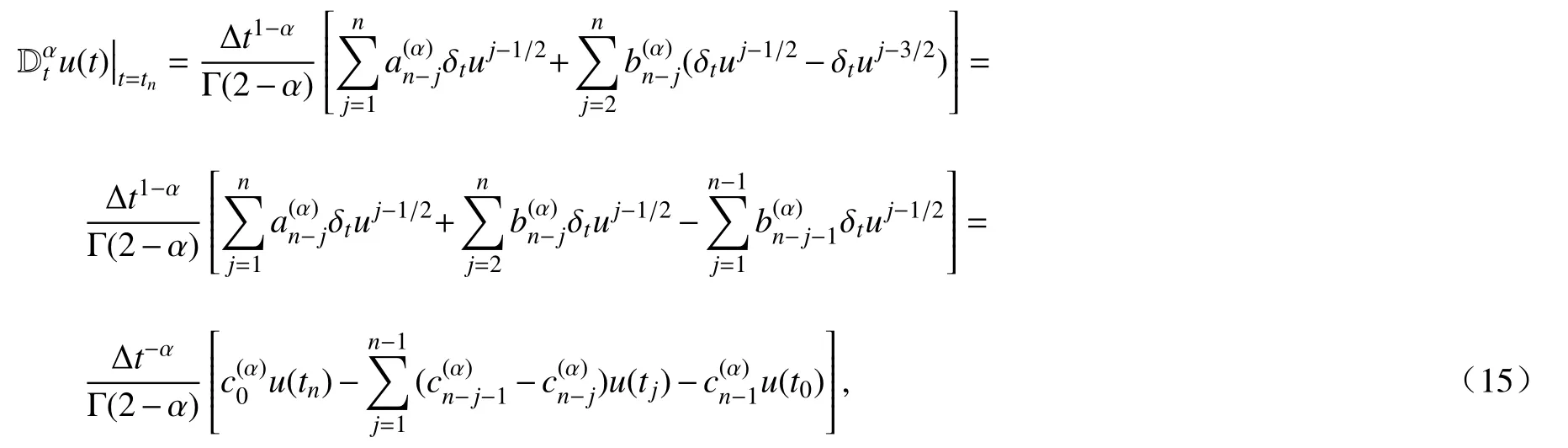
其中

系數{}滿足以下性質.

引理2[19]對于任意 α(0＜α＜1)，式(15) 中(0≤j≤n-1,n≥3)，則

2.2 空間導數FPM 離散格式

FPM 常被用來求解方程(1)，直接應用基于Taylor 展開和加權最小二乘思想[18-19]的顯式FPM 對一、二階空間導數項進行離散求解.設未知函數為u(x)，求解區域為? ?Rd(d=1)，區域內的任意節點為xi(i=1,2,···,N)(N為節點總數)，引入加權最小二乘對函數在x處的一、二階導數進行離散近似.加權最小二乘中選取雙曲余弦核函數[17]，其形式如下：

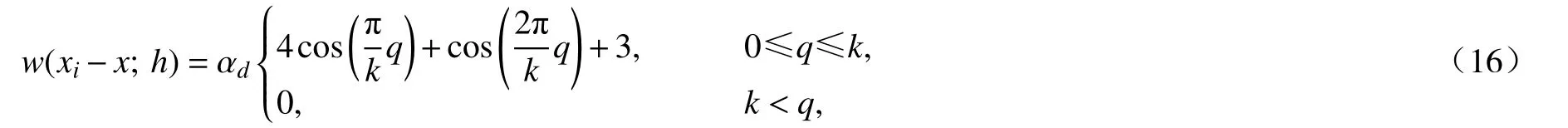
其中q=rij/h,rij=|||xi-xj|||，αd是正常數，一維情況下αd=1/(6kh)，h為光滑長度，此處取h≈0.95×d0(d0為初始距離)，支持域范圍是以2.5h為半徑的圓.

考慮支持域內相鄰節點xi(i=1,2,···,m)在x處Taylor 展開，可得

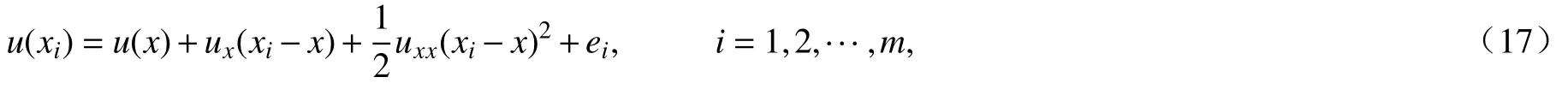
其中ei是Taylor 展開式的誤差余項.式(17)可化為

其中

dxi分別表示xi-x(i=1,2,···,m).

通過誤差ei加權最小二乘法對未知函數u的一、二階導數進行求解，可得

J=(Ma-b)TW(Ma-b)Ww1w2···,wm

式(19)可以寫成，其中為對角矩陣，對角線元素為，,.

根據J的極小值原理，得到

式(20)涉及2×2 局部系數矩陣，函數的一、二階導數值可通過其近似求得.

為保證數值方法的穩定性，本文選取的時間步長 Δt≤0.1d02(d0為節點初始距離)通常滿足限制性條件(見文獻[15,20]).

由此可得方程(1)的CFPM 離散格式為

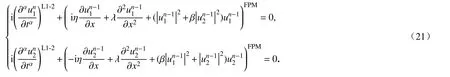
注1在CFPM 離散過程中，空間層采用Taylor 展開以及加權最小二乘思想，其截斷誤差具有近似二階精度[14]；時間層采用精度較高的Caputo 分數階導數L1-2 型格式，具有3 -α階精度[15].

3 數值收斂性分析

本節采用帶解析解的一維二分量時間分數階非線性Schr?dinger 方程，對本文提出的CFPM 求解TFCNLS 方程的數值精度和收斂性進行了分析討論.

定義均方根誤差(ERMS)和收斂階(Cr)為

其中ui,Ui分別為第i個節點的數值結果和解析解，d1,d2為不同節點的初始間距.

考慮區域?=[0,2π]上具有周期邊界的非齊次TF-CNLS 方程[21]，對應的方程為

iDαt u(x,t)+iux+uxx+u+v+2(|u|2+|v|2)u=f1(x,t),

iDαt v(x,t)-ivx+vxx+u-v+4(|u|2+|v|2)v=f2(x,t),

初值條件為u(x,0)=0,v(x,0)=0，相應的強制性項為

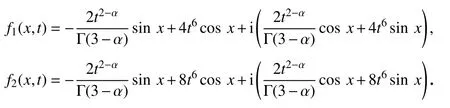
對應該方程的解析解為

u(x,t)=t2(cos(x)+isin(x)),v(x,t)=t2(cos(x)+isin(x)).

通過對算例的模擬，圖1和表1～3 體現了本文給出的CFPM 模擬TF-CNLS 方程的數值收斂速度以及靈活可靠性.圖1展示了 α=0.7，均勻分布情況下，時間步長為Δt=10-3，不同時刻下CFPM的數值模擬結果，并與解析解作對比，可以看出CFPM的數值模擬結果與解析解一致.表1和表2分別列出了不同α（α=0.9,0.7），t=1.0 時刻不同節點數情況下，三個不同物理量的RMS 誤差和收斂階.從表1和表2可以看出，所給的CFPM 數值模擬TF-CNLS 方程是趨于二階精度收斂的.

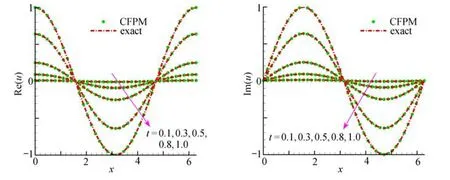
圖1 α=0.7，不同時刻下Re(u)，Im(u)的解析解與數值解Fig.1 The exact and numerical solutions of Re(u) and Im(u) with α=0.7 at different moments

表1 α=0.9，t=1.0 時刻下的RMS 誤差和收斂階Table 1 The RMS errors and convergence rates with α=0.9 at t=1.0

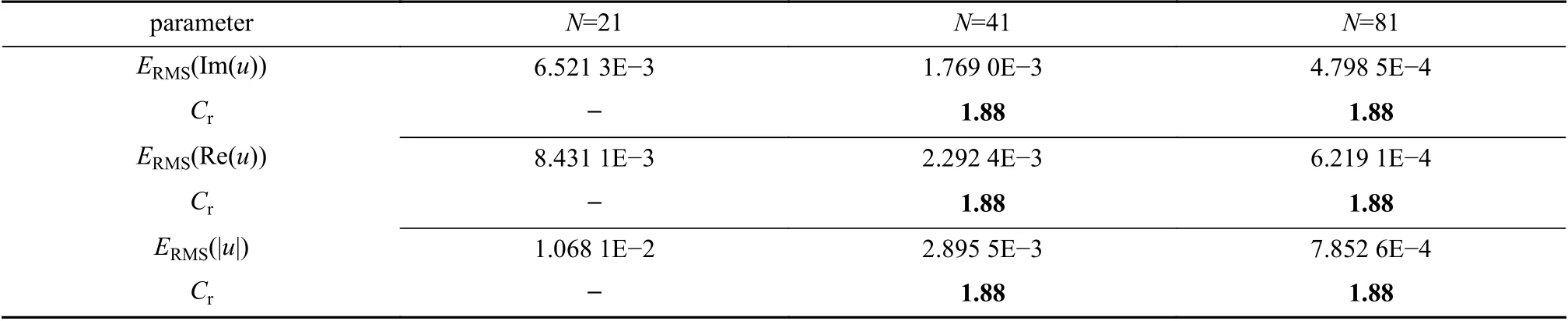
表2 α=0.7，t=1.0 時刻下的RMS 誤差和收斂階Table 2 The RMS errors and convergence rates with α=0.7 at t=1.0

在[0,π/5],[9π/5,2π]處節點局部加密，使得該區域的空間步長為粗節點分布處的一半，其余區域仍采用節點均勻分布方式，時間步長為Δt=10-4，兩種分布方式的臨界點光滑長度為h≈0.5×(0.95×d1+0.95×d2).表3列出了 α=0.7時，部分時刻下均勻分布與局部加密分布情況下的RMS 誤差.由表3可知，節點均勻分布的誤差稍大于局部加密時的誤差.因此，給出的CFPM 易推廣到局部加密情況，具有較好的靈活推廣應用性.

表3 α=0.7 時，不同時刻下均勻分布與局部加密情況下的RMS 誤差Table 3 The RMS errors of uniform distribution and local refinement with α=0.7 at different moments

4 時間分數階下孤立波非彈性碰撞過程數值預測

本節主要研究了兩種不同邊界條件下(周期邊界和Dirichlet 邊界)，無解析解TF-CNLS 方程描述孤立子波的非彈性碰撞過程，對其進行了數值預測，并與有限差分方法(FDM)進行對比，以驗證數值預測的可靠性.所采用的有限差分方法具有二階精度(詳見文獻[22]).

4.1 周期邊界下TF-CNLS 方程

考慮區域?=[-40,40]上的TF-CNLS 方程[2]，其對應的方程為

iDαt u+βuxx+[λ1|u|2+(λ1+2λ2)|v|2]u+γu+Γv=0,

iDαt v+βvxx+[λ1|v|2+(λ1+2λ2)|u|2]v+γv+Γu=0,

初值條件為

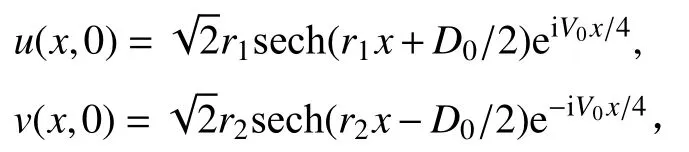
其中系數 β=1,λ1=1,λ2=2,γ=Γ=0，r1=r2=1,D0=20,V0=1.周期邊界條件為u(x,t)=u(x+80,t)，v(x,t)=v(x+80,t).

本小節運用CFPM 對該算例進行了數值預測，圖2給出了t=30時，不同α下，CFPM 和FDM的數值模擬結果.從圖2可以看出，分數階情況下的孤立子波的峰值減小并變寬，且CFPM 與FDM的數值結果擬合.因此，給出的CFPM 能夠準確模擬預測TF-CNLS 方程.

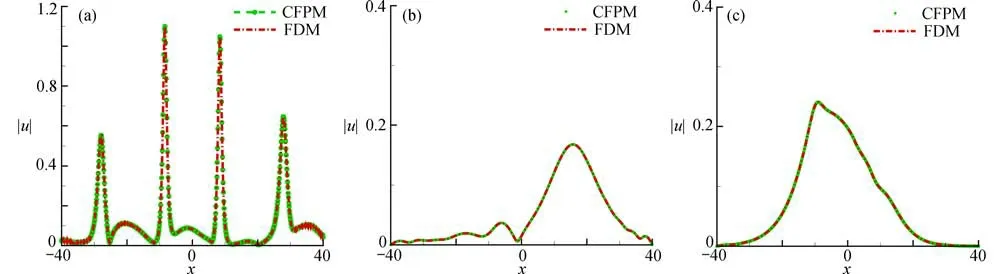
圖2 t=30 時孤立波函數|u|的數值結果對比： (a) α=1.0；(b) α=0.9；(c) α=0.7Fig.2 Comparisons of the numerical results of isolated wave function |u| at t=30: (a) α=1.0; (b) α=0.9; (c) α=0.7

圖3給出了CFPM的數值模擬結果，時間步長為Δt=10-6，其中圖3(a)是整數階情況下的數值結果，圖3(b)、圖3(c)分別是α=0.9,α=0.7時的CFPM 數值模擬結果.由圖3所有數值結果可以看出，時間整數階下在碰撞之后出現了四個孤立波，分數階情況下的孤立子波在非彈性碰撞過程中出現了復雜的傳播現象，該現象與文獻[9]中波的塌縮現象類似，且與整數階現象截然不同.

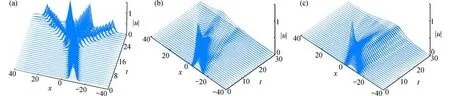
圖3 CFPM 對孤立波函數|u|的數值結果：(a) α=1.0；(b) α=0.9；(c) α=0.7Fig.3 Numerical results of the CFPM for isolated wave function |u|: (a) α=1.0; (b) α=0.9; (c) α=0.7

4.2 Dirichlet 邊界下TF-CNLS 方程

為體現提出的CFPM 求解帶Dirichlet 邊界TF-CNLS 方程的準確性，本小節考慮區域?=[-40,40]的一維二分量TF-CNLS 方程，其對應的方程[3]為

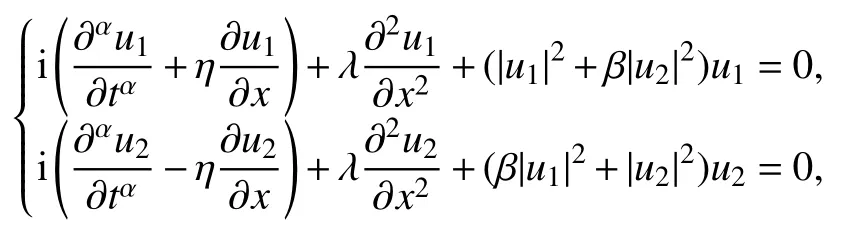
初值條件為

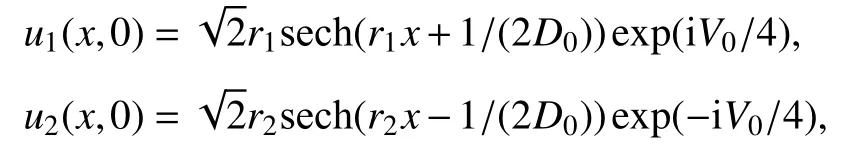
其中 η=0,λ=1,β=2/3,V0=1.3,D0=25,r1=r2=1.

本小節采用提出的方法對該算例進行了數值預測，圖4給出了不同α下，t=30時，CFPM 和FDM 對孤立波函數 |u1|的數值模擬結果.從圖4可以看出，CFPM 與FDM的數值結果一致，由此表明本文的數值研究是可靠的.

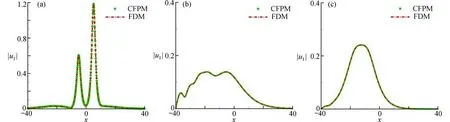
圖4 t=30 時刻下，孤立波函數|u1|的數值結果對比： (a) α=1.0；(b) α=0.9；(c) α=0.7Fig.4 Comparisons of the numerical results of isolated wave function |u1| at t=30: (a) α=1.0; (b) α=0.9; (c) α=0.7

圖5和圖6給出了CFPM的數值模擬結果，時間步長為Δt=10-6，其中圖5是不同α 下孤立波函數 |u1|的數值預測結果，圖6是不同α下孤立波函數 |u2|的數值預測結果.圖5和圖6展示了整數階和時間分數階TFCNLS 方程的孤立波傳播現象，可以看出兩種情況下的現象是顯然不同的，整數階下波在碰撞后出現了兩個孤立波，而時間分數階下出現了波的塌縮現象，其現象相較于整數階更為復雜.

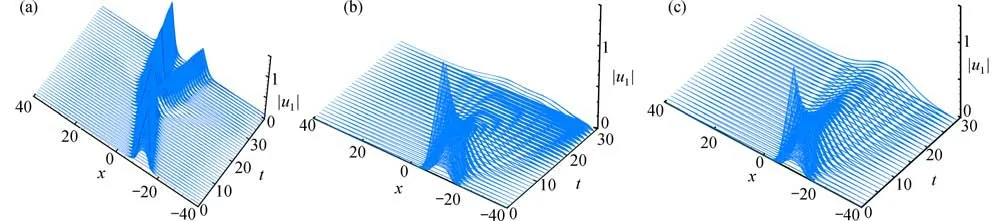
圖5 CFPM 對孤立波函數|u1|的數值結果：(a) α=1.0；(b) α=0.9；(c) α=0.7Fig.5 Numerical results of the CFPM for isolated wave function |u1|: (a) α=1.0; (b) α=0.9; (c) α=0.7

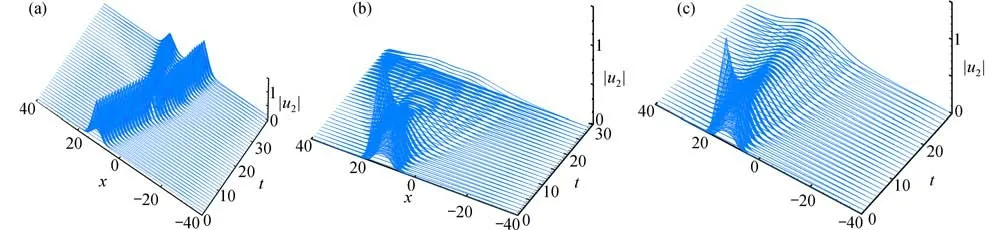
圖6 CFPM 對孤立波函數|u2|的數值結果：(a) α=1.0；(b) α=0.9；(c) α=0.7Fig.6 Numerical results of the CFPM for isolated wave function |u2|: (a) α=1.0; (b) α=0.9; (c) α=0.7

由此可見，耦合非線性Schr?dinger 方程在時間分數階下出現了波的塌縮現象，整數階下出現了多波現象，這兩種現象截然不同；且CFPM 模擬預測TF-CNLS 方程的現象與有限差分結果相吻合.因此，給出的CFPM 模擬預測TF-CNLS 方程是準確的.

5 結 論

本文針對時間分數階耦合非線性Schr?dinger 方程的數值預測，首次將Caputo 分數階導數的一種高精度差分格式和FPM 離散格式進行耦合，提出了一種能夠準確預測TF-CNLS 方程下孤立子波非彈性碰撞過程的純無網格方法(CFPM).數值研究中，首先對提出的CFPM的數值收斂速度進行了驗證和分析，并體現了該方法在非均勻分布情況下易實施的優點.然后，對受時間記憶效應影響的孤立子波非彈性碰撞過程進行了數值預測，并與FDM 結果作對比.通過數值模擬可知：

1) 給出的CFPM 對一維TF-CNLS 方程的求解具有近似二階精度；

2) 對局部加密與均勻分布兩種情況下的數值誤差進行了討論，表明所提出的純無網格方法在區域離散上具有靈活推廣應用的優點；

3) CFPM 預測時間分數階下孤立子波非彈性碰撞過程出現的波塌縮現象與時間整數階下截然不同，并與FPM 結果比較，表明本文的數值預測結果是可靠的.

因此，本文所提出的CFPM 能夠準確、可靠地預測TF-CNLS 方程下孤立子波非彈性碰撞過程中的復雜傳播現象，也為時間記憶效應下孤立子波非彈性碰撞過程的純無網格法模擬提供了依據.