基于高級程序設計語言的高職數學課程可視化教學探索*

段 敏

（湖南交通職業技術學院，湖南 長沙 410132）

1 引言

公共數學課程作為高職院校理工科專業必修的基礎課程，教學的核心目標之一就是培養和發展學生的數學分析思維和工程問題建模能力[1]。然而，由于理論知識具有高度抽象性，現有大學數學課程教學普遍偏重計算能力的培養而忽視學生數學分析思維的培養。在這種教學模式下培養出來的學生往往不知道如何將實際問題轉化成數學模型問題加以分析和解決，缺乏運用數學知識進行分析的思維，在解決復雜的實際問題時數學建模能力不足。

隨著計算機軟件技術的飛速發展，數學課程教學也逐漸引入計算機進行輔助，并針對其進行了大規模的教學改革實驗。數學實驗課在1988年最早由美國雷斯勒技術學院開展實施。我國對數學實驗課的探索始于1997年，國防科技大學首次在課堂上開展了數學實驗教學，由此開始了數學教學改革。依托該項目，李尚志教授編寫了教材《數學實驗》[2]。在這之后，眾多高校開始關注數學課堂改革。然而，在現階段高職院校普遍缺少數學實驗課程的現狀下，如何將具有大量抽象理論的大學數學課程內容生動化、簡單化，調動學生學習興趣與積極性，成為了數學公共課程教學改革面臨的難題[3]。

本文提出把《高等數學》《復變函數》等高職院校公共數學課程教學過程和MATLAB、Python等高級語言程序設計軟件結合起來，借助數學建模工具強大的數值計算、分析與圖像處理功能，顯化實際問題的分析過程和解決過程，實現數學抽象理論的可視化教學，幫助學生提高數學分析思維，提高教學效果，培養學生解決復雜實際問題的能力。

2 MATLAB、Python概述

MATLAB由美國MathWorks公司開發維護，至今已有近40年的發展，其在矩陣計算和算法開發方面功能強大，而且能夠為用戶提供高級可視化工具[4]。作為一款數值計算軟件，MATLAB因其眾多優點備受師生推崇，在數學建模、矩陣計算方面尤其受到人們的喜愛。MATLAB內含大量函數庫，可隨時調用，不需要大量且繁瑣的編程過程。與其他編程軟件相比較而言，對數學語言的親和性更顯得其編程語言的簡潔優雅[5]。

Python軟件最早是由來自荷蘭的Gudio van Rossum于1989年創建開發的，由于該軟件具有良好的交互性，又是開源語言，拓展性能好，近年來熱度越發高漲，深受用戶歡迎[6]。Python是一種功能性強、語法簡單，在數學、物理、人工智能等各個領域都有廣泛應用的編程語言。其中，Sympy庫是用來進行科學計算的核心，它能夠基于符號計算體系高效完成多項式計算。Sympy庫能夠實現多種復雜計算，具有操作簡單、應用性強的特點，常被用來求解方程，尤其在計算涉及復雜數學建模問題的微分方程時常常成為首選。

3 數學課程可視化教學意義

3.1 編程成為理工科學生的必備技能

計算機技術的發展日新月異。近年來，大數據技術被廣泛運用于各行業領域，熟練掌握一門編程語言已經成為從事數據分析、數據挖掘、大數據分析、人工智能等崗位工作的標配。社會對學生編程能力的要求日益提高，逐漸從加分項演變成必修項。因此，在大學階段很有必要對學生進行編程教育。

從教學的角度來看，教師要考慮學習效果和實際應用效果，通過建模、仿真及可視化等一系列流程，能夠使學生深入思考數學原理，親自動手開展實踐以解決問題，一舉兩得。從學生的角度來看，學生對編程語言的掌握并非一朝一夕可以實現，在熟悉數學知識的基礎上開展編程的基礎學習，對專業知識、編程知識體系的構建都很有好處，能夠鍛煉學生的思考能力和實踐能力。

3.2 可視化教學改善理論教學枯燥性

教學效果因教師和學生而異。很多情況下，教師難以兼顧所有的學生，特別是在學生就業選擇各不相同的背景下，教師對課程深度和知識難度的把控很大程度上會直接影響學生的學習積極性。

通過MATLAB、Python等高級程序設計語言的圖像功能演示復雜函數理論與圖形，能夠使學生克服學習抽象理論的畏難心理，有利于學生理解和對比。教師從可視化圖形入手，由簡單知識過渡到數學原理，將理論知識以嚴謹但不失有趣的方式展現出來，能夠極大程度煥發學生的自主學習熱情，同時兼顧學生的基礎差異，改善了數學課程理論教學的枯燥性。

3.3 可視化教學提升數學建模能力

大學數學課程有3個顯著特性：抽象性較高、使用性廣泛、邏輯性嚴密。在課堂教學中教師往往只注重講解理論知識，忽略與實際應用相結合，使得學生無法獲取更多的感性認識，從而在理論的深度與應用的廣度上不能很好地結合。課堂教學不夠生動形象，導致學生解決實際問題的能力較弱。

數學課程教學以數學理論知識為主干內容，以建模工具的實例化演示為輔助，一方面通過數學專業軟件實現復雜函數可視化教學，另一方面通過數學建模軟件的使用培養學生的建模意識和編程能力。數學建模是實際問題的理想化，是聯系實際問題和數學語言的媒介。推動數學教學改革能夠間接提升學生數學建模能力，輔助學生向專業領域發展。

4 數學課程可視化教學典型案例

4.1 高等數學可視化實例

以函數y=sin(1/x)、y=x*sin(1/x)的極限為例，對初學者來說求解這兩個函數的極限是比較抽象的。這兩個函數分別涉及到無窮大和無窮小及有界函數極限的知識，在常規教學實踐中很難用語言或者板書解釋清楚。通過python的可視化展示，學生可以清晰地了解該函數的分布情況，對理解極限的概念很有幫助。

Python程序如下：

結果見圖1。x趨向于0時，函數值是在-1和1之間來回震蕩，越靠近0頻率越高，但是不會趨近于0，因為是一直在越來越快地振蕩，永不停止，極限不存在。x趨向于無窮，1/x趨向于0，sin(1/x)趨向于0，函數極限為0。

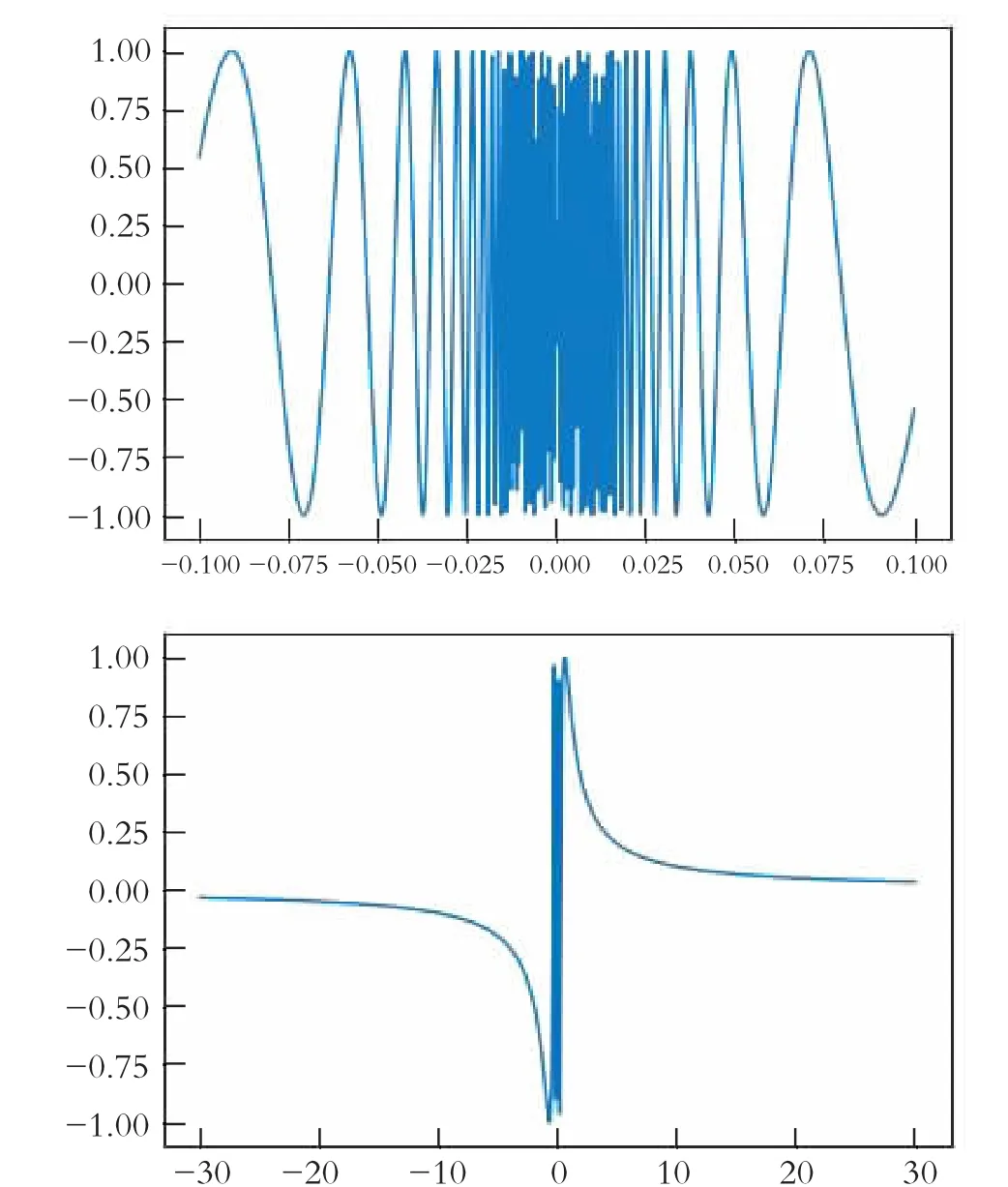
圖1 函數y=sin(1/x)的圖形

結果見第21圖2。x趨向于0時，f(x)在0上下震蕩并逐漸趨于0，極限為0。x趨向于無窮時，1/x趨向于0，f(x)趨向于1。

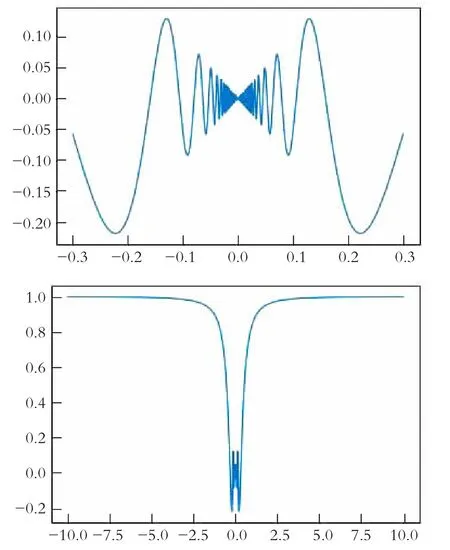
圖2 函數y=x*sin(1/x)的圖形

4.2 復變函數可視化實例

復變函數部分的內容較為晦澀難懂，其自變量和函數值中均包含復數，在圖形繪制方面難度很大，特別是要在三維空間中對上述4個實、復數進行表示，更凸顯了人們思維的局限性。在處理這部分時，MATLAB用顏色深度來處理第四維數據的變化，即采用3維+1維的形式具象化復變函數，xoy面表示自變量復平面，z軸表示復變函數的實部，顏色深度代表其虛部。

例：利用MATLAB作出復變函數f(z)=z5+z2+1的圖像。

MATLAB程序如下：

結果見圖3。

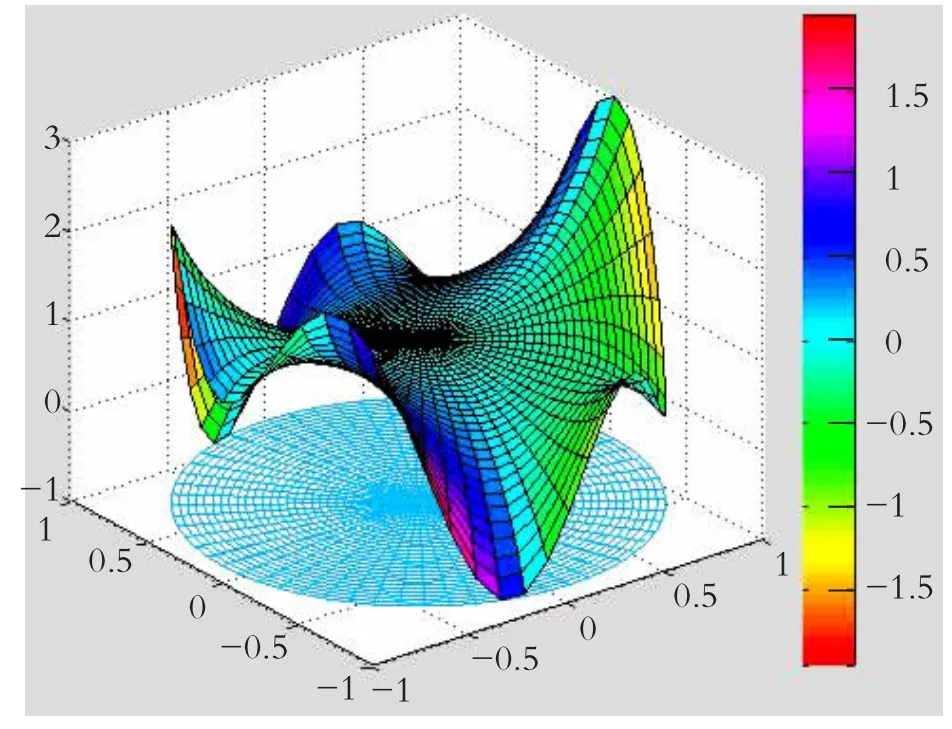
圖3 復變函數f(z)=z5+z2+1的圖像

對于某些解析函數，Taylor展開的方式方法雖然很多，但是計算較繁雜，而且Taylor展開式的結果也不一定很滿意，但是在MATLAB的幫助下，這些工作就會很簡單，調用函數就可以對其進行任意項的Taylor展開。

例：設f(z)=sin(z2/(z-1))，求f(z)在z=3處的前五項Taylor展開式。

MATLAB程序如下：

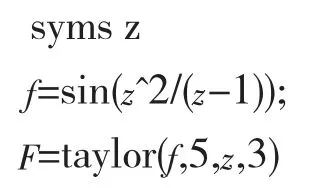
結果：

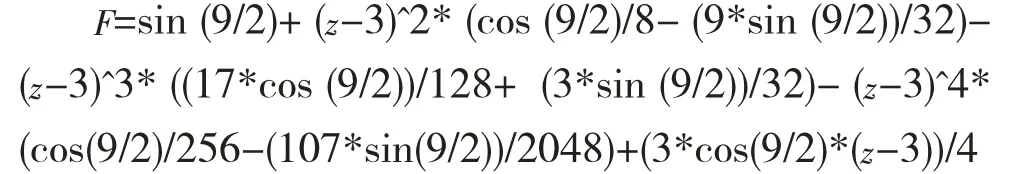
5 結論

基于高級程序設計語言強大的繪圖功能，教師不需要在課堂上進行冗長的數學理論推導，只需要引導學生分析討論解決問題的思路和處理方法，數學運算可交給數學專業軟件去進行，不但減輕了教師的負擔，而且有利于學生理解函數的概念及培養學生對于數學建模軟件的應用能力，無論是對學生課程理論知識的學習，還是對學生數學能力和建模能力的提高都具有重要意義和實用價值。