基于齒頂結構設計的面齒輪接觸性能優化

魯 銳，陳思雨，江 平，劉 波

（1.中國航發湖南動力機械研究所，湖南 株洲 412002；2.中南大學機電工程學院，長沙 410083）

0 引言

面齒輪副常用于交叉軸動力傳輸之中，主要由面齒輪和與面齒輪共軛的小齒輪組成。根據不同的工況要求，小齒輪可以設計為直齒輪、斜齒輪、錐齒輪等。由于面齒輪傳動具有結構緊湊、傳動平穩、動力分流效果好和對安裝誤差不敏感等特點，在軍用領域中經常使用面齒輪傳動代替錐齒輪傳動以實現傳動系統減質以及提高承載能力。尤其是在美軍方聯合美宇航局進行的先進旋翼機傳動（The Advanced Rotorcraft Transmission，ART）項目中，將面齒輪傳動運用到直升機主減速器中，取得了重大成功。波音公司的Apache武裝直升機使用面齒輪傳動代替傳統的弧齒錐齒輪傳動使得傳動系統的總質量減少40%，承載能力提高了35%，且分流效果好，振動小。該項目在實踐中充分證明了面齒輪傳動的優勢。隨著航空發動機高功重比/高推重比的發展，對傳動系統的承載能力要求越來越高，面齒輪在航空發動機傳動系統中具有十分廣泛的應用前景。

目前，關于面齒輪的研究大多集中于面齒輪系統的嚙合特性和加工原理方面。Litvin等對面齒輪傳動的嚙合原理、嚙合特性和加工原理做了大量研究，推導了面齒輪的齒面方程，并基于齒面接觸分析（Tooth contact analysis，TCA）的方法進行面齒輪副的嚙合特性研究；Chung T D和Chang S H建立了含有安裝誤差的直齒面齒輪分析模型，通過仿真分析得到了安裝誤差對面齒輪系統的影響；Guingand等研究了安裝誤差和加工誤差對面齒輪系統嚙合軌跡和接觸應力的影響并進行了試驗驗證；Handschuh對直升機面齒輪傳動系統的失效模式和承載能力進行了仿真和試驗，表明表面點蝕是主要失效形式，但也發生了彎曲失效，齒輪構件上均出現點蝕或彎曲引起的齒裂紋；Wu等、曹茂鵬等、唐進元等進行了面齒輪3維建模、接觸分析、面齒輪加工的系統性研究；李政民卿等利用有限元進行了面齒輪加載接觸分析。隨著有限元技術的發展，越來越多的學者采用有限元方法對面齒輪傳動進行接觸分析，計算其傳遞誤差、接觸區域和應力分布。

目前主要采用齒面修形的方法對面齒輪系統的傳動性能優化，但面齒輪修形設計與加工較為復雜，關于齒頂結構對面齒輪系統嚙合特性的影響規律罕有研究。本文針對1個存在邊緣接觸的面齒輪傳動系統，采用齒頂倒圓和削頂的方式對面齒輪齒頂進行結構修改，分析2種方式對面齒輪接觸特性的影響規律。

1 初始面齒輪模型

本文所分析的面齒輪系統基本參數見表1。基于面齒輪系統基本參數，利用有限元分析軟件對表中的面齒輪系統進行加載接觸分析，其最大接觸應力曲線和云圖如圖1所示。從圖中可見，在50 N·m的載荷作用下，面齒輪在嚙合過程中最大接觸應力為1254 MPa，已超過了材料對應的許用接觸應力1080 MPa。從圖1（b）中可見，最大接觸應力發生在面齒輪齒頂位置，是由于存在邊緣接觸而導致的應力集中。負載為50 N·m時最大接觸應力已超過材料許用應力，而在正常工況下面齒輪的負載可達1300 N·m左右，因此該面齒輪模型無法滿足實際的工程要求，需要對原模型進行性能優化。本文主要通過面齒輪齒頂倒圓和齒頂削頂的方法來提高端面齒輪傳動系統的性能。

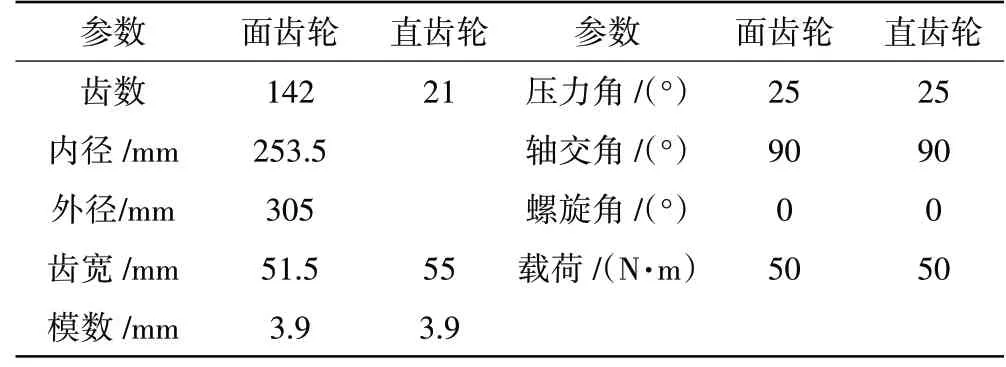
表1 面齒輪系統基本參數

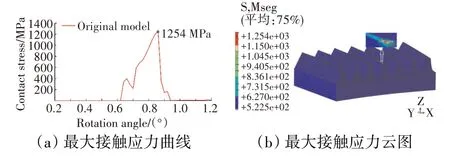
圖1 初始面齒輪模型最大接觸應力曲線和云圖

2 面齒輪齒頂結構優化設計

2.1 面齒輪齒頂倒圓對其接觸性能的影響

參考直齒輪齒頂倒圓半徑大小選擇經驗，設置了3種面齒輪齒頂倒圓半徑，見表2。其中為面齒輪模數。基于所設置的3種倒圓方案，分別進行有限元建模仿真分析，并將負載增大到1500 N·m。

表2 3種面齒輪倒圓方案

3種倒圓模型所對應的嚙合力曲線如圖2所示。從圖中可見，3種方案所對應的最大嚙合力分別為5109、4448和4788 N。此外，對于0.10模型，當輪齒即將退出嚙合時嚙合力存在突變，結合該時刻的應力云圖（如圖3所示）可知此時面齒輪發生了邊緣接觸導致應力集中所造成的。

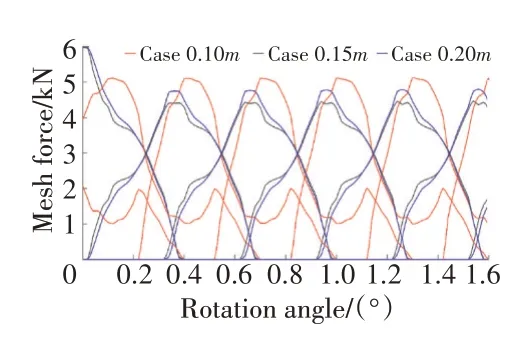
圖2 3種倒圓模型所對應的嚙合力曲線

圖3 倒圓方案1嚙合力突變點對應的應力

3種倒圓模型對應的最大接觸應力曲線如圖4所示。從圖中可見，3種模型所對應的最大接觸應力依次為2953、662和542 MPa。3種倒圓模型最大接觸應力時刻所對應的應力云圖如圖5所示。從圖中可見，0.10模型依然存在邊緣接觸，這是該模型接觸應力較大的原因；0.15模型的最大接觸應力相比0.10模型的明顯減小，但其對應的嚙合位置依舊在齒頂附近；相對于其他2種方案，0.20模型的最大接觸應力不僅明顯減小，且其對應的嚙合位置遠離齒頂。

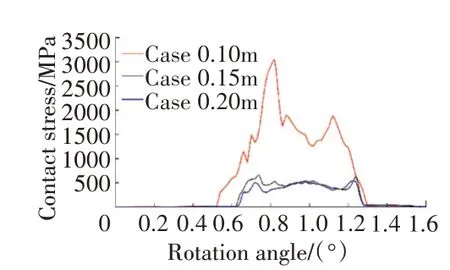
圖4 3種倒圓模型對應的最大接觸應力曲線

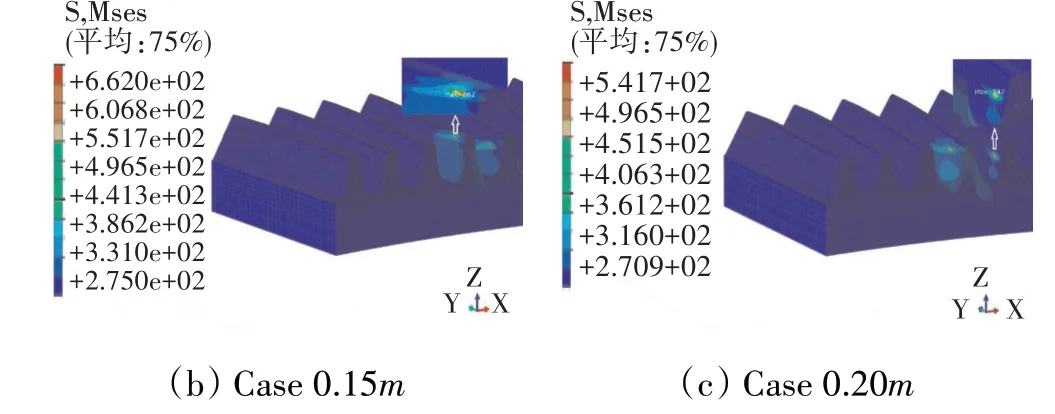
圖5 3種倒圓模型對應的最大接觸應力

根據文獻[1]提供的齒輪重合度計算方法，齒輪重合度的計算方法為

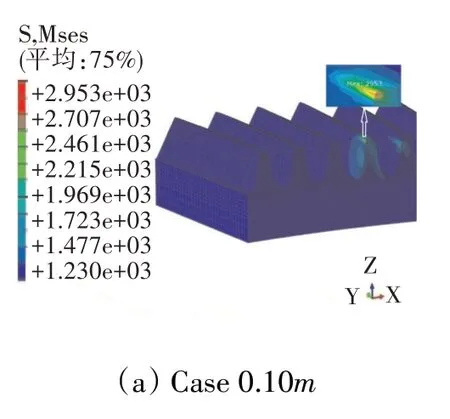
式中：Δ為單個輪齒參與嚙合對應的時間；Δ為相鄰輪齒進行嚙合的時間差。

基于有限元仿真分析結果和公式，3種模型所對應的重合度依次為2.6、2.3和2.2。可見隨著倒圓半徑的增大，面齒輪的重合度逐漸減小。考慮到隨著重合度減小，面齒輪的承載能力會逐漸降低。方案3（0.20模型）既可以避免邊緣接觸，又可以減小齒頂倒圓對承載能力的影響，為最優的齒頂倒圓方案。

2.2 面齒輪齒頂削頂對其接觸性能的影響

在經典板理論中，可以通過改變板的形狀如改變平板邊的個數、挖孔等方式來改變平板的剛度、應力等性質。基于此原理，將齒輪的齒面看作1塊板，沒削頂時是1塊矩形板；如果齒面被切掉1個角，齒面就會從四邊形變成五邊形，齒輪的性能也會相應改變。基于此假設，采用面齒輪齒頂削頂的方式對面齒輪系統進行優化。

面齒輪齒頂削頂如圖6所示。在直齒面齒輪安裝坐標系下，在平面內作與軸成角的射線。射線繞軸旋轉得到1個傘形曲面，并將曲面以上部分切掉，得到面齒輪削頂模型。本文共設置了3種削頂方案，見表3。從前文分析可知，采用0.20齒頂倒圓時面齒輪嚙合性能較好，因此對削頂模型也進行了0.20倒角。

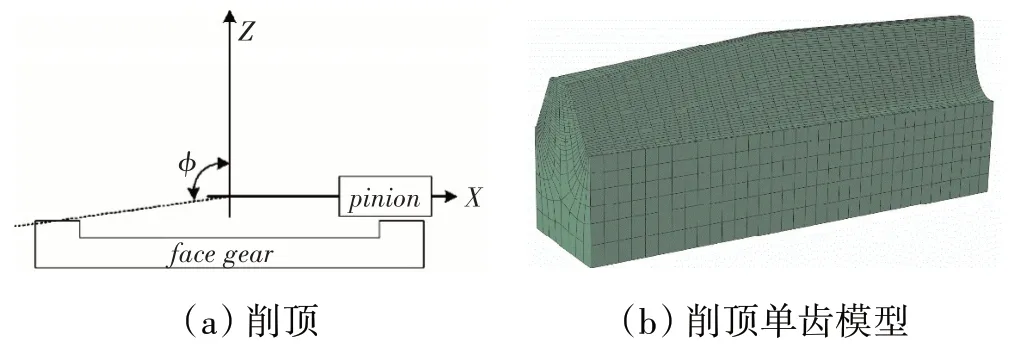
圖6 面齒輪齒頂削頂

表3 面齒輪削頂方案

3種削頂模型對應的嚙合力、最大接觸應力曲線以及應力云圖如圖7、8所示。從圖7中可見，97.2和97.5削頂模型的嚙合力曲線幾乎一致，在嚙合過程中最大嚙合力為4677 N，重合度均為2.2。與無削頂0.20倒角模型相比，嚙合力大小幾乎相同，重合度也相同。對于97.8削頂模型，其嚙合力明顯增大，最大嚙合力為5768 N，且重合度降低到2.07。從圖8中可見，97.8削頂模型的接觸應力與其他2種模型的相比非常大，其最大值達到1449 MPa，超過了允許的接觸應力。而97.2和97.5模型的最大接觸應力分別為626、535 MPa。

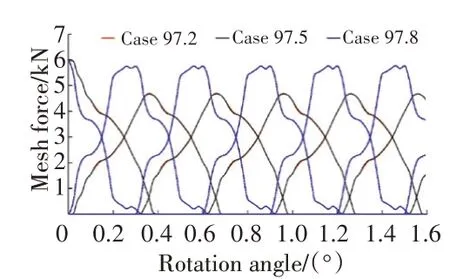
圖7 3種削頂模型對應的嚙合力曲線

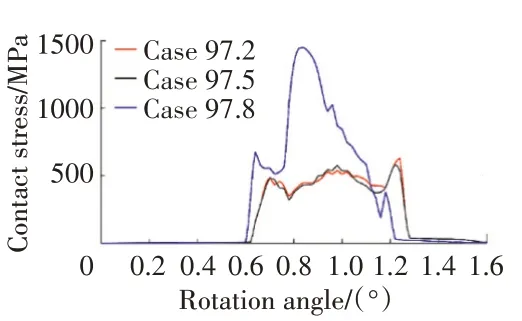
圖8 3種削頂模型對應的最大接觸應力曲線

3種削頂模型對應的最大接觸應力云圖和剛進入嚙合時的嚙合點位置如圖9、10所示。從圖中可見，97.8削頂模型的最大接觸應力出現在齒尖邊緣，而其他2種模型的最大接觸應力都在輪齒表面。因此，97.8的削頂使面齒輪嚙合出現邊緣接觸現象，這是因為較大的削頂角度改變了齒面接觸面積。此外，97.5削頂不影響接觸面積，所以嚙合力和重合度與0.20倒圓模型的相同。而97.8削頂模型改變了齒面接觸區域，因此嚙合力和重合度發生了變化。因此，削頂時必須注意削頂角度不能影響到齒輪副嚙合軌跡和接觸區域。

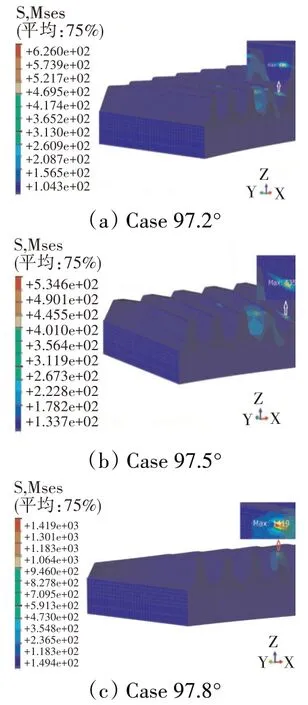
圖9 3種削頂模型對應的最大接觸應力云圖

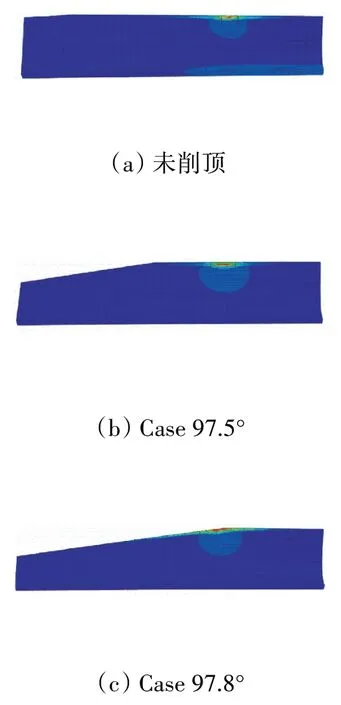
圖10 3種削頂模型剛進入嚙合時的嚙合點位置

當密度為7850 kg·m時，各削頂模型的質量和轉動慣量計算見表4。從表中可見，3種齒形切削模型的質量比原模型的分別減少了0.12%、0.8%和2.6%。對于面齒輪輕量化設計，合適的切齒是一種方便有效的方法。因此綜合以上分析，97.5削頂為最優削頂方案。

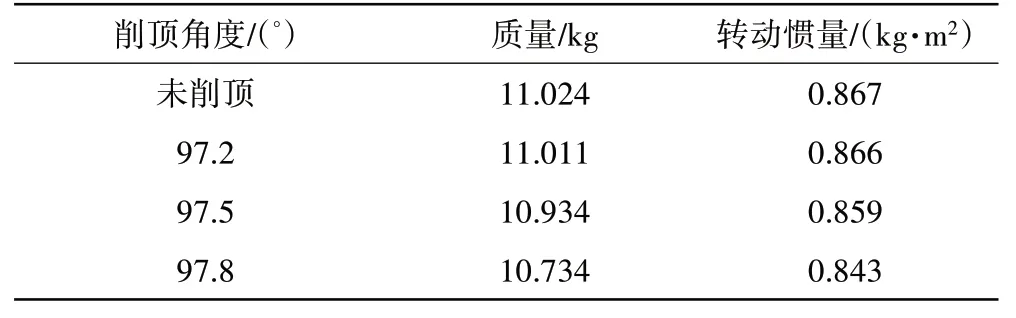
表4 削頂模型對應的質量和轉動慣量

3 結論

（1）與原始面齒輪模型相比，齒頂倒圓可以有效改善面齒輪的邊緣接觸問題和減小最大接觸應力，但隨著倒圓半徑的增大，面齒輪的重合度逐漸減小，因此齒輪倒圓存在合理的區間，通過分析發現，文中模型倒圓半徑為0.20倍模數為較優方案；

（2）削頂可以一定程度上減輕面齒輪傳動系統的質量，為系統輕量化設計提供設計方案。一定程度的削頂對面齒輪重合度和接觸應力影響較小，但較大的削頂會使齒輪發生邊緣接觸，從而使齒輪接觸應力增大。通過分析發現，文中模型削頂角度為97.5°為較優方案。