SOLO分類理論下中學生數學運算能力的培養研究

李 玉 陳思伊 陳惠汝

(黃岡師范學院,湖北 黃岡 438000)

一、問題提出

《普通高中數學課程標準(2017年版)》中指出數學核心素養是數學課程目標的集中體現，數學運算是六大數學核心素養之一數學運算是指在明確運算對象的基礎上，依據運算法則解決數學問題的素養學生從小學開始學習加減乘除，到初中學習方程，再到高中學習復雜的函數，因此，數學運算滲透到學生學習的每個階段，有著無法取代的作用由此可見，數學運算是學生解決數學問題的基本手段

歷屆高考都有對數學運算能力的考查，而考生經常出現由于數學運算能力不好而導致數學成績不佳的現象這些現象表明在高中數學教學中，部分教師自認為學生具備一定的數學運算能力，不會刻意地培養學生的數學運算能力，導致學生自己也不重視數學運算能力，將其擱置一旁在實際的教學環境中，大多數教師不會在課堂時間講解具體的運算，他們通常將解題方法或解題思路講給學生為了珍惜課堂上的每一分每一秒，他們往往選擇讓學生在課下自行計算但是對于自制力不好的學生來說，下課鈴聲一響，他們就會把課本收起來，不會再看，長此以往，他們的數學運算能力只會每況愈下

關于上述問題，許多學者提出了自己的見解劉明(2000)認為學生的運算能力是一種綜合能力，與學生的記憶能力、思維能力以及空間想象能力有著密不可分的聯系杜先存(2002)指出，學生思考問題的角度、數學運算的方式、觀察細節的能力等多方面因素對運算能力有很大的影響楊柳青(2007)認為學生對基礎知識掌握不熟練、不好的學習習慣以及錯誤的學習方法是造成學生運算能力不好的原因，并指出應該從四個方面來改善：打牢基礎、高效把握課堂、訓練良好的思維品質和訓練良好的心理承受力胡立素(2015)認為高中生數學運算能力的提升是不能速成的，需要學生慢慢積累，需要教師在日常教學中逐漸渲染運算能力的重要性武紹利(2017)認為數學運算反映了學生的數學核心素養，要想提高學生的運算能力，需要注意兩點：一點是讓學生認識到數學運算的重要性，另一點是采取運算專題訓練李琳(2019)認為教師在教學中應該規范解題步驟，重視數學運算和引導學生克服思維定式，從而培養高中生的數學運算能力

二、基于SOLO分類理論的數學運算能力劃分

SOLO(Structure of the Observed Learning Outcome)分類理論是由澳大利亞教育心理學家比格斯(Biggs)在1982年首創的一種學生學業水平分類方法.SOLO分類理論是基于學生對某一具體問題反應的分析方法，對學生解決問題時所達到的思維水平進行由低到高的5個基本結構層次的等級劃分：前結構水平、單點結構水平、多點結構水平、關聯結構水平和拓展抽象水平.

陳蓓用不同的結構圖來表示SOLO的各種水平，并結合學生的回答來判斷學生對函數概念的理解水平.王傳兵認為SOLO分類法可以讓教師了解學生對知識的掌握程度，從而進行教學反思，因材施教.艾琿璉、周瑩利用SOLO分類理論對2016年全國卷(理科)數學試卷進行分析，從高考數學試題命制和高中數學教學兩個方面提出了自己的建議.雖然各學者研究的出發點、視角存在差異性，但是可以看出，SOLO分類理論具有的理論基礎、實踐性和良好的操作性主要用于學生解決具體問題的評價，而且以知識的考查為評價重點，用知識點的組合運用水平來確定學生所處的層次，這是SOLO模型的特點.

高中課程標準修訂組的專家對六大數學核心素養做了三級水平劃分，這三種水平的劃分分別指向學業考試水平、高考水平和自主招生考試水平，每個水平中對各核心素養提出了若干要求.這是針對高中數學學習的特征劃分的，如果完全搬遷到初中數學學習中來，就會有一定的不適應性.因此，本研究在參考王光明教授2013年度教育部人文社會科學一般項目《高中生數學素養的操作定義》的基礎上，以SOLO理論的視角解讀數學運算能力水平的劃分，對各水平中的描述分別進行了分析，如表1所示.

表1 SOLO分類理論下的數學運算能力劃分

1觀察下列算式：

71=7,72=49,73=343,74=2401,75=16807,76=117649,77=823543,78=5764801,79=40353607,

……

根據上述算式的規律，請你猜想7的末位數字是________

學生空白回答，或者隨意填寫一個不相關的數字

學生通過觀察上列等式，發現7和7的末位數字一樣，7和7的末位數字一樣的規律……學生發現循環的周期為4

學生明白7的末位數字取決于190除以4的結果，經計算，190÷4=47……2因此，7的末位數字與7的末位數字一樣，即得到7的末位數字是9的結論

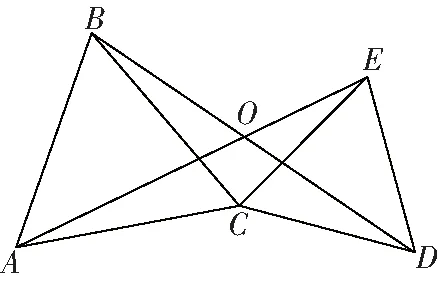
圖1

2如圖1所示，已知△，△是等邊三角形，連接，交于點，求證：∠=60°

學生空白回答，或者只把題目的條件復述一遍，并沒有證明的思路

學生根據題目中的相關條件，知道等邊三角形的三邊相等，三個角都是60°等基本信息，但是無法想到下一步的推理

學生通過等量代換，得到∠=∠，聯想到全等三角形的知識，并采用SAS來證明△≌△學生得到全等之后，得到∠=∠(對應角相等)的結論

學生通過觀察所求的角和已知的角之間是否存在聯系，意識到△與△的內角和都是180°(設，交于點)，而且有對頂角相等，加上通過全等得到的∠=∠，再次通過等量代換，可知∠和∠是等價的由此得證

關聯結構水平的學生作答如下：

∵△，△是等邊三角形，

∴∠=∠=60°

又∵∠=∠+∠,

∠=∠+∠∴∠=∠

在△和△中，

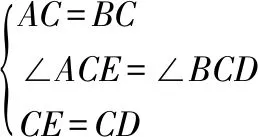
∴△≌△(SAS)

設與交于點，

在△和△中,

∵∠=∠(對頂角相等)

∠=∠(對應角相等)

∴∠=∠=60°(三角形的內角和是180°)

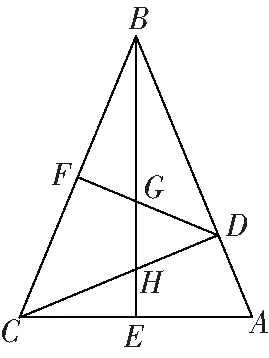
圖2

3如圖2所示，在△中，∠=45°，⊥，⊥，垂足分別為和,為中點，與，分別交于點，，∠=∠

求證:-=

進入新世紀以來，人民群眾的精神文化需求不斷升級。新聞出版業在滿足人民群眾基本閱讀需求的基礎上，還不斷致力于提升服務層次和服務水平，以滿足人民群眾個性化需求、高水平的體驗消費需求和公共文化需求。

學生空白回答，或者只把題目的條件復述一遍，并沒有證明的思路

學生根據題目中的∠=∠，⊥，知道△是等腰三角形，垂直平分，但是無法想到下一步的推理

學生再次讀題，結合∠=45°，⊥和為中點這些條件，可以推理得到△是等腰直角三角形，垂直平分學生意識到需要做輔助線將已知條件聯系起來

學生通過對求證的等式進行變形，得到=+通過觀察等式，學生發現需要證明的等式與勾股定理結構相似，遂連接

學生通過連接輔助線，可以在直角三角形中得到=+，通過垂直平分線上的點到線段兩端的距離相等，可以進行等量代換，即=，=，從而可證-=

拓展抽象水平的學生作答如下：

∵∠=∠，⊥，

∴=，是的垂直平分線

∵為中點，∠=45°，△是等腰直角三角形，

∴為的垂直平分線

連接，在⊿中，

+=

再通過等量代換，=，=，

∴-=

由以上案例可知，我們在將SOLO分類理論與具體學習內容相結合來分析學生的數學運算能力水平時，對學生數學運算能力的分析是細化的，這種細化可以幫助學生清晰地認識到自身的數學運算能力水平并找出學習側重方向，進而科學安排在數學學習中對各部分學習內容的時間分配，提高數學學習效率，同時能幫助教師認識到學生的薄弱之處，進而有助于教師調整教學策略

三、影響中學生運算能力的因素

要想提升學生的數學運算能力，教師需要了解影響學生運算能力的因素筆者在實習期間通過批改作業和訪談將影響學生運算能力的因素分為以下三類

(一)概念、公式記憶模糊

部分學生在學習時對知識點的記憶模糊，記不住知識點，就會在運算時出現錯誤部分學生在學習的時候直接記住概念的名稱和符號，而沒有弄清楚概念的細節及其適用范圍由此可見，學生只有真正地理解概念，弄清楚概念之間的關聯，再加以練習，才能熟練掌握概念有些學生只是記住了公式中字母與字母之間的關系，而不注重公式的推導過程，因此不能理解公式的各種變形

(二)運算習慣不好

運算習慣不好包括以下兩個方面：一方面是審題馬虎看錯題目中的數字或符號是中學生在運算中經常出現的錯誤有近一半的學生在數學考試中會因為粗心大意而丟分另一方面是草稿紙的使用方式不恰當部分學生沒有固定的草稿紙，經常在書上、桌子上或試卷上進行運算，這樣就存在一些客觀因素，如桌子上的劃痕、書上原本的字體，學生在運算的過程中容易看錯數字，從而導致運算錯誤有些學生雖然有草稿紙，但是在草稿紙上字跡潦草，在驗算的時候會存在困難

(三)運算方法不熟悉

運算方法是指在面對復雜的習題時，學生會根據題目中給出的條件，選擇合適的方法進行計算，如換元法、整體迭代法、設而不求法等部分學生表示不能靈活運用特定的運算方法，自己獨自做題的時候不能想到合適的方法，需要別人提醒才能想到這表明學生對這些特定的運算方法只是了解，卻不夠深入，所以要別人提醒才會用教師總結運算方法，或者幫助學生掌握運算的技巧會使學生在解決數學問題時化繁為簡，反之，則會將簡單的問題復雜化

四、培養數學運算能力的策略

隨著我國教育工作者的努力和創新，新課程改革已經啟動，高中數學課程標準不斷發展，而數學運算能力的地位仍然重要因此，教師更應該緊跟新課標的指示，把數學運算能力的培養放到教學目標中去，并在教學過程中有效落實

(一)教師角度

首先，教師要重視對基本概念的教學學生進行數學運算的基礎就是數學概念，如果沒有掌握好這些基礎概念，學生在進行數學運算的時候就會不知所措因此，第一次引入新概念的課堂十分重要，教師可以要提前做好充分的準備在教學的過程中，教師要時刻關注學生的行為舉止，要讓學生耳目一新，給學生留下深刻的印象，再逐步深入，讓學生記住并理解新的知識其次，教師在教學的過程中要注意培養學生養成良好的運算習慣教師只有開始重視運算習慣，在課堂上多強調運算習慣的重要性并且板書規范的運算過程，才能讓學生潛移默化地意識到運算習慣對數學運算的重要性最后，教師要引導學生學會歸納運算規律，總結特定的運算方法例如，在教學數列的基本知識之后，教師可以抽取一節習題課來歸納常見的運算方法，將求解數列的通項公式和數列的前項和常用方法歸納起來對于每種方法，教師可以給出兩個例題，讓學生先自己求解，再在黑板上板書具體的步驟，給出習題，請學生上來板書，或者當作課后作業有了教師歸納的運算方法，學生再碰到不會的數列問題，翻開筆記溫習一下就好了

(二)學生角度

首先，學生要熟記各種基礎概念學生應該對基本的運算規則、公式定義熟記于心，避免在做題或考試的時候把公式記錯或記混淆而導致運算錯誤這里的熟記規則并不是要呆板地記住，而是在理解的基礎上加強記憶，在遇到不同的問題條件下可以靈活運用對于那些難記、易混淆的規則，學生可以采取重點記憶、搭配記憶、聯想記憶等方法其次，學生要養成好的運算習慣學生在審題時一定要仔細，可以將題目多讀兩遍，不要急著動手做題，要先讀懂題意在草稿紙上運算時，學生的字跡要工整一些，便于檢查和驗算最后，學生要歸納與總結運算方法許多學生的運算能力欠佳，這是因為缺乏總結與反思，對于錯題，看一眼答案，就覺得明白了，下次遇見一樣的題還是不會做因此，學生應該學會歸納與總結，因為只有徹底搞清楚自己在哪里出錯，才會在下次做題的時候避免這種錯誤學生可以準備一個錯題本，將自己做過的錯題按不同類型、不同錯誤原因或錯誤的頻次整理在一起，在復習的時候可以再拿出來寫一遍雖然很多學生明白歸納與總結的重要性，但是不能拿出一點點時間將其落到實處學生只有將歸納與總結落到實處，才能有效地提高自身的數學運算能力

五、結 語

數學運算能力作為學生學習數學的重要技能之一，并不是一朝一夕可以提升的教師在日常教學的過程中要重視數學運算，具體表現在重視對基本概念的教學，重視培養學生的運算習慣，重視引導學生總結運算規律和方法學生在學習的過程中要熟記并理解基礎概念和基本的運算規則，養成良好的運算習慣，歸納好錯題集總而言之，數學運算能力的提升需要教師和學生的共同努力