SWAT模型在天山林區林冠截留過程中的改進應用

董力軒, 常順利,*, 張毓濤

1 新疆大學資源與環境科學學院綠洲生態教育部重點實驗室,烏魯木齊 830046 2 新疆林科院森林生態研究所,烏魯木齊 830063

在森林生態系統中,降水量被分為林冠截留量、穿透降雨量和樹干莖流量三部分,其中林冠截留量在該系統的水文循環和水量平衡中占有重要地位,約占降水量的20%—40%[1—3]。因此,在應用SWAT模型[4—5]模擬森林生態水文過程時,林冠截留對地表徑流的影響不可忽視。

對林冠截留水文過程的模型化主要可以分為三類,即經驗模型、半理論模型和理論模型[6—8]。雖然經驗模型可以根據實測數據運用統計學方法直接推求林冠截留量和降雨量之間線性或非線性關系,但不能刻畫水文物理過程。因運算繁瑣,不易求解,如結合光線與林冠分配降雨規律形成的理論模型在實例中運行困難[6]。以Gash模型為代表的半理論模型相較于前兩者工作量小,參數易確定且運算求解方便,顯現了一定的優勢[9]。Gash模型的適用性較強,能夠廣泛使用在不同氣候類型或林分類型的研究中,如海洋性氣候森林[9],熱帶與亞熱帶森林[10]、干旱半干旱區灌木林[11]、地中海氣候森林等[12]。在國內,Gash模型應用在大興安嶺地區落葉松林[13]、熱帶季雨林[14]、華北油松人工林[15]、貢嘎山暗針葉林[16]和黃土區人工刺槐林[17]等區域并獲得了比較合理的模擬效果。SWAT模型與Gash模型在計算平均蒸發速率時都選擇了Penman-Monteith公式,這為兩種模型的耦合提供了便利條件[4, 9]。因此,將林冠截留的物理過程引入SWAT模型的流域模擬中意義重大。

本文以天山北坡中段雪嶺云杉(Piceaschrenkiana)林為研究對象,結合氣象觀測、林下穿透雨實測數據和野外調查獲得模型所需參數進行建模。考慮到研究區潛在蒸發遠遠大于實際蒸發[18],林冠截留作用明顯,符合Gash模型對每次降雨事件發生時初始條件的要求,進行基于物理過程的林冠截留模擬可以提高模型精度,為水資源管理提供更可靠的依據。

1 研究區概況

研究區位于烏魯木齊縣境內的烏魯木齊河流域(86°45′—87°56′E,43°00′—44°07′N),山區流域面積1070 km2,屬于中型流域,見圖1。河源位于天山烏魯木齊河源1號冰川,自南流向東北,出山口位于英雄橋。根據世界土壤數據庫(Harmonized World Soil Database,HWSD),土壤類型有簡育灰色土、鈣積黑鈣土、粘化栗鈣土、簡育栗鈣土、粘化鈣積土、永凍薄層土、松軟薄層土和冰川。研究區屬于溫帶大陸性氣候[18],春秋短暫,夏季晝夜溫差大,冬季漫長且多雪。日照時間長且日照輻射大,年平均氣溫為2—3℃,極端最高氣溫30℃(7月),極端最低氣溫-38℃(1月)。降水量少,年降水量400—600 mm,年內降水多集中在6—8月；蒸發量大,年蒸發量980—1150 mm[19]；年均相對濕度64%—66%;干燥度1.2—1.6。該區域植被類型是以雪嶺云杉純林為主的溫帶針葉林,占流域面積的10%左右,研究區內云杉分布廣泛且林冠截留作用明顯,流域特征符合研究需求,見圖1。

2 研究方法

2.1 模型的輸入數據

2.1.1氣象數據

選擇研究流域范圍內的大西溝、英雄橋和小渠子三站1993—2012的日降水、日最高溫、日最低溫、平均風速等氣象數據構建天氣發生器,整理后輸入氣象數據庫。

2.1.2數字高程數據

由地理空間數據云http://www.gscloud.cn/下載研究區DEM數字高程數據,選擇30 m 分辨率數字高程數據并且轉為WGS_1984_UTM_Zone_45N地理投影(圖1)。

2.1.3土地利用數據

選擇對地物分類更好的哨兵數據,經最大似然分類法得到精度為10 m的土地利用數據(圖1)。

2.1.4土壤數據

本研究采用世界土壤數據庫,裁剪出研究區,根據SAWT內置土壤類型進行重分類和重采樣處理以滿足模型的精度要求,使用SPAW軟件計算建模所需參數建立土壤數據庫。

2.1.5林冠截留觀測區布設

依托天山森林生態系統定位站于2010年7—8月設立林冠截留觀測區(東經87°27′,北緯43°25′)。該觀測區內主要植被為雪嶺云杉,無灌木分布。在林間空地布設自記數字雨量儀測定總降水量和降雨強度,在林下設置接雨蓬鏈接集水桶收集穿透雨量后換算為降雨量深度(mm),具體數據見表1。

表1 林冠層對降雨的分配

圖1 烏魯木齊河流域示意圖Fig.1 Sketch map of Urumqi River basin

2.2 SWAT林冠截留模型

當使用SCS曲線法計算地表徑流時,不會對林冠截留進行具體物理過程的模擬,估計為產流前地表蓄水量和入滲量的20%。當使用Green & Ampt入滲方程計算地表徑流和入滲時,必須額外計算林冠截留量[20]。SWAT允許林冠截留的最大水量每天在變化,該方法根據葉面積指數函數來計算其值。公式如下：

(1)

式中,canday為當日林冠截留的最大水量(mm),canmx為樹冠充分發育時的林冠截留量(mm),該參數需要使用者手動輸入。LAI為該植被當日的葉面積指數,LAImx為該植被的最大葉面積指數。

在SWAT模型中,得到給定日的降雨數據,模型會通過降雨量的大小來判斷是否會有穿透雨形成。公式如下：

(2)

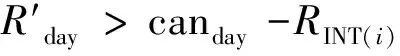
(3)

2.3 Gash模型

Gash模型描述的是一系列彼此分離的降雨事件,每個降雨事件都包含林冠加濕、林冠飽和、以及降雨停止后林冠干燥的過程,且假定每次降雨事件之間有足夠的時間讓林冠完全恢復到降雨前的干燥程度[9, 21]。模型將整個林冠在降雨過程中各個階段的截留損失相加得到總的林冠截留量。因為SWAT模型對于林冠截留的計算采用了單次降雨事件單獨計算的模式,并且根據降雨量的大小分為林冠截留量未飽和與林冠截留量飽和兩種情況,故將Gash模型拆解為分段函數以更好的與SWAT模型擬合。單一降雨事件發生時公式如下：

(4)

(5)

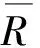
(6)

式中,S為林冠枝葉持水能力(mm)。

2.4 Gash模型參數的確定

圖2 降雨量與穿透雨量的回歸關系Fig.2 The relationship between throughfall and precipitation

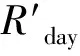
自由穿透雨系數p,為林內測得的平均可見天空率[23],經過野外實地調查郁閉度后確定為0.2。

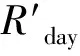
2.5 對SWAT模型子程序的修改

2.6 模型校準和驗證

模型的校準和驗證均在英雄橋出水口進行,本文通過決定系數R2、效率系數NSE、相對偏差系數PBIAS和均方根誤差RMSD來對模擬值和實測值的擬合度做出評價。決定系數R2的表達式[25]為：

(7)

Nash-Sutcliffe模型效率系數(NSE)的表達式[26]為：

(8)

偏差系數(PBIAS)的表達式為：

(9)

均方根誤差(RMSD)的表達式為：

(10)

標準差與皮爾遜相關系數的表達式為：

(11)

(12)

(13)

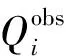
2.7 不確定性分析

SWAT模擬的流量不確定性主要是由于輸入數據的偏差,建模者的專業知識不足或改進模型的結構不合理等原因導致。本文中使用了分位數回歸方法,通過計算不同分位數的條件分布來進行非參數不確定性分析[27—29]。確定置信區間后,使用P因子和R因子來量化不確定性。P因子代表了95%的預測不確定性(95PPU),是落在95PPU范圍內數據的數量與總數據數量的比值。評價校準質量的另一個參數是R因子,表示95PPU范圍的平均寬度與觀測數據的標準差的比值。在理想情況下,P因子的取值在0—100%之間,R因子介于0—∞,當R<1.5時認為可接受,在P因子為1且R因子為0是模擬值與觀測值完全一致。

3 結果與分析

3.1 參數的敏感性分析

SWAT模型和SWAT-Gash模型均使用SWAT-CUP內SUFI- 2算法進行模擬值的敏感性分析。首先根據類似研究區常用的25個參數[30—31]對SWAT模型進行1000次模擬,發現其中13個參數對SWAT模型模擬結果影響明顯(表2),再將其進行500次迭代得到最優校準。同理,對SWAT-Gash模型進行參數的敏感性分析后選擇以下16個參數。經分析發現兩種模型均對SCS徑流曲線系數、土壤飽和水力傳導系數、土壤可利用有效水、淺層含水層水位、融雪基溫和平均坡長等參數體現出更高的敏感性。

3.2 SWAT模型與SWAT-Gash模型在徑流模擬中的性能對比

考慮到氣象數據的年際變化,設置1993—1996年為模型的預熱期,以減少由于氣象數據而導致的潛在不確定性。1997—2004為校準期,2005—2012為驗證期。如圖3和圖4是SWAT模型與SWAT-Gash模型在校準期和驗證期的徑流模擬過程線,SWAT-Gash模型的模擬值優于SWAT模型的模擬值,體現在SWAT-Gash模型更好的重現了高流量與低流量,SWAT模型會低估高流量。在校準期與驗證期,SWAT-Gash模型與SWAT模型在出山口位置的月平均徑流量分別為8.45—8.50 m3/s和6.55—6.86 m3/s之間;NSE值分別在0.63—0.85和0.58—0.82之間；R2值分別在0.65—0.86和0.59—0.83之間；PBIAS值分別在9.7%—11.5%和9.2%—17.1%之間(表3)；表明在該研究區SWAT-Gash模型的適用性高于SWAT模型。

校準期和驗證期兩種模型的均方根誤差(RMSD)、標準差(SD)和相關系數等均在泰勒圖中體現(圖5)。圖中各點與x軸上實測值點之間的徑向距離表示RMSD的大小,反映了各模型的模擬能力。SWAT-Gash模型得出的RMSD更低,在校準期和驗證期的值分別為3.22 m3/s和4.68 m3/s。使用SWAT模型時,RMSD值分別為3.49和7.80 m3/s,說明與SWAT-Gash模型相比SWAT模型在干旱半干旱區的徑流模擬效果欠佳。各點到原點之間的距離表示各組模擬值與觀測值的標準差。在校準期SWAT模型和SWAT-Gash模型的標準差分別為7.59和7.33,驗證期標準差分別為6.45和6.54。SWAT-Gash模型在驗證期標準差較大,可能是因為敏

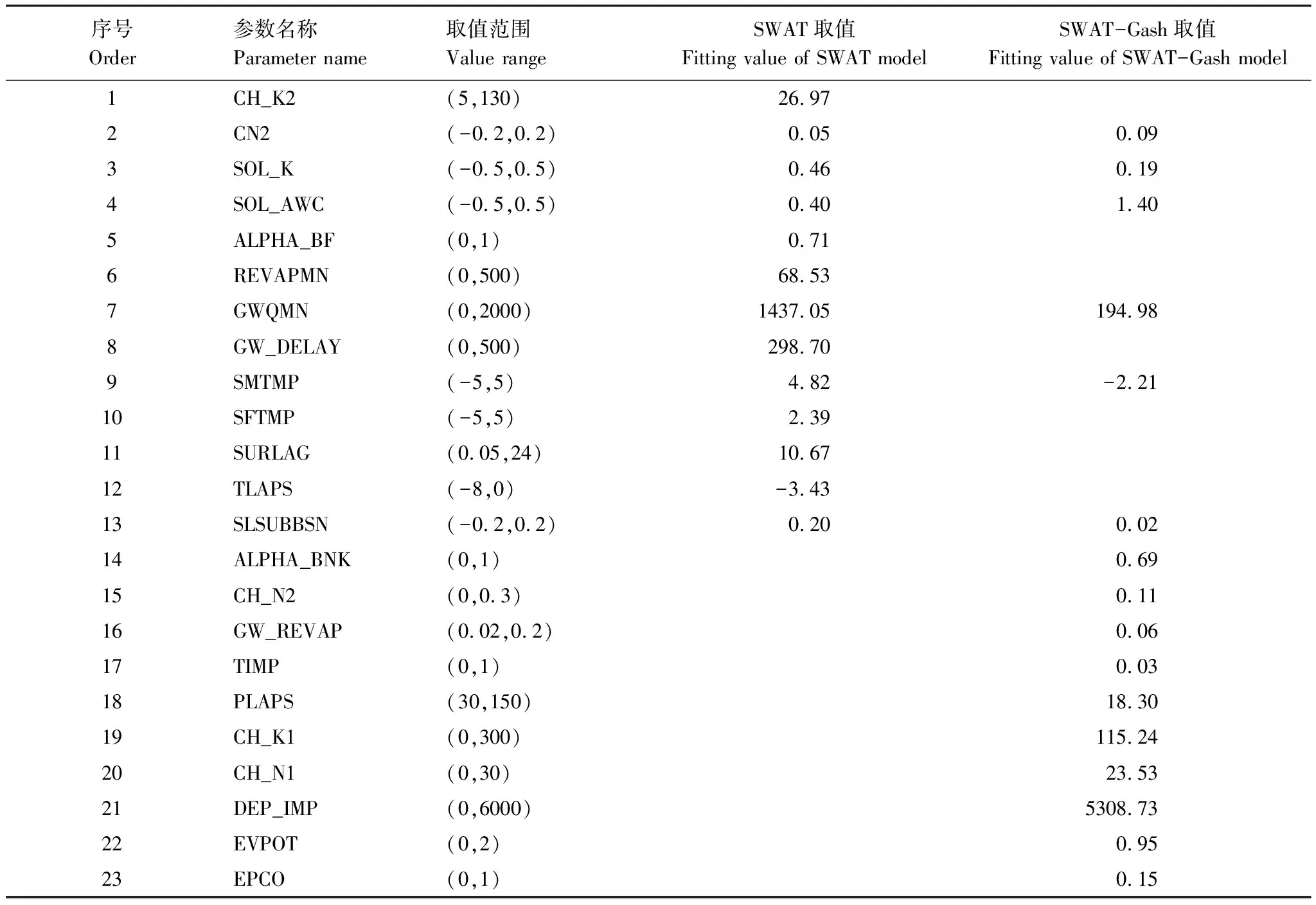
表2 SWAT模型與SWAT-Gash模型敏感性參數

SWAT：水土評估工具 Soil and water assessment tool;CH_K2：主河道有效滲透系數 Effective hydraulic conductivity in main channel;CN2：徑流曲線數 Curve number of moisture condition Ⅱ;SOL_K：飽和滲透系數 Hydraulic conductivity of the soil;SOL_AWC：土壤有效含水率 Available water capacity of soil layer;ALPHA_BF：基流α因子 Baseflow alpha factor;REVAPMN：發生再蒸發的淺層含水層水位閾值 Threshold depth of water in the shallow aquifer to “revap” to occur;GWQMN：發生回歸流的淺層含水層水位閾值 Threshold depth of water in the shallow aquifer required for return flow to occur;GW_DELAY：地下水時間延遲 Groundwater delay;SMTMP：融雪基溫 Snow melt base temperature;SFTMP：降雪基溫 Snowfall temperature;SURLAG：地表徑流滯后系數 Surface runoff lag time;TLAPS：氣溫垂直變率 Temperature laps rate;SLSUBBSN：平均坡長 Average slope length; ALPHA_BNK：河岸調蓄基流α因子 Baseflow alpha factor for blank storage;CH_N2：主河道曼寧系數 Manning′s "n" value for the main channel;GW_REVAP：地下水再蒸發系數 Groundwater “revap” coefficient;TIMP：積雪溫度滯后因子 Snow pack temperature lag factor;PLAPS：降水垂直變率 Precipitation laps rate;CH_K1：支流有效滲透系數 Effective hydraulic conductivity in tributary channel alluvium;CH_N1：支流曼寧系數 Manning′s "n" value for the tributary channels;DEP_IMP：土壤不透水層深度 Depth to impervious layer in soil profile;EVPOT：壺穴政法系數 pothole evaporation coefficient；EPCO：植物吸收補償因子 Plant uptake compensation factor

表3 模型徑流模擬評價指標

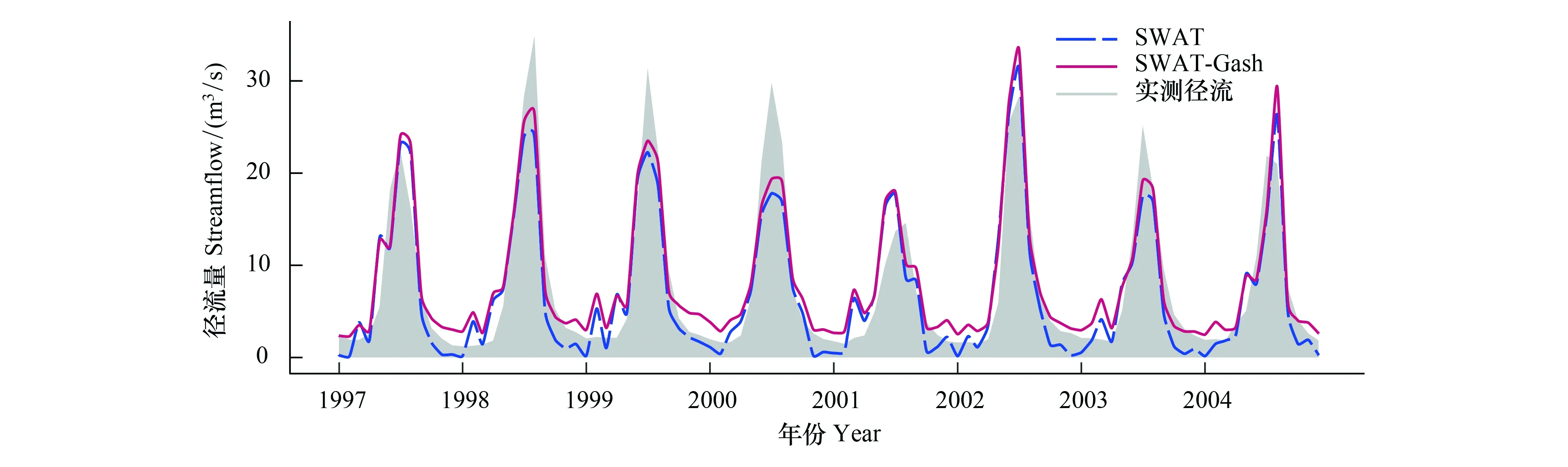
圖3 SWAT模型與SWAT-Gash模型校準期徑流模擬預測對比Fig.3 Comparison of runoff simulation prediction between SWAT model and SWAT gash model in calibration period

圖4 SWAT模型與SWAT-Gash模型驗證期徑流模擬預測對比Fig.4 Comparison of runoff simulation prediction between SWAT model and SWAT gash model in validation period

感性參數更多,但總體上該模型仍有更好的表現。相關系數表示出山口實測徑流數據和模型模擬值之間的關系,表明地表徑流在時間序列上的相似性。SWAT-Gash模型在校準期與驗證期的相關系數分別為0.93和0.81,高于SWAT模型的0.91和0.77。相較于SWAT模型,改進模型在校準期和驗證期模擬高流量的能力更加突出。

圖5 SWAT模型和SWAT-Gash模型在校準期和驗證期的泰勒圖Fig.5 Taylor diagram of calibration period and validation period for SWAT model and SWAT-Gash model

3.3 基于分位數回歸的不確定性分析

本文中定義了95%的置信區間β∈[0.025,0.975],使用兩種模型的驗證期徑流量與觀測流量進行基于分位數回歸的不確定性分析。如圖6所示,在驗證期SWAT模型的95%置信區間的平均厚度為13.50 m3/s,SWAT-Gash模型為12.86 m3/s,表明SWAT-Gash模型在本研究區的模擬表現更佳。SWAT-Gash模型的P因子為0.96,即96%的觀測值可以被該模型95%置信區間所包括,略高于SWAT模型(0.93)。此外,SWAT-Gash模型的R因子(1.19)低于SWAT模型(1.26),表明前者的不確定度范圍相對更窄。

圖6 SWAT模型和SWAT-Gash模型月徑流模擬的不確定性分布Fig.6 Uncertainty distribution of SWAT model and SWAT-Gash model in monthly runoff simulation

4 討論與結論

4.1 SWAT模型與SWAT-Gash模型在烏魯木齊河流域的應用

本文將Gash林冠截留模型與SWAT模型耦合后的模擬結果與原始SWAT模型的模擬結果進行對比分析,經過校準和驗證后發現SWAT模型與SWAT-Gash模型在該流域的應用均取得了較好的效果,該結論與前人在烏魯木齊河流域的建模結果一致[30—32],但SWAT-Gash模型表現出更高的模擬精度。當使用SWAT模型在烏魯木齊河流域模擬時,校準期徑流重現表現較好,驗證期表現不佳,造成這種現象的原因可能是模型結構復雜,敏感性參數對模擬結果的影響較大[33—35]。該流域內坡面匯流過程、地下水與河道的補給排泄過程和融雪過程[36—37]是影響山區地表徑流的主要因素,僅通過調整描述水文過程的參數無法進一步提升模型在該區域的適用性。與SWAT模型相比,SWAT-Gash模型會高估該流域的低流量,Gash模型輸入數據的誤差也會影響SWAT-Gash模型地表徑流的預測。Gash模型計算時要求參數較多,雖然這些參數的確定方法經過國內外前人研究的驗證[9,12,17,22—23],可以得到較好的結果,但王艷萍等人[17]研究表明本文方法得出的參數模擬值偏高。Gash模型與SWAT模型耦合時,對林冠截留物理過程的描述更加詳細,結合雪嶺云杉林下穿透雨實測數據得出滿足Gash模型的參數,使SWAT-Gash模型在該研究區的模擬表現更佳。

4.2 SWAT模型與SWAT-Gash模型的不確定性分析

本文采用了基于分位數的不確定性分析。與SWAT模型相比SWAT-Gash模型在基于分位數回歸的不確定性分析中的表現更佳,也表明Gash林冠截留模型對SWAT模型在烏魯木齊河流域的模擬改進效果明顯。通常在SWAT模型的建模中,將許多復雜水文過程用簡單的經驗系數進行參數化,增加了模型的不確定性[27]。而本研究提出的SWAT-Gash模型中,將林冠截留過程和最大冠層截留量參數替換為基于物理過程的方程,從而提高了模型的適用性。SWAT-Gash模型的改進方法可以提高天山北坡中段中小型流域的水文模擬精度,為該區域水資源管理提供更可靠的依據。此外,本研究的降雨量分配數據代表性有所欠缺,還需要在不同地形條件下收集時間尺度更長的降雨分配數據,使用更多樣的方法驗證Gash模型所需參數,從而在該流域進行更精細化的建模。

4.3 結論

Gash模型參數易于獲取,能夠通過降雨量、穿透雨量和林冠截留量等數據推求,可以較好的在天山林區進行林冠截留過程的模擬。本文基于SWAT模型,將Gash模型方程代替經驗公式提出新的SWAT-Gash模型。此方法可以提高烏魯木齊河流域水文模擬的精度。同時使用基于分位數的不確定分析發現改進后模型與出山口處實測地表徑流數據的相似性更高,適用性高于原始SWAT模型。