基于小波變換算法實現刀位點可控誤差預處理研究

袁雨禾，吳闖

（揚州大學機械工程學院，江蘇揚州，225127）

0 引言

數控加工中體現性能優劣的兩個主要指標：一是沿著加工面的加工路徑要求平整，而是沿著加工面的加工曲度要求平順[1,2]。這就需要刀位點采取有序性序列分布，使其具有高可靠性。并通過平順性處理使加工質量得到提升的同時降低加工成本[3,4]。

Douglas等[5]提出Split方法，達到了曲線平順性目的，然而較難處理曲線曲率較大情況。趙等[6]提出平順插補算法，實現了加工軌跡曲率的平順過渡，但算法復雜且難以控制誤差。S.Mallat等[7]提出多分辨分析概念，為小波變換函數的建立奠定了基石。Daubechies等[8]構造正交小波變換基函數，促進了小波變換分析系統理論初步構建。崔等[9]構造半正交小波變換基函數，促使小波變換系統理論得以完整表達。之后該理論被廣泛應用于圖像與信號處理，所具有的多尺度特性可用于刀位點平順處理。基于此，本研究首先通過小波變換算法對采集的刀位點三維信號進行修飾，隨后根據誤差閾值化策略重構刀位點三維信號，從而使刀位點軌跡曲線實現平順性變化。

1 刀位點的小波變換平順算法

如圖1所示，ks為理想軌跡，k0、k1、k2、k3為原始刀位點，為經小波變換平順后的刀位點，ε為可控誤差。刀位點x方向、y方向和z方向誤差可表示為：

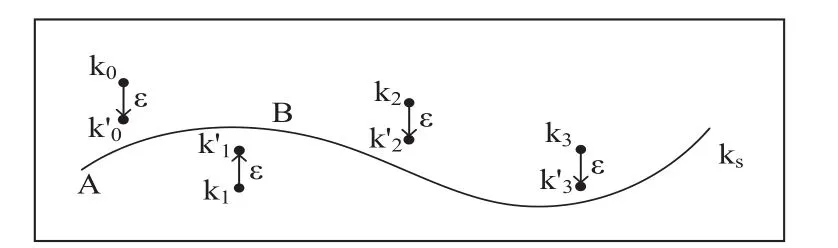
圖1 刀位點的小波變換

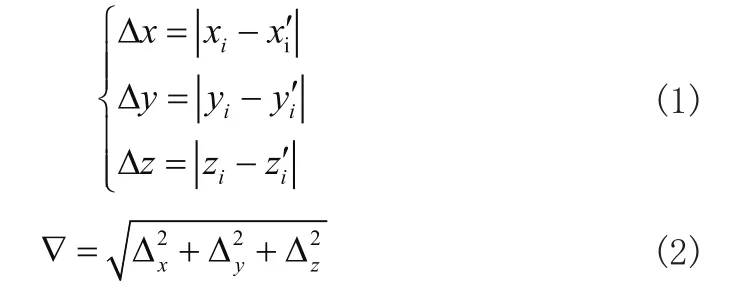
對刀位點的小波變換平順就是希望?在ε的范圍內盡可能的接近ks，設S為刀位點曲線，A為其上一點，動點P從A出發沿曲線前行，當到達曲線上另一點B時，形成弧長L，這時B點既可用直角坐標系(x,y,z)表示，又可用弧長L參數方程表示。

其參數方程可表示為：

由于每一L值唯一確定一個x，y，z，因此可得到三組有關li的函數，進而可用小波變換對此三組單調函數處理。設弧長L刀位點數為n+1，從點l0（x0,y0,z0)到點li(xi,yi,zi) 弧長為：

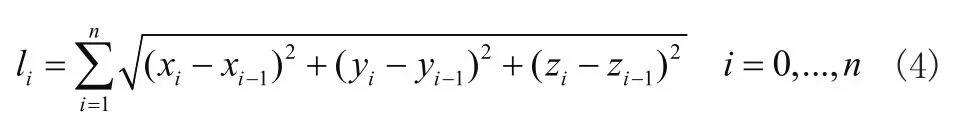
由于刀位點的離散性，而曲線S在離散點上取值，故弧長li也在離散點上對應取值，可得曲線S的三組點集{(li,xi),i= 0 ,...,n}，{(li,yi),i= 0 ,...,n}和{(li,zi),i= 0 ,...,n} 。用小波變換對各條曲線處理，即ki經小波變換后為ki′，在ε內實現對刀位點的平順處理。

2 刀位點的小波變換平順算法

3 仿真

采用MATLAB對刀位點進行仿真，選取76個刀位點作為小波變換的預處理對象。首先采用小波變換將選取的刀位點數據按照X/Y/Z方向分解為三組一維數據（如圖2所示）。其次采用Daubechies小波變換對信號進行兩層分解，并對高頻與低頻部分閾值化處理（如圖3所示），最后重構高低頻信號，由圖2和圖3可知，變換前后刀位點信號平順性顯著增加。

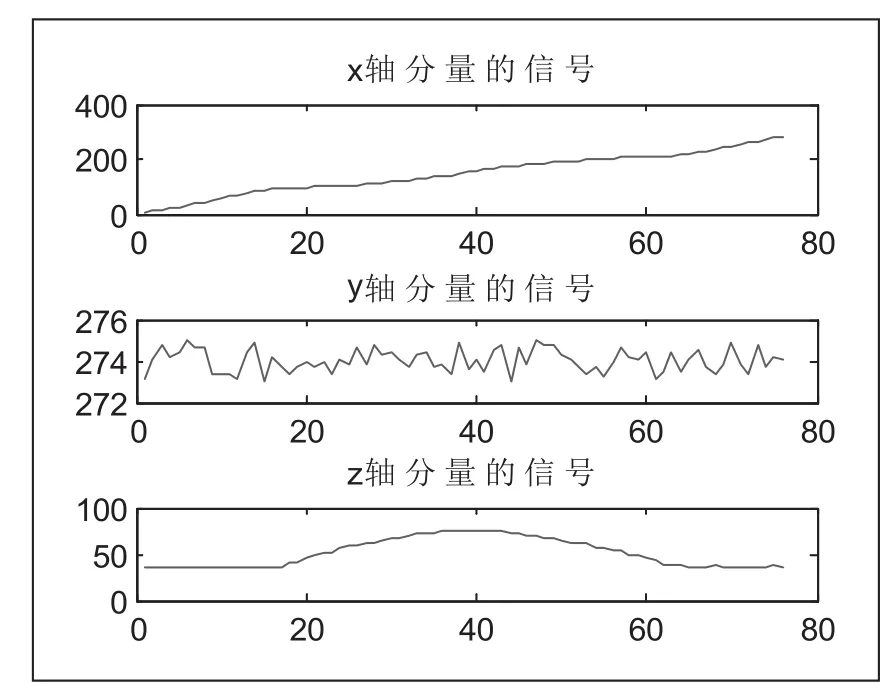
圖2 平順前分量信號

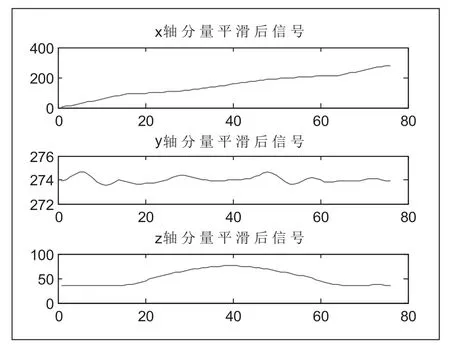
圖3 平順后分量信號

4 總結

物體加工表面的光順性是產品檔次的重要體現，而刀位點的平順性可使產品表現出光亮特征。本文通過研究小波變換的多尺度性質，提出了刀位點三維信號的小波變換平順算法，采用Daubechies小波變換對空間分解的X/Y/Z軸一維信號進行平順性修飾，并利用高頻系數作為低頻表示誤差的判斷方法實現了閾值可控誤差的擬合，之后將平順處理后的三組一維信號重構為刀位點的空間軌跡，實現了刀位點的平順性，最后通過MATLAB仿真分析驗證了該算法的有效性，為數控加工的三維軌跡平順性處理提供了理論支持。