常見雙層介質材料γ射線照射量累積因子的計算與分析

李 華，魏子洋，趙 原，劉立業，李 會，韋加富

(中國輻射防護研究院 核藥研發轉化與精準防護山西省重點實驗室，太原 030006)

點核積分方法是常規γ射線屏蔽設計與計算分析最常用的方法之一，廣泛應用于核設施輻射屏蔽與輻射劑量場的計算中。近年來，隨著計算機技術的飛速發展，核設施全周期中的數字化輻射防護技術已經成為目前輻射防護領域的研究熱點之一，其中點核積分方法在γ輻射場模擬中表現出優秀的計算效率和偏保守的計算結果，使其成為各個國家在數字化輻射防護模擬仿真軟件開發中的首選底層核心計算方法[1-5]。

累積因子是點核積分方法中考慮散射光子的物理量，是影響其計算結果準確性的主要因素。在過去的幾十年中，國外對累積因子開展了較多的研究[6-10]，在單一材料的累積因子計算中，美國標準化所(ANSI)于1991年發布了較為完備的累積因子數據庫[11]，雖然其已經遠超過了ANSI定期更新的時限，但目前仍是各點核積分計算軟件使用的主要底層數據庫。對于雙層及以上材料組合下累積因子數據的計算，主要圍繞對經驗近似公式展開研究[12-14]，目前雙層材料累積因子符合較好的是Lin和Jiang提出的經驗公式[12]，多層材料累積因子符合較好的是Suteau和Chiron提出的迭代計算方法[13]，然而這些經驗公式往往比較復雜并且需要較多其他基礎參數參與計算，使其在輻射防護相關計算中并不實用。國內目前使用的累積因子數據大部分都是引自20世紀70年代中國科學院工程力學研究所編著的《γ射線屏蔽參數手冊》[15]，雖然開展了一些常見單層材料累積因子的計算工作[16-17]，但尚未對雙層及以上材料組合下的累積因子計算進行細致的研究。

近年來，一方面可用于累積因子計算的代碼工具和基礎截面數據庫不斷地在更新迭代，另一方面雙層材料組合是核設施現場最為常見的屏蔽與輻射場計算情形，其累積因子數據是用于核設施現場點核積分模擬計算工具準確實用的關鍵所在。為此，本文基于Geant4模擬平臺，設計并開發了專門用于雙層材料累積因子的計算程序，利用球型介質組合模型分別計算并建立了核設施現場常見雙層材料組合的累積因子數據庫，將計算結果與可靠性較好的經驗公式模擬結果進行了對比分析，驗證了雙層材料累積因子數據計算結果的準確性。本文工作可為我國累積因子數據庫更新和改進點核積分計算程序等提供技術支持。

1 計算方法

1.1 計算模型

參考美國ANSI/ANS-6.4.3標準中計算單層材料累積因子的無限大球型介質模型，本文采用了近似無限大的球型雙層介質材料模型，如圖1所示。其中各向同性點源包含在內層介質中，統計測量點在外層介質中。考慮到程序的計算效率和無限大模型假設引入的偏保守量，程序計算時外層介質材料的厚度設置為近似無限大。與實際計算需求相比，本文提供的雙層介質材料的累積因子數據，大多情況下仍然偏于保守，因為通常現實中的材料尺寸并非無限大，測量點位都處于空氣當中。

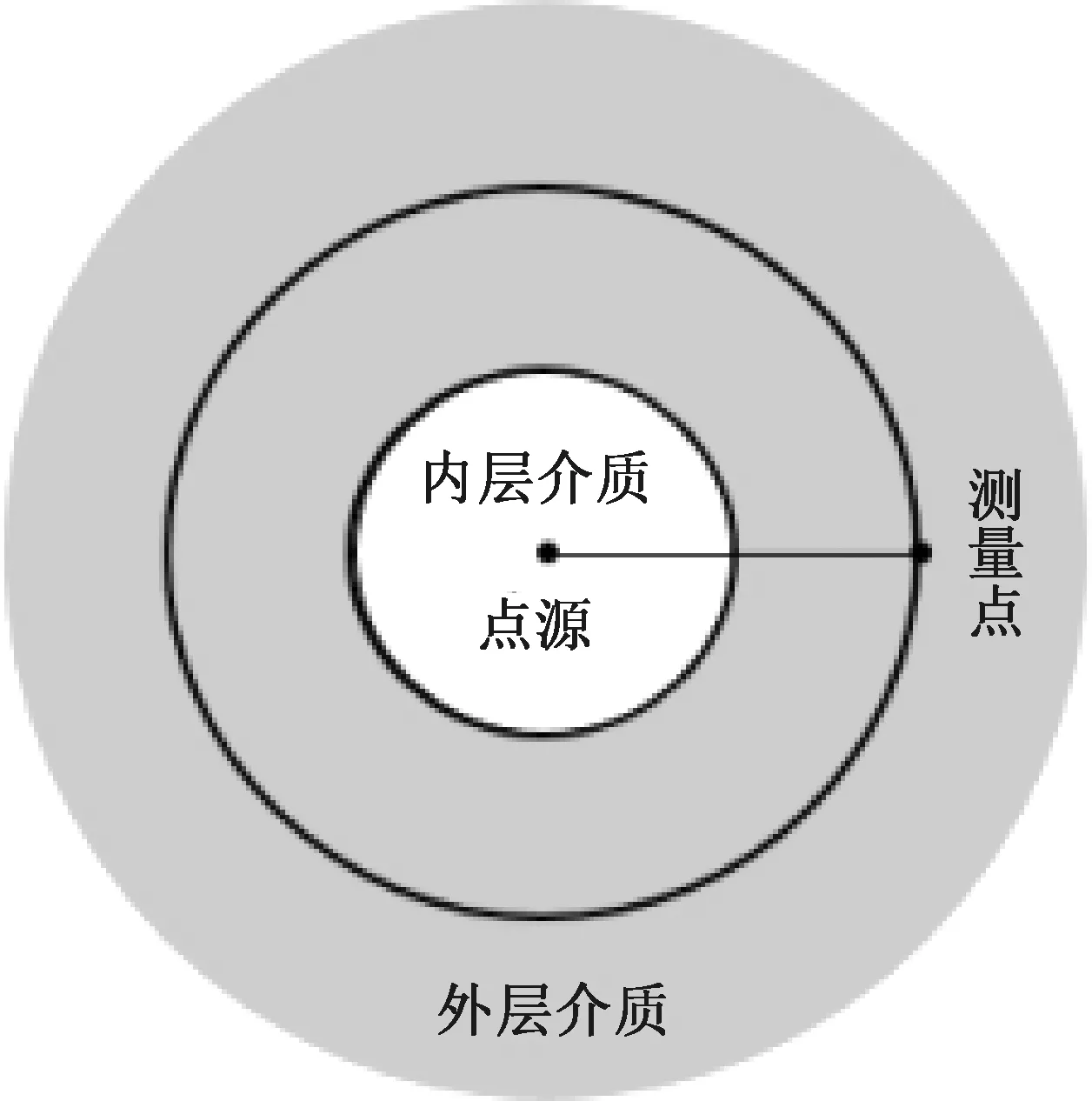
圖1 雙層介質材料累積因子計算模型

1.2 累積因子的計算

本文基于Geant4模擬平臺，設計并開發了專門用于雙層材料累積因子的計算程序，如圖2所示。計算所使用的版本為Geant4_10_3，采用了較新的截面數據庫G4EMLOW6.50，材料的質量衰減系數采用的是美國國家標準和技術研究院NIST(National Institute of Standards and Technology)發布的Standard Reference Database 126數據庫中的數據，物理過程考慮了軔致輻射和相干散射。

圖2 基于Geant4模擬平臺開發的雙層材料累積因子計算程序

程序在計算累積因子時，需要讀取每層介質材料的質量衰減系數(μ/ρ)，以及輸入第一層介質材料的厚度和第二層介質材料的厚度間隔、γ光子的能量，以及模擬的粒子數。結合統計面記錄的光子通量和程序內置的光子通量與照射量轉換系數，將最終給出雙層材料的照射量累積因子數據。同時，計算采用球型模型的優勢在于統計面的設置可根據第二層材料的厚度自由選取，一次模擬能夠批量得到相同能量和第一層材料厚度，第二層材料不同厚度下的累積因子數據。本文的計算數據，均采用了較大的模擬粒子數，確保統計漲落在5%以內。

1.3 雙層材料累積因子的經驗計算公式

在雙層介質累積因子計算領域，Lin和Jiang提出的經驗計算公式是相對符合較好的[12]，本文將Geant4模擬計算結果與經驗公式計算結果進行對比分析。該經驗公式的數學表達式如下所示[12]：

B(X1,X2)=B2(X2)+[B2(X1+X2)-

B2(X2)][K(X1)C(X2)]

(1)

式中，X1是第一層介質的光子平均自由程數(MFP)；X2是第二層介質的光子平均自由程數，(MFP)；B(X1,X2)是雙層材料組合下的累積因子；Bi(X)是第i層材料在X自由程厚度的累積因子；K(X1)=[B1(X1)-1]/[B2(X1)-1]，表示透過第一層材料X1自由程厚度的散射分量與透過第二層材料X1自由程厚度的散射分量之間的比值；C(X2)是校正因子，其建議的表達式如式(2)、式(3)所述。

對于高Z材料在前，低Z材料在后的情況，C(X2)的表達式為：

C(X2)=exp(-1.08βX2)+

1.13β·l(X2)

(2)

對于低Z材料在前，高Z材料在后的情況，C(X2)的表達式為：

C(X2)=0.8·l(X2)+

(γ/K)exp(-X2)

(3)

(4)

本文在利用Lin和Jiang經驗公式計算時，所使用的單層材料的累積因子數據，均是基于無限大模型由Geant4模擬計算得到。

2 計算結果與分析

2.1 常見雙層材料累積因子數據的計算與分析

基于上述理論，本文利用基于Geant4開發的雙層材料累積因子計算程序，分別對核設施現場常見的水、鐵、鉛和混凝土4種材料的12種兩兩組合下的照射量累積因子數據進行了計算，形成了常見雙層材料的累積因子數據庫。計算時參照了美國標準ANSI/ANS-6.4.3—1991將能量在0.015～15.0 MeV范圍內分為25個能量間隔，并考慮實際介質厚度將平均自由程(MFP)選為0.5、1.0、1.5、2.0、2.5。由于數據數量較大，文中僅給出部分材料組合下的累積因子數據結果進行分析。

2.1.1高Z材料在前、低Z材料在后的累積因子

以鉛和混凝土組合、鉛和水組合為例，將第一層介質材料鉛的厚度固定為1 MFP，第二層介質材料厚度分別選取0.5、1.0、1.5、2.0、2.5 MFP，照射量累積因子的計算結果分別如圖3和圖4所示。圖中為對數坐標，L表示鉛材料，C表示混凝土材料，W表示水材料，“1.0L+0.5C” 表示第一層為1 MFP厚度鉛和第二層為0.5 MFP厚度混凝土的材料組合，以此類推，余圖同。

L—鉛材料；C—混凝土材料。

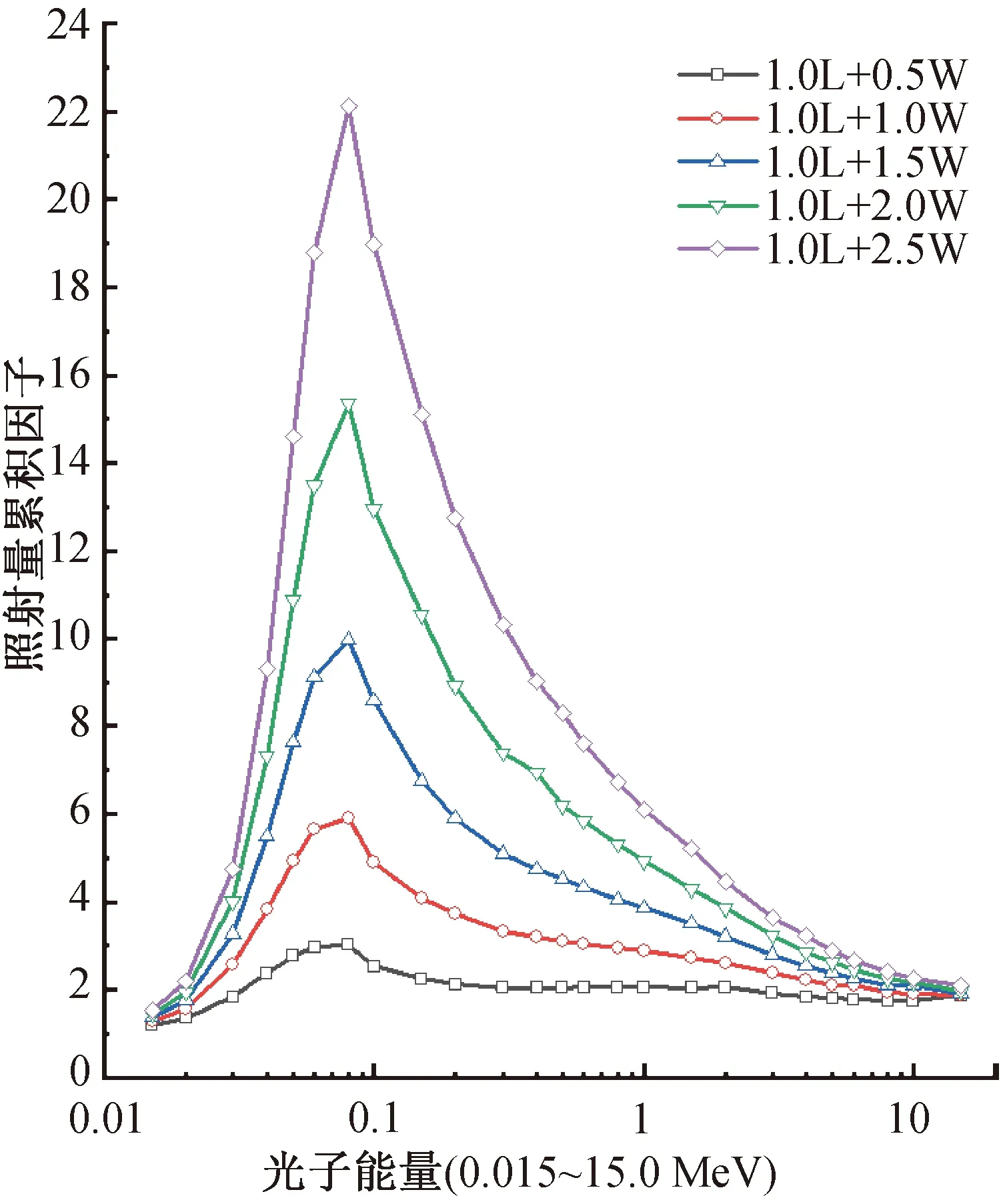
L—鉛材料；W—水材料。

從圖3和圖4中可以看出：無論是鉛和混凝土組合，還是鉛和水組合，在第二層材料不同厚度下照射量累積因子隨光子能量的增大均表現為先增大后減小；對于鉛和混凝土組合，累積因子的峰值在混凝土厚度較薄時(0.5或1 MFP)，出現在0.09 MFP能量附近，在混凝土厚度增大時(2或2.5 MeV)累積因子的峰值逐漸出現在0.15 MeV能量附近；對于鉛和水組合，隨著水的厚度增加，累積因子的峰值一直出現在0.09 MeV能量附近。

這是因為根據γ射線與物質的相互作用關系可知：在低能段時，光電效應占主導優勢；在中能段時，康普頓散射占主導優勢；在高能段時，電子對效應占主導優勢。因此作為描述光子康普頓散射物理量的累積因子，會出現隨著光子能量先增大后減小的變化趨勢。對于鉛材料，其對于γ射線的線衰減系數在0.09 MeV能量附近存在峰值，同時對于單層介質而言[16]：鉛的累積因子數據在0.09 MeV能量附近出現峰值；混凝土的累積因子數據在0.15 MeV能量附近出現峰值；水的累積因子數據在0.1 MeV能量附近出現峰值。因此，對于鉛和混凝土組合，在混凝土厚度較薄時，鉛對于光子的散射起主導作用，就會導致累積因子的峰值出現在0.09 MeV能量附近；在混凝土厚度增大時，其對光子的散射逐漸起主導作用，導致累積因子的峰值逐漸出現在0.15 MeV能量附近。對于鉛和水組合，原因類似。

2.1.2低Z材料在前、高Z材料在后的累積因子

以水和混凝土組合、水和鐵組合為例，同樣將第一層介質材料水的厚度固定為1 MFP，第二層介質材料厚度分別選取0.5、1.0、1.5、2.0、2.5 MFP，照射量累積因子的計算結果分別如圖5和圖6所示。其中I表示鐵材料。

W—水材料；C—混凝土材料。

從圖5和圖6中可以看出，無論是水和混凝土組合，還是水和鐵組合，累積因子值的變化情況均存在一個能量分界點Eth。當光子能量小于分界點Eth時，照射量累積因子值會隨著第二層介質材料厚度的增大而減小；當光子能量大于分界點Eth時，照射量累積因子值則會隨著第二層介質材料厚度的增大而增大。

這是因為當光子能量大于分界點Eth時，康普頓散射占主導優勢，隨著第二層介質材料厚度的增加，光子在通過介質材料時發生康普頓散射的概率會增大，因此照射量累積因子值增大；當光子能量小于分界點Eth時，光電效應占主導優勢，隨著第二層介質材料厚度的增加，雖然光子發生康普頓散射的概率在增大，但同時光子發生光電效應而被吸收的概率也在增大，且增幅比康普頓散射的概率增幅大，綜合作用下導致第二層介質材料厚度增加時會引起更多的光子被吸收，從而使得照射量累積因子減小。圖6中在能量分界點左側也出現了峰值，是鐵材料的線衰減系數在該能量區間存在峰值和Geant4統計偏差共同作用的結果；能量分界點右側的峰值對應光子在雙層介質材料下的康普頓散射概率最大。

2.1.3雙層材料與單層材料的累積因子數據對比

為了進一步對比分析不同組合順序的雙層介質材料與單層介質材料下的累積因子數據結果，本文參考Lin和Jiang文獻[12]，選取光子能量為0.5和1.0 MeV，以及計算中常見的水和鐵兩種材料，不同組合形式下的累積因子數據對比結果,如圖7和圖8所示。其中單層材料水或鐵的厚度變化范圍為0～8 MFP；雙層介質材料組合的第一層厚度固定為3 MFP，第二層厚度變化范圍為0～5 MFP。記EWI、EIW、EW和EI分別是水鐵材料組合、鐵水材料組合、單層水材料、單層鐵材料下的累積因子。

W—水材料；I—鐵材料。

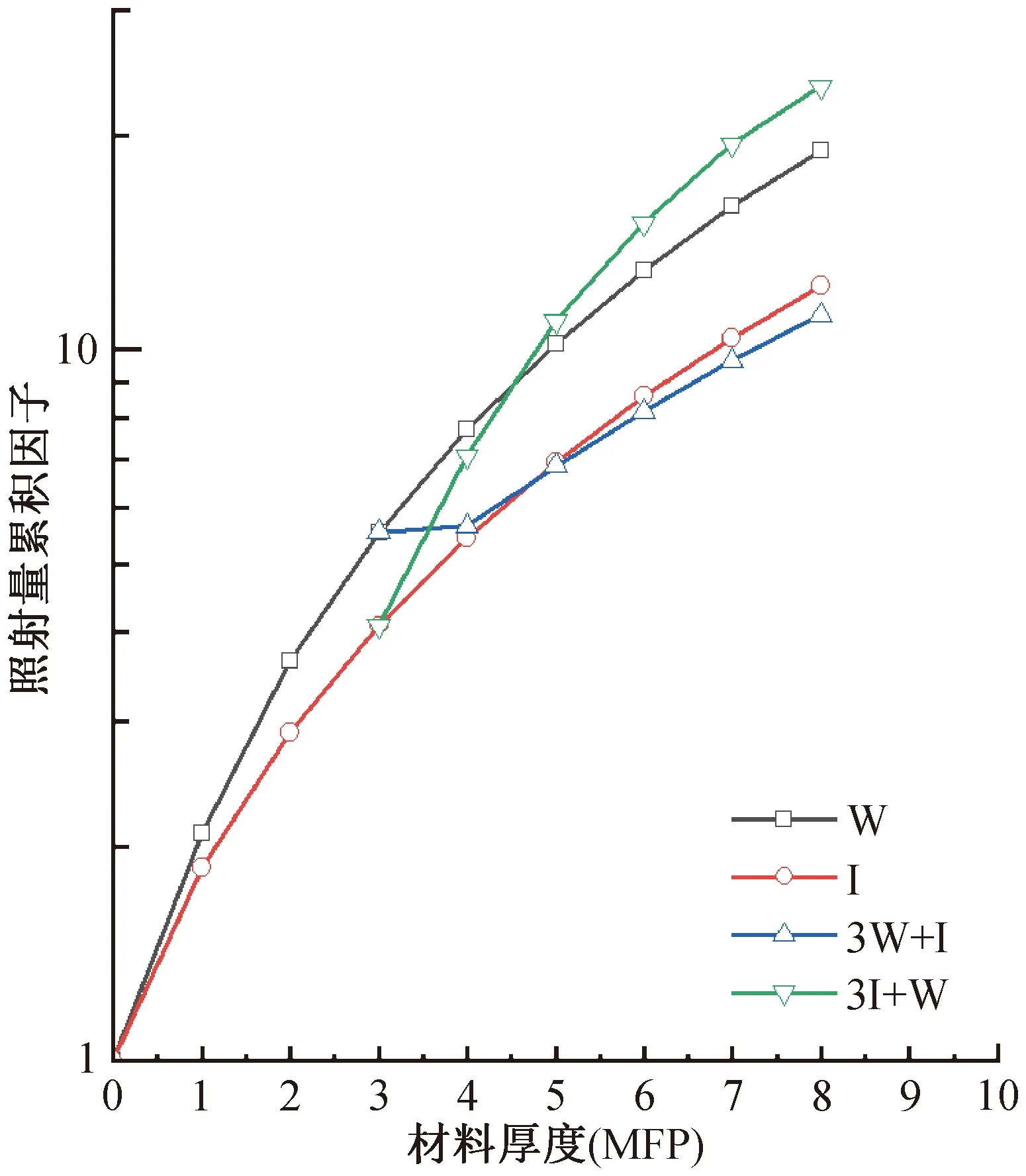
W—水材料；I—鐵材料。

從圖7和圖8中可以看出：光子能量為0.5或1.0 MeV，當介質材料總厚度大于4 MFP時，EIW始終大于EWI；并且隨著總介質厚度的進一步增大，相同總厚度下的累積因子表現出EIW>EW>EI>EWI的變化趨勢。

2.2 與經驗公式計算結果的對比分析

為了進一步驗證本文基于Geant4模擬雙層介質材料照射量累積因子數據的可靠性，對比分析了部分雙層材料組合下，γ光子在1.0 MeV能量時照射量累積因子的經驗公式和Geant4模擬計算結果列于表1。其中經驗公式來自Lin和Jiang文獻[12]，且公式中采用的單層介質材料累積因子數據是通過Geant4模擬得到的。

表1 基于不同計算方法的部分雙層材料組合的照射量累積因子數據對比

從表1中數據可以看出，本文基于Geant4計算的雙層介質材料累積因子數據與Lin和Jiang經驗公式的計算結果，大多數相對吻合較好，一定程度上驗證了本文數據計算結果的可靠性。鐵水材料組合下兩者的偏差基本約為5%，鉛水材料組合下兩者的偏差相對較大，約為10%～16%。這是因為經驗公式為了達到普適性，并沒有很好地考慮諸如鉛介質材料衰減系數存在峰值等特殊情況，同時本文在利用Geant4計算累積因子時，采用了較新的底層截面數據庫和線衰減系數庫，以及存在統計漲落等綜合因素。

3 結論

本文使用Geant4開源程序包設計開發了用于雙層介質材料的累積因子計算程序，并對核設施現場常見的水、鐵、鉛和混凝土4種材料的12種兩兩組合下的照射量累積因子數據進行了計算，形成了相應的雙層材料照射量累積因子數據庫。同時將部分計算數據與可靠性較好的經驗公式模擬結果進行了對比分析，結果表明它們之間相對吻合較好，偏差大多數在10%以內，一定程度上驗證了本文累積因子數據計算結果的準確性。

目前尚未發現公開發布的雙層及多層累積因子相關數據庫，Lin和Jiang文獻也只是針對部分能量與材料組合進行了計算，并不包括γ光子全能量段以及多種材料組合等情況。雖然其經驗公式的部分計算結果相對較好地符合蒙特卡羅模擬數據，但由于其復雜程度以及需要較多不易獲取的基礎參數(如μc/ρ等)，使其在實際使用中仍存在一定的困難。本文使用Geant4計算并建立的常見雙層材料組合下的照射量累積因子數據庫，可以方便快捷地為γ輻射場模擬仿真與輻射屏蔽計算提供基礎數據。