三次型蔡氏電路的設計及應用*
呂恩勝
(河南應用技術職業學院機電工程學院,河南 鄭州 450042)
Chua L O 于1983 年提出了著名的經典蔡氏電路(Chua’s circuit),其動力學行為豐富,取得了廣泛的應用,成為混沌科學研究的熱點對象[1-2]。蔡氏電路最核心之處是蔡氏二極管,其結構復雜,因此物理實現存在著較多的困難。諸多學者對蔡氏二極管的硬件電路設計給予了研究:文獻[3]采用標度化技術[4]設計了兩類無感蔡氏電路;文獻[5]對蔡氏二極管的設計提出了用分段線性正電阻的設計方法;文獻[6-8]采用憶阻器替代蔡氏二極管的方法設計了蔡氏電路;文獻[9]設計了分數階蔡氏電路。上述采用標度化技術的方法符合工程規范,但不遵循蔡氏電路方程;分段線性電阻設計方法,改進后的電路還保留電感,這對集成電路大規模實現還存在挑戰;憶阻器、分數階蔡氏電路,還只是在理論層面上的設計,目前還沒有實際可行的硬件電路。盡管蔡氏電路經過近40 年的研究,設計出的各種電路仍然不夠完善,還存在各種問題。
針對上述的改進方法和出現的問題,在遵循電路方程和參數的基礎上,設計易于用普通電子元件實現大規模集成的蔡氏電路方案。本文在研究蔡氏電路方程后,對非線性單元函數的元素重新歸類,根據新的非線性函數特性曲線,提出3 類三次型非線性函數,設計了功能全同和拓撲等效的兩類蔡氏電路,方程簡練,硬件調試方便,適用于混沌保密通信,為大規模集成實現提供了理論及技術基礎。
1 蔡氏電路方程
蔡氏電路是混沌領域工作者取得的第一個物理成果,它開創了混沌電路的新紀元,得到了廣泛的研究,歸一化方程為
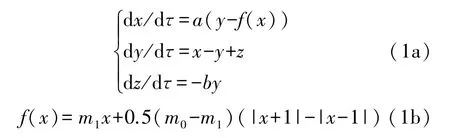
f(x)為系統函數的非線性單元,即蔡氏二極管,其中m0=-1/7、m1=2/7,a、b為參數,典型值分別為:10、15。
2 三次型非線性函數設計
2.1 飽和特性函數的設計
蔡氏電路的實現,關鍵是非線性單元的電路設計,將式(1b)的m1x部分歸為線性項,式(1a)改為dx/dτ=a(y-m1x-f′(x)),改進的式(1b)為

不考慮m0、m1情況下,式(2)表示的蔡氏二極管的核心部分寫為: 0.5(|x+1 |-|x-1 |),是一種具有飽和特性的函數,也可寫為式(3),f′(x)=(m1-m0)h(x),式(3)的波形是分段線性的三折曲線,如圖1 所示。
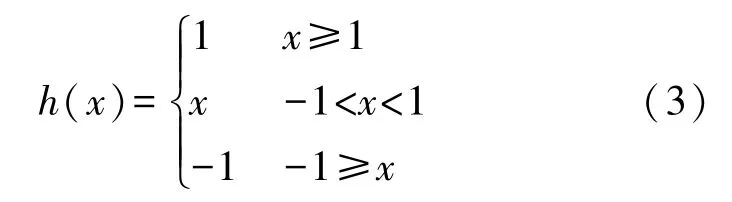

圖1 飽和函數特性曲線
2.2 三次型函數的設計與分析
圖1 所示的h(x)曲線,與最高次為x3的多項式函數曲線局部相似,中斜外平,這類函數統稱為三次型,文獻[10]利用集成運放的限幅特性來實現,本文提出的與圖1 近似的三次型曲線有:三次方函數曲線、Logistic 函數曲線、反向并聯二極管伏安曲線,如圖2 所示,與之對應的函數為式(4)、(5)、(7)。
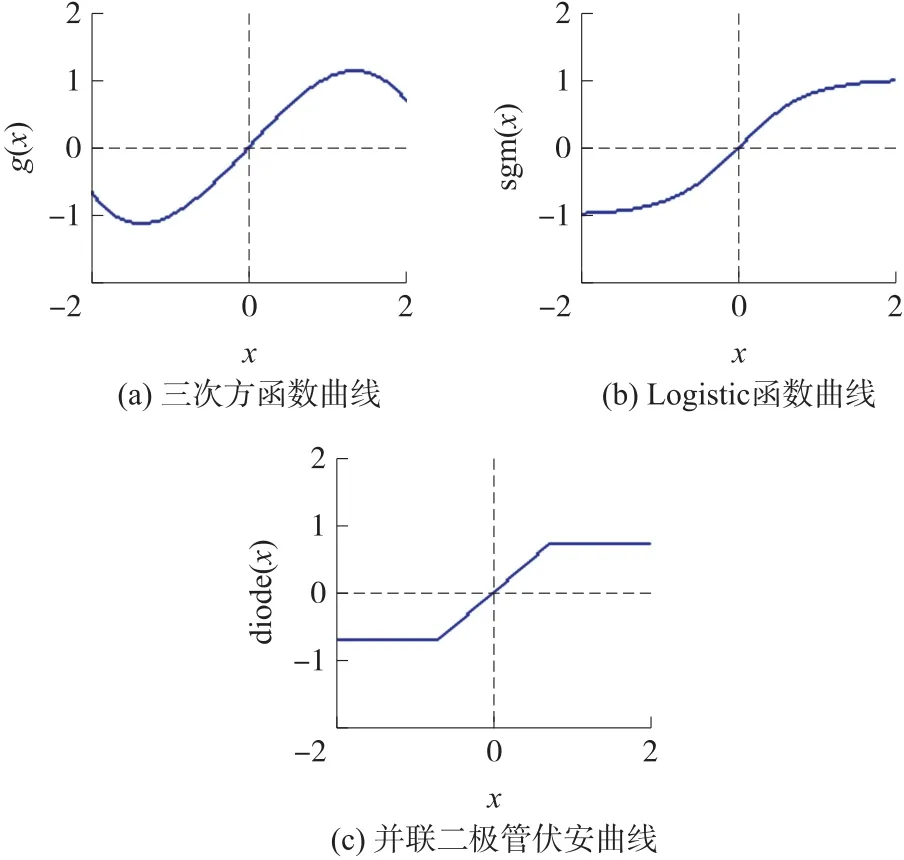
圖2 三次型函數特性曲線
三次方函數
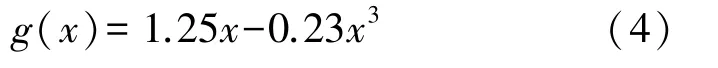
Logistic 函數
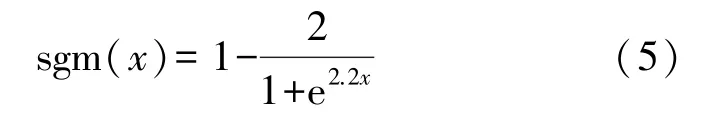
sgm(x)由sigmoid(x)函數變換而來,起源于生物學
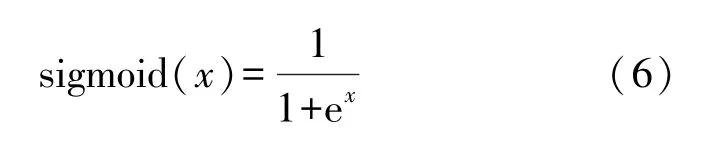
反向并聯二極管伏安特性函數
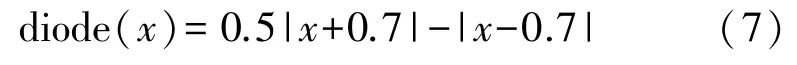
diode(x)函數來源于反向并聯二極管伏安特性函數
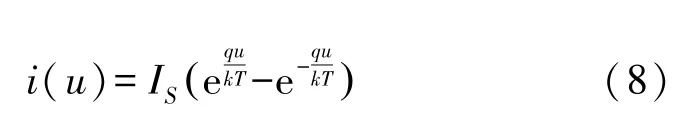
式中,u是二極管端電壓,i(u)是流過二極管的電流,IS為二極管反向飽和電流,在常溫下,kT/q=26 mV,工程實際中,二極管導通后電壓基本不變,式(7)是反向并聯二極管的伏安特性的近似公式,適用于在二極管導通電壓“0.7 V”附近的伏安特性函數,式(8)的電流以指數顯著變化,不宜直接作為蔡氏二極管的函數使用。將二極管伏安特性的導通“電壓”歸一化為以數字表達的“0.7”,反向并聯二極管兩端電流-電壓關系即為式(7),與式(1b)相比只是“0.7”和“1”差別,Chua L O 在文獻[1-2]設計的蔡氏電路,轉折點實際電壓也不是“1”伏,受限于當時的技術,改變物理電路太難,默認為“1”伏,理論上,二極管實現的蔡氏電路與經典蔡氏電路是功能全同的。
式(4)、(5)與式(3)的特性曲線只是在波形上是相似的,函數只有數學意義,而式(7)具有工程背景和明確的物理意義;式(4)函數的物理硬件實現需要兩個乘法器,式(5)函數在物理上用基本電子元件來實現目前還比較困難,式(7)函數只需兩個二極管反向并聯即可實現,十分簡潔,在物理特性上與經典蔡氏二極管一樣同屬電壓控制電流源(VCCS)器件;式(4)、(5)、(7)取代蔡氏二極管函數式(3),是非線性單元的另外一種表達形式,所得方程與蔡氏電路是拓撲等效的。
2.3 三次型混沌系統動力學分析
在硬件電路實現之前,用虛擬仿真,獲得定性認識,在混沌電路設計上是非常有必要的,式(4)、(5)、(7)替代非線性單元式(3),得到3 類三次型函數蔡氏電路混沌系統,用MATLAB 仿真3 類系統,得到的x-y相圖分別如圖3 所示。
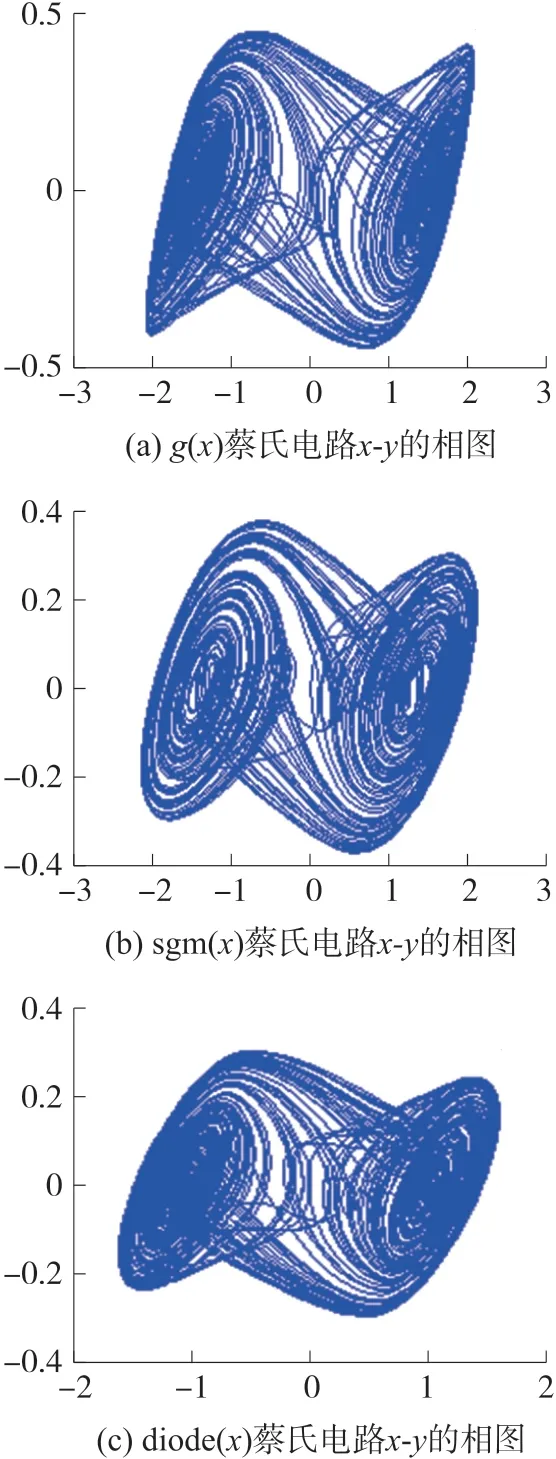
圖3 3 類三次型蔡氏電路仿真的x-y 相圖
混沌系統的Lyapunov 指數越大,系統運動越無序,動力學行為越復雜,對初值越敏感,有利于保密通信,針對設計的3 類三次型非線性函數,因為sgm(x)函數以指數變化,提高了系統的Lyapunov 指數,也符合理論實際,另外2 類減小了Lyapunov 指數,總體上差別不大,見表1。

表1 三次型蔡氏電路Lyapunov 指數
3 三次型蔡氏電路設計
所設計的三次型蔡氏電路均遵循原方程的主體結構和參數,考慮到電子元件標稱值和實際值是有誤差的,設計的電路原理圖參數是允許有誤差的,范圍相對較大,例如,圖4 中電阻R11的理論阻值為667 Ω,實際選取阻值為650 Ω~680 Ω 均可,電路焊接時,挑選精度較高,接近原理圖參數的元件,即可實現混沌電路。
三次方蔡氏電路:蔡氏電路中的核心具非線性部分電路,由式(4)三次方函數的電路代替,設計的圖4混沌電路與原蔡氏電路是拓撲等效的,也是微分同胚的,乘法器增益為0.1 V/V。
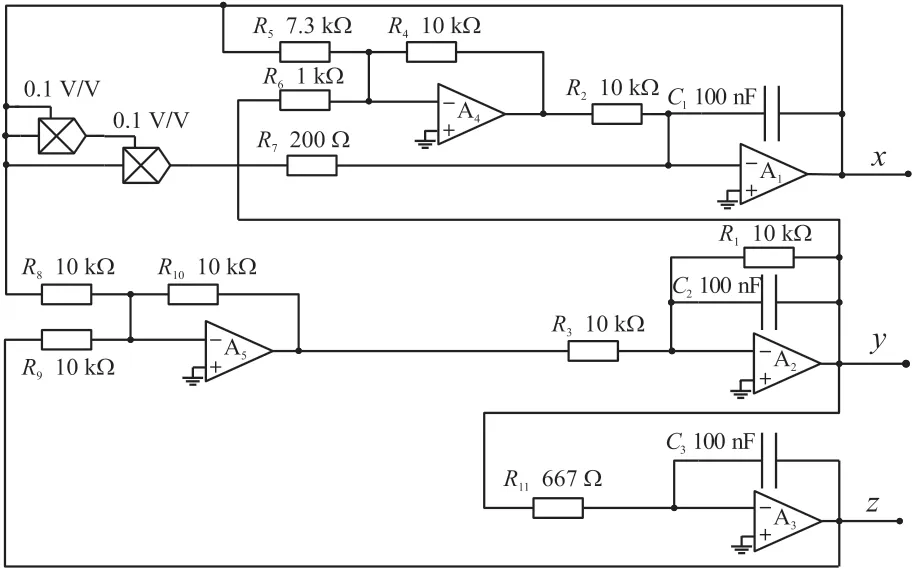
圖4 三次方蔡氏電路原理圖
二極管蔡氏電路1:電路原理圖如圖5 所示,利用二極管的鉗位作用,反向并聯二極管聯接在串聯電阻R7與電阻R5之間,實現式(7)函數的電路,直觀,元件少,理論計算也容易,電路精度高,該反向并聯二極管實現的輸入輸出是電壓-電壓的轉換關系,與式(7)表達式相同,物理量有所區別。

圖5 二極管蔡氏電路原理圖1
二極管蔡氏電路2:圖6 中,反向并聯二極管和電阻R9串聯,理想二極管的導通電阻是為0 Ω、截止為∞Ω,電阻R9=R10,R9、R10串聯有分壓功能,輸出的信號接入集成運放A5 的同向端,該反向并聯二極管的輸入輸出也是電壓-電壓的關系,如式(9a)或(9b)所示,是式(1b)核心部分的另外一種寫法,具有死區特性,波形圖如圖7 所示。
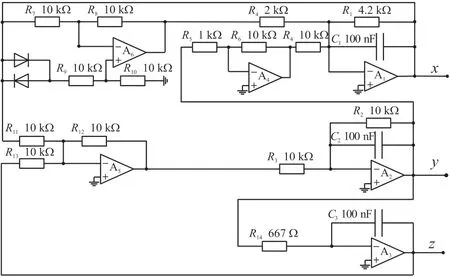
圖6 二極管蔡氏電路原理圖2
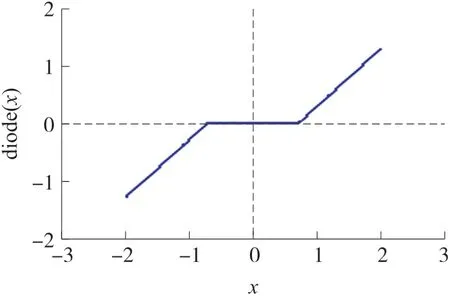
圖7 并聯二極管死區特性曲線
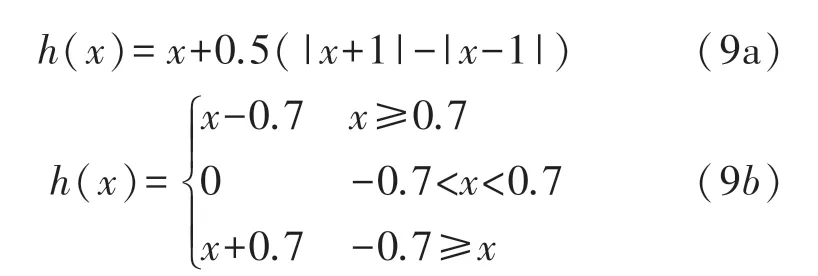
設計的如圖5、6 所示的二極管蔡氏電路,與理論是有誤差的,二極管反向不是完全截止的,二極管導通后電壓也并非完全“0.7 V”不變,從工程方面來看實際影響很小,功能與蔡氏電路是全同的。
3 類三次型蔡氏電路物理實驗相圖如圖8所示。

圖8 三次型蔡氏電路物理電路x-y 相圖
4 混沌保密通信電路設計
以本文提出的三次方蔡氏電路為例,采用反饋型驅動-響應式同步混沌保密通信制式[11]進行試驗,電路原理圖如圖9 所示,由發送端、接收端和信道三部分組成,發送端輸出信號為x1、y1、z1,接收端輸出信號為x2、y2、z2,以x1信號為載波,調制信號為m,信道傳輸的是攜帶調制信息的混沌信號x′1,解調信號為保密精度高。
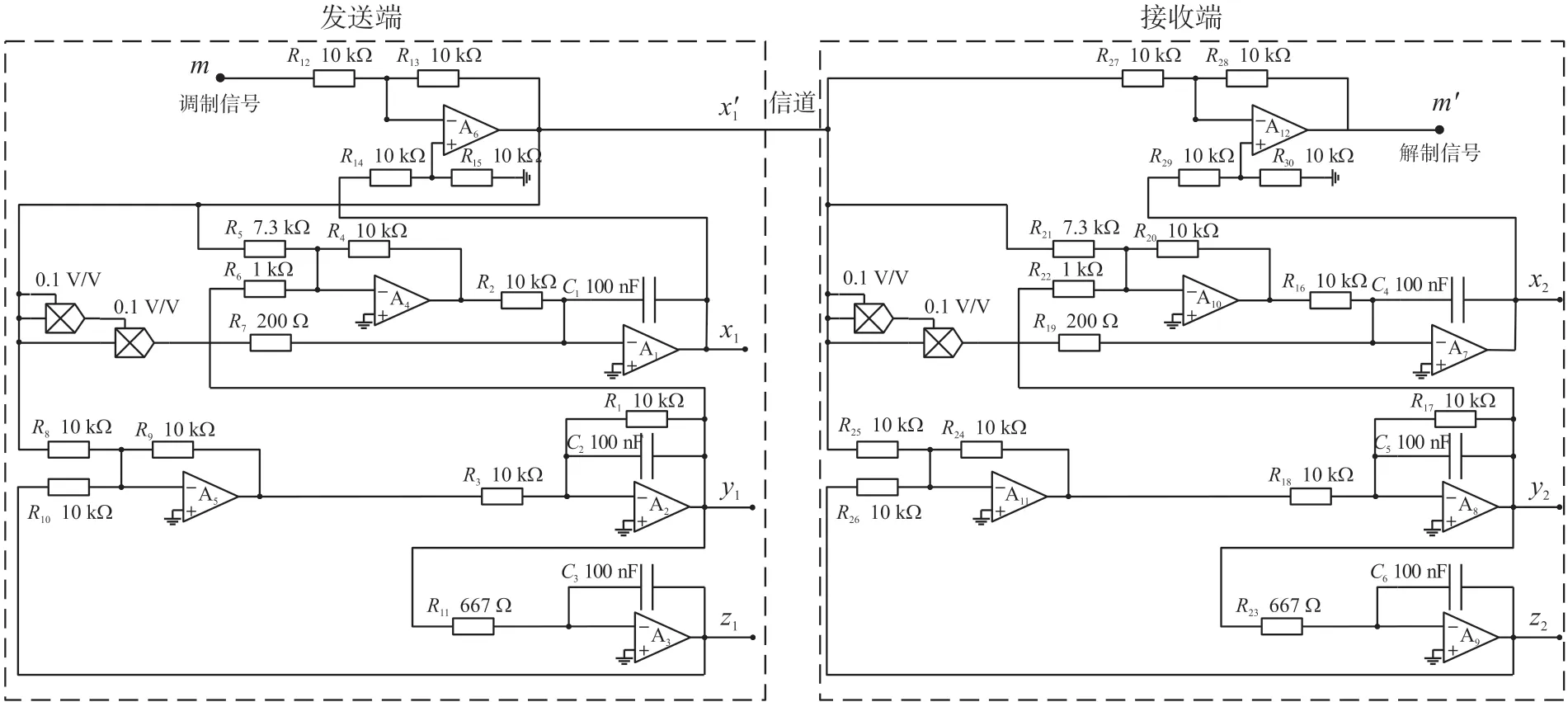
圖9 三次方蔡氏電路混沌調制保密通信原理圖
只要保密通信系統的收、發電路對應元件的參數相同,就可以達到設計的實驗效果。圖10(a)、(b)、(c)是物理電路實驗時,示波器顯示的收、發端同步時x1-x2,y1-y2,z1-z2的相圖,同步得很好。

圖10 混沌調制保密通信收、發端同步相圖
圖11(a)是將10 mV 的正弦調制信號m加入保密電路時,輸出的x1-y1相圖,依然是雙渦卷混沌;圖11(b)是系統攜帶加密信號m時的發送端x1波形圖,接收端x2波形圖,觀察不到二者的差別;圖11(c)是調制信號波形圖與解調信號波形圖,完全一致。此外,蔡氏電路的狀態變量以電壓形式輸出,單位是伏特,調制信號是毫伏級,因此該保密通信電路噪聲系數小于10-3,保密系統可靠。

圖11 調制解調過程波形圖
5 結語
1983 年Chua L O 提出的經典蔡氏電路,是混沌電路工程的典范,具有里程碑意義,非線性單元為核心部分,屬于三次型函數,是分段線性的三折曲線,為后續分段線性混沌系統帶來許多啟示[12]。
(1)本文針對非線性單元的核心部分,在遵循蔡氏電路結構和參數的前提下,提出3 類三次型函數,設計了3 類蔡氏電路,均易于搭建實際混沌電路。
(2)本文提出的三次型蔡氏電路,是全同或者拓撲等效的蔡氏電路,方程簡練,分析方便。
(3)本文提出的三次型蔡氏電路,適合于混沌保密通信,尤以主從式反饋型驅動-響應式混沌調制保密通信為優。

