賞析數(shù)學(xué)核心素養(yǎng)視角下一道高考導(dǎo)數(shù)真題

蘇吉超

(安徽省亳州市第二完全中學(xué))

導(dǎo)數(shù)試題多為高考試題中的壓軸試題,主要涉及利用導(dǎo)數(shù)研究函數(shù)的單調(diào)性、極值和最值,探究曲線的切線,證明不等式等.此類試題注重考查學(xué)生的分類討論思想、運算求解能力和推理論證能力.

母題 (2021年全國乙卷文21)已知函數(shù)

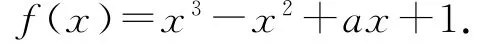
(1)討論f(x)的單調(diào)性;

(2)求曲線y＝f(x)過坐標(biāo)原點的切線與曲線y＝f(x)的公共點的坐標(biāo).

分析 (1)對函數(shù)f(x)求導(dǎo),討論導(dǎo)函數(shù)與零的關(guān)系,進(jìn)而得出f(x)的單調(diào)性情況.

(2)先設(shè)出切點,表示出切線方程,根據(jù)切線過原點,可求得切線方程,將切線方程與曲線y＝f(x)聯(lián)立,即可求得公共點的坐標(biāo).

解 (1)對f(x)求導(dǎo)得f′(x)＝3x2-2x＋a,則導(dǎo)函數(shù)的判別式為Δ＝4-12a.

令f′(x)＞0,解得x＜x1或x＞x2,令f′(x)＜0,解得x1＜x＜x2,所以f(x)在(-∞,x1),(x2,＋∞)上單調(diào)遞增,在(x1,x2)上單調(diào)遞減.

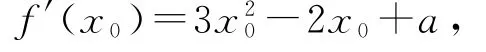
所以切線方程為

令x3-x2＋ax＋1＝(a＋1)x,即x3-x2-x＋1＝0,解得x＝1或-1,所以曲線y＝f(x)過坐標(biāo)原點的切線與曲線y＝f(x)的公共點的坐標(biāo)為(1,a＋1)和(-1,-a-1).

【數(shù)學(xué)建模】本題所涉及的模型主要有兩個:一是利用導(dǎo)數(shù)研究函數(shù)的單調(diào)性問題,這里需要學(xué)生能夠根據(jù)所給函數(shù)的導(dǎo)數(shù),合理地將所求問題轉(zhuǎn)化為求解二次函數(shù)問題,解題的難點在于分類討論思想的應(yīng)用.二是導(dǎo)數(shù)的幾何意義模型,這里需要關(guān)注所求切線是“過某點”還是“在某點”,以防掉入試題陷阱.

【數(shù)學(xué)運算】導(dǎo)數(shù)試題的顯著特點就在于運算量較大,學(xué)生不僅要能夠正確求出所給函數(shù)的導(dǎo)函數(shù),還要能夠根據(jù)切線方程的求解方法列出方程,并且能夠正確化簡.

【邏輯推理】在此問題的求解過程中要能夠正確進(jìn)行分類討論,根據(jù)判別式進(jìn)行正確的分類討論,再依據(jù)分類的標(biāo)準(zhǔn)求解所給函數(shù)的單調(diào)區(qū)間.

【數(shù)學(xué)抽象】這里涉及了一個過指定點的切線問題,相比于以往的這類問題,考查角度不同,此題一反常態(tài),不是直接考查切線方程的求法,而是求過指定點的切線與曲線的交點坐標(biāo).

【空間想象】在解決函數(shù)的單調(diào)區(qū)間問題時,學(xué)生要具備一定的想象能力和作圖能力,能夠正確作出二次函數(shù)的圖像是第(1)問求解的保障.同時,對于第(2)問的求解,如果能夠正確作出草圖,也會使得問題更加直觀.

為了更好地對三次函數(shù)背景下的導(dǎo)數(shù)試題進(jìn)行求解,下面給出兩道數(shù)學(xué)試題.

練習(xí)1 已知三次函數(shù)f(x)＝x3＋ax2-6x＋b,a,b∈R,若函數(shù)f(x)的圖像在x＝1處的切線方程為12x＋2y-1＝0.

(1)求函數(shù)f(x)的解析式;

(2)求函數(shù)f(x)的極小值;

(3)若存在x∈(0,＋∞),使得3lnx≥f′(x)＋|2m-1|成立,求實數(shù)m的取值范圍.

分析 (1)求出函數(shù)的導(dǎo)數(shù),利用導(dǎo)數(shù)的幾何意義求出a,求出切點坐標(biāo),代入函數(shù)的解析式,求出b,然后可得函數(shù)的解析式.

(2)利用導(dǎo)數(shù)求出f(x)的單調(diào)性即可.

(3)令g(x)＝3lnx-f′(x),再利用導(dǎo)數(shù)求出g(x)的最大值,然后轉(zhuǎn)化不等式求出m的范圍.

解 (1)因為f′(x)＝3x2＋2ax-6,直線12x＋2y-1＝0的斜率為-6,所以f′(1)＝-6,所以

(2)f′(x)＝3x2-3x-6,由f′(x)＝3x2-3x-6＝0,可得x＝2或-1.

由f′(x)＜0,可得-1＜x＜2,由f′(x)＞0,可得x＜-1或x＞2,所以f(x)在(-1,2)上單調(diào)遞減,f(x)在(-∞,-1)和(2,＋∞)上單調(diào)遞增,所以f(x)的極小值為f(2)＝-9.

(3)令g(x)＝3lnx-f′(x)(x＞0),則

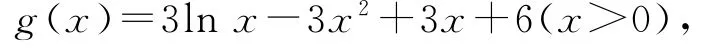
所以

練習(xí)2 (2022年北京卷20)已知函數(shù)

f(x)＝exln(1＋x).

(1)求曲線y＝f(x)在點(0,f(0))處的切線方程;

(2)設(shè)g(x)＝f′(x),討論函數(shù)g(x)在[0,＋∞)上的單調(diào)性;

(3)證明:對任意的s,t∈(0,＋∞),有

分析 (1)考查求切線方程,只需求出導(dǎo)函數(shù),再求出過點(0,f(0))的切線斜率,按照求直線方程的點斜式求解即可.

(2)引入輔助函數(shù),通過輔助函數(shù)的單調(diào)性求原函數(shù)的單調(diào)性.

(3)構(gòu)造函數(shù),通過求函數(shù)的單調(diào)性證明不等式.

解 (1)因為f(0)＝0,所以切點坐標(biāo)為(0,0).

所以h(x)在[0,＋∞)上單調(diào)遞增,所以

所以g′(x)＞0在[0,＋∞)上恒成立,所以g(x)在[0,＋∞)上單調(diào)遞增.

(3)原不等式等價于

令m(x)＝f(x＋t)-f(x)(x≥0,t＞0),即證m(x)＞m(0),因為

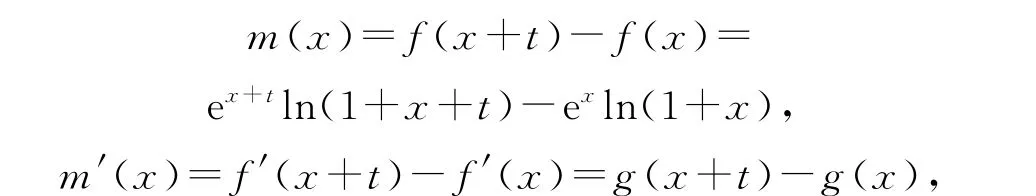
由(2)可知g(x)在[0,＋∞)上單調(diào)遞增,則

則m′(x)＞0,所以m(x)在(0,＋∞)上單調(diào)遞增,又因為x≥0,t＞0,所以m(x)＞m(0),故命題得證.