強基計劃數學備考系列講座(8)
——平面向量

王慧興正高級教師 特級教師

(清華大學附屬中學)

1 知識與技能

1.1 知識梳理

這部分內容要求學生整體把握向量分析路徑,培育發展數學核心素養,核心知識如表1所示.

表1

1.2 要點解析

1)向量共線

圖1

(2)平行四邊形法則:如圖2所示,以O為起點,

圖2

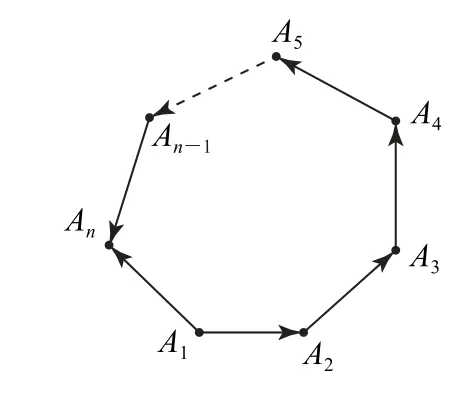
圖3

圖4

3)共線向量基本定理

向量a和非零向量b共線的充要條件是存在唯一實數λ,使得b＝λa(λ∈R{0}).

4)共面向量基本定理

圖5

5)向量的數量積

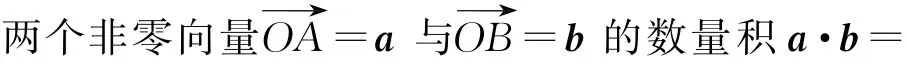
6)幾何向量

圖6

(2)定差冪線定理——垂直的平方差充要條件或平方和條件:AC⊥BD?AB2-AD2＝CB2-CD2?AB2＋CD2＝AD2＋BC2.

(3)△ABC的三邊中線相交于G、三邊中垂線相交于O、三邊上的高線相交于H、三個內角的平分線相交于I,依次稱為△ABC的重心、外心、垂心、內心;一個角的內角平分線與另外兩個角的外角平分線相交,得到三個點Ia,Ib,Ic,稱為△ABC的旁心.用向量表征△ABC的五心,得到如下充要條件:

2 典例精析

向量分析即計算與推理,其基本路徑是基于基本定理的坐標代數化和基于基本定理的幾何計算推理路徑,前者是面向高考的常態教學熱點,本文主要探究幾何情境中向量計算與推理基本路徑.

2.1 提升向量運算境界

向量既有直觀的幾何表示,又有代數運算的靈活性,這意味著它既有自身的靈活性,也有廣泛的交互應用功能.因此,向量運算的題型會呈現出千姿百態,要從以下幾個方面進行向量計算與推理:1)向量的基本運算;2)基于幾何結構助推向量運算;3)以基向量表征向量運算;4)基于共面基本定理的坐標代數化;5)基于共面基本定理的幾何計算路徑.方法1 如圖10 所示,考慮特殊情形,作

圖7

圖8

圖9

圖10

Rt△ABC,使得∠B＝90°,AB＝3,AC＝5,則

圖11

方法3 由奔馳定理,點O在△ABC內部,記△OBC,△OCA,△OAB的面積分別為SA,SB,SC,且SA∶SB∶SC＝1∶2∶3,所以

圖12

2.2 幾何環境中向量分析路徑

選擇具有已知信息的向量作為基向量,根據平面向量基本定理與共線向量基本定理合理表征,建立指向目標的向量聯結,或指明幾何計算方向,再作幾何分析,完成幾何計算.

圖13

圖14

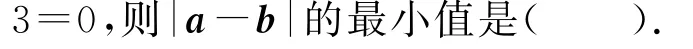
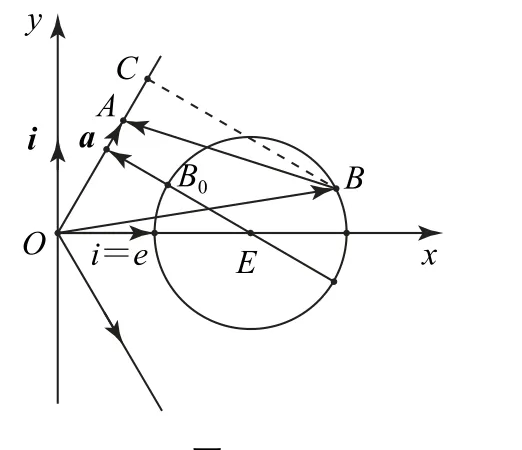
圖15

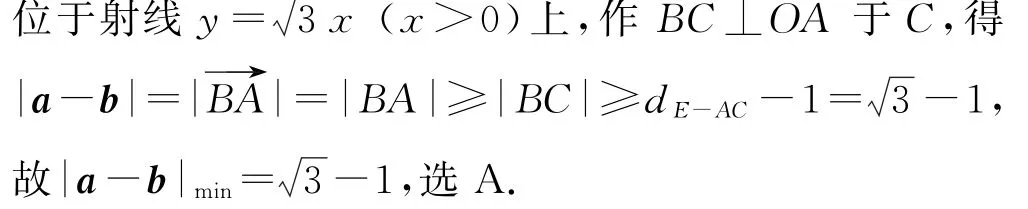
2.3 識別奔馳定理結構,分離指向目標的比例數據

2.4 以幾何結構,構造向量目標

以特定的幾何結構指向目標建立向量關系,訓練極端性思維,發展組合技能.

例7 給出4個平面向量,使得其中任意兩個的和向量總與另外兩個的和向量垂直.

如圖16 所示,取正△ABC,記其中心為O,R為其外接圓半徑,r為其內切圓半徑,在其內切圓上任取一點P,則

圖16

2.5 向量指向代數計算與幾何推理

1)向量與代數

顯然,應用柯西不等式可得fmax＝1,但得不出最小值.考慮f的分子和分母的代數結構,可以發現呈現出數量積與向量模長特征,因此,根據a,b,c,d∈[2,4],構造如圖17所示的正方形區域,建立動態向量夾角重新表征f.

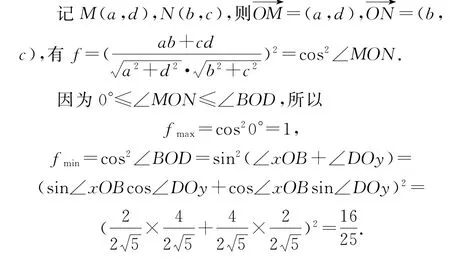
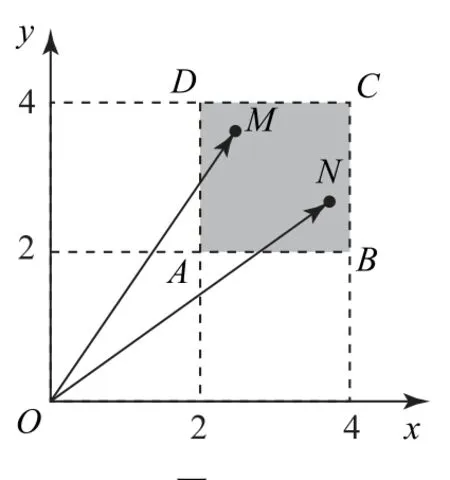
圖17

2)向量與解析幾何

例9 求坐標原點O關于直線l:2x-y-2＝0的對稱點A.

圖18

圖19

3 實戰演練

圖20

圖21

A.I1＜I2＜I3B.I1＜I3＜I2

C.I3＜I1＜I2D.I2＜I1＜I3