解答平面向量最值問題的常用策略
2022-10-23 07:18:56陳立云
高中數理化 2022年17期
陳立云
(福建省莆田市莆田第十一中學)
作為連接高中數學代數與幾何圖形的樞紐,平面向量發揮著重要的作用.它是高考數學考查頻率較高的內容,其中平面向量的最值問題尤為常見,短小精悍的問題往往蘊含著“數”與“形”的深層意義,解答策略和思路靈活多變,因此需要學生熟練掌握求解平面向量最值問題的常用策略.本文結合具體例題,分析不同的解題策略的應用思路與解題步驟.
1 借助坐標運算求解
借助坐標運算求解平面向量最值問題的關鍵在于建立平面直角坐標系,利用坐標運算建立函數解析式,再根據函數定義域求對應的最值.運用坐標運算策略解題時,要先建立合適的平面直角坐標系,對未知動點進行假設,再結合問題所給條件,將所求的向量運用坐標表示,并進行運算得到相關函數解析式,最后在函數定義域內,求出函數對應的最值.


圖1

解 建立如圖2 所示的平面直角坐標系,則B(2,0),C(2,1),D(0,1).設Q(x,1),P(2,y)(0≤x≤2,0≤y≤1).

圖2


圖3

解 如圖4所示,以點A為原點,邊AB所在直線為x軸,邊AD所在直線為y軸建立平面直角坐標系,設點
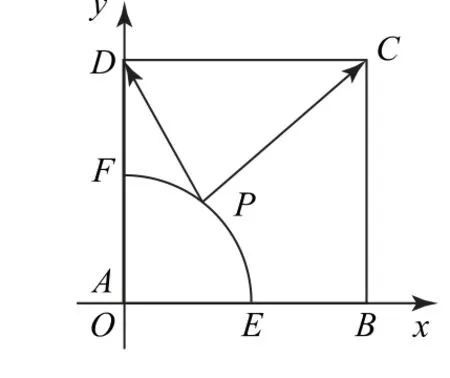
圖4

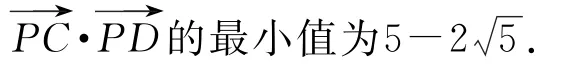
2 構造幾何圖形求解
構造幾何圖形策略解答平面向量最值問題,主要是根據問題中的已知條件構造三角形、圓等幾何圖形,賦予問題具體的幾何意義,運用幾何性質和定義解答.構造幾何圖形求解這一類問題,常見的解題步驟為分析題意,根據所給條件構造對應的幾何圖形,使問題具有具體的幾何意義,再探索最值對應的幾何圖形情況,運用幾何性質或定理求出最值.


圖5

圖6



圖7
平面向量最值問題靈活多變,根據內容形式的不同可以采取不同的解題策略.坐標運算、構造幾何圖形等都是解答平面向量最值問題較為常見的解題策略,也都是學生需要熟練掌握的策略.合理運用這些策略,能使較為復雜抽象的問題簡單化、直觀化,從而提高解題效率.
猜你喜歡
小學生學習指導(低年級)(2022年9期)2022-10-08 03:12:02
中學生數理化·中考版(2022年8期)2022-06-14 06:55:52
小學生學習指導(低年級)(2021年4期)2021-07-21 01:59:26
教學考試(高考化學)(2021年2期)2021-05-30 06:15:52
中學生數理化·高一版(2020年3期)2020-04-21 08:03:20
中學生數理化(高中版.高考理化)(2020年2期)2020-04-21 05:32:50
小學生作文(低年級適用)(2019年9期)2019-10-08 08:37:10
中學數學雜志(2019年1期)2019-04-03 00:35:46
中學生數理化·中考版(2018年11期)2019-01-31 06:18:02
數學大世界(2018年1期)2018-04-12 05:39:14

