向量“圓”析構建新課堂 核心素養探究新教材
——基于數學核心素養的平面向量微專題課例

徐成周

(濟南大學城實驗高級中學)

基于培養學生解決平面向量問題能力的主要目標,根據我校高一學生的實際學情,以微專題的教學模式設計教學方案,充分發揮教師的引導作用和調動學生的主觀能動性,提高學生的數學思維參與度,深化學生求解平面向量問題的能力,助力提高學生的數學核心素養.

1 問題提出的背景

高中數學教學側重于按照教材中的章節內容開展數學知識的講解,或者以“對點訓練”的方式,進行解題思維的培養.這些方式雖然可以較為全面地使學生掌握數學知識,但是從宏觀的角度看,不利于學生脈絡清晰地構建完整的數學知識體系.如果可以在高中數學教學中,融入微專題的教學模式,那么既有利于督促學生構建完整的數學知識體系,疏通知識脈絡,又可以高效提高學生的解題能力.

1.1 微專題的含義

微專題課程,即將教學過程中的某一類問題,經過篩選、整理、提煉,凝練為一個教學課題,開展學科課程教研.微專題經常選用一些價值高、有意義、科學有效的小型專題作為教學的切入點,可以對學生進行專項訓練,具有“切口小、周期短、時效高”的基本特征,從而達到“課程解決問題,專項研究對策,學習結果扎實”的成效.

1.2 微專題教學模式融入高中數學教學的重要性

在“雙減”背景下,微專題教學可以簡明扼要地在教師指導下開展教學活動,防止學生在數學學習中一味地采用“題海戰術”,可極大地降低學生的學習負擔,使數學學習變得高效.

例如,教師在開展“平面向量”這部分知識教學時,發現大多數學生不能做到“學以致用、舉一反三、一題多解、靈活通融”,經常以一種思維模式思考題目,從而走入死胡同.此時設計以平面向量解題為主題的微專題,可以促使他們在解題中更加準確地進行判斷與決策,及時采用最優的思維方式進行思考.與此同時,微專題教學模式下的數學課堂靈活性強,并將前、后知識模塊進行多方面聯系,極大地促進學生對數學知識內在本質的探索與理解,從而全方位提高學生的數學核心素養.

1.3 微專題教學模式的基本原則

1)精準打擊,逐個擊破

微專題可以分解為“微”和“專題”,是通過小課題、小專題的方式對教學知識進行深化處理.例如,對于“立體幾何、統計與概率”這樣的大專題知識進行更加細致地解剖和分析,做到精準打擊、點點擊破,幫助學生進行查缺補漏.

2)以生為本,深化思維

微專題教學模式的構建是建立在教師對高中學生認知結構的了解基礎上,強化學生在教學活動中的主體地位.因此,教師要深入了解高中學生在數學上的認知結構,教學要遵循學生的學習規律.教師要采用有效的方式幫助學生調動自身的學習思維,從而從本質上切實提高他們學習的效率.

3)見微知著,融會貫通

教學是教師的“教”和學生的“學”的交互過程,只有教和學有機結合、相互促進,才能真正地達到教學目的.開展微專題教學,可以使學生注意到平時練習中忽視的問題,對潛藏的薄弱之處進行查缺補漏;可以使教師對教材和學生進行更加深入的了解.通過微專題學習,學生可以對知識點進行整理歸納以及重構,將知識點和題目進行連接,對題目進行對比,真正做到融會貫通.

2 微專題教學課程設計——以平面向量問題教學為例

2.1 教材內容分析

向量作為溝通“代數”“幾何”“三角”的橋梁,對中學數學知識框架的構建起著更新和完善的作用,是從豐富的生活實際和物理素材中抽象出來的.向量具有豐富的代數運算法則,與之前所學的代數運算具有相似之處,也有不同之處;向量是一種工具,兼具“代數”和“幾何”的屬性.解決向量相關題目要讓學生去體會在不同角度下的思維模式,進而提高提出問題、分析問題、解決問題的能力.

2.2 教學目標設置

提高學生充分挖掘題目幾何特性的能力,從代數視角研究向量的同時,可以在幾何的思維方式下,具體形象地思考問題,從而找到題目的最優解.

充分挖掘題目中條件和結論的關系,體會其中的形成過程,培養學生觀察、聯系、類比、抽象、概括、歸納、實踐等方面的能力.

2.3 學生學情分析

在解決平面向量問題時,學生習慣性采用代數的方法,有時經過大量的計算而不得其解.若從圖形視角來思考具有豐富幾何內涵的向量問題,有時會迎刃而解.

2.4 教學策略分析

采用“問題串”的教學方法,通過“拋出問題,引導學生思路,教師點撥引導”三者結合,促進學生的理解和掌握.

在設置“問題串”時,注意題目側重點類型的多樣性,題目和題目之間具有難度梯度,層層深入,做到模塊與模塊之間的有機聯系和整合.

2.5 教學方法與教學手段

1)問題引導教學法

2)“問題串”式啟發教學

3)小組合作探究學習

2.6 教學過程

1)溫故知新

教師:什么是向量?

學生:向量是既有大小又有方向的量.

教師:向量的大小是向量的代數特征,向量的方向是向量的幾何特征,向量具有“代數”和“幾何”的二重性,今天我們重點從“幾何”的角度來研究向量問題.

設計意圖 通過向量的定義引出向量的二重性,溫故而知新,深入挖掘向量的特征.

2)因勢利導——從幾何的角度研究向量問題

教師:向量a,b如圖1所示,利用向量加法的三角形法則作出a＋b;向量a,b如圖2所示,利用向量加法的平行四邊形法則作出a＋b.

學生:

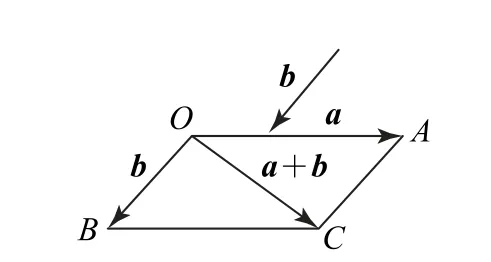
圖4

設計意圖 從基本知識點切入,引導學生從幾何的角度來思考向量的運算問題.

3)牛刀小試

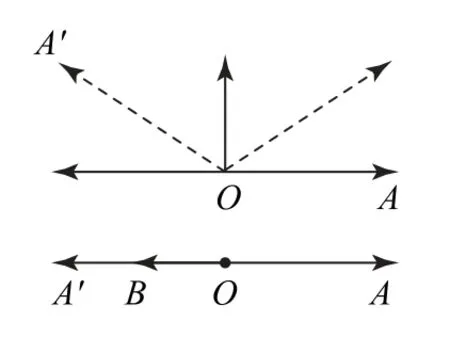
圖5

設計意圖 從基礎題入手,引導學生從幾何的角度剖析題目條件,作出相應圖形,從而分析出答案.

問題2 設向量a,b,c滿足a＋b＋c＝0,且滿足(a-c)⊥b,a⊥c,請加入一個條件,設計問題.

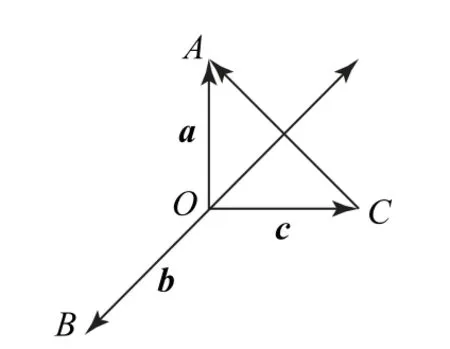
圖6

4)進階提升

通過圖7可知,過圓心時有最大值.

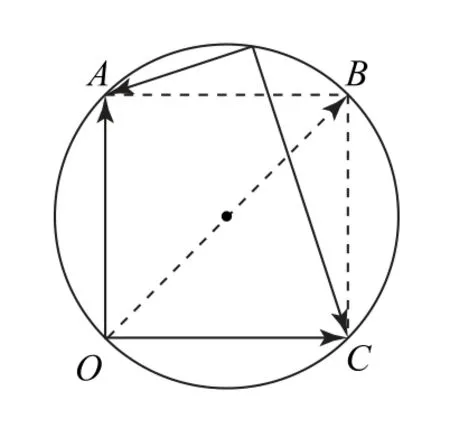
圖7

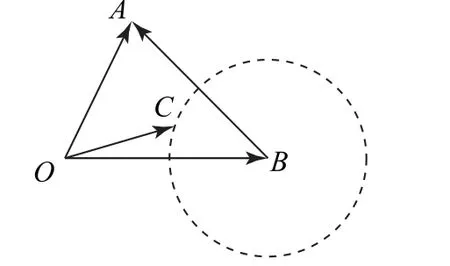
圖8

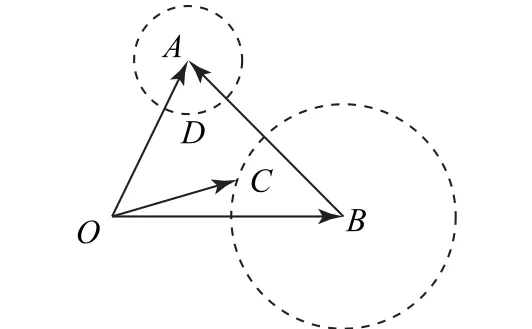
圖9

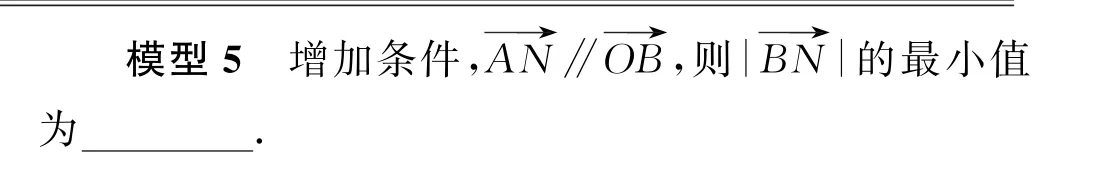
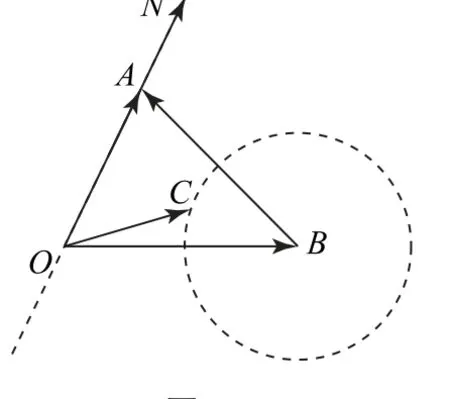
圖10

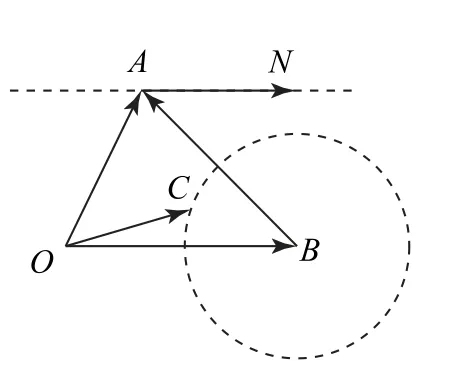
圖11

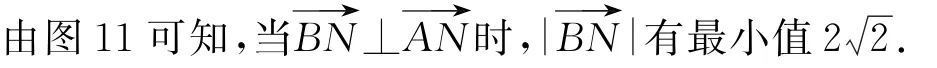
設計意圖 以一個基礎模型切入,通過不斷變化題目條件,培養學生舉一反三的能力;不斷豐富題目條件,層層深入,拓寬學生解決向量問題時的思路,學會用幾何的視角思考向量問題.

3 課堂總結

為了更加突出微專題課程的課堂教學思路,可以通過框架圖的形式厘清課堂脈絡,以本節課為例,可板書以下框架圖(如圖13).

圖13

4 小結

本文研究的問題是在微專題教學模式下,培養學生在解決平面向量問題時的幾何思路.

通過教學實踐,在微專題教學模式下進行教學需要注意:選擇的問題應該具有典型性,通過變換和豐富題目條件,培養學生舉一反三的能力;幾何方法在解決平面向量問題時,可以進行推廣和一般化,幫助學生在解決問題時做到深入淺出;在組織和培養學生的解題能力時可以按照問題串的方式進行展開,歸納和總結解決數學問題的方法.

總而言之,微專題教學模式在深化學生解決問題的能力時可以起到針對性的效果,教師需要結合教學實踐,在課題的選擇和組織展開上不斷鉆研和總結,真正提高學生的數學素養.