基于動態逆的渦軸發動機自適應模型建模方法研究

夏天乾，徐植桂，吳金棟，汪勇

(1. 中國航發動力控制系統研究所，江蘇 無錫 214013；2. 南京航空航天大學 江蘇省航空動力系統重點實驗室，江蘇 南京 214016)

0 引言

如何更好地建立渦軸發動機自適應模型是實現性能尋優控制、模型預測控制及在線故障診斷等先進控制技術的基礎與前提[1]。一個良好的渦軸發動機自適應模型不僅可以準確表達發動機額定工作下的系統動態，而且需具備實時反映發動機服役期內部件退化對發動機性能影響的能力[2]。

近年來，隨著神經網絡與深度學習的快速興起，促進了基于數據驅動的渦軸發動機機載自適應建模方法的進一步發展[3]。然而，隨著服役時間的延長，渦軸發動機各部件不可避免地發生退化，造成發動機的關鍵性能參數出現明顯偏差；此外，考慮到發動機部件退化因子無法直接測量獲得[4]，因此有必要在快速、準確估計發動機退化情形的基礎上，構建高保真的渦軸發動機自適應模型。

自卡爾曼(Kalman)估計方法出現以來，以Kalman濾波估計器為核心，根據發動機實測狀態量的變化估計發動機性能退化的自適應建模方法應運而生，出現了很多相關的應用成果[5]。LUPPOLD R等[6]率先提出了基于卡爾曼濾波思想的發動機自適應建模方法，根據可測輸出實時估計發動機性能退化因子。為彌補線性卡爾曼估計方法只能用于小范圍的缺陷，SAAB S S采用拓展卡爾曼濾波的方法[7]，通過在線擬合發動機的狀態變量模型，實時求解卡爾曼增益矩陣，拓寬了卡爾曼估計技術的適用范圍。顯然這種處理給控制系統設計、計算都帶來較大的復雜度。此外，POURBABAEE B等[8]采用多模型混合卡爾曼濾波器實現對燃氣輪機傳感器的故障檢測、隔離和識別，可準確檢測發動機故障。張海波等提出了一種基于機載非線性發動機模型，且具有輸入端積分補償的卡爾曼濾波器估計器的發動機自適應模型設計方法[9]。魯峰等提出了一種基于容積跟蹤濾波器的渦軸發動機自適應部件級仿真模型構建方法，自動修正各部件的流量和效率特性圖，以進行部件氣動熱力參數計算[10]。然而，發動機的強非線性特性導致以Kalman濾波為核心的發動機自適應模型難以完全跟蹤實際發動機的輸出。基于此，肖玲斐等[11]結合滑模控制理論，設計滑模控制器，提出基于誤差反饋滑模控制的航空發動機自適應線性動態模型設計方法。但滑模控制量的切換幅度越大，抖動越明顯。在精確度要求較高的航空航天領域，這種抖動存在影響系統響應品質的可能。

綜上，本文為彌補現有技術研究的不足，提出一種基于動態逆的航空發動機自適應建模方法。

1 基于動態逆的自適應模型

動態逆作為一種多變量控制結構[12]，可對控制變量進行動態特性處理，以達到期望的特性，能對復雜的耦合非線性問題進行解耦控制[13-14]，因此在飛行控制等領域發揮著重要的作用。接下來介紹基于動態逆的健康參數估計方法。

1.1 基于動態逆的健康參數估計器

實現動態逆的前提是獲取能實時表達發動機工作特性的數學解析式。而對于渦軸發動機而言，通常可采用狀態變量模型近似表達發動機的非線性動態特性。額定狀態下，渦軸發動機狀態變量模型的表達形式為

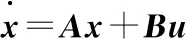
(1)

一般情況下，上式的控制輸入向量u包括旋翼總距θ0與燃油流量Wfb。而當發動機性能發生退化時，通常可用部件效率和流量特性與設計值的偏差來表征發動機的健康情況。因此，為了基于動態逆實現對渦軸發動機健康參數的實時估計，輸入向量u中還需包含部件的健康參數。由此可得基于動態逆的健康參數估計器表達式為

u=(C·B)-1·[λ-(C·A)x]
λ=K·(yreal-y)

(2)

式中：yreal代表真實渦軸發動機的可測參數；K為線性控制器的增益矩陣。若C·B非方陣時，可采用廣義逆或加號逆代替。由上式可知，當狀態變量模型的輸出可實時跟蹤真實發動機的可測輸出時，動態逆即可實現對發動機部件健康參數的最優估計。

1.2 基于神經網絡的渦軸發動機機載模型

Back Propagation(BP)神經網絡作為一種根據誤差逆向傳播算法訓練的多層前饋網絡[15-16]，可在未知系統工作屬性的前提下，學習、存儲大量的輸入-輸出映射關系，是目前應用最為廣泛神經網絡模型之一。因此本文采用BP神經網絡離線訓練獲得渦軸發動機機載模型。

為了使機載模型能更準確地反映原發動機的動態特性，采用非線性自回歸滑動平均模型結構。設渦軸發動機機載模型為2階系統，以歷史時刻的發動機控制量、健康參數、發動機的相關可測狀態參數以及當前時刻的發動機控制量、健康參數為輸入，當前時刻發動機狀態參數為輸出，如下式所示。

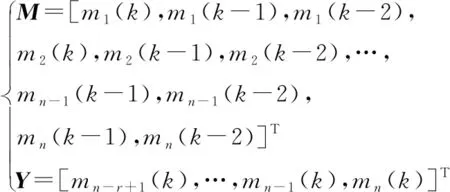
(3)

式中：M、Y分別為航空發動機機載模型的輸入、輸出向量；m為各向量中的元素；n為輸入向量的維數；r為輸出向量的維數；k為當前時刻。

2 仿真驗證

結合上述原理，可得基于動態逆的渦軸發動機自適應模型結構如圖1所示。圖1中自適應模型由渦軸發動機、基于增量式動態逆的健康參數估計器、基于神經網絡的渦軸發動機機載模型三部分組成。其中，渦軸發動機機載模型可離線獲得。由圖可知，在單個仿真步長內，發動機健康參數估計器根據渦軸發動機的可測狀態參數與渦軸發動機狀態變量模型的狀態量，實時估計發動機的健康參數，并傳遞至渦軸發動機機載模型，一起構成渦軸發動機的自適應模型。

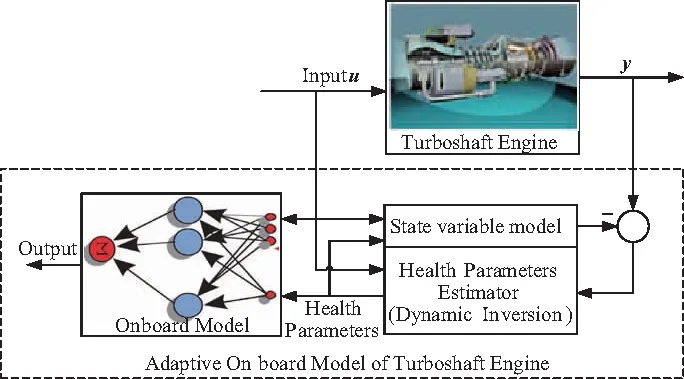
圖1 機載自適應模型結構

假設僅考慮壓氣機、燃氣渦輪的效率發生退化，則渦軸發動機機載模型表達形式如下：

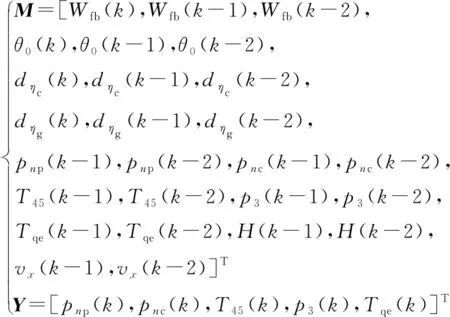
(4)

式中：k為當前時刻，是指當前周期的數據；k-1、k-2為歷史時刻，是指上周期和上上周期的數據；輸入量為歷史時刻的燃油流量Wfb、旋翼總距θ0、壓氣機效率健康參數dηc、燃氣渦輪效率退化系數dηg、動力渦輪相對轉速pnp、壓氣機相對轉速pnc、動力渦輪出口溫度T45、壓氣機出口壓力p3、發動機輸出轉矩Tqe、飛行高度H、前飛速度νx以及當前時刻的Wfb、θ0、dηc、dηg；輸出量為當前時刻的pnp、pnc、T45、p3與Tqe。因此，整個渦軸發動機機載模型包括26個輸入、5個輸出。機載模型相對測試誤差如圖2所示。由圖可知，各輸出參數相對誤差均<0.1%，精度較高，滿足要求，可用于構建渦軸發動機機載自適應模型。

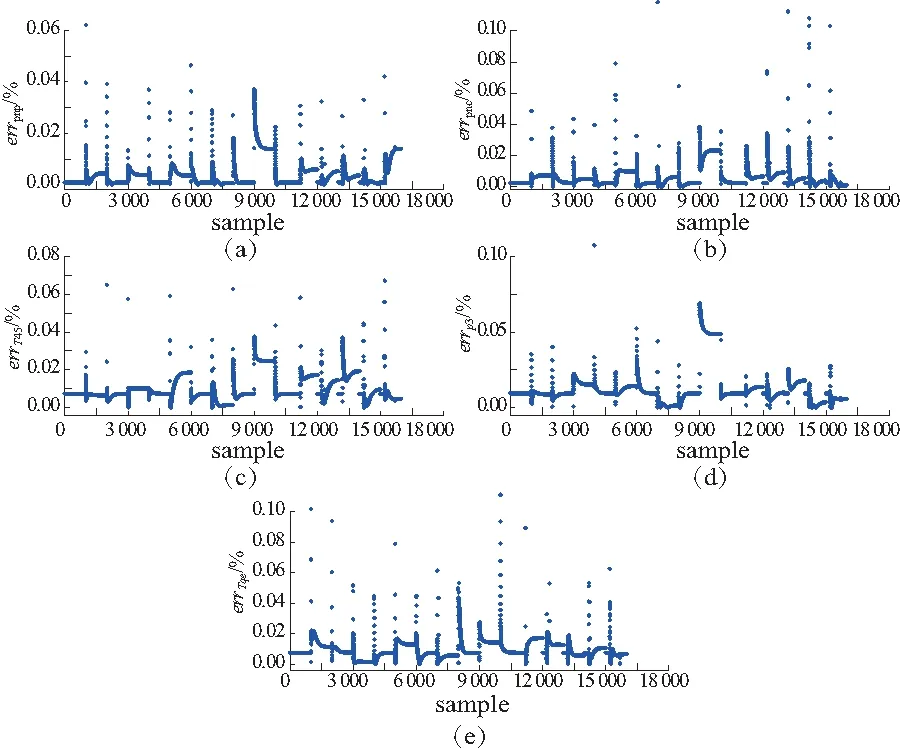
圖2 機載模型相對測試誤差

接下來在典型飛行任務下進行基于動態逆的渦軸發動機自適應模型仿真測試，并與基于線性卡爾曼濾波器的自適應模型進行對比，結果如圖3所示。其中，直升機飛行高度H=200 m，前飛速度νx=12 m/s，旋翼總距為9°，t=10 s時，壓氣機、燃氣渦輪的效率同時退化1%。

由圖3(a)、圖3(b)可知，無論發動機是否工作于額定狀態，線性卡爾曼濾波器與基于動態逆的健康參數估計器均能實現對壓氣機、燃氣渦輪效率的實時估計，且穩態估計誤差保持一致。而如圖3(h)所示，采用線性卡爾曼濾波器估計發動機健康參數時，單步耗時基本大于基于動態逆的健康參數估計器，后者可使總時間消耗有效減小26.2%((0.137 8-0.101 7)/0.137 8×100%)左右，在精度近乎一致的前提下，顯著提升了估計健康參數的實時性能。此外，由圖3(c)-圖3(g)可知，t<10 s時，渦軸發動機的健康參數均為0，發動機處于額定工作狀態，此時自適應模型的輸出結果與發動機的真實響應保持一致。而隨著發動機服役時間變久，雖然壓氣機、燃氣渦輪的效率發生退化，發動機處于非額定工況，工作狀態發生顯著變化。但基于線性卡爾曼濾波器與動態逆的渦軸發動機自適應模型的輸出參數仍可很好地跟蹤真實發動機的輸出響應，且穩態誤差均不超過0.5%。相比于前者，結合動態逆與神經網絡的渦軸發動機自適應模型動態精度更高，變狀態魯棒性能更加優越。

圖3 機載自適應模型仿真結果

3 結語

本文進行了基于動態逆的渦軸發動機自適應建模方法研究，提出并建立了綜合基于動態逆的健康參數估計器與基于神經網絡的渦軸發動機機載模型的自適應模型，并在典型飛行任務下，進行了仿真對比驗證，得到如下結論：

1)與線性卡爾曼濾波器相比，動態逆可在獲得相同健康參數穩態估計精度的前提下，單步耗時更短，總時間消耗可有效減小26%左右，實時性更高；

2)相比于線性卡爾曼濾波器，基于動態逆與神經網絡的渦軸發動機自適模型可實時跟蹤真實發動機的輸出響應，穩態誤差不超過0.5%，動態精度更高，更有利于實現渦軸發動機變狀態自適應跟隨。