基于小波的柴油機變速箱故障信號提取與處理
李建偉,楊洪海
(中國石油集團渤海鉆探工程有限公司第二固井分公司,天津 300280)
1 柴油機變速箱故障診斷技術發展概況
在固井施工中柴油機應用十分普遍,相關研究表明柴油機一般為非線性系統,其故障類型眾多且故障原因多種多樣。在柴油機的眾多子系統中,變速箱是極為重要的一部分,其工作狀態將直接影響柴油機系統能否正常運行。受材料、結構、運行環境等綜合影響,柴油機變速箱經常發生的故障形式有以下3 類。
(1)齒輪部分故障。這類故障又可以細分為齒輪面磨損、齒輪面擦傷與膠合、齒輪面解除疲勞、齒輪斷裂及彎曲疲勞等。在齒輪損傷初期,柴油機一般仍能運行,但隨著運行時間增長,齒輪將由磨損、擦傷等損傷逐步發展為斷齒,柴油機將無法正常工作。
(2)傳動軸部分故障。對于柴油機變速箱來說,傳動軸故障一般是因其自身強度變化而導致的傳動軸折斷或出現較大裂痕。在運行過程中,傳動軸一旦出現異常將導致極為嚴重的柴油機運行事故,輕則柴油機無法正常使用,嚴重時將會造成人員生命財產損失。
(3)滾動軸承造成的故障。軸承在長時間運行過程中會出現疲勞及磨損,其故障形式大多數為磨損、塑性形變、銹蝕、疲勞剝落、斷裂、膠合等。
2 小波分析理論
2.1 小波基確定
柴油機在運行過程中,可以通過測量設備測得柴油機的運行電流,但是僅從電流本身很難獲得故障的本質特征,因為電流包含著故障信息與很多不利于故障診斷和定位的噪聲、干擾信號。柴油機變速箱故障研究一般采用小波變換提取所需的故障分量,然而小波分析結果受小波基的種類、采樣率及分解尺度等因素的影響,如果不能選擇合適的小波基種類、采樣率以及分解尺度等參數就無法獲得準確地故障信號特征分析,最終將導致故障特征信號與實際信號特征相差甚遠。而SVD(Singular Value Decomposition,奇異值分解)通過對故障信號進行矩陣分解獲得故障信號奇異值子矩陣,而從信號奇異值中找出不同特性的奇異值點進行降噪和檢測分析。不同于小波變換、短時傅里葉變換等分析方法基于傅里葉變換基礎上,SVD 信號分析方法孤立于傅里葉變換思想,在信號降噪和特征提取方面具有顯著優勢,因此本文選取SVD 理論對所獲故障信號進行特征提取。
2.2 小波理論推導
作為應用數學中的良好分析理論,目前小波理論已經發展了幾十年時間,已經擁有相對成熟的分析理論體系。小波技術是對時間—頻率的聯合分析,能夠在圖像處理、信號處理這些難以分析的領域通過新的思路對相應的信號進行分解并提取其隱藏的特征。
常用的定理有兩個:
(1)設A∈Rm×n,ATA 的特征值的非負平方根稱作A 的奇異值。
(2)設A∈Rm×n,則必存在正交矩陣U=[u1,…,um]∈Rm×n和V=[v1,…,vm]∈Rm×n使得
這是矩陣A 的奇異值分解,通常簡稱為SVD,其中∑r=diag(σ1,…,σr),σ1>…>σr>0。
設離散數字信號X=[x(1),x(2),…,x(N)],則該信號通過X 構造Hankel 矩陣式如下:
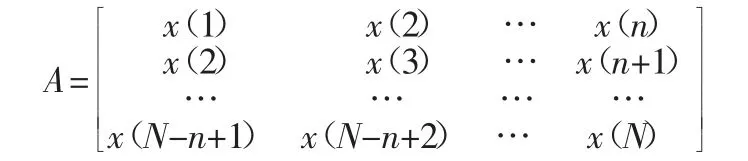
由于∑r是對角陣,因此SVD 可以將一個秩為r 的m×n 階矩陣A 表示為r 個秩為1 的m×n 階子矩陣的和。其中,每個子矩陣由2 個特征矢量(分別來自于U 和V)和權值相乘得到:
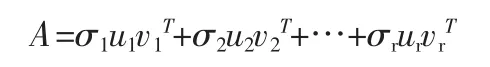
由SVD 理論可知ui之間是兩兩正交的,它們構成了m 維向量空間的規范正交基;vi也是兩兩正交的,它們構成了n 維向量空間的規范正交基。若令Ai=σiuiviT,則A∈Rm×n。設Ai中的第一個行向量為Ri,1,第n 個列向量為Qi,1則矩陣A 中第一個行向量X1,第n 個列向量In可分別表示為:
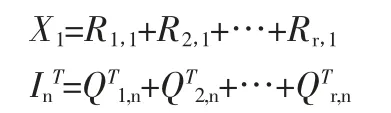
由Hankel 矩陣的構造過程可知,信號X 實際上由X1和InT拼接而成,若記向量Pi=(Pi,1,QTi,n),則信號X=P1+P2+…+Pr。
由此可見,被害人故意做出虛假陳述的行為,一方面會對現有的有限的司法資源造成不必要的浪費,另一方面也使得正在進行的刑事偵查與審判活動受到極大的干擾,使得司法公正的實現更加履步維艱。因此采用科學的思維方法對被害人的陳述進行系統全面的審查是必不可少的,而證偽思維便是這樣的方法。
由上式可以看出,當初始信號X 被分解后,其可以表示為一系列Pi信號的線性疊加,而這種疊加無論對哪一個分量信號進行剝除,也不會影響其他分量的相位,即其具有零相位偏移屬性。采用這種方式可以只提取對其中感興趣的分量信號,只對該信號進行降噪、分解、奇異值判斷,其結果將更加具有針對性和準確性。如果將定理中的m 取值為2,則通過X 構造的Hankel 矩陣可表示為:
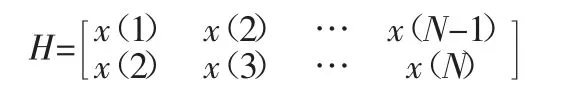
從上述公式中可以分析得出,經過SVD 分解將會得到2 個奇異值,而由于矩陣H 具有滯后性,因此奇異值σ1在初始信號中所占有的比重將遠遠大于第二個奇異值,其是初始信號的近似部分;相對應的奇異值σ2就是初始信號的細節部分。也就是說,經過SVD 分解后,初始信號即被分解為許多近似信號和細節信號的疊加。
2.3 小波SVD 適用性檢驗
圖1 為原始信號與經過二分遞推SVD 分解后的信號對比,可知經過SVD 處理后的故障信號具有更加明顯的奇異值波峰,同時可以明顯看到原始信號中被遮蓋的奇異值點,滿足本文研究的需求。

圖1 二分遞推SVD 信號對比
3 柴油機變速箱故障信號提取與處理應用實例
3.1 變速箱故障信號提取與降噪
在基于小波的柴油機變速箱故障信號提取中,噪聲信號對于故障信號奇異值的檢測具有非常大的影響,對于柴油機變速箱故障信號SVD 二分中,噪聲信號在近似信號和細節信號中都存在,而故障信號絕大部分都存在于近似信號中。也就是說,每進行一次SVD 分解將對噪聲信號進行減半處理,而對故障信號只削弱了很小一部分。但是最終將要使用的是初始信號的細節部分,所以SVD 二分在這種情況下無法對噪聲進行合理的去除,導致柴油機變速箱故障信號SVD 提取難以正常進行。因此在進行故障信號分析前,本文采用迭代SVD 對信號進行降噪處理,迭代SVD 降噪步驟可以分為:
(1)對含有噪聲的信號X 構造Hankel 矩陣H。
(2)對矩陣H 進行SVD 分解,得到對角矩陣∑r、左右正交矩陣U 和V。
(3)對分解得到的所有奇異值取平均得到δave。
(5)利用對角矩陣∑k和左右正交矩陣U、V 進行SVD 重構運算得到降噪后的矩陣H′,再恢復至降噪后信號X′。
(6)重復步驟(1)~(5),直至達到指定迭代次數即可獲得降噪后信號。
圖2 是原始信號與經過迭代SVD 降噪后的信號對比,可知原始信號中除首波外的少數奇異值點可以檢測,其余奇異值點幾乎淹沒在噪聲中;隨著迭代SVD 疊加次數的增加,奇異值檢測能力逐漸增強。
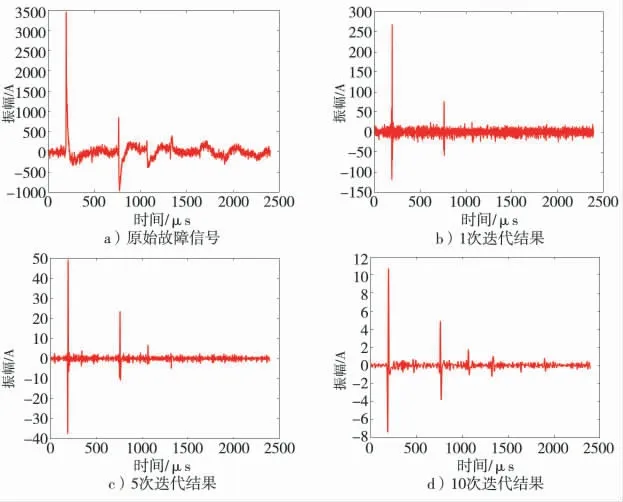
圖2 迭代SVD 信號對比
3.2 變速箱故障信號奇異特征部分提取
由于柴油機變速箱齒部、軸部以及傳動軸承部位的故障在故障信號高頻含量的多少有著明顯差別,故本文采用小波能量熵對故障信號在頻率上進行了能量分布分析。信號經過多分辨率分解后,每一尺度上對應的頻帶范圍:
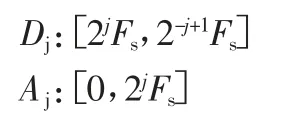
第j 尺度下的小波能量應為該尺度下重構信號的平方和:

本文采用db4 小波進行8 尺度分解,1 MHz 的采樣頻率,可劃分為9 個頻段,分別為1000~500 kHz、500~250 kHz、250~125 kHz、125~62 kHz、62~31 kHz、31~15 kHz、15~7 kHz、7~3 kHz、3~0 kHz。
圖3 給出了柴油機變速箱齒部、軸部以及傳動軸承部位故障在每個頻段上的能量分布規律,圖中分別用數字1~9 表示不同的頻段,1~8 為高頻段,9 為低頻段。傳動軸承往往造成的故障形式嚴重,故障信號的突變量大,暫態信號在高頻段能量占有比例較大,齒部故障信號能量則中在低頻段。
由圖3 可知,軸部分故障能量分布占比依次為0.8、1.8、11.69、8.11、7.85、3.36、5.89、0.6、59.9,齒輪部分故障能量分布占比依次為0.56、4.86、4.64、1.16、0.42、0.18、0.09、0.03、88.05,滾動軸承部分故障能量分布占比依次為0、0、0、0.01、0.01、0.05、0.06、0.14、99.73;滾動軸承部分故障與齒輪部分故障在能量分布上存在較大差異,提取故障信號在高低頻段的能量比p=
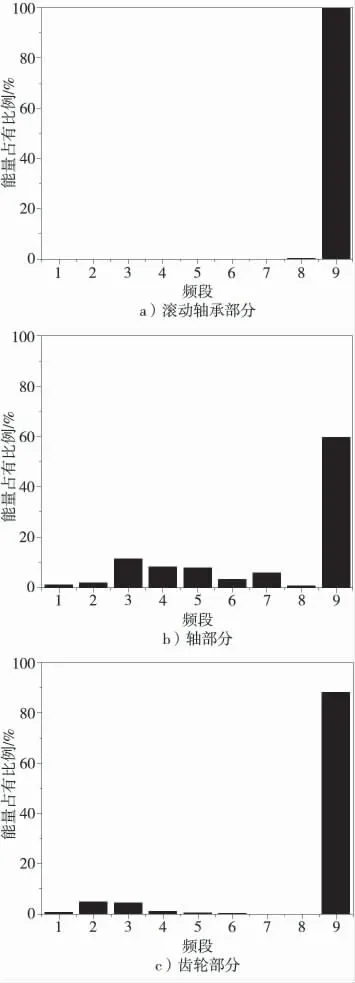
圖3 不同頻段能量分布
對上述故障信號進行計算,得到故障信號高低頻能量比p見表1。
由表1 可知,滾動軸承部分故障時,信號在高頻段和低頻段的能量均有一定占比,這是由于傳動軸承往往造成的故障形勢嚴重,故障信號的突變量大,暫態信號在高頻段能量占有比例較大,截波后又表現為短路特征,所以高低頻段能量比值較大;齒輪部分故障由微小損傷引起,信號能量主要集中在低頻段,高頻段能量比值相對較小。通過大量仿真結果計算得p=0.1,故齒輪部分故障與滾動軸承部分故障的判據為p<p0,判斷為齒輪部分故障,反之則判斷為滾動軸承部分故障。
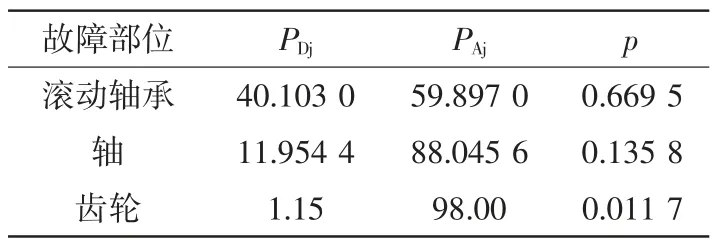
表1 高低頻能量比
4 結論
在現實固井工程中,由于其作業條件艱難,導致柴油機變速箱出現故障的因素眾多,因此急需基于小波技術對于柴油機變速箱故障信號進行提取、分析,以便迅速找出對應的故障類型。本文在針對其國內外的研究現狀進行分析的基礎上,給出柴油機變速箱故障診斷的發展趨勢,并采用更加細節的SVD 技術對于柴油機變速箱故障信號的時頻域特征進行分解、提取,最終得出柴油機變速箱故障診斷的具體結論。

