船用921A鋼高溫、高應變率下動態本構模型研究

吳海軍， 王可慧， 李 明， 段 建， 周 剛， 張慶明

(1. 北京理工大學 爆炸科學與技術國家重點實驗室，北京 100081;2. 西北核技術研究所，西安 710024)

921A鋼是我國自主研制成功的艦船用鋼，與美國HY系列高強度低合金鋼HY-80屬同一級別，具有良好的強韌性、工藝性以及耐海水腐蝕性，是我國重要的艦船結構鋼[1-2]。實戰中艦船面臨的主要威脅來自于反艦導彈，戰斗部撞擊、貫穿艦船結構鋼板的過程是一個非線性瞬態動力學問題，材料通常處于大變形、高溫、高應變率狀態。眾所周知，金屬材料在動態載荷作用下的力學性能與靜態時有較大差別，熱軟化效應也不容忽視[3]。

為了給艦船在動態載荷下的安全設計提供依據，許多學者對921A鋼的動態力學行為進行了研究。劉瑞堂等[4]對907A、921A[5]及945[6-7]艦船用鋼的動態斷裂韌性進行了試驗測試，首次獲得了相關材料的動態斷裂韌性數據。于兆斌等[8]測試了921A鋼在不同溫度下的動態斷裂韌性，發現其具有優良的低溫韌性，韌-脆轉變溫度為-100 ℃[9]。朱錫[10]首先采用分離式Hopkinson拉桿試驗對921A鋼在高應變率下的動態屈服強度進行了研究，發現921A鋼具有顯著的應變率效應。張林等[11]通過對稱碰撞研究了921鋼的動態損傷與破壞行為，得到了Hugoniot屈服極限以及層裂強度。李繼承等[12-13]結合試驗和數值模擬對921A鋼帽型試樣的絕熱剪切行為進行了分析。伍星星等[14]研究了921A鋼在拉伸、壓縮、扭轉斷裂過程中的應力狀態變化。

近年來，研究人員對921A鋼更高應變率范圍和高溫條件下的力學性能開展了進一步的研究。王子豪等[15]采用平板撞擊試驗測定了921A鋼極高應變率(～105s-1)下的動態屈服強度，當應變率大于1 000 s-1時，其動態屈服強度隨應變率增大而迅速增大，當應變率大于3 000 s-1時，動態屈服強度隨應變率增大變化緩慢。徐磊等[16]研究發現普通鋼材的高溫性能規范并不適用于921A鋼，將Johnson-Cook(J-C)模型中的溫度項與修正的Cowper-Symonds(C-S)模型直接相乘，建立了適用于火災爆炸的921A鋼本構模型。

隨著數值模擬手段應用日益廣泛和深入，迫切需要能夠描述921A鋼在高溫、高應變率作用下動態力學性能的本構模型參數。J-C模型包含了應變硬化、應變率強化和熱軟化三種因素對材料力學性能的影響，是模擬高速撞擊下金屬材料大變形問題較為理想的本構模型。本文對船用921A鋼高溫、高應變率下的動態力學性能進行了試驗研究，擬合得到了其J-C本構模型參數，并驗證了模型參數的可靠性，可為艦船結構防護設計和安全評估提供參考。

1 準靜態壓縮試驗

準靜態壓縮試驗采用CSS44100電子萬能試驗機進行，通過控制加載速率使應變率為0.001 s-1。準靜態壓縮試驗試樣為Φ5 mm×5 mm的圓柱。

電子萬能試驗機記錄的是載荷-位移(F-Δl)曲線，采用式(1)和式(2)可得材料真實應力-應變曲線。其中：A0為試樣初始橫截面積；l0為初始長度；σeng，εeng為工程應力、應變；σtrue，εtrue為真實應力、應變。圖1為921A鋼的準靜態壓縮真實應力-應變曲線。

(1)

(2)

從圖1中可以看出，921A鋼沒有明顯的屈服點，準靜態屈服強度約842 MPa。材料屈服后，強度隨應變的增加而增大，表現出較為明顯的應變硬化效應。

2 動態壓縮試驗

2.1 試驗原理

分離式Hopkinson壓桿(split Hopkinson pressure bar，SHPB)結構簡單，操作簡便，測量方法巧妙，加載波形易于控制，是測量高應變率(102～104s-1)材料力學性能最常用的試驗裝置。SHPB試驗的基本原理是：將短試樣置于兩根壓桿之間，通過子彈撞擊產生入射脈沖對試樣進行加載，如果壓桿保持彈性狀態，當入射桿中的應力脈沖到達與試樣的接觸面時，一部分入射脈沖被反射，在入射桿中形成反射波；另一部分則通過試樣透射入透射桿中，形成透射波；粘貼在入射桿和透射桿上的應變片能夠記錄反射波和透射波的波形。根據一維應力波理論[17]推導可得試樣的應力、應變和應變率

(3)

(4)

(5)

式中：εI，εR和εT分別為由應變片測量到的入射、反射和透射應變信號；A0，L0為試樣的初始橫截面積和長度；A，E，C分別為壓桿的橫截面積、彈性模量和彈性縱波波速。

2.2 試驗裝置

動態壓縮試驗采用西北工業大學SHPB試驗系統進行，如圖2所示。試驗應變率約為1 000 s-1、2 000 s-1、3 000 s-1、4 000 s-1，每個應變率包括室溫、300 ℃、500 ℃三個溫度條件(應變率4 000 s-1時只進行了室溫試驗)。高溫試驗中為了避免加載桿過熱導致的損壞及桿中溫度梯度過大而影響試驗的準確性，采用了同步組裝技術，具體工作原理見文獻[18-19]。動態壓縮試驗試樣也為Φ5 mm×5 mm的圓柱。

2.3 試驗結果及分析

圖3為動態壓縮試驗前后的試樣照片，試樣發生明顯的墩粗變形，呈鼓形。其中，室溫、應變率3 000 s-1情況下，應變值達到了0.70，而試樣未發生一般鋼材常見的剪切破壞，說明921A鋼在高應變率載荷作用下依然有很好的韌性，與普通高強鋼相比，可以依靠較大的變形吸收更多能量。

通過SHPB試驗，得到了921A鋼在室溫、300 ℃、500 ℃時，不同應變率下的動態壓縮應力-應變曲線，如圖4所示。從圖4中可以看出，與室溫、準靜態(～10-3s-1)時的應力-應變曲線相比，921A鋼表現出明顯的應變率強化效應和熱軟化效應。室溫、高應變率(～103s-1)條件下動態屈服強度較準靜態屈服強度顯著提高，而應變硬化效果基本消失；相同應變率(～103s-1)時，高溫(300 ℃、500 ℃)條件下的屈服強度較室溫時明顯降低。

2.3.1 應變率效應分析

圖5為不同溫度下，921A鋼屈服應力隨應變率的變化。由圖5中可以看出，雖然數據存在一定的波動，但總的趨勢是屈服應力隨應變率的增大而增大。室溫條件下，應變率4 000 s-1時921A鋼的屈服應力由準靜態時的842 MPa增加至1 203 MPa(增幅約43%)，較1 000 s-1時的1 093 MPa增加也有約110 MPa(增幅約10%)。300 ℃和500 ℃條件下，應變率由1 000 s-1增大至3 000 s-1，其屈服應力變化不大。

應變率敏感性因子β[20]定量表征了應變率對應變率效應的影響，可以近似地估計為屈服應力相對于應變率對數的斜率，即

(6)

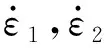
圖6為不同溫度下，921A鋼應變率敏感因子隨應變率的變化。從圖中可以看出，室溫時，應變率敏感因子隨應變率增大而增大；高溫時，應變率敏感因子明顯小于室溫時，且隨應變率增大變化不大。即高溫條件下，921A鋼的應變率強化效應弱于室溫條件，且對應變率的變化不敏感。

2.3.2 熱軟化效應分析

高溫條件下，克服位錯運動所需的能量較小，宏觀上表現為材料的塑性增強，屈服應力降低。圖7為921A鋼不同應變率時屈服應力隨溫度變化曲線。從圖7中可以看出，921A鋼表現出明顯的熱軟化效應，500 ℃時的屈服應力較室溫時大幅減小，較室溫時下降約400 MPa(降幅約48%)。同時可以看出，隨著溫度的升高，921A鋼的應變率強化效應逐漸減弱，500 ℃時，應變率1 000 s-1、2 000 s-1、3 000 s-1時的屈服應力變化不大。

溫度敏因子na定量表征了溫度對溫度效應的影響，可以近似地估計為屈服應力的自然對數相對于溫度自然對數的斜率，即

(7)

式中：σ1，σ2為不同溫度下的流動應力；T1，T2為相對應的溫度。

圖8為不同應變率下，921A鋼溫度敏感因子隨溫度的變化。從圖中可以看出，相同應變率條件下，溫度敏感因子基本不隨溫度變化；應變率2 000 s-1時的溫度敏感因子明顯大于應變率1 000 s-1時的溫度敏感因子。即較高應變率時，921A鋼的熱軟化效應強于較低應變率時，且對溫度的變化不敏感。

3 Johnson-Cook本構模型參數擬合

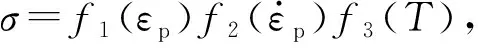
(8)

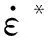
取參考應變率0.001 s-1，參考溫度298 K，921A鋼的熔點為1 765 K，擬合準靜態和動態試驗數據[22-23]，得到921A鋼的J-C本構模型參數，如表1所示。

表1 921A鋼的J-C本構模型參數Tab.1 The J-C constitutive model parameters of 921A steel

將921A鋼的J-C模型預測曲線與試驗應力-應變曲線進行對比，如圖9所示。可以看出，在試驗應變率和溫度范圍內，預測曲線與試驗曲線吻合較好，初步驗證了J-C模型參數的準確性。

4 動態沖擊試驗及數值仿真驗證

無論是準靜態壓縮還是SHPB試驗，都是一維應力應變狀態的簡單加載，模型對穿甲過程中靶板響應的模擬能力還有待進一步檢驗。為此，我們開展了彈體高速撞擊雙層921A鋼板的試驗，并采用得到的J-C本構模型參數對試驗現象進行了數值仿真。

4.1 彈體撞擊雙層921A鋼板試驗

試驗彈體長度為136.8 mm，直徑為72 mm，質量為1.65 kg。試驗靶板為雙層921A鋼板，厚度分別為6 mm+6 mm和8 mm+8 mm兩類，截面尺寸為600 mm×600 mm，兩層水平間隔600 mm，彈體前進方向與靶板法線方向成30°夾角。采用130 mm一級輕氣炮作為發射平臺，由于試驗彈外徑小于氣炮口徑，為次口徑發射，依靠尼龍彈托進行炮膛內彈丸的定位及推力的傳遞，彈丸撞靶前采用撞擊止退的方法進行脫殼。設計了專門的試驗靶架，起到固定靶板、預置傾角的作用，靶板后箱體內密實裝填木材對彈體進行軟回收。為保證試驗安全，靶架側面覆蓋防護鋼板，后面堆放混凝土防護靶，整個靶架置于氣炮試驗靶箱內。

彈體撞靶速度采用激光測速系統進行測試，其原理如圖13所示。預設的激光光束被飛行的彈體遮擋，測速系統通過記錄遮擋激光光束形成的時間間隔來計算彈速。試驗靶箱一側開有光學窗口，采用高速攝影系統，記錄彈體撞靶前飛行速度和姿態，如圖14所示。彈托在與脫殼器撞擊后完全碎裂，彈體保持水平方向運動，彈體與彈托碎片共同向前運動，直至撞擊靶板，如圖15所示。

4.2 靶板破壞仿真結果與試驗結果對比

考慮到問題的對稱性，建立1/2幾何模型，彈、靶均采用8節點三維實體單元，在對靶板進行網格剖分時，彈靶接觸區網格加密，距離彈靶接觸區較遠的地方逐漸稀疏，既能滿足數值模擬精度的要求，又能有效控制網格數量。彈體與靶板之間采用侵蝕接觸算法，對稱面施加對稱約束，靶板四周固支。

彈體對6 mm+6 mm雙層921A鋼板的撞擊速度為575 m/s。表2為靶板彈孔平均直徑試驗和仿真結果的對比，可以看出第一層靶板彈孔平均直徑的仿真值明顯小于試驗值，第二層靶板彈孔平均直徑的仿真值與試驗值吻合較好。圖16為靶板破壞形貌的對比。

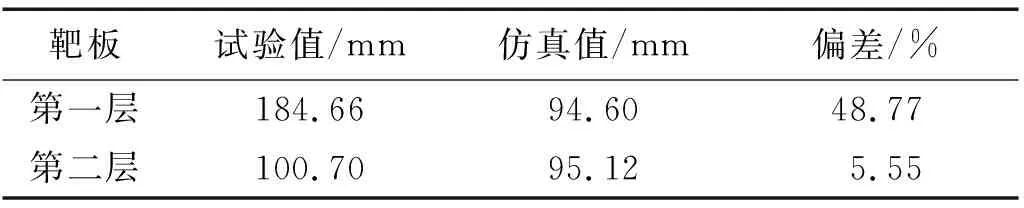
表2 6 mm+6 mm雙層921A鋼板彈孔平均直徑試驗與數值仿真結果Tab.2 Experimental and simulation results of average diameter of projectile holes of 6 mm+6 mm double-layer 921A steel plate

分析認為，彈體撞擊第一層靶板時，靶板因環向拉伸應力而形成“星形”裂紋，在裂紋擴展、花瓣形成的過程中，大量彈托碎塊隨之而來，以較高的速度撞擊靶板，彈托碎塊的動能轉化為靶板的變形能和裂紋擴展能，所以第一層靶板的塑性變形區域和裂紋擴展區域較數值仿真結果大得多。試驗后在第一層靶板前發現大量彈托碎塊，而第一、第二層靶板之間的彈托碎塊較少，也表明了這一分析的合理性。第二層靶板受彈托碎塊影響較小，所呈現的破壞模式較為典型，數值仿真結果與試驗結果非常相似。圖17為試驗中收集到最大的一塊靶板花瓣形碎塊，與數值仿真結果在形狀和變形特點上都基本一致。

彈體對8 mm+8 mm雙層921A鋼板的撞擊速度為484 m/s。本發試驗前采取措施對彈托碎片進行阻擋以減小其對靶板的撞擊效應，因此受彈托碎塊影響較小。數值仿真得到的靶板彈孔平均直徑和破壞形貌與試驗結果非常接近(見表3)，塑性變形區域和裂紋擴展區域基本一致，如圖18所示。彈孔上方被撕裂較大碎塊，在數值模擬結果中也有較好地體現，如圖19所示。

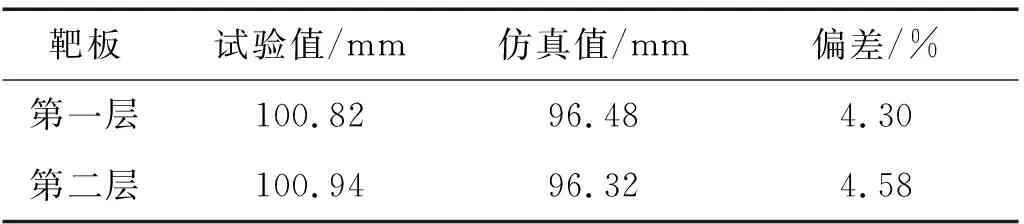
表3 8 mm+8 mm雙層921A鋼板彈孔平均直徑試驗與數值仿真結果Tab.3 Experimental and numerical simulation results of average diameter of projectile holes of 8 mm+8 mm double-layer 921A steel plates

5 結 論

本文基于準靜態壓縮和不同溫度、不同應變率的SHPB試驗結果，分析了溫度、應變率對921A鋼力學性能的影響，擬合得到了921A鋼的J-C本構模型參數，對比彈體高速撞擊雙層921A鋼板的動態沖擊試驗結果和數值仿真結果，得到的主要結論如下：

(1) 室溫、準靜態時，921A鋼沒有明顯的屈服點，材料屈服后，強度隨應變的增加而增大，表現出明顯的應變硬化效應。

(2) 高溫、高應變率時，921A鋼具有明顯的應變率強化效應和熱軟化效應，應變硬化效應基本消失；隨著溫度的升高，應變率強化效應逐漸減弱；熱軟化效應對應變率變化不敏感。

(3) 擬合得到的J-C本構模型能夠反映應變、應變率和溫度對921A鋼動態力學性能的影響，在試驗應變率和溫度范圍內，模型預測曲線與試驗應力-應變曲線吻合較好。

(4) 采用獲得的921A鋼J-C本構模型參數對彈體高速撞擊雙層921A鋼板試驗進行了數值仿真，靶板彈孔平均直徑和破壞形貌與試驗結果吻合較好，進一步驗證了模型參數能夠較好地描述921A鋼在高速沖擊條件下的動態力學行為。