問題驅動的協方差與相關系數的概念構建

陶 紅，徐耀坤，侯臣平

（國防科技大學 a.理學院；b.電子科學學院，湖南 長沙 410073）

引言

概率論與數理統計是一門研究隨機現象統計規律的學科，研究描述不確定性的數學模型和理論方法，可以應用于科學研究、工程實踐、經濟管理和人文社科等各個領域，是各大高校理工科專業的數學基礎課之一。作為隨機數學這一數學分支中學生所接觸到的第一門課，“概率論與數理統計”肩負著引導學生逐漸學會利用隨機性思維解決問題的重任。不同于以往的確定性數學課程，學生真正掌握概率統計的概念與思想具有一定難度。例如，很多學生難以完全理解條件概率、條件分布、協方差與相關系數等概念及其內涵。

數學概念反映了事物在數量關系、結構關系、空間形式等方面的本質屬性。數學概念教學要讓學生掌握概念的內涵和外延，理解概念間的邏輯關系。因此，數學概念教學應注重概念的構建過程，通過概念的構建過程，對學生進行思維訓練。讓學生在體會原理的過程中，不僅學會新概念，而且學會利用數學進行科學研究的思維方法。也就是說，數學概念教學不能僅滿足于讓學生接受、記憶、模仿和練習，更要教會學生自主探究，在自主探究的過程中發展智力、提高科學研究能力。

問題驅動教學模式以學生為主體，教師設置一系列問題，引導學生根據問題尋找解決方案，在解決問題的過程中達到教學目標。采用問題驅動的教學模式，有助于幫助學生了解數學概念的深刻內涵，培養數學思維方式，形成應用數學解決實際問題的能力。本文以協方差與相關系數為例，遵循問題驅動的教學原理，以“實例引入—提出問題—分析問題—解決問題”為主線，通過國內生產總值與軍費支出的關系分析實際案例，提出隨機變量關系描述的問題，并采用逆向推理得到協方差的定義。在此基礎上，進一步深化研究如何描述隨機變量關系的強弱及所研究的關系是何種關系，逐步構建協方差與相關系數的定義與內涵。

一、提出問題

為減少抽象感并激發學生的學習熱情，在課程開始時通過“國內生產總值與軍費支出的關系分析”這一實例提出問題：如何從數字特征的角度來描述兩個隨機變量之間的關系。具體地，我國2000—2013年國內生產總值（GDP）與軍費支出數據如表1所示。GDP與軍費支出均為隨機變量，不妨分別記為和，則（,）是二維隨機變量，（,）的幾何意義是平面上的隨機點。通過圖1（a）所示散點圖發現，14個樣本點散落在一條直線附近，隨著GDP逐年增長，軍費支出也逐年增長。可見，隨機變量與之間存在同向變化趨勢。從而結合本章主題提出問題：如何從數字特征的角度來描述兩個隨機變量之間的關系。

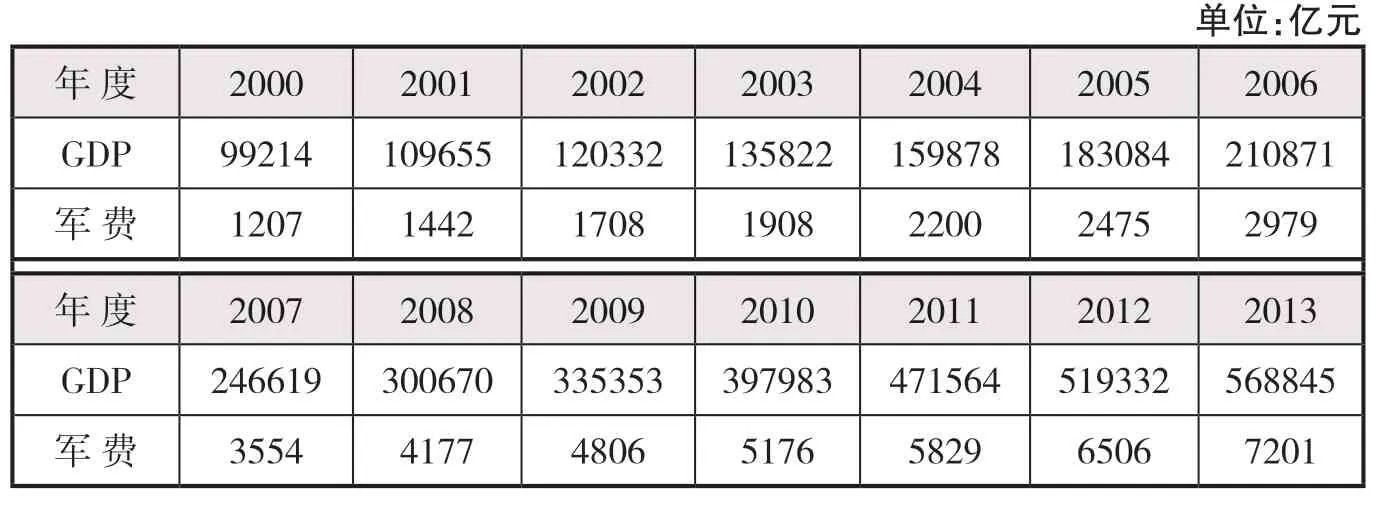
表1 我國2000—2013年GDP與軍費數據

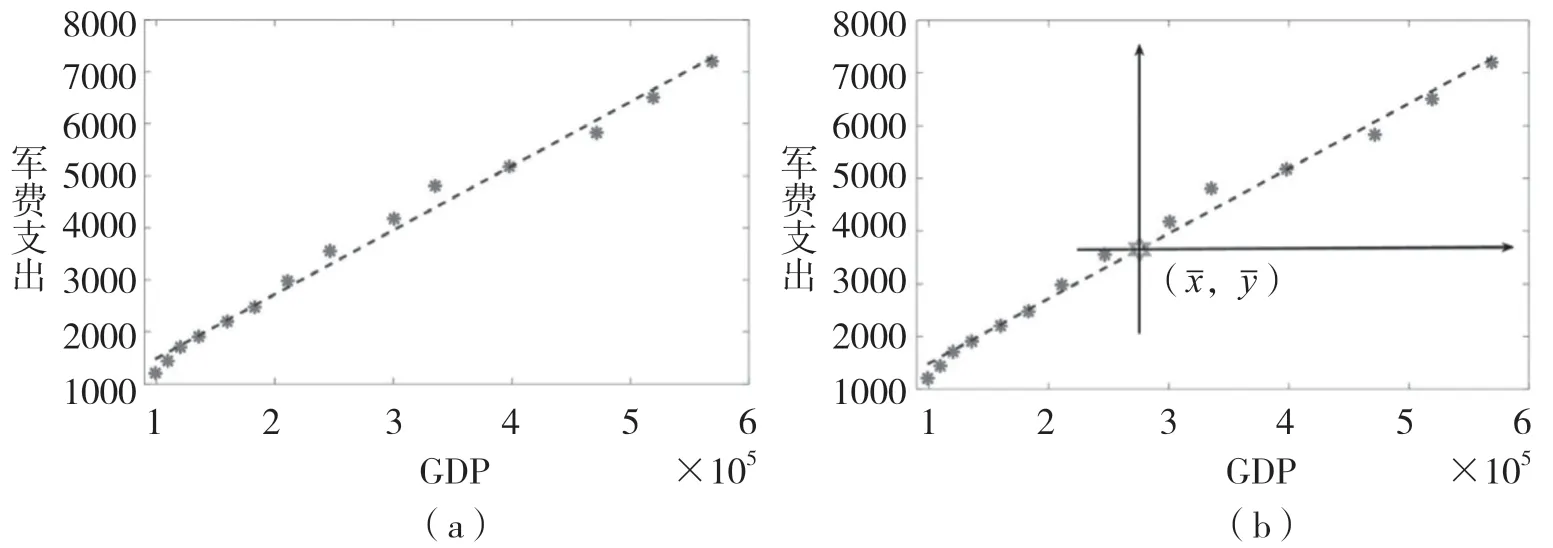
圖1 GDP與軍費支出散點圖

二、協方差概念引入

提出問題后，讓學生思考如何從數學形式角度進行描述。通過分析，問題轉變為找到一個依賴于,的數字量（,），滿足：（,）≠0，則表示,之間有關系。應如何找到滿足上述條件的數字量呢？通常學生難以從正面直接得到解決方案。于是基于逆向思維，引導學生從反面分析。如果存在一個數字量（,），滿足：當隨機變量,之間沒有關系時必有（,）=0，那么利用逆否命題則可以得到：當（,）≠0時，隨機變量,之間必有關系。由逆否命題的等價性，（,）所要滿足的條件轉換為“當隨機變量,之間沒有關系時必有（,）=0”。所謂沒有關系即相互獨立，由此引導學生回顧已經學習過的數學期望與方差在隨機變量相互獨立時所具有的性質。當,相互獨立時，有E（,）=E（）E（），D（+）=D（）+D（）。

如果令（,）=E（,）-E（）E（），（,）=D（+）-（D（）+D（）），那么（,）與（,）均滿足我們所提的要求。應該選擇哪一個呢？由于方差本質上是隨機變量函數的數學期望，而且計算比數學期望更復雜，因此優先選擇（,）。

更進一步，為了使定義更簡潔，如何將（,）=E（,）-E（）E（）寫成1項？如果寫成1項，其形式上必定是,的某個函數的數學期望，即需要把E（,）-E（）E（）變形為,的某個函數的數學期望。由于其中涉及的,交叉項的期望及各自期望的乘積，啟示我們變形為E{［-E（）］（-E（）］}，進一步驗證確實有E{［-E（）］（-E（）］}=E（,）-E（）E（）。

此時，詢問學生是不是完全得到了協方差的定義。為什么要問這個問題，協方差是利用數學期望定義的，而數學期望的存在需要滿足絕對收斂的條件，因此協方差存在的前提是E［-E（）］［-E（）］＜∞。由Cauchy-Schwarz不等式知，當,的方差都存在時，E［-E（）］（-E（）］＜∞成立。

定義1（協方差）：如果隨機變量,的方差都存在，那么稱Cov（,）=E{［-E（）］［-E（）］}為,的協方差。

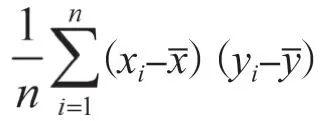
三、相關系數概念引入

當協方差的值非0時，則隨機變量之間存在關系。按照由淺到深的思路，接下來探討如何描述關系的強弱程度及是什么關系。向學生提問：協方差的大小能否用來度量關系的強弱程度，能夠反映關系強弱的數字量應具有哪些特點？為輔助思考，以GDP與軍費支出為例，讓學生計算單位分別為億元和億萬元時的樣本協方差。通過計算學生將發現兩種情況下的樣本協方差之間相差10倍，然而實質上GDP與軍費支出之間的關系并不會因金額單位的變化而變化。由此得出結論：協方差不能用于度量關系的強弱程度。事實上，由協方差的定義可驗證，對于常數,，Cov（,）=Cov（,）。顯然，協方差是一個受量綱影響的數字量。

于是，能夠反映關系強弱的數字量應具有不受量綱影響（條件1）的特點。除此之外，還應具有什么特點？提及強弱實質上是為了比較，因此數字量的取值應該是限定在一定范圍內（條件2），而且取值隨著關系的強弱單調變化（條件3）。

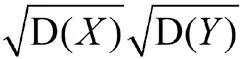
四、相關系數的意義

從構建相關系數定義的過程可知ρ不受量綱影響且取值在［-1,1］。但仍沒有揭示ρ的大小如何反映,何種關系的強弱。為此以常見的二維均勻分布與二維正態分布為例，利用Matlab動畫演示當上述兩個總體的相關系數從-1增加到1時樣本點散點圖的變化趨勢，以此來發現ρ的大小與,之間關系強弱的對應關系，并探索ρ描述的是,之間的何種關系。具體地，所采用的二維均勻分布與二維正態分布的概率密度函數分別為

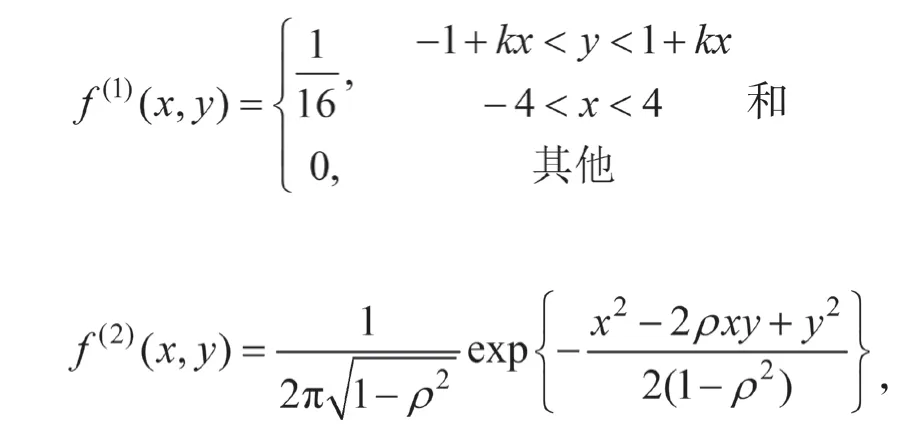
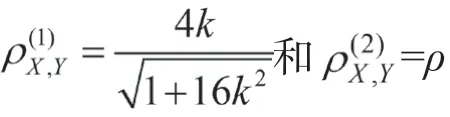
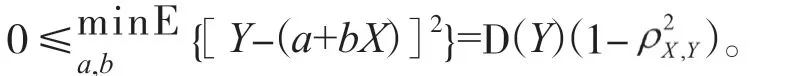
由此可得到如下結論：（1）|ρ|≤1。（2）|ρ|越大，則+與之間的均方誤差越小，即與之間的線性關系越強；反之，則與之間的線性關系越弱。并且，結合圖形（圖2）可知，當ρ＞0時，與整體上具有同向變化趨勢；當ρ＜0時，與整體上具有反向變化趨勢；當ρ=0時，與之間沒有線性關系，稱為與不相關。

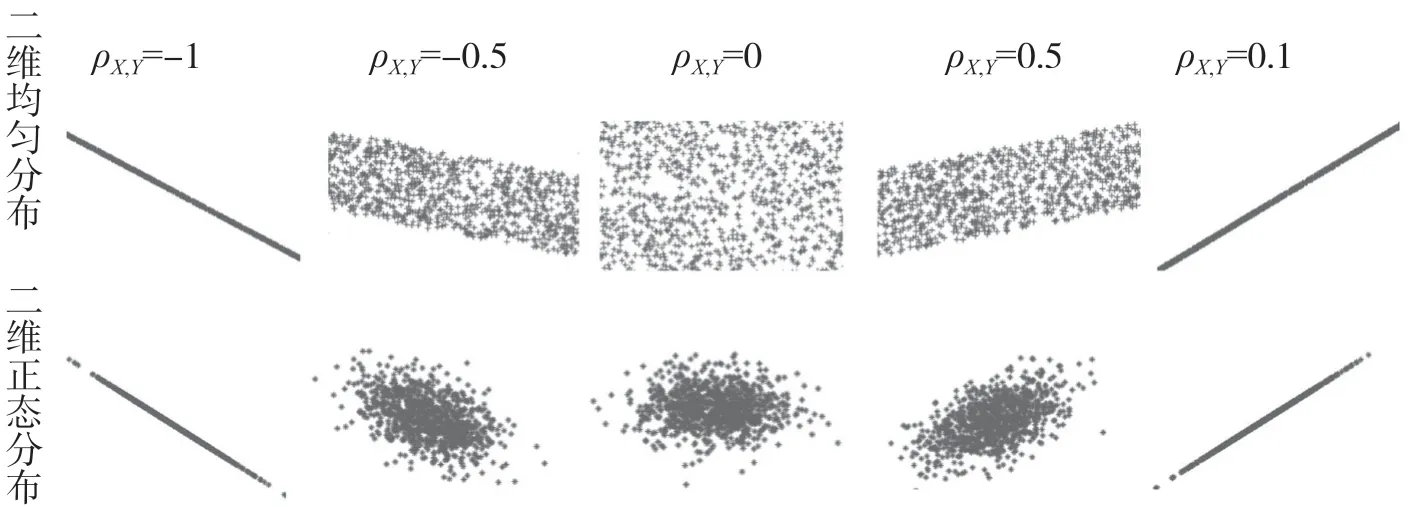
圖2 二維均勻分布和二維正態分布總體相關系數變化時樣本點的散點圖

結語

數學概念在數學課程中的基礎，為于課程體系的理解具有非常重要的作用。本文以概率論與數理統計中協方差與相關系數概念為例，遵循“以問題結構推進教學”的原理，圍繞隨機變量之間關系描述這一主題，提出一系列層層遞進、步步深入、具有內在邏輯聯系的問題，形成“問題—解決—問題—解決……”的問題導向結構教學過程，建構出協方差與相關系數的概念。在此過程中，引導學生探索、深究，有助于學生形成自主探究的思維模式和提升發現問題、分析問題和解決問題的能力。