經管類專業“運籌學”漸進式教學方法

陸 彪

（南京航空航天大學 經濟與管理學院，江蘇 南京 211106）

引言

“運籌學”是經濟管理類專業的重要基礎課程之一。運籌學致力于解決經濟管理領域的決策問題，通過采用定量方法，輔助管理者做出優化決策。運籌學涉及十幾個分支，如線性規劃、運輸問題、動態規劃、圖論與網絡計劃、決策分析、存儲論、排隊論等。各分支都有一套獨特的方法體系，各方法體系之間的關聯性較弱。從該角度而言，“運籌學”是一個內涵非常豐富的課程。對于經管專業的學生而言，學好運籌學，掌握其思想和方法，可以為從事經濟管理方面的工作或研究打下堅實基礎。

由于“運籌學”包含的分支眾多，而且各分支方法差異較大，因此學好運籌學并非易事。同時，各分支方法都要求建立和解析數學模型，而經管類學生數學功底較弱，這增加了他們學好該門課程的難度。因此，作為經管類專業運籌學授課教師，必須尋求有效的教學方法以引導學生學好該門課程。事實上，雖然運籌學中各分支方法差異較大，但它們都遵循同樣的底層邏輯：首先根據實際問題構建數學模型，然后解析模型的最優解，最后根據模型最優解確定問題的最佳方案。這三個環節逐步遞進、由淺入深、由易入難，這啟發我們采用一種漸進式的教學方法。

漸進式教學是一種應用較廣的教學模式。文獻調研顯示，漸進式教學在初中物理教學、微生物實驗教學、機械制圖課程教學、國際貿易專業課程教學及在外科門診臨床實習教學等各層次、各類型的教學中都實現了良好的效果。漸進式教學的核心思想是循序漸進地引導學生對課程進行學習，最終實現良好的教學效果。“運籌學”遵循著“問題建模—模型解析—最優解反饋”的邏輯，因此非常適合于采用漸進式教學方法。

本文旨在為經管類專業“運籌學”教學探索一種“建模—解析—反饋”的漸進式教學方法。首先分析“運籌學”教學中存在的問題，然后探索一種“建模—解析—反饋”的漸進式教學方法以應對存在的問題，從而實現經管類專業“運籌學”的教學目標。

一、“運籌學”教學中的問題分析

筆者近年來為經管類專業學生講授“運籌學”課程，通過觀察和交流，發現學生在運籌學的學習中還存在以下突出問題。

第一，學生對“運籌學”的學習興趣普遍不高。雖然“運籌學”對經管類專業學生是一門非常重要的課程，但在教學中發現很多學生沒有對“運籌學”表現出很強的興趣。通過與學生交流得知，很多學生感覺“運籌學”是一門偏數學的課程，與自己專業的關聯性不是很強。事實上，由于“運籌學”涉及大量的數學優化問題，在一些學院被劃歸在數學學科之下。對于經管類專業的學生偏重數學解析的“運籌學”，自然難以引起他們的興趣。因此，只有從實際管理問題出發引出數學模型，才能夠激發他們的學習興趣。

第二，學生對“運籌學”存在恐懼心理。“運籌學”模型解析以最優化理論作為基礎，其中涉及大量的數學推導和計算。經管類專業學生大多是文科生，數學基礎比較薄弱，很難輕易掌握其中的數學解析，從而產生恐懼心理。因此，在數學模型解析的教學中，教師需要傾注更多的心力，探索有效的方法，循循善誘。

第三，學生對模型最優解實際意義的認知不深。大多數學生在得到模型最優解后，通常不會去思考最優解的實際含義。模型最優解與實際問題最優方案之間存在一定距離，學生需要把最優解“翻譯”成最優方案，這樣可以幫助他們深入地認識“運籌學”。

為解決以上問題，在“運籌學”教學中應該首先以實際問題為牽引，講授數學模型的構建，其次探索有效方法以講授數學模型的解析，最后講授模型最優解對于實際問題的反饋，即采用一種“建模—解析—反饋”的漸進式教學方法。

二、“運籌學”漸進式教學方法

“運籌學”漸進式教學遵循“建模—解析—反饋”三個遞進的教學環節，如圖1所示。首先從實際問題出發，講授如何根據實際問題建立數學模型，其次講授如何解析數學模型獲得其最優解，最后講授如何將模型最優解反饋到實際問題以得到最優方案。

圖1 “運籌學”漸進式教學模式

（一）建模環節：從實際問題到數學模型

“運籌學”立足于解決實際問題。對于經管類專業的學生來說，只有讓他們意識到“運籌學”在解決實際問題中的價值，才能激發他們對“運籌學”的學習興趣。為此在每個分支教學伊始，選取一個實際問題作為引導案例。一方面引起學生對本分支的學習興趣，另一方面讓學生初步了解本分支將解決哪類問題。例如，在給經管類專業學生講授線性規劃時，筆者用某人力資源規劃問題作為引導案例；在講授運輸問題時，用某汽車公司的生產基地與分銷中心的運輸問題作為引導案例。從課堂情況來看，學生表現出很強的興趣。

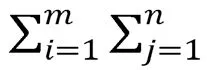
雖然不同的實際問題對應的數學模型不一樣，但它們都是由決策變量、目標函數和約束條件三部分組成。因此，在講授建模的過程中，著重培養學生的建模意識，以及正確定義決策變量和正確表示目標函數和約束條件的建模能力。

（二）解析環節：從數學模型到最優解

在建立數學模型之后，需要講授如何解析數學模型以得到其最優解，這是最難的，也是最重要的一個教學環節。實際上，每類數學模型都有對應的優化方法。例如，線性規劃模型對應單純形算法，運輸模型對應表上作業法，整數規劃模型對應分支定界法或割平面法，最短路模型對應Dijkstra 算法或Floyd-Warshall 算法。這些方法的共同特點是既有邏輯步驟，每個步驟下又有具體操作細節。例如，分支定界算法的邏輯步驟是對線性規劃問題進行反復的分支和定界，直至找到整數最優解，而如何分支和如何定界又是操作細節。

筆者在教學過程中發現，有些學生能夠掌握方法的邏輯步驟，卻在操作細節上不熟練；有些學生能夠較好地掌握細節，卻無法把握方法的整體邏輯步驟。因此，對于優化方法的教學應該使得學生既能把握方法的整體脈絡，又能掌握具體的操作細節。在此目標下，對于每種方法可以繪制一個方法流程圖，明晰該方法的整體邏輯步驟。例如，見單純形算法的流程圖圖2。在講解一種方法的過程中，采用該方法的流程圖作為引導。即按照流程圖一步一步地講授，講到每個步驟時跳到該步驟對應的操作細節進行詳細講解，講完該步驟下的具體操作之后再跳回到流程圖的下一步，依次往下，直至講完方法。通過此方法讓學生既能掌握方法的整體邏輯，又能掌握具體的操作細節。

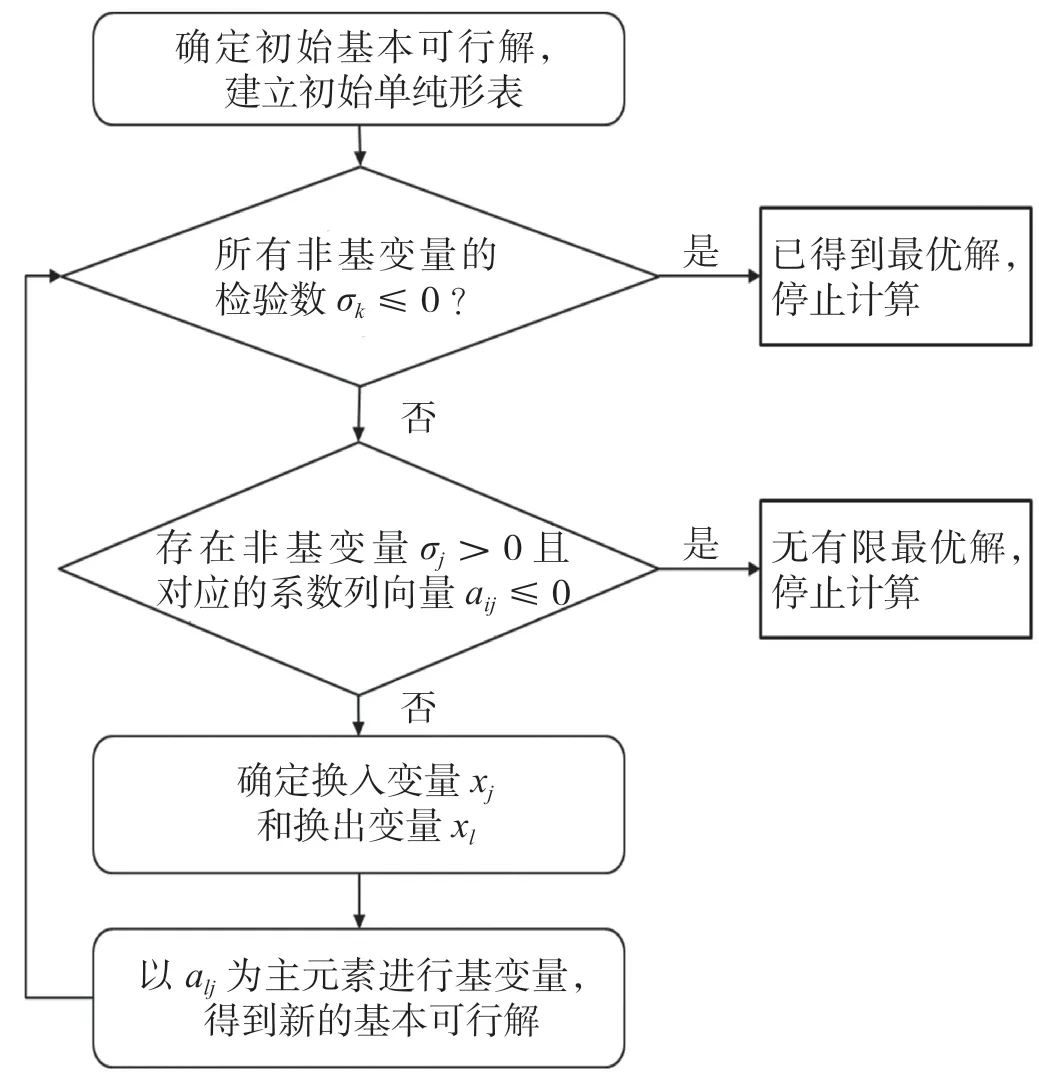
圖2 單純形算法流程圖

（三）反饋環節：從模型最優解到問題最優方案

在獲得模型最優解之后，需要將模型最優解反饋到實際問題，以獲得實際問題的最優方案，形成一個教學閉環。這是最容易的一個教學環節，但也是不可或缺的一個環節，否則就無法形成教學閉環。在這個教學環節中，需要教授學生將模型最優解“翻譯”成問題的最優方案。例如，生產計劃問題最優解為X=（10，20，25，0，0），其對應的最優生產方案為生產A產品10件，生產B產品20件，生產C產品25件。X的最后兩個分量等于0，表示松弛變量或人工變量取值為0，沒有實際含義。又例如，表1所示為某運輸問題的最優解。通過該最優解可知=5，=3，=1，=6，其余的x=0。根據該最優解，可得到最優運輸方案為：從產地A運往銷地B物資5個單位，從A運往B物資3個單位，從A運往B物資6個單位，其余產銷地之間則不進行物資運輸。注意到，雖然=1，但是由于B是虛擬的銷地，因此實際上A并沒有生產這1個單位物資，也就不會往B運輸物資了。通過最后的反饋環節，使學生加深對模型最優解實際意義的理解，也加深對于運籌學思想的理解，有利于夯實學生對于“運籌學”的學習興趣，進而提高運籌學的教學效率。

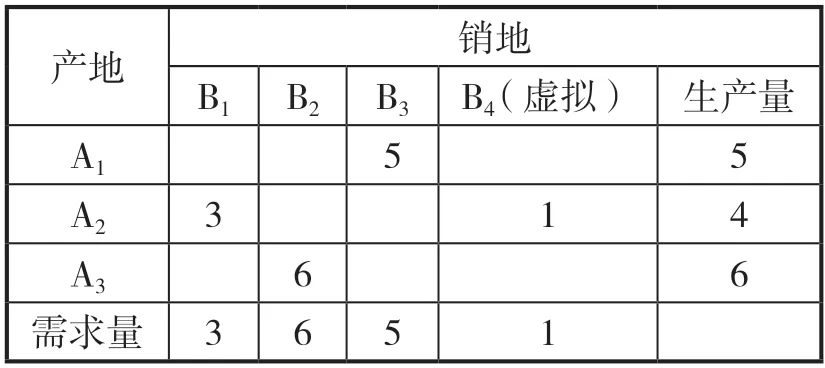
表1 某運輸問題的最優解

結語

本文為經管類專業“運籌學”課程教學提出了一種“建模—解析—反饋”漸進式教學方法。該教學方法將“運籌學”教學劃分為“數學建模”“模型解析”和“最優解反饋”三個環節。這三個環節層層遞進，首尾相連，形成一個教學閉環。建模環節著重培養學生對實際問題建立數學模型的能力，解析環節重點培養學生熟練掌握各種優化方法的邏輯脈絡和具體操作，而反饋環節則培養學生對于模型最優解實際意義的理解。通過該漸進式教學模式，激發學生學習“運籌學”的興趣，培養學生數學建模能力，引導學生掌握各種優化方法，夯實學生對“運籌學”的理解，最終實現“運籌學”的教學目標。

在實施該漸進式教學方法的過程中也會遇到諸多問題。例如，如何根據學生的專業背景選擇合適的實際問題，如何應對學生基礎和學習能力的個體差異問題，以及如何在優化方法講解中營造積極的學習氛圍等。這些問題需要在教學的過程中得到有效解決，才能夠保證該漸進式教學實現更好的效果。