基于邏輯回歸算法的某公司Offer申請結果預測研究

王祖斌，王 鑫

(蘭州職業技術學院 汽車工程與交通運輸系， 甘肅 蘭州 730070)

一、引言

我國改革開放以來，歷經40余年發展，在政治、經濟、國防、科技和民生等諸多領域都取得了舉世矚目的成就。國家的發展離不開科技，科技是推動現代社會發展的源動力。特別是近年來，國內科技公司如雨后春筍般遍地開花，其中不乏有很多國際知名企業，如華為、小米、騰訊、大疆和字節跳動等，在享譽海內外的同時也創造出一座座科技里程碑。這些公司為高級求職人才提供良好的晉升空間和廣闊的發展前景，進入這些企業工作是求職者實現人生價值的理想途徑之一。然而此類公司對人才的要求也比較嚴苛，在正式獲得公司offer之前，往往要通過幾輪考核，只有真正有實力的求職者才會被公司吸納。由于事關自身發展，廣大求職者通常會多手準備，在積極準備當前公司入職考核的同時，還會關注其他單位的招聘情況，以免耽誤自己就業。目標公司的offer申請是否成功是廣大求職者相當關切的問題。如何能夠較為準確地預測某公司offer的申請結果，及時調整自身求職計劃是具有一定應用價值的研究；從國家宏觀角度考慮，也可為調整高級人才就業相關政策提供數據參考。

在參考數據樣本特征變化的情況下，對事情的結果進行預測其實是典型的分類問題。解決此問題可以根據數據樣本的分布情況采用不同的方法，例如，當數據樣本是連續的，可以使用多重線性回歸[1]；如果數據樣本滿足二項分布，可以采用邏輯回歸[2]；若是Poisson分布則應該考慮Poisson回歸[3]；數據樣本是負二項分布，負二項回歸[4]則是較好的選擇等。目前利用邏輯回歸進行分類的應用研究很多，如在流行病學領域中就有不少相關的應用研究，可以利用邏輯回歸探索某種疾病的致病成因，根據不同的致病因素對某種疾病發生的概率進行預測。如郭志恒[5]等學者使用邏輯回歸等方法對腦卒中患者進行相關研究并構建腦卒中疾病的判斷算法,以便在疾病發生前提供一定的預警參考。段振云[6]等學者針對高精度零件圖像的亞像素邊緣提出了一種依靠邏輯回歸算法的邊緣定位方法，該方法有效地補償了由于光源強弱所導致的邊緣定位誤差等。邏輯回歸的應用已經較為廣泛，但用于預測申請公司offer是否成功的案例相對較為稀少。本文構建了一個邏輯回歸模型，該模型對目標公司offer申請的歷史考核數據進行學習后，便可以大致掌握考核成績與錄取結果間的相關規律，從而能夠較準確地通過新的考核數據來判斷某職位的申請結果，是一項可以落在實處的研究課題。

二、理論建構

(一)邏輯回歸(Logistic Regression)

在廣義線性模型(Generalized Linear Model)領域中，邏輯回歸與多重線性回歸[1]存在許多相似之處，它們最大的區別其實就在于因變量的不同，所以可以將這兩種回歸歸屬于同一個范疇。邏輯回歸模型的因變量既可以是二分類的，又能夠是多分類的，但在實際使用時，二分類的情況既比較常用又較易解釋，所以普遍使用邏輯回歸來解決二分類問題。邏輯回歸基本由以下幾個部分構成，它們也是實現邏輯回歸的幾個基本步驟，分別為：

1.預測函數

盡管邏輯回歸名稱中包含“回歸”二字，但如前所述，它其實是一種分類算法且主要用于解決二分類問題，可以用邏輯函數[7](也可稱為Sigmoid函數)，可以表示為：

(1)

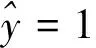
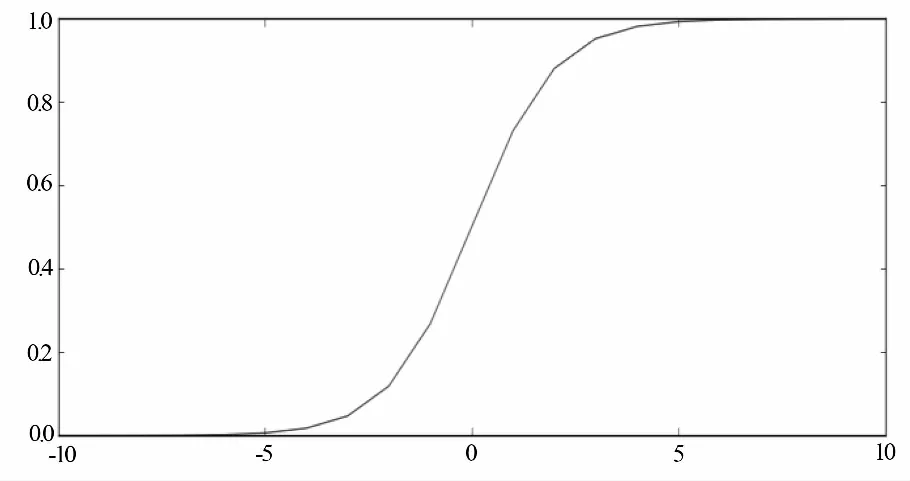
圖1 Sigmoid函數曲線

所有使得θT·x=0的點，形成一條決策邊界(Decision Boundary)[8]。例如當x含有兩個特征x1和x2時，則有θT·x=θ0+θ1x1+θ2x2=0為一條直線，它將所有數據樣本分割成兩個部分，是一條線性決策邊界。如圖2所示。

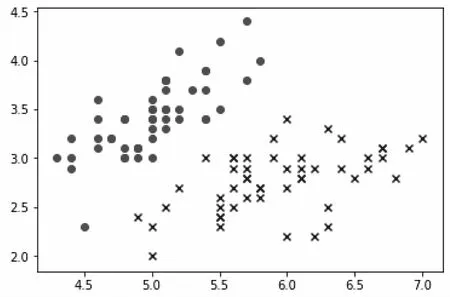
圖2 二分類數據樣本分布示例

其為鳶尾花數據集的樣本分布狀況，便可以利用線性決策邊界將其分割成兩個部分。如圖3所示。

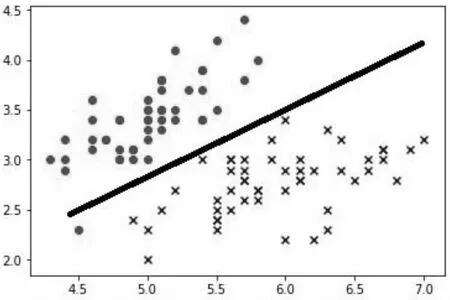
圖3 線性決策邊界

既然有線性決策邊界，那么也存在非線性決策邊界(Nonlinear Decision Boundary)，其主要用于分割數據分布比較復雜的數據樣本是非線性分布的情況，如圖4所示。

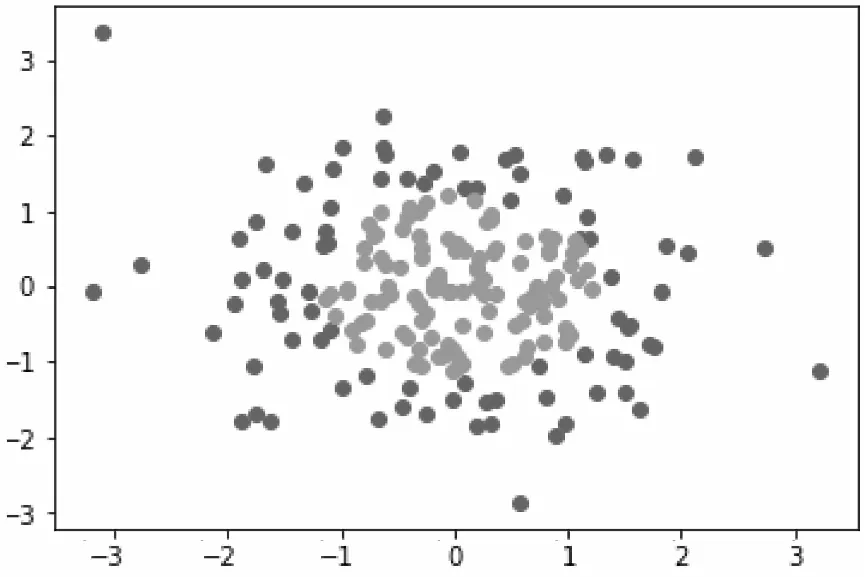
圖4 非線性數據分布散點圖

它是由隨機數生成的非線性分布形式的二分類數據。簡單歸納一下上述內容，對于線性決策邊界的情況，線性決策邊界可以用公式(2)表達如下：

(2)

根據(2)，可以構造預測函數g為：

(3)

其中，fθ(x)的取值為表達了預測結果為1的概率，由此可以推出當輸入為x時的分類結果分別為類別1與類別0的概率為：

(4)

2.損失函數

接上一小節，將公式(4)整合為：

p(y|x,θ)=(hθ(x))y(1-hθ(x))1-y

(5)

對(5)取似然函數為：

(6)

其中m表示m個預測結果，其對數似然函數則為：

(7)

根據最大似然估計[9]來求解使l(θ)取最大值時的θ，如果使用梯度上升法進行求解便會求得滿足需要的最優θ。若取

(8)

那么當J(θ)取到最小值時的θ則為滿足要求的最優參數。

(二)梯度下降法

上一節，在梯度下降[10]法中，J(θ)不斷趨向最小值的過程中，θ的更新過程可以用公式(9)表達：

(9)

簡化表示為：

(10)

三、預測模型

本文在邏輯回歸算法的基礎上，針對求職者在申請某公司offer過程中為了最大化自己的邊際機會，減少因為考核引起的求職成本，從而及時調整自己的就業規劃等問題，利用某公司offer申請的歷史數據，結合梯度下降法搭建了一個機器學習模型。該模型通過學習歷史數據所蘊含的普遍規律所產生的算法模型可以根據申請者給定的具體輸入數據樣本給出合理的預測結果，其工作流程簡述如下：

(一)通過兩個數據特征進行二分類結果預測的邏輯回歸架構

由于本文解決的實際問題是要根據輸入的數據特征給出申請某個offer成功與否的結果，該結果只有兩種，要么申請成功(可以用1表示)，要么申請失敗(可以用0表示)，而要解決二分類問題，邏輯回歸是比較有效的不二選擇。對于需要分析學習的歷史數據樣本而言，這些數據的特征無論是在使用邏輯回歸算法進行數據集學習的時候，還是面對隨機陌生數據樣本的時候，所要分析和處理的數據特征都是從數據文件中直接讀取的，而非類似從圖像數據樣本中通過專門的過濾器進行提取，所以并不需要構建復雜的特征提取裝置，也意味著其對于數據的處理并不需要巨大的計算開支，對于普通CPU來說已經能夠完成目標，相應地也使得將本文方法所構建的機器學習模型部署在智能手機這樣較為普及的弱算力設備上成為可能。本文針對具體的任務，根據公式(3)構建預測函數為：

(11)

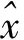
(二)運用梯度下降法更新η

對于本文研究對象，將公式(8)推廣至當前任務，則有：

(12)

其中m為2，實際上可以根據具體數據樣本的特征項數量來確定m的取值，如果所涉及的具體任務不同、數據集數據樣本的內容不同，可以因地制宜地繼續進行普適化推廣，這里不再贅述。求得當J(η)取得最小值時的η，這是一個不斷更新的過程，需要算法持續對導入的公司offer申請歷史數據進行學習，這個進程可以根據公式(10)表示為：

(13)

(三)實驗分析與評價

1.實驗環境

盡管本文用于實驗的機器已經搭載了較高算力的GPU，但考慮到用于學習的數據樣本僅含有兩個特征項且不需要進行特征提取等復雜運算，也為了驗證本文方法對于低算力設備的適應性，本文實驗在不使用GPU的情況下，僅依靠CPU實施了具體實驗。具體實驗環境配置情況為：CPU是Intel i5-8300h@2.3 GHz(8核)，內存8 G；操作系統采用Windows 10家庭中文版，Python 3.6開發環境，Jupyter NoteBook編輯器。

2.數據集

本文采用一個含有100個數據樣本的文本文件作為數據集，其中每一行具體數據樣本共同構成了整個微小規模數據集，作為本實驗的訓練數據集，每個數據樣本包含兩次考核成績的特征項與是否申請成功的標簽項。該數據集的具體結構及其包含的數據樣本容量圖5所示，其中顯示了讀取的前五個樣本的具體內容，從數據列維度上來講，前兩列是兩個具體的特征項，最后一列為標簽項。整個數據集可以看成是一個100行3列的二維矩陣。隨著研究的不斷深入，該數據集可以無限擴充。為了保證訓練效果，本文考慮了正、負樣本數量均衡的問題，所參與訓練的數據樣本大體分布是比較均衡的，可以用散點圖的形式將該數據集的分布情況較為直觀地表示出來，如圖6所示。

四、有效性驗證

首先建立要件模塊：(1)Sigmoid函數，它將輸出結果映射到預測概率。(2)自定義向量點乘Model模塊，它將返回輸出的預測結果。(3)Cost函數將根據權重參數計算損失。(4)定義Gradient模塊來計算各個權重的梯度方向。(5)定義Descent模塊對權重持續更新。在本文實驗中，根據比較迭代次數、損失以及梯度與閾值的差異采用了三種不同的梯度停止策略。在具體進行數據訓練之前，通過使用Shuffle進行了一定的數據增強，以使得本文方法具有更好的穩定性。

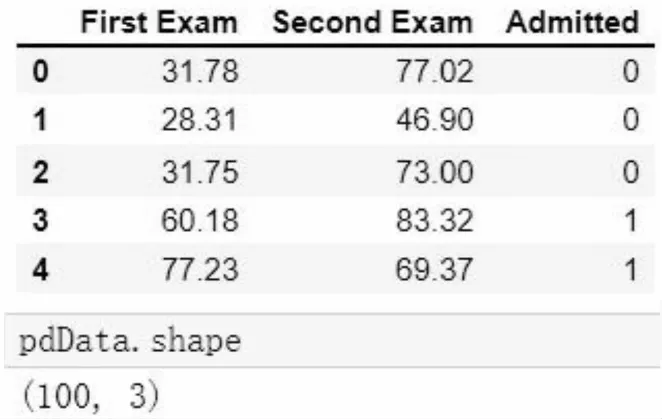
圖5 某公司offer申請歷史數據集

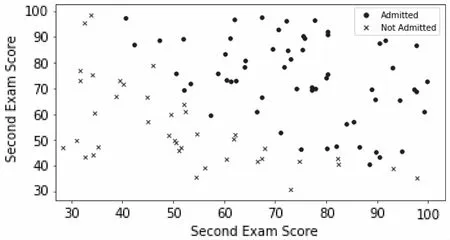
圖6 某公司offer申請歷史數據樣本分布圖

(一)根據迭代次數更新權重

對于所有數據樣本進行梯度下降訓練，那么Batchsize設為100。將迭代次數設為5000次，學習率設為0.000001。經過0.83s的訓練，權重更新完成，此時的模型損失為0.63，更新后的權重向量為array(-0.00027082，0.00715918，0.00367182)，效果比較差，如圖7所示。

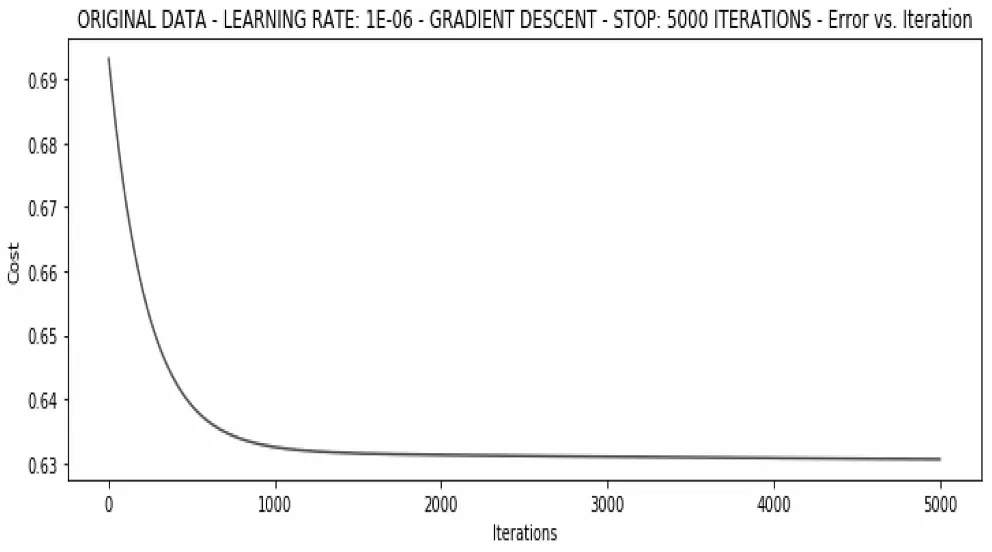
圖7 迭代5000次的訓練結果

(二)根據損失值更新權重

設定閾值為0.000001時, 經過112649次迭代，耗時18.17s后，得到權重向量為array(-5.25282519,0.04820083,0.0421662)，此時的損失已經大幅下降到了0.37，說明根據閾值更新權重的方式要明顯優于根據迭代次數更新權重的方式，該方式訓練結果如圖8所示。

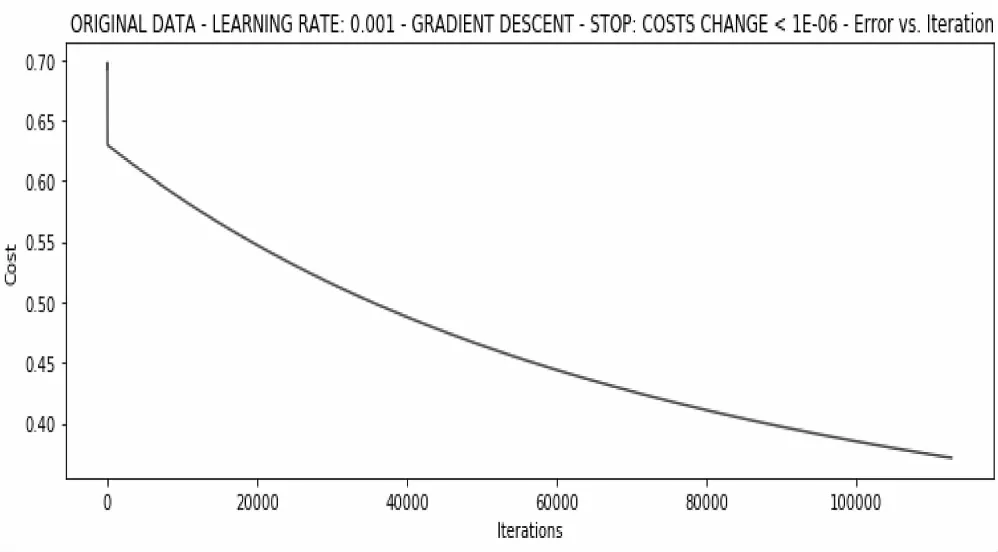
圖8 根據設定閾值的訓練結果

(三)根據梯度變化情況更新權重

當學習率為0.01且梯度小于0.05的情況下，算法才會停止訓練，在經過6.89s且40760次迭代后的訓練結果如圖9所示。

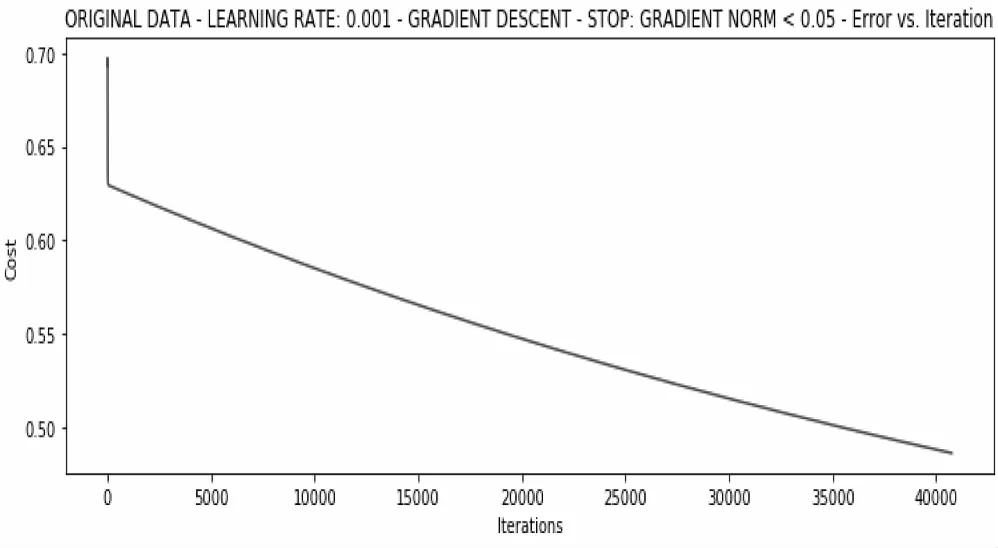
圖9 根據梯度變化的訓練結果

此時得到的權重向量為array(-2.40994356,0.02743917,0.01943823)，損失達到了0.49，效果不及根據損失值更新權重的方式，但該方式的訓練效率遠超根據損失值更新權重，耗時僅僅是根據損失值更新權重方式的三分之一。

(四)進一步探索實驗

在不使用數據增強的情況下，將學習率設定為0.001，采用隨機梯度下降法對原始數據直接進行5000輪迭代訓練，經過0.42s后，損失超過了1.59,效果很差，如圖10所示。

其訓練圖像波動非常嚴重，梯度已有爆炸的跡象，十分不穩定，說明數據增強是非常必要的。

繼續嘗試對數據進行標準化處理，將數據按其特征項減去其均值，再除以它的方差。最后對每個數據特征項而言，所有數據都將匯聚在0的鄰域范圍內且方差值為1，再次訓練在經過0.97s后停止更新權重，其結果如圖11所示。

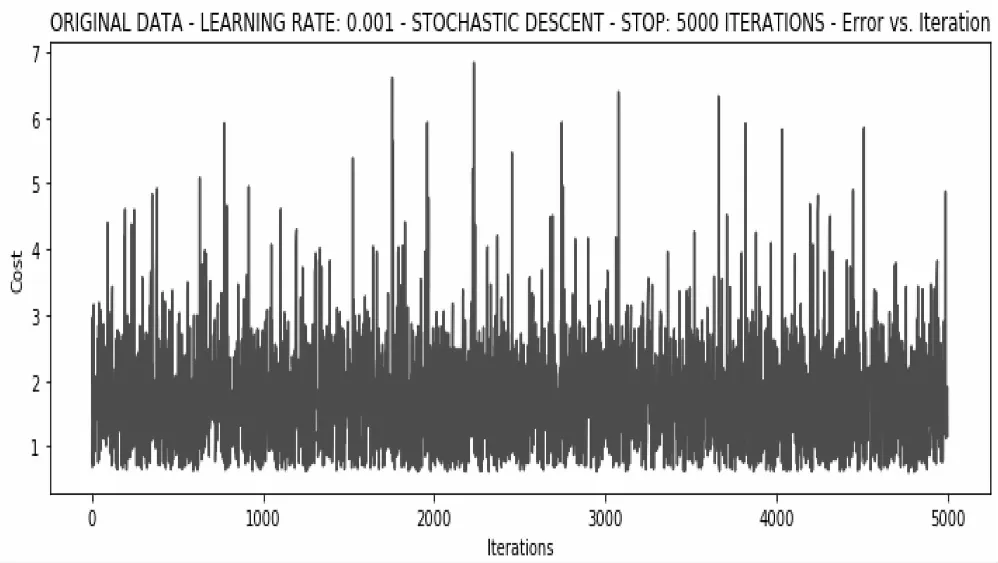
圖10 對原始數據的5000輪迭代訓練情況

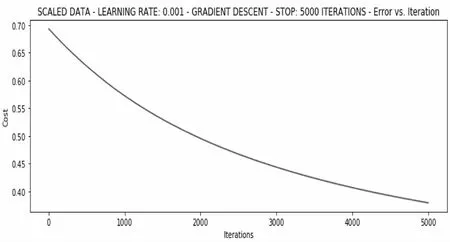
圖11 標準化數據的5000輪迭代訓練情況

算法損失已經大幅降至0.38。那么更多的迭代次數會產生的結果如何呢？繼續使用隨機梯度，學習率依然是0.001，在耗時4.05s并經過了67336次迭代訓練后，損失已經降至0.20，此時取得的權重向量為array ( 1.07426115，2.80678968，2.59430823)，如圖12所示。

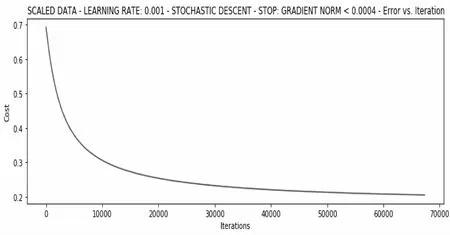
圖12 標準化數據的67336次迭代訓練情況

在對若干個測試數據樣本進行導入測試，可以得到的平均精度已經達到90%，已經滿足實際應用的需要，即本文最終確定采用融合了數據增強、數據標準化、邏輯回歸算法及隨機梯度下降法并在滿足梯度小于一個指定的微小閾值的情況下，經過充分數據訓練后所得到的模型是一個具有實際應用價值的文件模型。

五、結語

本文在邏輯回歸算法的基礎上構建了一個機器學習模型，該模型充分利用梯度下降法，通過對某公司職位申請的歷史數據進行充分學習，并達到了平均精度90%的測試效果。由于該類任務中的數據樣本特征顯著，也可以說特征一目了然，所以直接使用這些特征就可以完成數據訓練，也并不需要高算力設備支持，因此可以將該方法部署在類似于移動手機這樣的設備上，對于當下智能手機普及的時代而言，該方法針對某公司offer申請結果預測具有較好的實用價值。