基于CFD方法的矩形窄縫通道內過冷流動沸騰模型研究

劉 凱，李林峰，王明軍,*，章 靜，田文喜，秋穗正，蘇光輝

(1.西安交通大學 動力工程多相流國家重點實驗室，陜西 西安 710049；2.西安交通大學 核科學與技術學院，陜西 西安 710049)

板型燃料元件具有活性區比功率大、結構緊湊等優勢，在眾多研究堆、材料輻照堆中獲得了應用。其堆芯冷卻劑通道截面形狀為矩形窄縫，具有寬高比大的幾何特征，在發生過冷沸騰時，汽泡運動行為將受到高度方向上更陡峭的速度分布的影響而發生改變。

在加熱壁面上的汽泡行為中，汽泡滑移現象受到很多學者的關注。Thorncroft和Klausner[1]對豎直通道中冷卻劑FC-87的沸騰換熱系數進行了測量，結果表明，向上流動沸騰的換熱系數顯著高于向下流動工況，分析認為向上流動時壁面附近汽泡的滑移運動增強了換熱。Li等[2]進行了運行壓力0.1 MPa、高2 mm的窄矩形通道內豎直向上的流動沸騰實驗，同樣觀察到了頻繁的汽泡滑移。Yuan等[3-4]在運行壓力0.3～1 MPa工況的2 mm高窄縫通道實驗中觀察到了汽泡滑移現象，并對滑移汽泡的瞬態換熱項建模，結果表明滑移汽泡對換熱的貢獻可達靜止汽泡的10倍。Yoo等[5]使用熱成像記錄了滑移汽泡的影響面積，結果表明汽泡滑移過程中影響面積與汽泡直徑相關。

計算流體力學(CFD)目前已廣泛應用于工程模擬中[6-7]，包括棒束通道的兩相沸騰模擬[8-9]，但對窄矩形通道內沸騰分析時往往不能采用已有模型和關系式，因此，開發適用于矩形窄縫通道的沸騰模型具有相當的重要性。

本文針對矩形窄縫通道中的汽泡滑移對沸騰換熱的影響，構建包含滑移熱流的壁面熱流分配模型，并建立機理性的汽泡受力模型和滑移模型計算汽泡脫離直徑、浮升直徑和滑移距離等輔助參數，開發一套適用于矩形窄縫通道內豎直向上流動沸騰的壁面沸騰模型。選用Nuthel窄縫通道沸騰實驗進行數值模擬，通過對比壁面過熱度的計算結果與實驗結果，驗證本文模型對矩形通道內中低壓過冷沸騰流動換熱特性模擬的有效性。

1 數學物理模型

本文基于歐拉兩流體六方程模型，分別對氣、液兩相建立質量、動量、能量守恒方程，并考慮相間相互作用，引入相間質量、動量、能量交換模型[10]。相間動量交換中的作用力包括曳力和非曳力，非曳力又包含升力、湍流耗散力、壁面潤滑力，相間質量和能量交換包括近壁面沸騰換熱和相界面上的蒸發、冷凝過程。

此外，本文考慮汽泡滑移現象對沸騰換熱的影響，構建包括滑移熱流的壁面沸騰模型，并建立機理性的輔助模型計算相關汽泡關鍵參數，以對模型整體進行封閉，形成壁面熱流密度和壁面溫度的計算關系。

1.1 考慮汽泡滑移的壁面沸騰模型

Kurul和Podowski[11]提出的RPI壁面沸騰模型廣泛應用于流動沸騰計算，該模型僅考慮了汽化核心當地的汽泡行為，認為壁面熱流包括對流換熱、蒸發、淬滅熱流3部分。

本文針對窄矩形通道中的汽泡滑移行為，采用以下過程描述汽泡生長的周期，如圖1所示。汽泡在脫離汽化核心后將垂直于壁面浮升或平行于壁面滑移。滑移過程中由于其與壁面接觸處的微液膜蒸發，并與其他汽化核心處汽泡融合，汽泡直徑持續增大，當達到一定值后汽泡浮升進入主流區域。該過程中，汽泡離開汽化核心處、開始滑移時的直徑為脫離直徑dd，汽泡垂直壁面運動、遠離壁面并進入主流時的直徑為浮升直徑dl。

圖1 壁面沸騰模型對汽泡生長周期的描述Fig.1 Description of bubble period by wall boiling model

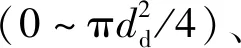
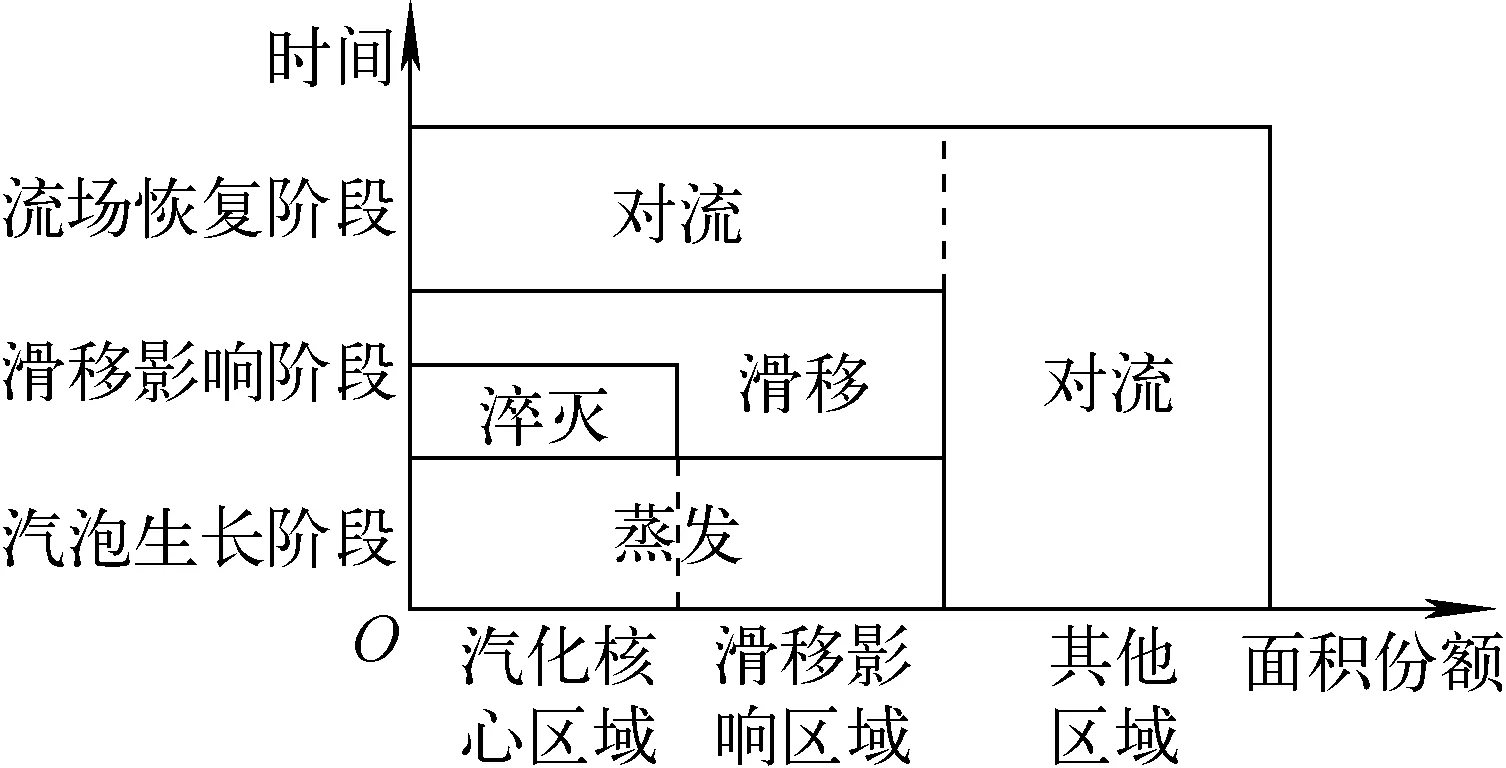
圖2 壁面沸騰模型對總熱流的分配Fig.2 Distribution of total heat flux by wall boiling model

1) 汽泡生長階段(0～tg，其中tg為汽泡生長時間)中，汽化核心區域的相變和滑移影響區域的微液層蒸發計入蒸發熱流。

2) 滑移影響階段(tg～t*，其中t*為換熱增強效果消失時刻)中，在汽化核心區域，固體側由淬滅熱流主導，而流體側為由于汽泡擾動的滑移熱流。在滑移影響區域，由汽泡滑移的擾動帶來的額外換熱增強計入滑移熱流。

3) 在流場恢復階段(t*～1/f，其中f為汽泡脫離頻率)中，單相對流換熱重新占據主導，而其他區域在整個汽泡周期中僅存在單相對流換熱過程。

據此，本文所開發的壁面沸騰模型將壁面總熱流qt分為4項熱流，分別為單相對流熱流qc、蒸發熱流qe、淬滅熱流qq和滑移熱流qs，其表達式為：

qt=qc+qe+qq+qs

(1)

蒸發熱流的表達式為：

(2)

式中：hfg為汽化潛熱；f為汽泡脫離頻率；N*為汽化核心密度。

由于汽泡滑移擾動，來自主流區域的較低溫度流體補充汽泡原先占據的位置，并與過熱壁面接觸換熱。將其簡化為半無限大區域冷卻平板瞬態導熱問題，則壁面瞬態熱流表達式為：

(3)

式中：kl為液相導熱系數；Tw為壁面溫度；Tl為流體溫度，此處取液相近壁面溫度；ηl為液相熱擴散率；τ為瞬態過程時間，即滑移熱流的影響時間，從汽泡滑移開始至換熱增強效果消失，即瞬態導熱系數與單相對流換熱系數相等時為止，記作0～τ*。令瞬態導熱系數與單相對流換熱系數相等，得到滑移影響時間表達式：

(4)

式中，hfc為當地流動恢復時的單相對流換熱系數。

考慮汽泡影響時間和影響面積，積分可得滑移過程中的瞬態導熱熱流，即滑移熱流：

(5)

式中，asl為汽泡的影響面積。

單相對流熱流根據近壁面對流換熱系數hfc計算：

qc=hfc(Tw-Tl)·(1-aslN*+aslN*(1-τ*f))

(6)

Gilman等[12]認為，汽泡生長時底部存在高溫干斑；當汽泡脫離后這部分壁面顯熱會釋放到流體中，組成新的淬滅熱流。具體地，認為汽泡底部干斑呈圓形，其直徑為汽泡脫離直徑的1/2。干斑下的半球形高溫區較其他區域溫度高ΔTh，淬滅點與周圍壁面的溫差約為3 K。因此淬滅熱流表達式為：

(7)

1.2 輔助模型

1) 汽泡受力模型

由于現有經驗關系的適用范圍有限或未區分汽泡脫離直徑和浮升直徑，本文建立汽泡受力模型計算汽泡脫離直徑和浮升直徑。采用Sugrue和Buongiorno[13]推薦使用的受力表達式和系數組合列于表1，其在反應堆典型應用場景內得到了一定的驗證。1個傾斜壁面上汽泡受力情況如圖3[13]所示，圖中x方向平行于壁面為流動方向，y方向垂直于壁面為浮升方向，θ為壁面水平傾角。

表1 汽泡所受作用力表達式Table 1 Expression for force acting on bubble

圖3 單個靜止汽泡受力示意圖Fig.3 Diagram of force on single static bubble

對于靜止汽泡，兩方向上的合力分別為：

(8)

式中：θ為加熱壁面的傾角；φ為汽泡偏向流動方向的傾角，一般假設汽泡生長方向與壁面法向的夾角為π/15。當ΣFx>0時，汽泡達到dd并平行于壁面運動；當ΣFy>0時，汽泡達到dl并垂直于壁面運動。

2) 汽泡滑移模型

通過滑移過程中汽泡生長方程計算汽泡滑移時間，進而得到汽泡滑移距離，本文使用Maity[14]擬合的汽泡直徑關系式計算，如下：

(9)

式中：d1和d2分別為汽泡滑移起始和終止時的直徑；τs為滑移時間；Jasup和Jasub分別為壁面過熱度和液相過冷度雅各比數；Reb為以汽泡平均直徑、汽泡滑移速度計算的雷諾數。

根據Basu[15]對滑移汽泡的建模，在汽泡由上一個汽化核心與當地汽泡融合并向下一個汽化核心滑移過程中，汽泡直徑由dN-1不斷增大，在該過程中判斷汽泡是否脫離即可得到汽泡滑移距離：

l=Nms+ldN-1～dl

(10)

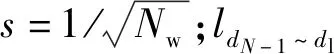
滑移過程中單個汽泡的影響面積為：

asl=l(dd+dl)/2

(11)

此外，當浮升直徑小于汽泡脫離直徑時，汽泡將不發生滑移而直接浮升。此時，汽泡行為實際上與RPI模型的描述相同，汽泡影響面積按下式計算：

(12)

式中，K為影響范圍因子。根據Valle和Kenning等[16]對汽化核心處汽泡的觀測分析使用以下公式計算：

(13)

3) 汽泡脫離頻率模型

汽泡脫離頻率使用Cole[17]關系式計算，其表達式如下：

(14)

式中，g為重力加速度。

4) 汽化核心密度模型

汽化核心密度使用Lemmert-Chawla[18]公式計算：

Nw=[n0(Tw-Tsat)]m

(15)

式中，參考密度n0和指數m分別取210和1.805。根據汽泡滑移距離，汽泡融合個數可以按l/s估計，則修正后的汽化核心密度為：

(16)

2 實驗模擬與結果分析

2.1 實驗介紹

選取西安交通大學反應堆熱工水力研究室(Nuthel)梁振輝[19]的過冷沸騰實驗進行模型驗證。實驗回路主要由屏蔽泵、穩壓器、預熱器、實驗段、直流加熱電源、冷卻器和相應的數據測量系統組成。實驗段為豎直放置的窄矩形通道，寬度為50 mm，高度為1.5 mm和2.5 mm。實驗段的加熱方式為電加熱，有效加熱長度為0.8 m。工質是去離子水，實驗壓力范圍0.5～5 MPa，入口過冷度范圍50～80 K，質量流量13.3～266.7 kg/(m2·s)，熱流密度范圍10～300 kW/m2。實驗段外壁面上點焊熱電偶，測量外壁溫度計算得到內壁溫度。焊點選擇在矩形壁面寬邊的中心線位置，布置間距為100 mm。實驗段參數列于表2[19]。本文選取截面尺寸為2.5 mm×5 mm通道內4組不同壓力下的實驗工況進行模擬，具體運行參數列于表3。

2.2 模擬方法

1) 計算區域選取

由于窄縫通道具有較大的寬高比，除接近邊緣處，在寬度方向上參數分布基本均勻。為降低計算量，通過選取通道中心的縱截面進行二維模擬的方法簡化。為驗證該簡化的合理性，對工況Nuthel-659分別進行三維和二維計算，計算條件保持一致。

三維與二維計算結果的對比如圖4所示，可見，二維與三維計算得到的中心縱截面上的壁面溫度計算結果相差不大；除邊角非加熱區域外，三維計算結果的空泡份額分布在寬度方向上分布均勻。因此采用通道中心縱截面進行二維模擬的簡化方法可行。

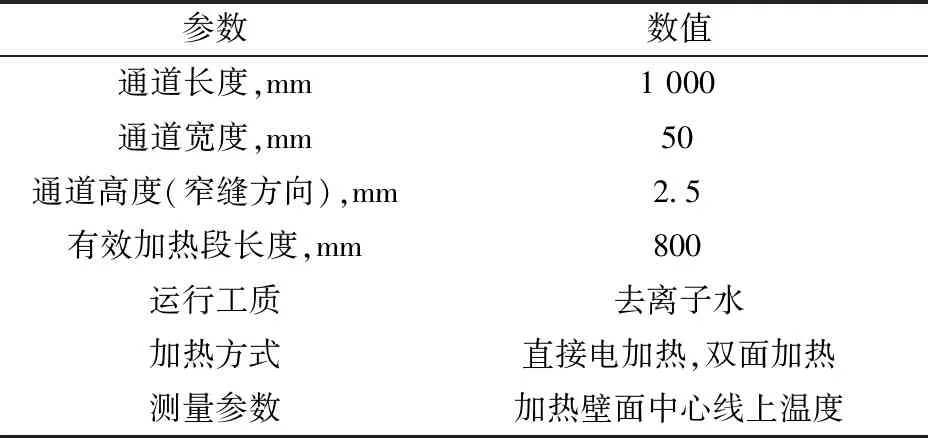
表2 Nuthel窄縫通道沸騰實驗段參數Table 2 Parameter of Nuthel narrow rectangular channel boiling experiment section

表3 模擬工況運行參數Table 3 Operating parameter of simulation case

a——壁面中心線溫度分布對比；b——三維模型出口處空泡份額分布圖4 二維模型有效性驗證Fig.4 Validation of 2D model

2) 網格劃分

使用四邊形結構化網格對矩形流道進行空間離散。為進行網格敏感性分析，劃分7套不同網格，具體劃分方式和計算結果列于表4，測試工況是Nuthel-627號。

對比網格#1、#2、#5和#7的結果可知，高度方向均勻劃分5個控制體時計算發散，將節點分布改為非均勻布置，使近壁面網格厚度為0.25 mm時則計算收斂；當劃分10或15個控制體時結果較為接近，但后者壁面網格y+值低于10，第1層節點落在速度過渡層內，不適用標準壁面函數。因此，計算中高度方向劃分10個控制體。對比網格#3～#7的結果可知，長度方向上網格數量對壁面過熱度影響較小。綜上，選取#3網格對Nuthel實驗進行模擬。

表4 網格敏感性分析Table 4 Grid sensitivity analysis

3) 材料物性

計算中使用運行壓力下的水物性。由于實驗中入口過冷度較高，因此液相物性使用入口溫度和飽和溫度兩點線性插值方法確定。過冷沸騰中氣相溫度幾乎維持在飽和溫度，因此氣相物性使用飽和狀態下的水蒸氣物性。

本文模型中的淬滅熱流考慮了壁面材料的影響，而兩實驗中沸騰區壁面材料均為鋼，因此取不銹鋼的物性典型值，密度8 000 kg/m3，比熱500 kJ/(kg·K)。

4) 邊界條件

入口邊界為流量入口，給定液相質量流量和溫度，氣相體積份額為0；出口為壓力出口，表壓為0。入口和出口非加熱段為絕熱邊界；認為加熱功率均勻分布，即加熱段為均勻熱流密度邊界。

2.3 計算結果分析

1) 壁面過熱度和近壁面空泡份額

分別使用本文模型和RPI模型進行模擬，得到壁面溫度和近壁面空泡份額的計算結果如圖5所示。

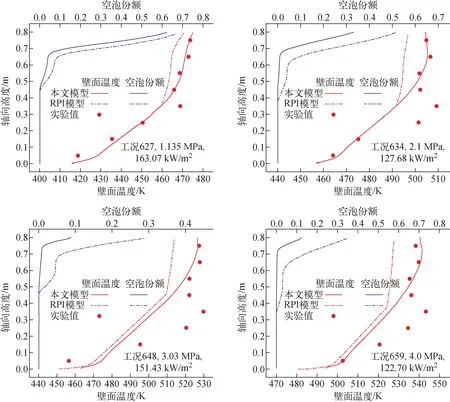
圖5 壁面溫度和近壁面空泡份額計算結果Fig.5 Calculation results of wall temperature and near-wall void fraction

由于過冷沸騰階段的高換熱效率，壁面溫度沿流動方向出現拐點，壁溫上升減緩，出現一段壁溫平臺，近壁面空泡份額相應上升。通道壁面自沸騰起始點的平均過熱度計算結果與實驗結果的對比列于表5，可見RPI模型的計算結果偏低，而本文模型計算得到的沸騰區過熱度與實驗值符合良好，對壁面過熱度的預測精度較高。此外，本文模型近壁面空泡份額的計算值較低。

單相對流區的壁溫計算結果存在較大偏差，導致沸騰起始點的預測不準確。分析認為偏差主要由熱效率不穩定造成：單相對流區的壁面溫度與壁面熱流密度約為線性關系，預先通過單相換熱實驗測量的熱效率可能在沸騰實驗過程中改變，因此模擬中的給定熱流與實驗條件存在偏差。而在過冷沸騰區域熱流偏差的影響較小，其原因為：過冷沸騰區壁面過熱度與壁面熱流約為0.25～0.3次冪函數關系，例如Jens-Lottes公式中ΔTsup∝q0.25，相同的熱流偏差在過冷沸騰區域引起的壁面過熱度誤差較小，僅為單相區域的2.4%。

2) 熱流密度分配

熱流密度分配的計算結果如圖6所示。本文模型的計算結果中，滑移熱流和單相對流熱流占據主導，蒸發熱流份額相對較小。而RPI模型的計算結果中，蒸發熱流在通道后段占據主導，單相對流熱流和淬滅熱流份額都相對較小。

表5 壁面平均過熱度計算結果與實驗結果的誤差Table 5 Error between calculated and experimental results of average superheat of wall

圖6 熱流密度分配計算結果Fig.6 Calculation result of wall heat flux distribution

本文模型的蒸發熱流份額較小，導致近壁面蒸發率較低，因此近壁面空泡份額的計算結果較小。此外，本文模型計算結果中淬滅熱流所占份額較小，幾乎可以忽略，說明在模擬工況中壁面顯熱的影響較低。

3 結論

本文針對矩形窄縫通道中的汽泡行為，考慮汽泡滑移現象對沸騰換熱的影響，構建了包含滑移熱流的壁面熱流分配模型，并建立機理性的汽泡受力模型和滑移模型計算汽泡脫離直徑、浮升直徑和滑移距離等輔助參數，開發了一套適用于矩形窄縫通道內向上流動沸騰的壁面沸騰模型，選用Nuthel窄縫通道沸騰實驗的1～4 MPa中低壓過冷沸騰工況進行驗證，主要結論如下：

1) 本文模型的壁面溫度計算結果相比RPI模型較高，模擬工況中沸騰區的壁面平均過熱度誤差由最大80%降至最大17%，說明滑移熱流的引入可以更精確地預測矩形窄縫通道內向上流動沸騰的壁面溫度；

2) 本文模型的熱流分配計算結果中，滑移熱流和單相對流熱流份額占據主導，蒸發熱流份額較低，蒸發率較低，因此近壁面空泡份額計算結果相比RPI模型較低；淬滅熱流所占份額較小，說明在模擬工況中壁面顯熱的影響較低。