熱管堆中分段式溫差發電器的仿真分析

張 胤，郭凱倫，王成龍,*，戴春輝，宋 蘋，張大林，秋穗正，田文喜，蘇光輝

(1.西安交通大學 核科學與技術學院，陜西 西安 710049；2.武漢第二船舶設計研究所 熱能動力技術重點實驗室，湖北 武漢 430205)

溫差發電器(TEG)能直接將熱能轉化為電能，因此TEG有著高可靠性、全固態、結構簡單及無噪音等優點，然而目前的TEG普遍存在著熱電轉換效率低下的缺點。使用高性能的熱電材料和優化幾何形狀是常用的解決辦法，除此之外使用分段式溫差發電器(STEG)也是一種不錯的解決辦法。STEG將不同溫度范圍中能取得最佳性能的熱電材料(2種或3種)拼接在一起，使用這種方法，STEG可在較寬的溫度范圍內取得更大的平均熱電轉換效率，這也使得STEG可在有著1 000 K溫差以上的熱管堆中作為能量轉換系統。

將TEG與核反應堆結合起來的設計在近十幾年越來越多。為了改進空間核動力系統，Markoliya等[1]將硅鍺TEG模塊與空間核反應堆結合起來，并提出了一種降低損耗、提高穩定性的方法。Wang等[2]設計了一種基于TEG的核電廠非能動冷卻系統，在該系統中，TEG用于將固有熱能轉換為電能。Gabbar等[3]評估了CANDU反應堆中TEG網絡的價值，并進行了相關優化。

然而，STEG在核反應堆中的應用，特別是在熱管堆中的應用卻鮮有研究。2004年，El-Genk等[4]提出了一種用于110 kW的熱管-分段式熱電模塊轉換器(HP-STMCs)的空間反應堆電源系統概念設計。該反應堆使用126根鋰熱管從堆芯獲取熱量，并使用STEG將熱量轉換為電能，轉換效率可達8.1%，反應堆的熱功率和裂變功率分別為1.641 MW和1.824 MW，分段式熱電模塊轉換器的熱側溫度恒定為1 300 K。

本文提出一種帶有STEG的熱管堆的新型概念設計。為分析STEG在熱管堆中的性能，建立相應的三維有限元模型。STEG的模型由兩種熱電材料組成，通過COMSOL軟件對STEG的幾何結構進行優化，并對其力學性能進行探索。

1 帶有STEG的熱管堆的概念設計

圖1示出帶有STEG的新型熱管堆的概念設計[5-6]。該熱管堆使用了Mo-14Re合金基體、控制棒、燃料棒、熱管、STEG和冷卻水板。如圖1所示，熱能自燃料棒中產生，隨后經由熱管傳遞至STEG。然后，部分熱能轉化為電能，剩余的熱能由冷卻水板帶走。與傳統的核反應堆冷卻系統相比，熱管有著許多優點[7]，如高固有安全性、非能動性以及高傳熱效率。與通常的核反應堆二回路相比，STEG能使反應堆更加緊湊、無噪音以及模塊化。

圖1 帶有STEG的熱管堆概念設計圖Fig.1 Schematic diagram of heat pipe cooled nuclear reactor with STEG

這種反應堆設計兼具了熱管和STEG的優點和缺點，這也意味著許多方面需要去探索研究。在經典的熱管堆kilopower中，堆芯溫度往往超過800 K，而熱阱一般為常溫冷卻水，這對于STEG而言，承載如此高的溫差是一項艱巨的挑戰，因此需使用有限元方法進行STEG的數值模擬，以找到最合適的幾何結構和最佳的熱電性能。

1.1 STEG結構

STEG的幾何結構如圖2所示。STEG主要由陶瓷片、導流片、焊料層和熱電材料構成。STEG參數列于表1。圖2中：LP為P腿冷端的熱電材料高度；LN為N腿冷端的熱電材料高度；SP為P腿的截面積；SN為N腿的截面積。

圖2 STEG的幾何結構Fig.2 Structure of STEG

表1 STEG的詳細參數Table 1 Detailed dimension of STEG

當STEG的上下兩端陶瓷片出現溫差時，將STEG與外接負載組合成閉合電路后，由于塞貝克效應會有電流產生。這種發電過程還伴隨著珀耳帖效應、湯姆遜效應、焦耳效應和傅里葉效應。本文在COMSOL軟件中創建了如圖2所示的模型，并選擇了相應的熱電物理場進行仿真模擬。本文主要是以熱電轉換效率為導向，尋找最佳的幾何結構。

1.2 單通道模型

將STEG集成便可形成分段式溫差發電模塊(STEM)，將STEM與熱管組合進而形成1個單通道模型[8]，該模型由熱管、燃料棒、STEM、銅基體和集熱器構成。18對如圖2所示的STEG組成了如圖3所示的STEM。1根熱管和10個STEM組合成1個基本的單通道模型。本文使用COMSOL軟件對單通道模型建模，選擇了相應的熱電和熱力物理場，探究相應的性能。

圖3 帶有分段式溫差發電模塊的單通道模型Fig.3 Single channel model with segmented thermoelectric module

2 STEG的數值模擬模型

2.1 熱電模型的控制方程

STEG是一種利用塞貝克效應、珀耳帖效應和湯姆遜效應等物理效應實現電能和熱能相互轉換的器件[9]。當STEG兩端產生溫差后，熱能自高溫端傳遞至低溫端，由于塞貝克效應，進而有電勢產生。若STEG和負載形成閉合電路，在電流作用下，熱電支腿和電極之間的接觸面上產生珀耳帖熱，這會削弱了STEG的發電能力。熱電材料在電流和溫度梯度的共同作用下會產生焦耳熱和湯姆遜熱。此外，熱電材料可通過自然對流和輻射向環境散熱。

因此，STEG的內部熱分布由傅里葉傳導、焦耳熱、珀耳帖熱、湯姆遜熱和熱損失決定。STEG的電勢分布由流過熱電支腿的電流產生的電勢和塞貝克效應產生的電勢組成。

熱流的控制方程[9]可表示為：

(1)

(2)

結合熱電耦合本構方程：

(3)

(4)

從而得到了描述溫度和電勢分布以及熱電耦合效應的控制方程：

(5)

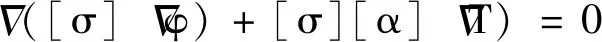
(6)

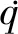
2.2 熱力模型控制方程

對于STEG而言，由于溫度梯度較大，熱應力是一個不容忽視的問題。熱應力會削弱器件的界面結合，導致缺陷、甚至失效[10]。熱力耦合分析需要確定應力-應變關系，并且需要考慮熱膨脹帶來的影響。

根據廣義胡克定律，在各向同性線彈性材料中，應力和應變相互獨立，并且相互疊加。剪切應變與泊松比有關，因此，本文得到以下應力-應變關系式：

(7)

式中：E為彈性模量；σ為法向應力；ν為泊松比；ε為應變。

法向應力與法向應變之間的3種關系為：

(8)

熱膨脹也會引起材料體積的變化。在各向同性材料中，體積膨脹系數是線性膨脹系數的3倍，因此熱膨脹引起的應力為：

(9)

式中：K為體積彈性模量；ε為體積應變；L0為初始長度。對于剪應力τ=Gγ，E=2G(1+ν)，G為剪切模量，γ為剪切應變。

綜合以上方程可得到最終的應力-應變方程：

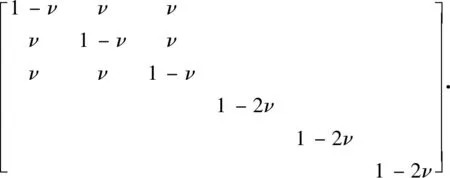
(10)

2.3 熱管計算模型

本文基于Zuo等[11]提出的熱阻網絡方法構建了熱管的數值仿真模型，如圖4所示。

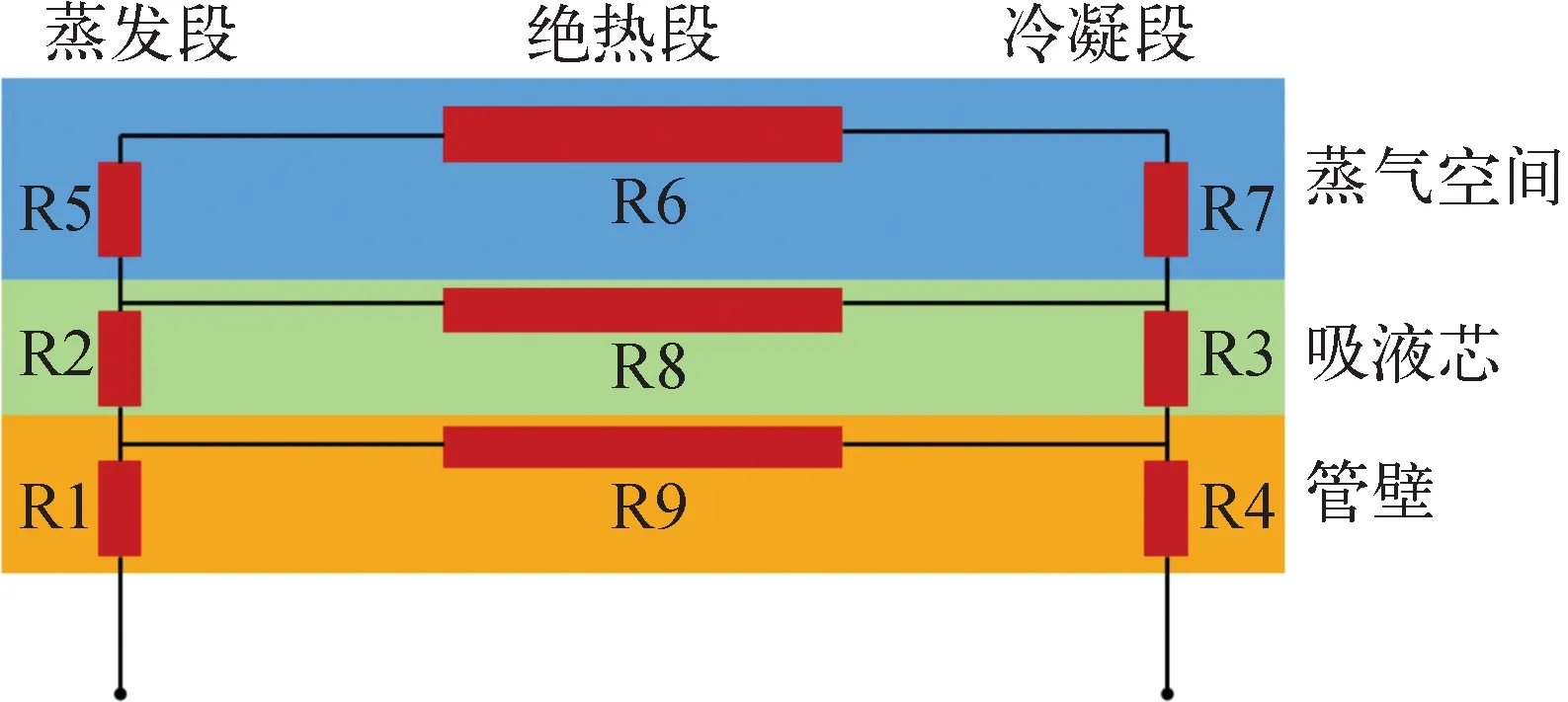
圖4 熱阻網絡模型Fig.4 Thermal resistance network model

熱管蒸發段管壁徑向導熱及其熱阻R1為：

(11)

式中：do為熱管管壁外直徑；di為熱管管壁內直徑；λw為熱管管壁材料的導熱率；L1為熱管蒸發段長度。

熱管蒸發段吸液芯徑向導熱及其熱阻R2為：

(12)

式中：dv為熱管內氣腔的直徑；λe為當量導熱系數，與吸液芯材料和工質的導熱性有關。

熱管冷凝段吸液芯徑向導熱及其熱阻R3為：

(13)

式中，L2為熱管冷凝段長度。

熱管蒸發段管壁徑向導熱及其熱阻R4為：

(14)

熱管蒸發段氣液界面的相變傳熱及其熱阻R5為：

(15)

式中：R為氣體常數；Tv為蒸氣溫度；r為汽化潛熱；pv為蒸氣壓力。

蒸氣軸向流動傳熱及其熱阻R6為：

(16)

式中：Le為熱管的有效長度；μv為蒸氣的動力學黏度系數；ρv為蒸氣密度。

熱管冷凝段氣液界面的相變傳熱及其熱阻R7為：

(17)

熱管吸液芯的軸向導熱及其熱阻R8為：

(18)

式中，L為熱管長度

熱管管壁的軸向導熱及其熱阻R9為：

(19)

2.4 材料屬性

STEG的導流片主要由銅構成，焊料層主要由Sn-Sb合金構成。STEG靠近熱端的熱電材料為方鈷礦，靠近冷端的熱電材料為碲化鉍。在本文的仿真模擬中，將陶瓷片和熱電材料視為脆性材料，將導流片和焊料層視為彈塑性材料。銅的極限強度、屈服強度和延展性分別為250 MPa、70 MPa和69%，焊料層相對應的值為41 MPa、26 MPa和38%。熱電材料的物性均來自文獻[12]。

2.5 邊界條件

為簡化計算，本文忽略了STEG不同材料之間的接觸電阻和接觸熱阻，同時忽略了表面自然循環和輻射換熱導致的熱損失，將與STEG相連的熱源和熱阱視為熱邊界條件。與P型和N型支腿相連的陶瓷片的上表面為熱源，并設置為固定溫度Th；將底部陶瓷片的下表面視為熱阱，并設置為固定溫度Tc；將連接到P腿冷端的電極電位設為0；將連接到N腿冷端的電路設置為可變電阻，以形成閉合回路。在熱應力的仿真模擬中，STEG的熱端上表面設置為固定約束。

圖5 STEG的網格Fig.5 Mesh of STEG

選用COMSOL軟件求解穩態工況下的有限元方程。圖5示出STEG的網格。本文使用熱電效應的多物理耦合模型來模擬STEG的熱電性能，并使用電磁加熱多物理耦合模型來解釋熱方程中的體積和表面損耗，本文也采用了熱膨脹多物理耦合模型來模擬溫度變化引起的熱應變。本次優化的目標首先需滿足熱電轉換效率最大化，其次滿足輸出功率最大化。仿真中一般考慮有5個獨立變量，但為簡化，將總熱電臂的高度(20 mm)和總截面積(8 mm×4 mm)設為了固定值，因此只考慮3個獨立變量，分別為P腿碲化鉍材料的高度、N腿碲化鉍材料的高度和PN腿截面積之比。

2.6 模型驗證

圖6示出COMSOL軟件模擬結果與文獻[12]結果的比較。隨著溫差的增大，模擬結果更接近于文獻[12]結果。當溫差超過400 K時，兩者的相對誤差小于3%。在680 K的溫差下，模擬結果表明熱電轉換效率為13.13%，文獻[12]的為13.09%。圖6表明，使用COMSOL軟件模擬高溫下的STEG是完全可行的。

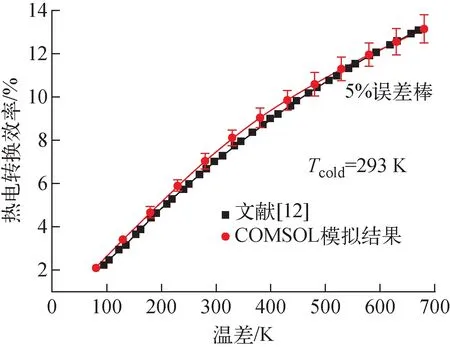
圖6 模型驗證Fig.6 Model validation

3 結果與討論

3.1 STEG的外接負載

圖7示出不同支腿長度下熱電轉換效率隨負載電阻的變化。如圖7所示，熱電轉換效率呈現出先增后減的趨勢，最大值出現在外部負載電阻為0.03～0.04 Ω區域。在以下研究中，本文均使用0.035 Ω的負載電阻進行模擬。

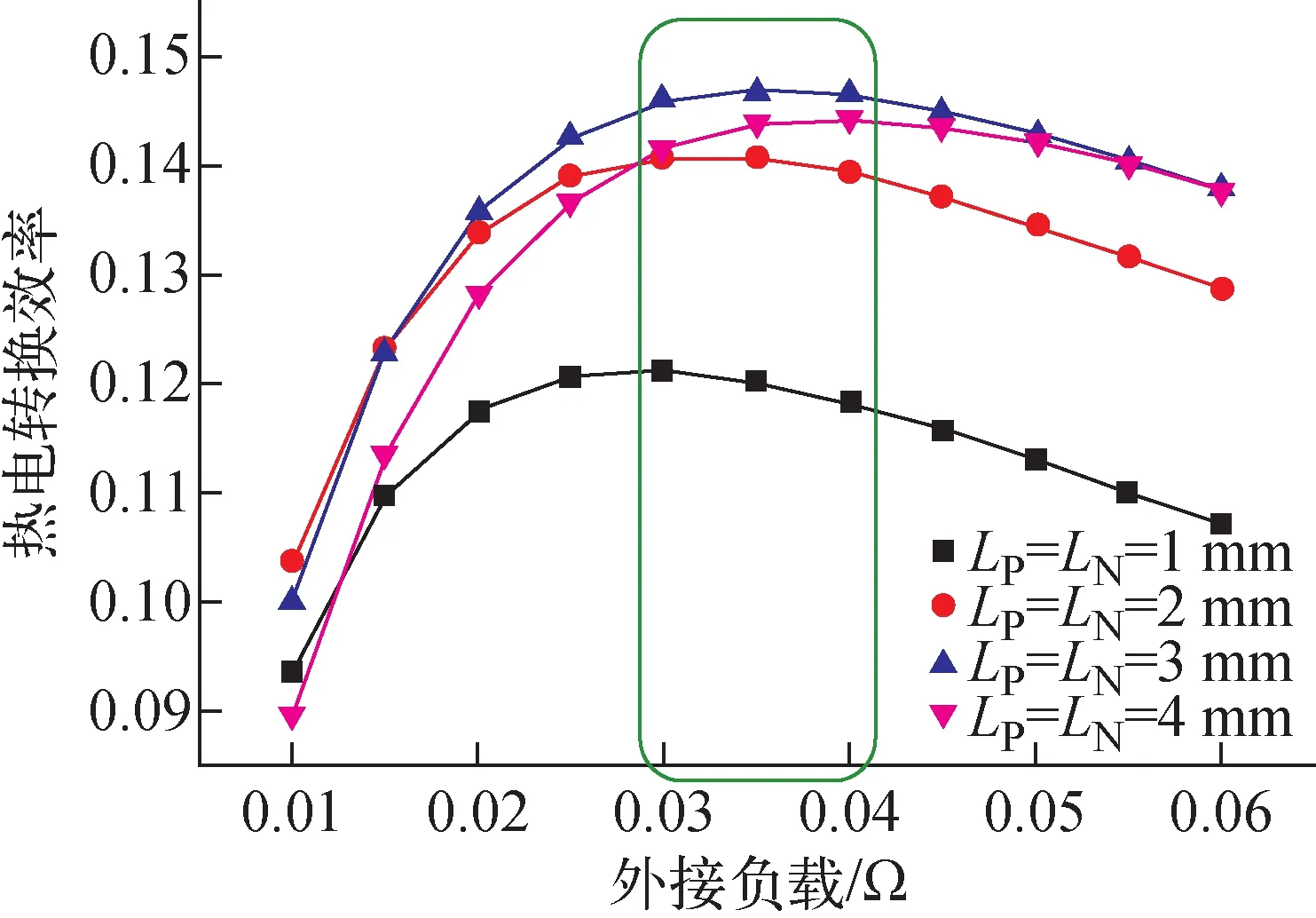
圖7 不同支腿長度下熱電轉換效率與負載電阻的關系Fig.7 Relationship between thermoelectric efficiency and external resistance under different leg lengths

3.2 STEG的優化設計

STEG的總體尺寸為：N型和P型支腿的總高度為20 mm，之間的間距為1 mm，PN腿的總截面積為32 mm2。為確定STEG的最優幾何形狀，還需對碲化鉍高度、方鈷礦高度和N型與P型支腿的截面積進行探究。

圖8示出P型支腿中碲化鉍高度對熱電轉換效率和輸出功率的影響。當碲化鉍高度從2 mm變為4 mm時，熱電轉換效率和輸出功率均先增大后減小，最大熱電轉換效率出現在3.1 mm高度，最大輸出功率出現在2.3 mm高度。在優化過程中，熱電效率最大值為13.966%，最小值為13.486%；最大和最小輸出功率分別為0.329 W和0.307 W。根據最高熱電轉換效率標準，P型支腿的碲化鉍高度為3.1 mm，相應的方鈷礦高度為16.9 mm，此時STEG的輸出功率為0.323 W，僅比最大值低0.006 W。

保持P型支腿的優化尺寸，圖9示出N型支腿中碲化鉍高度對熱電效率和輸出功率的影響。當P型支腿的碲化鉍高度從4 mm增加到6 mm時，熱電效率先升高后降低，最大熱電效率出現在4.7 mm的高度。輸出功率則一直在減小，最大值出現在4 mm高度處。在優化過程中，熱電效率的最大值為15.000%，最小值為14.908%，最大和最小輸出功率分別為0.372 W和0.361 W。根據最高熱電效率標準，N型支腿的碲化鉍高度為4.7 mm，相應的方鈷礦高度為15.3 mm，此時STEG的輸出功率為0.369 W，僅比最大值低0.003 W。

在截面積優化過程中，N型和P型支腿的尺寸保持了優化結果，圖10示出PN支腿的截面積比值SP/SN對熱電轉換效率和輸出功率的影響。當SP/SN從0.6變為1.7時，輸出功率先增大后減小，而熱電轉換效率一直在提高。SP/SN為1.35時，輸出功率達到最大值。在優化過程中，輸出功率最大值為0.374 W，最小值為0.335 W，最高和最低熱電轉換效率分別為15.75%和12.961%。根據最大輸出功率標準，P型支腿的截面積為4.6 mm×4 mm，對應的N型支腿截面積為3.4 mm×4 mm。

圖8 P型支腿中碲化鉍高度對熱電效率和輸出功率的影響Fig.8 Effect of bismuth telluride height in P-type leg length on thermoelectric efficiency and output power

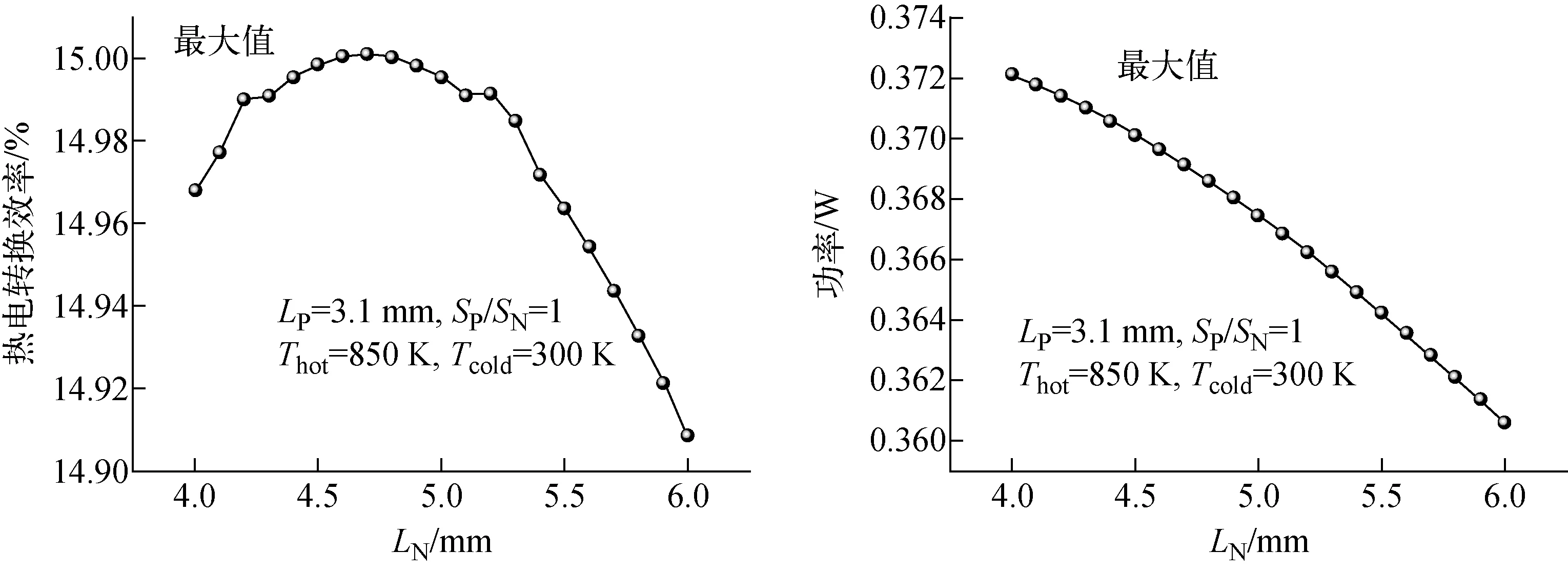
圖9 N型支腿中碲化鉍高度對熱電效率和輸出功率的影響Fig.9 Effect of bismuth telluride height in N-type leg length on thermoelectric efficiency and output power

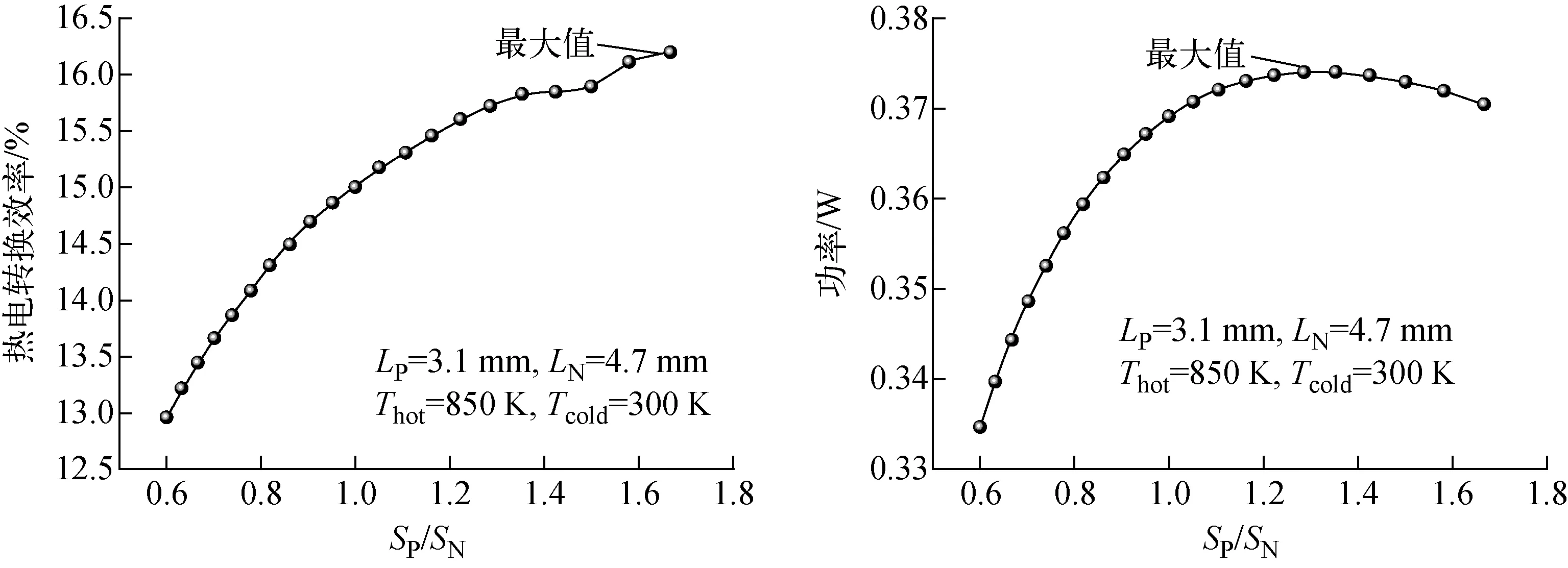
圖10 SP/SN對熱電轉換效率和輸出功率的影響Fig.10 Effect of SP/SN on thermoelectric efficiency and output power

3.3 STEG的熱力性能

STEG兩端的溫差超過800 K，如此巨大的溫差會帶來熱應力，進而導致器件破裂，因此有必要研究STEG的力學性能或熱應力極限。

圖11示出STEG中熱電材料的Von Mises應力分布。由圖11可見，碲化鉍、方鈷礦、熱端導流片和熱端焊料層的最大應力分別為245、81.6、270和249 MPa，熱應力的最大值一般出現在邊緣和拐角處。此外，熱電材料主體部分的應力較低，最低可達0.18 MPa。

在模擬過程中也考慮了塑性變形。熱源附近的銅導體和焊料層被視為彈塑性材料，銅導體和焊料層的變形已進入塑性階段，塑性變形可有效緩和STEG中的應力，因此在熱-力學模擬中塑性行為不可忽略。

3.4 單通道模型的熱電和熱力性能

在對圖2所示的STEG進行詳細優化和模擬后，本文搭建了單通道模型并進行數值模擬，以探索帶有STEG的熱管堆的熱電性能和熱力性能。盡管模型中使用了10個STEM，但熱管冷端的溫度分布差別不大，因此只給出1個STEM的結果。

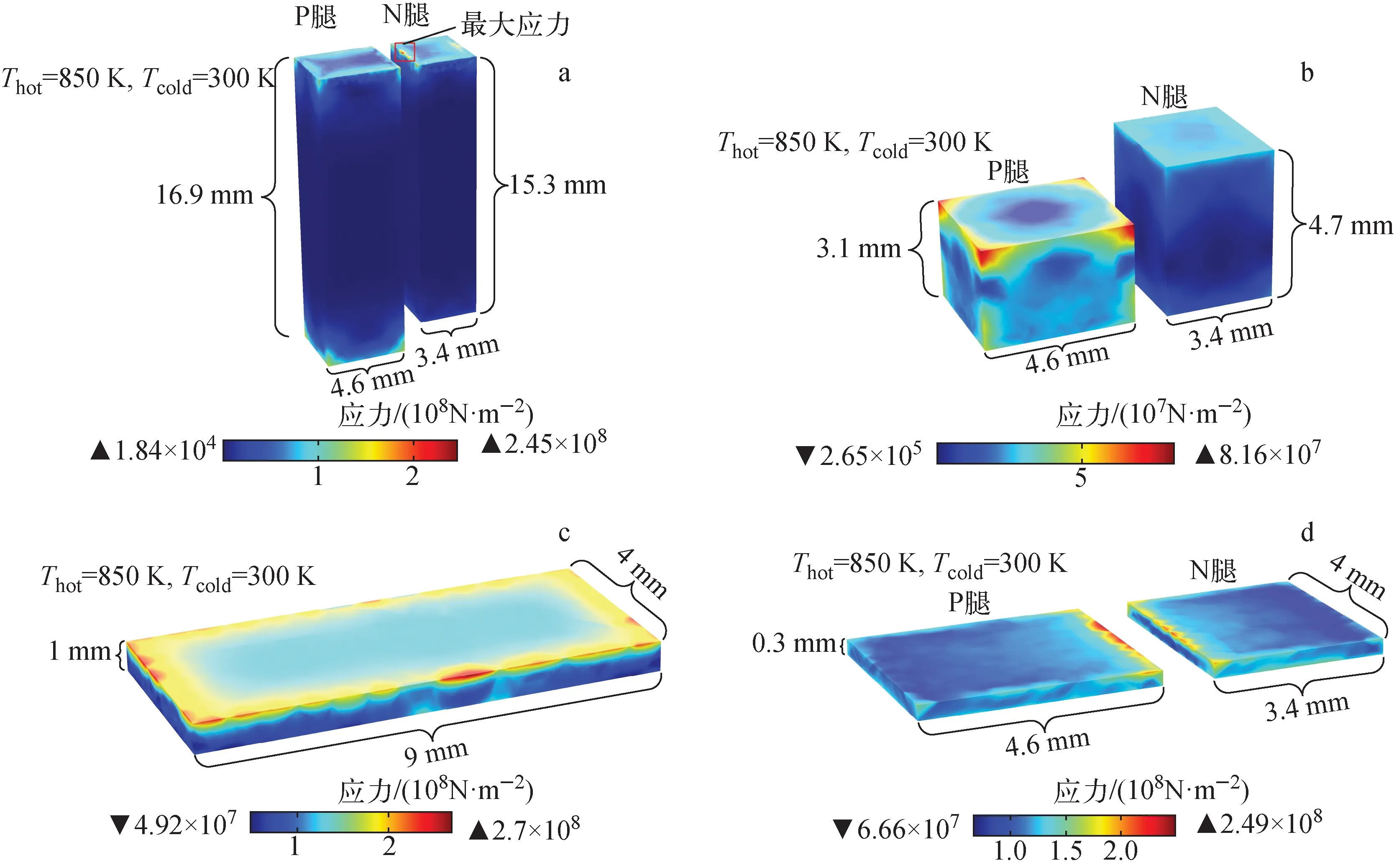
a——碲化鉍；b——方鈷礦；c——熱端導流片；d——熱端焊料層圖11 STEG中各材料的Von Mises應力分布Fig.11 Von Mises stress distribution of different materials in STEG

圖12示出單通道模型，圖13示出STEM的溫度場。如圖12、13所示，從堆芯到STEM熱端的溫降僅為7 K，這說明熱管具有良好的導熱性和等溫性能；溫降主要集中在STEM上，約為537 K。

圖12 單通道模型的溫度場分布Fig.12 Temperature distribution of single channel model

圖14示出單通道模型的熱源改變時熱電轉換效率和輸出功率的變化。由圖14可見，隨著加熱功率的增加，熱電轉換效率和輸出功率也隨之提高，最大熱電轉換效率為15.63%，最大輸出功率為47.29 W。當加熱功率從300 W變為100 W時，熱電轉換效率下降幅度越來越大，每10 W最大下降0.668%。這一現象表明，除停堆工況外，熱管堆應保持在一定的功率以上，以防止熱電轉換效率過度降低。

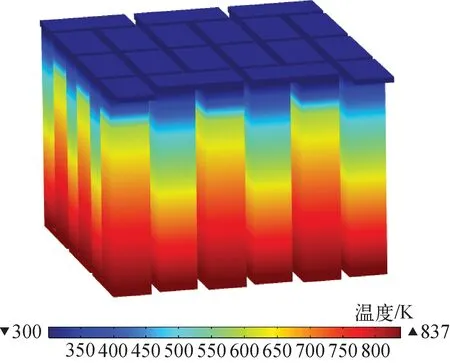
圖13 STEM的溫度場分布Fig.13 Temperature distribution of STEM

與3.2節的模擬和優化結果相比，熱電轉換效率從15.75%降至15.63%，降低了0.565%，這一結果的主要原因是STEG的集成帶來的附加熱阻以及從堆芯到STEM的熱損失。

圖15示出單通道模型中STEM的熱力特性。如圖15所示，STEM的最大應力為547 MPa，主要發生在冷端的絕緣陶瓷板上；最小應力為0.255 MPa，發生在方鈷礦的中部；STEM的最大變形可達0.13 mm。STEM各組件的詳細應力和應變結果列于表2。

圖14 加熱功率變化對熱電轉換效率和輸出功率的影響Fig.14 Effect of variation of heating power on efficiency and output power

圖15 STEM的應力和總位移Fig.15 Stress and total displacement of STEM

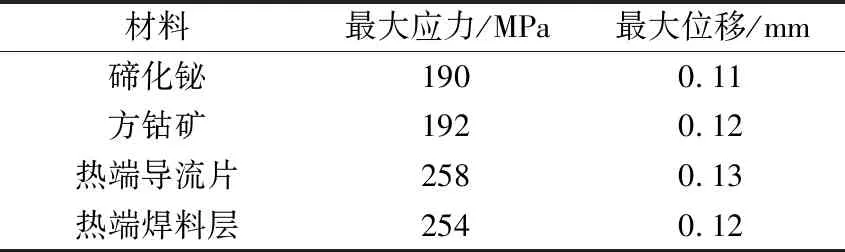
表2 主要材料的最大應力和位移Table 2 Maximum stress and displacement of main material

4 結論

本文提出了一個帶有STEG的熱管堆的概念設計，并建立了熱管堆中STEG的三維有限元分析模型，通過COMSOL軟件對單STEG和單通道模型中的熱電和熱力性能進行研究，研究結果如下。

1) 在設計STEG時，采用銻化鉍作為冷端熱電材料，方鈷礦作為熱端熱電材料，經過數值模擬確定了最佳幾何尺寸。P型支腿的碲化鉍高度為3.1 mm，相應的方鈷礦高度為16.9 mm；N型支腿的碲化鉍高度為4.7 mm，相應的方鈷礦高度為15.3 mm；P型支腿的截面積為4.6 mm×4 mm，對應的N型支腿的截面積為3.4 mm×4 mm。

2) 根據STEG的優化結果，最大熱應力出現在靠近熱端的銅導流片上，約為270 MPa，最小應力出現在方鈷礦上，約為81.6 MPa。

3) 將優化后的STEG進行集成形成單通道模型，并進行性能模擬，結果表明模型的熱電性能從15.75%下降到15.63%，最大應力從270 MPa上升到547.5 MPa。