基于麥克納姆輪的打磨機器人移動平臺仿真分析

槐創鋒，金志裕

（華東交通大學機電與車輛工程學院，江西 南昌 330013）

在人工智能、智能制造的時代，自主移動機器人帶來了一場新的技術創新風暴[1-3]。 根據運動機構不同的類型，自主移動機器人可以被設計為輪式移動機器人、足式移動機器人或者輪足混合式移動機器人，其中輪式移動機器人發展最為廣泛，也是相當流行的研究熱點[4-7]。 AGV（automated guided vehicle）是輪式移動機器人的一個典型代表，在其基礎上的創新應用得到了廣泛的考慮。

隨著科技的進步，移動機器人的自主性、機動性研究吸引了越來越多的關注，其中移動機器人的機動性是移動機器人自主移動的基礎[8-14]。輪式移動機器人運動模式可分為差速輪型、單舵輪型、雙舵輪型、全向輪型。 差速輪型移動機器人靈活性較高，可以原地旋轉，但是不能橫向側移，不適合重載[15]；單舵輪型移動機器人靈活性不高， 雙舵輪型相對于單舵輪型靈活性有提高，但兩套舵輪提高了成本[16-18]；全向輪型移動機器人靈活性最高，可以實現任意方向的移動以及原地旋轉， 成本相對雙舵輪型低，重載能力強。 麥克納姆輪是一種特殊結構的全向輪[19-21]，特點是在輪周邊上有許多成一定角度斜向安裝的輥子，這些成角度的輥子能使輪子旋轉時產生一個橫向運動的效果，四輪麥克納姆輪移動平臺依靠各自輪子的旋轉方向和轉速，最終可以合成任何方向上的運動速度和旋轉從而保證移動平臺能自由地運動。 自主打磨機器人移動平臺的選擇很重要，直接影響打磨機器人的機動性，機動性是打磨機器人實現自主移動、擴大工作范圍的基礎[22-25]。 考慮到麥克納姆輪的眾多優點，自主打磨機器人移動平臺采用四輪的麥克納姆輪平臺， 為了給移動平臺的控制打下良好基礎， 對麥克納姆輪平臺進行了運動學分析。 移動平臺的運動學分析主要有正運動學和逆運動學問題兩類。 由已知移動平臺各輪的轉向和轉速，計算移動平臺相對世界坐標系的速度，即為正運動學問題。要使移動平臺運動到期望的位置，就需要計算出各輪的轉向和轉速，即為逆運動學問題。通過計算機仿真技術可以仿真模擬移動平臺的真實效果，經過實際調試可以達到理想效果。

通過對單個麥克納姆輪進行正運動學分析，接著對四輪麥克納姆輪平臺進行逆運動學分析，運用Simulink 對移動平臺進行逆運動學建模，結合Vrep軟件對移動平臺進行正運動學仿真驗證，將仿真的結果以圖形的形式表示出來，可以直觀地顯示移動平臺的運動情況，為打磨機器人自主移動研究提供理論支撐。

1 單個麥克納姆輪正運動學分析

麥輪是麥克納姆輪的簡稱，麥輪正運動學是指通過4 個輪子設定的相應轉速和轉向以獲得移動平臺中心的運動狀態（速度和角速度）。 麥輪根據輥子安裝角度方向不同分為A 麥輪和B 麥輪， 如圖1 表示A麥輪與地面接觸的輥子，圖2 表示B 麥輪與地面接觸的輥子，分別對A 麥輪和B 麥輪進行正運動學分析。

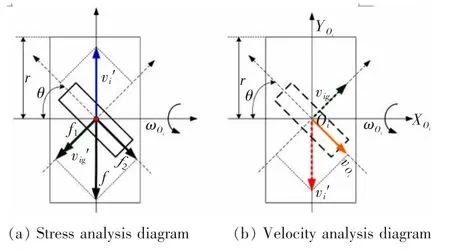
圖1 A 麥輪運動學分析Fig.1 Kinematic analysis of type A Mcnamu wheel

圖1 是A 麥輪的運動學分析圖，圖中輥子安裝角度為θ，A 麥輪繞自身轉軸XOi以ωOi的角速度逆時針轉動（右手定則，大拇指指向，四指彎曲指向的方向），圖1（a）中紅點為與地面接觸的輥子上的接觸點，藍色的速度v′i表示在A 麥輪繞自身轉軸XOi轉動時接觸點對應的線速度， 方向平行于紙面向上。 假設理想接觸麥輪以地面接觸不發生滑動，A麥輪受到地面施加的總摩擦力f，將f 分解為平行于輥子軸線方向的f‖,和垂直于輥子軸線的f⊥，由于輥子屬于從動輪，在f⊥的作用下，會使輥子改變運動狀態并使其順著f⊥的方向轉動起來，從而在接觸點會有相對的線速度vg′。 根據滾輪在地面上滾動時，軸心的速度等于邊緣接觸點的線速度，方向與邊緣接觸點的線速度方向相反。 圖1（b）中v″i表示A 麥輪在地面上滾動時軸心Oi相對的速度，vig表示輥子在地面上滾動時軸心Oi相對的速度，正交分解可以看出速度vig抵消了一部分的速度v″i， 也可以理解為速度v″i和速度vig合成的軸心Oi的總速度vOi，即A 麥輪的實際真實速度，大小為

方向沿著輥子軸線方向（平行紙面右斜向下）。同理對B 麥輪進行運動學分析，如圖2 所示。

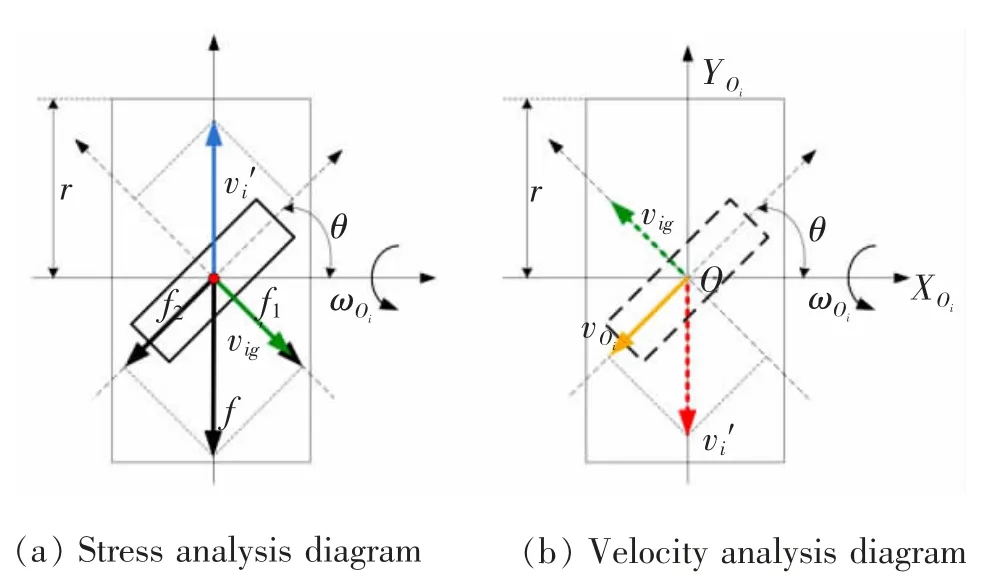
圖2 B 麥輪運動學分析Fig.2 Kinematic analysis of type B Mcnamu wheel

A 麥輪和B 麥輪分別以順時針和逆時針轉動，麥輪軸心Oi的速度vOi有所不同，如圖3 所示。 垂直紙面方向從上往下看，虛線矩形表示下方與地面接觸的輥子，實線矩形表示上方可看見的輥子。

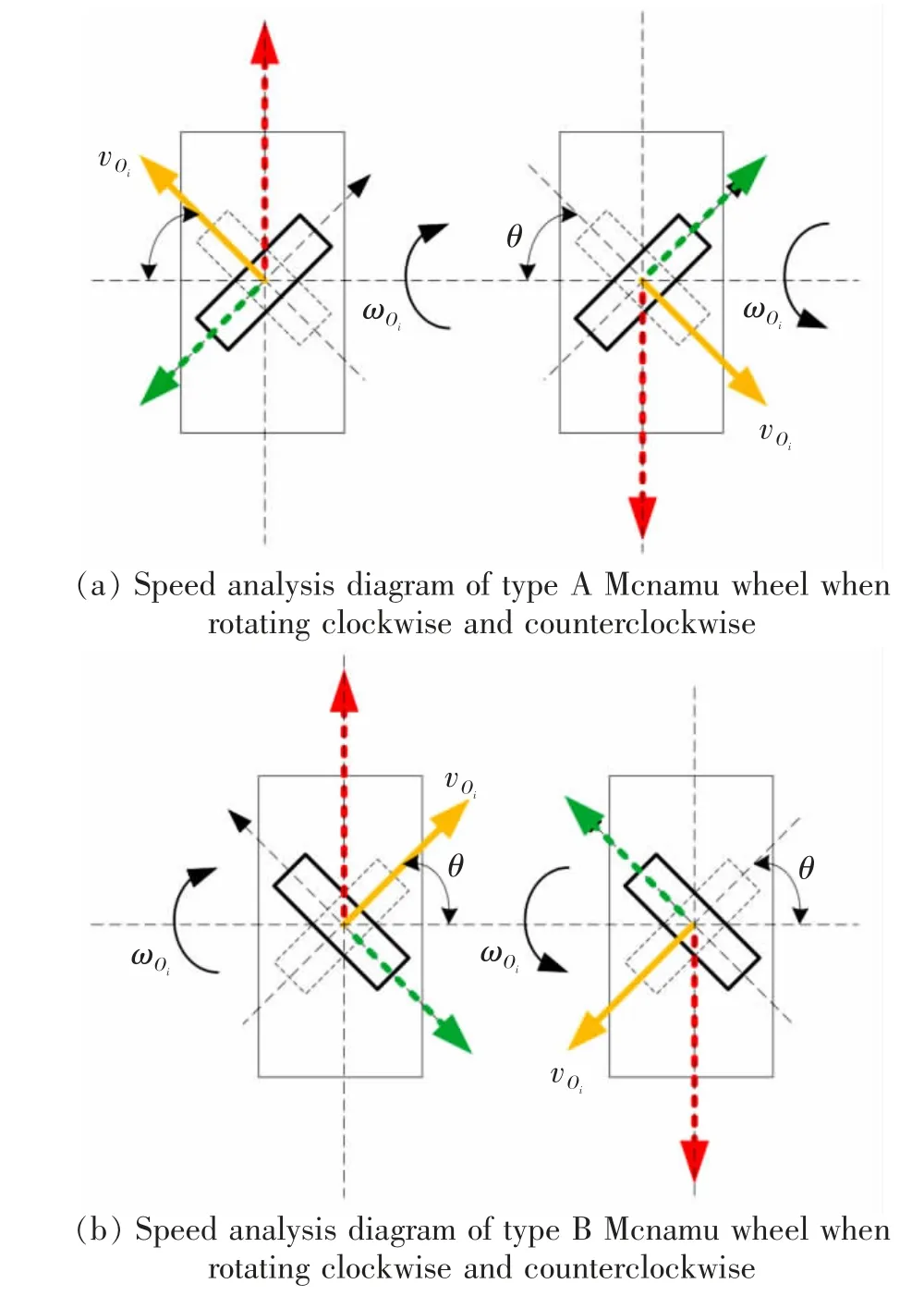
圖3 A 麥輪和B 麥輪速度分析Fig.3 Speed analysis of Mcnamu wheel A and Mcnamu wheel B

圖3（a）顯示A 麥輪順時針和逆時針轉動時速度分析圖，圖3（b）顯示B 麥輪順時針和逆時針轉動時速度分析圖，可以看到A，B 麥輪軸心Oi的速度vOi都是斜向的速度。 A 麥輪順時針轉動時可分解出一個向前的運動和一個向左的運動，逆時針轉動時可分解出一個向后的運動和一個向右的運動；B 麥輪順時針轉動時可分解出一個向前的運動和一個向右的運動，逆時針轉動時可分解出一個向后的運動和一個向左的運動。 正是因為麥輪的這種特性，與傳統輪子相比麥輪可以解決側向運動的問題， 經過組合不同的麥輪以實現全向運動、原地旋轉。

2 四麥輪逆運動學分析

麥輪逆運動學是指已知移動平臺中心速度和角速度，求解4 個麥輪對應的轉速。 上一節已經對單個麥輪進行了正運動學分析，了解了麥輪轉動時軸心速度的大小和方向。 接下來將對麥輪移動平臺做逆運動學分析。

四輪麥輪組合有很多種，但不是所有組合都滿足實際需求。 自主打磨機器人采取B-A-B-A 麥輪組合的移動平臺，如圖4 所示，圖4（a）是移動平臺向前運動時，4 個麥輪對應的轉速和轉向。 對麥輪進行編號，以左前B 麥輪為1，逆時針計數，對應左后A 麥輪為2，右后B 麥輪為3，右前A 麥輪為4。圖4（b）中O 表示移動平臺的中心點，對應坐標系XO－O－YO，Oi表示對應麥輪的中心點，對應坐標系如圖中所示。

圖4 移動平臺運動分析Fig.4 Motion analysis of mobile platform

vO表 示 移 動 平 臺 中 心 的 速 度，vO（i）表 示 移 動 平臺中心速度在i 麥輪坐標系中的速度，ωO表示移動平臺繞中心軸ZO旋轉的角速度。Ri表示i 麥輪軸心到移動平臺的中心點的距離，α 表示移動平臺中心速度與YO軸的夾角，得到移動平臺中心的速度vO（i）與麥輪軸心的速度vOi之間的關系式

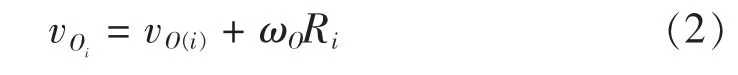
其中

由以上式得式（6）

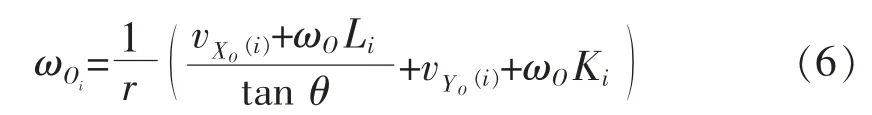
根據式（6），按圖4（b）紅色坐標系建立移動平臺坐標系和各麥輪坐標系，且θ=45°，得到各麥輪轉速與移動平臺運動狀態的關系，如以下式

設世界坐標系為XS-S-YS，如圖4（c）所示,為了降低分析難度， 世界坐標原點與麥輪平臺中心重合， 麥輪平臺中心速度在世界坐標系XS軸上的投影為vXS， 麥輪平臺中心速度在世界坐標系YS軸上的投影為vYS， 麥輪坐標系的XO軸與世界坐標系的XS軸的夾角為δ。 則可得到如下式

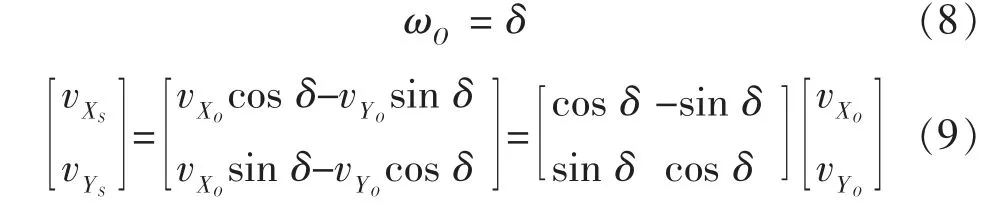
由式（9）得

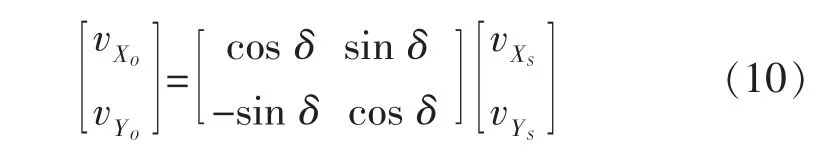
由式（8）～式（10）得式（11）

由式（11）可知

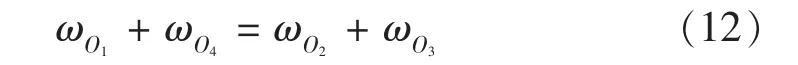
為了便于控制，麥輪平臺平移運動和旋轉運動分開作用，不同時進行，即有速度時，ωO=0；有角速度時，vXS=vYS=0。

3 建立移動平臺仿真模型

3.1 Vrep 軟件介紹

Vrep 軟件全稱為Virtual robot experimentation platform，中文名叫虛擬機器人實驗平臺，現在已經更名為CoppeliaSim。 根據軟件名稱可以知道Vrep是一個針對機器人的仿真模擬器，它集成了許多的開發環境并且是跨平臺的， 提供了多種控制接口，包含了各類現有的機器人模型 （移動式和非移動式）、室內墻壁模型、家具模型、人物模型等，如果Vrep 中沒有合適的模型，也可以快速方便地搭建自己的模型，模型屬性的腳本可以運用多種編程語言進行編程。 Vrep 軟件具有強大的兼容性，在Windows 系統、Linux 系統、Mac 系統都可以運行，擁有多個物理引擎，多方面滿足仿真的需求。 Vrep 相比較于其他仿真軟件，界面更友好，大大提高了仿真的效率。

3.2 麥輪平臺仿真模型搭建

麥輪平臺是打磨機器人機動性的保證， 仿真麥輪平臺的運動特性是十分重要的。 Vrep 在移動型機器人模型中提供了一款KUKA YouBot 麥輪平臺機器人模型，因為只研究麥輪移動平臺的特性，去除YouBot 機器人機械臂部分。 在YouBot 外觀基礎上，搭建自己的麥輪平臺。 麥輪的搭建由兩個旋轉關節組成， 一個關節是提供麥輪旋轉，設置為主動輪；另一關節是輥子旋轉關節，設置為從動輪。 輥子旋轉關節軸相對于麥輪旋轉關節軸成45°。

4 個麥輪模型建立好后，需要為模型添加腳本，實現模型的驅動和運行。 根據式（7）編寫麥輪移動盤平臺的腳本，完成腳本代碼編寫。

4 麥輪運動特性仿真結果

在麥輪正、 逆運動學仿真中分別添加了一個GUI 控制界面，如圖5 所示，方便改變各麥輪的運動狀態，觀看仿真結果。 圖5（a）是麥輪正運動學GUI 控制界面，圖5（b）是麥輪逆運動學GUI 控制界面。

圖5 麥輪正、逆運動學GUI 控制界面Fig.5 GUI control interface of Mcnamu wheel forward and inverse kinematics

4.1 麥輪逆運動學特性仿真結果

在Simulink 中搭建麥輪平臺逆運動學模型，計算不同速度下對應的各麥輪轉速。假設模型參數L=0.6 m，K=0.6 m，r=0.6 m， 對機器人的運動進行模擬，實驗移動平臺在多種情況下運動，包括沿軸正、負方向移動，Y 軸正、 負方向移動，±45°斜移，±135°斜移， 原地逆時針和順時針旋共10 種常見運動案例。

根據麥輪平臺逆運動學Simulink 模型計算每種情況下各麥輪角速度，表1 顯示了移動平臺不同運動狀態下各麥輪對應的角速度。

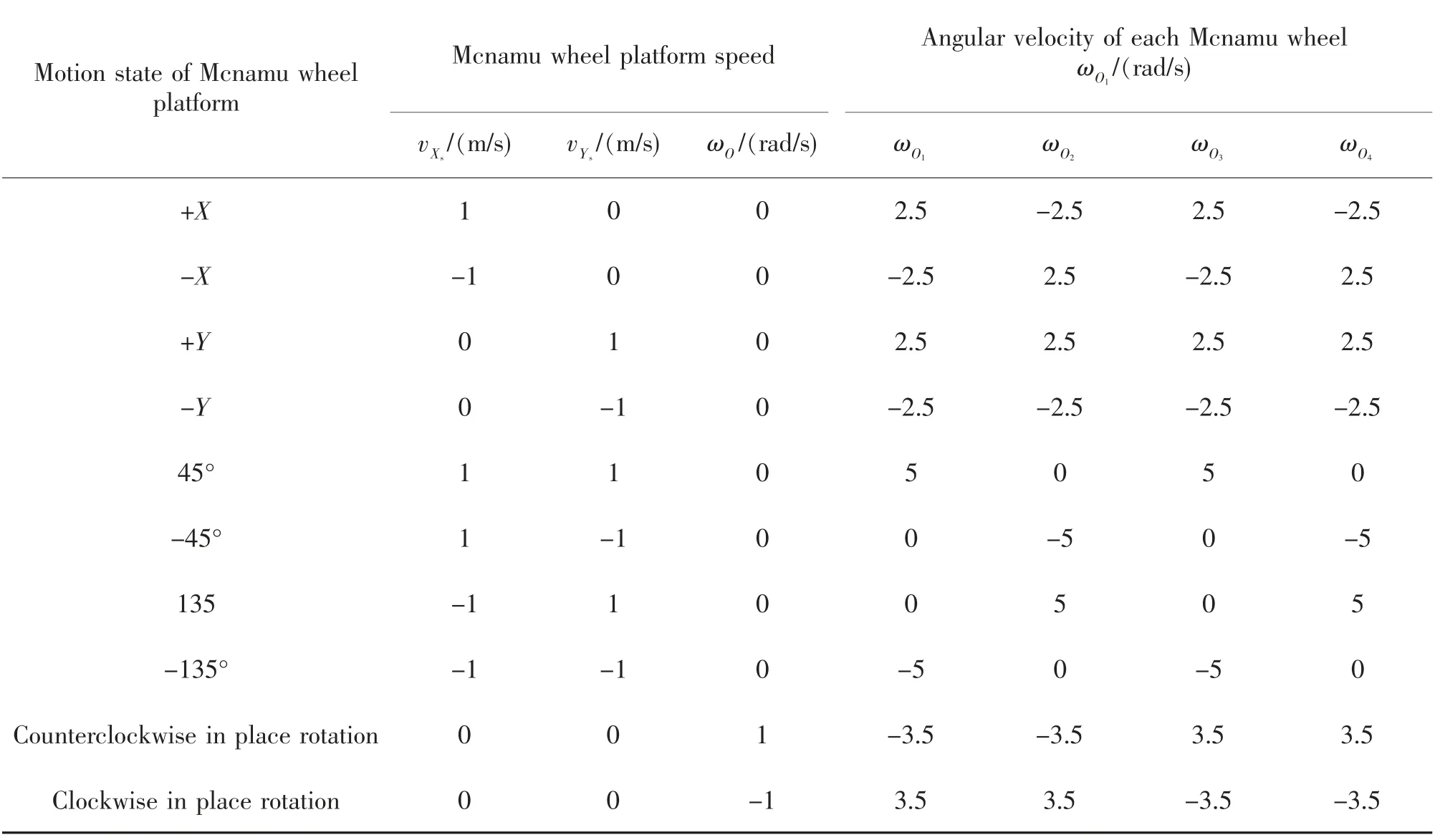
表1 通過求解逆運動學而得到的車輪角速度Tab.1 Wheel angular velocity obtained by solving inverse kinematics

4.2 麥輪正運動學驗證結果

將4.1 中計算的各麥輪轉速輸入Vrep 中搭建的仿真模型中，GUI 控制界面中的值都取整數，若取小數需要除以對應數量級。 由于以上轉速有一位小數， 所以在仿真模型腳本中添加對應取值除以10，得到仿真結果如圖6 所示，從圖6 中可以看到麥輪平臺在各麥輪對應轉速下實現了預期的運動，且可以實現傳統車輪做不到的橫向移動、斜向移動和原地旋轉。

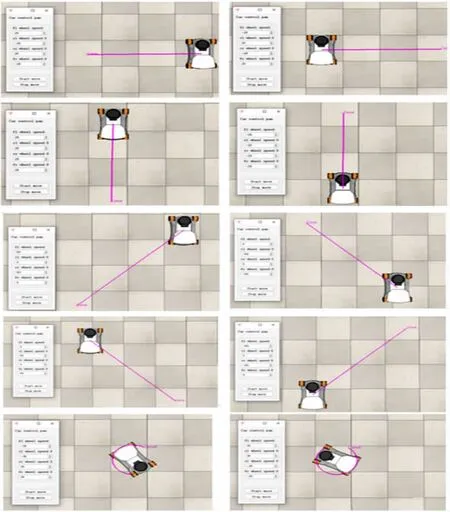
圖6 仿真驗證結果Fig.6 Simulation verification results

4.3 麥輪平臺軌跡運動驗證結果

為了檢驗麥輪移動平臺的全向運動性， 基于ROS 系統對麥輪移動平臺做軌跡運動的仿真驗證，并截取了一百秒數據，如圖7，從圖中可以看到麥輪移動平臺在沿著給定軌跡運動時，移動平臺中心繞Z 軸的角速度值在零附近有一個極小的波動， 由于數量級在千分之一，所以可以忽略不計，說明移動平臺的方位角基本保持不變，證明了麥輪移動平臺可以實現移動平面內全向任意移動。

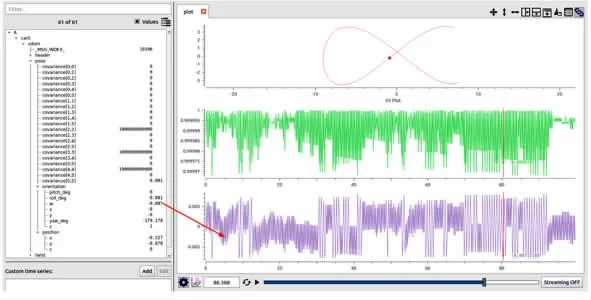
圖7 軌跡運動仿真結果Fig.7 Trajectory motion simulation results

5 結論

1） 通過對麥輪平臺進行正、 逆運動學分析，了解了麥輪的結構、麥輪的運動方式、麥輪安裝組合等，推導出了移動平臺運動學的正、逆解公式。

2） 利用Simulink 建立逆運動學模型計算出各輪的轉向和轉速， 在Vrep 中進行仿真驗證和軌跡運動仿真驗證，結果驗證了麥輪平臺的逆運動學公式的正確性和麥輪移動平臺優秀的全向移動性能。

3） 為控制移動平臺提供理論基礎，為打磨機器人后期的路徑規劃打下良好基礎。