船舶全局路徑規劃相關算法研究綜述

李元昊，段鵬飛，郭紹義，韓 洋，秦 圻

（山東交通學院航運學院，山東威海 264200）

0 引言

船舶的全局路徑規劃就是根據設定的評價標準，為一定航行環境中的船舶搜索出一條由起點至終點的無碰撞路徑，將靜態環境信息的全局規劃和不確定環境因素的動態局部規劃相結合可使船舶路徑規劃達到較為理想的狀態。全局路徑規劃主要應用于相對穩定的環境，其普遍性相對較強。如圖1所示，船舶全局路徑規劃算法可分為傳統全局路徑規劃算法和智能優化全局路徑規劃算法。本文對各類算法的發展背景、設計原理及具體路徑規劃場景下的應用優化進行對比分析，并對全局路徑規劃算法的發展趨勢進行展望。

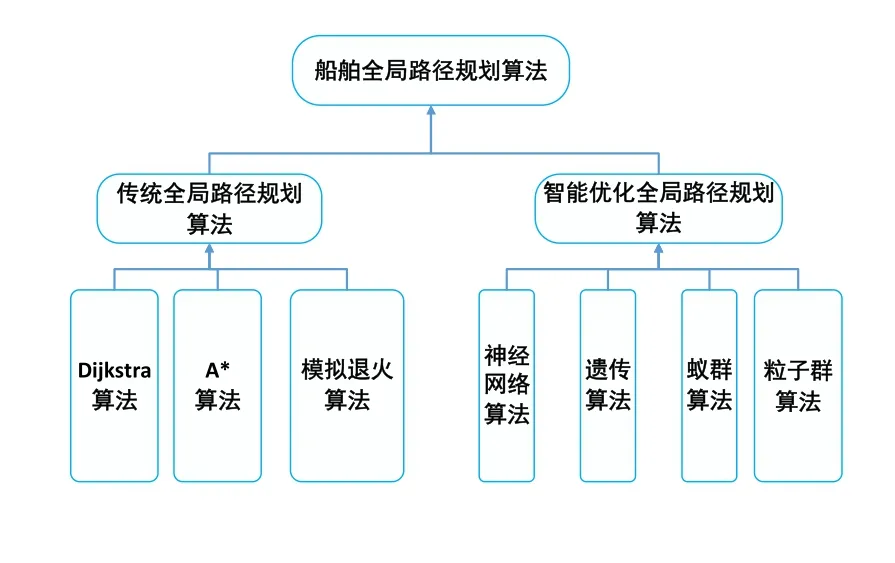
圖1 全局路徑規劃算法分類

1 傳統全局路徑規劃算法

1.1 Dijkstra算法

Dijkstra算法為 Dijkstra在研究貪心算法的過程中提出的解決最短路徑問題的方法，該算法屬于單源路徑算法，可計算質點在運動過程中由起始點運動到其他頂點時的最短距離。宋勇和王文豐等將Dijkstra算法作為路徑規劃初始模型，并在此基礎上進一步改進和優化。杜貽群等針對無人艇進行直角和斜向轉彎的航行特點對Dijkstra算法的路徑搜索進行改進，提出了一種改進的多方向路徑搜索算法，其轉向更為平滑，可充分適應無人艇實際的航行要求，具有很好的適應性。王月鵬利用Dijkstra算法對自主規劃路徑進行優化，實現無人船在水質采樣過程中的多點采樣功能。

Dijkstra算法計算思路清晰，可有效尋找最優解。然而，當路徑規劃較為復雜時，計算所需的數據節點劇增，這會導致運行時間大量增加，進而降低運行效率。

1.2 A＊算法

A算法由Peterhart等提出，該算法將最佳優先搜索算法（Best-First-Search，BFS）和 Dijkstra算法結合在一起。對于靜態環境下全局路徑規劃的最短路徑問題，A算法是最有效的直接搜索算法之一。

A算法的原理：通過設置代價評估函數對節點的綜合優先級進行估計，運用廣度優先思想從起始點為中心向外層層擴展，直至遍歷到終點時得到最短路徑。

熊壬浩等對 A算法的運算過程及改進方法進行了詳細的描述。武善平等和陳新等主要對A算法的啟發函數提出改進，前者利用自適應的改進啟發函數，并著重考慮目標點的方位信息和障礙物的安全距離；后者對啟發函數、分區距離信息和角度變量進行加權處理以提高搜索效率。

由于規劃路徑的轉折點較多、搜索范圍相對較小，A算法容易形成局部最優的情況。張丹紅等和高峰等分別對 A算法的搜索方式和節點搜索領域進行改進和擴展，將八角度、八鄰域節點搜索擴充到多角度、多鄰域的搜索，從而提高空間搜索能力和收斂速度。

相比傳統的Dijkstra算法，A算法在計算目標點與下一個頂點之間的距離的同時會預估目標點與終點之間的距離，進而減少無用的計算量。目前，Dijkstra算法和A算法常與其他算法結合使用，或根據具體的應用場景適當優化以減少計算量。

1.3 模擬退火算法（Simulated Annealing 1.3 Algorithm，SA）

METROPOLIS等最早提出模擬退火算法，KIRKPATRICK等將模擬退火算法應用到組合優化領域。在船舶的路徑規劃中，模擬退火算法更適合用于局部搜索，但其目前在全局路徑搜索的過程中仍起到不可或缺的作用。模擬退火算法通常與其他路徑規劃算法結合使用，以避免出現路徑規劃局部最優的情況。

針對模擬退火算法在水面無人艇在路徑規劃中全局搜索能力不足的問題，鄭佳春等將模擬退火算法與粒子群算法相結合，提出Simulated Annealing Particle Swarm Optimization（SAPSO）混合算法，該算法收斂性好，且能規避局部最優解。SAPSO混合算法適用于不確定因素影響下的動態環境規劃問題。

2 智能優化全局路徑規劃算法

智能優化算法是一種啟發式優化算法，包括遺傳算法、蟻群算法、禁忌搜索算法、模擬退火算法、粒子群算法等。智能優化算法一般是針對具體問題設計相關的算法，理論要求弱，技術性強。智能算法與最優化算法進行比較，相比之下，智能算法速度快，應用性強。對于未知海況環境下控制參數的約束優化問題，可采用智能算法予以有效解決。

2.1 神經網絡算法

神經網絡算法采用并列連接的方式，在路徑規劃時盡量遠離障礙物以使獲得的路徑最短。根據神經網絡算法中各神經元是否存在反饋、是否能接受外加輸入與其他各節點的反饋以及自身的反饋情況，可將神經網絡算法分為前饋神經網絡算法和反饋神經網絡算法。

神經網絡算法通過參數設置實現自我學習的功能，規劃速度快、結構簡單、魯棒性強。神經網絡算法存在以下不足之處：1）泛化能力和記憶能力較差；2）學習速率通常不變；3）學習參數不具備存儲功能。針對神經網絡算法的不足之處，很多學者對其進行相應的優化和改進，或將其與其他算法組合使用。

耿曉龍等和呂揚民等通過將人工神經網絡與強化學習算法中的Q學習算法相結合，以有效解決路徑規劃在不同領域的相關問題。其中，耿曉龍通過在強化學習中設立獎罰規則，將神經網絡與Q學習算法有效結合，得到路徑規劃最優解，并通過實驗仿真對算法進行驗證。

2.2 遺傳算法

遺傳算法是JOHN在生物進化論的自然選擇和遺傳變異觀點的基礎上提出的。該算法通過加入選擇、交叉和變異算子對初始長度編碼下的種群進行運算，并將適應度作為路徑解的評價標準。遺傳算法的邏輯流程見表2。

圖2 遺傳算法的邏輯流程

遺傳算法具有選擇、交叉、變異的特征，故其搜索過程具有靈活多變的特點，可有效提高全局路徑的搜索能力。然而，遺傳算法的計算速度較慢、路徑拐點較多、算法的實時性和適應性較差。

欒志玲與馬建敏等對交叉變異的概率進行自適應調整以提高算法的全局搜索效率，使用自適應交叉變異概率替代現有交叉變異概率以避免早熟現象的出現。欒志玲提出一種改進遺傳算法，在原來基礎之上增加種群熵對種群多樣性進行評估，并通過Matlab仿真驗證了算法的可行性。

馬丹提出使用精英保留策略方法來解決遺傳算法收斂性慢的問題，提出增加免疫算子來解決遺傳算法多樣性減少的問題。文獻[23]提出一種改進策略，通過增加插入、刪除算子對路徑編碼進行優化，可有效提高解空間內的尋優效率。

2.3 蟻群算法

蟻群算法屬于生物啟發式類的算法，其最鮮明的特點在于螞蟻群體的多樣性和路徑搜索的正反饋特性。在選擇路徑的過程中，路徑選擇概率和信息素揮發系數是決定全局尋優能力的重要因素，由初始信息素和啟發信息的大小決定。

路徑選擇概率和啟發信息的計算公式分別為

式（1）和式（2）中：下標和為節點；為節點數量；為時刻；和分別為信息素因子和啟發函數因子，反映信息素和啟發函數對螞蟻下一步轉移作用的強度；為兩節點間的直線距離。

由式（1）可知，信息素和啟發信息與路徑選擇的概率之間存在正相關關系。該算法的正反饋特性可使算法在搜索過程中不斷收斂，最終逼近最優解。

啟發式的概率搜索具有著跳出局部最優解的特點，多個體同時搜索的效率相比單個體搜索得到明顯提高。然而，算法中個體分布情況會導致算法的收斂速度與種群多樣性之間存在矛盾。隨機選擇探索全局空間最優解大概率可找到最短路徑，但需要很長時間才能發揮正反饋的作用。

針對傳統蟻群算法初期搜索效率低、收斂較慢的問題，王成等采用不均勻分布初始信息素、引入權重因子等方式對蟻群信息更新規則進行改進。賀嘉等將雙向搜索算法融入傳統蟻群算法，可顯著提高搜索效率，模擬仿真及實船試驗驗證了算法的可行性。

童幫裕等針對冰區航行路徑規劃的特殊性，考慮航線距離、航行操作復雜度和流冰規避等影響因素，結合人工勢場法對蟻群算法進行改進，利用新的啟發信息函數進行路徑選擇。研究結果表明：該算法在在動態避讓、航速控制方面仍有待改進和優化。

馬小銘等提出一種改進蟻群算法，主要通過引入環境因子以調整啟發函數，進而降低死鎖情況的發生，該算法對于船舶路徑規劃問題具有重要借鑒意義。王成等通過引入懲戒因子對陷入死鎖的信息素進行懲罰，進而降低死鎖率。然而，該方法沒有考慮發生死鎖的環境細節。EBERHARTR等通過引入環境因子以增強對環境的閱讀能力，進而有效避免死鎖，提高有效螞蟻的數量。

2.4 粒子群算法

粒子群算法由EBERHART等提出，屬于概率型全局路徑規劃算法。該算法不斷對個體和群體的最優位置進行搜索，直到找到全局最優解。其中，個體優劣程度的適應值評價函數直接影響到算法的執行效率，下面通過流程圖的方式對算法原理進行說明。粒子群算法的邏輯流程見圖3。

圖3 遺傳算法的邏輯流程

粒子群算法從隨機解出發通過迭代尋找最優解，且可調參數較少，故其具有應用簡單、收斂速度快、計算復雜程度較低等特點，但同樣存在尋優過程中種群多樣性和算法收斂速度上的矛盾。

王文豐等利用線性遞減慣性權重粒子群算法進行路徑規劃，引入混沌理論對種群進行初始化，以平衡種群的全局搜索能力和局部搜索能力。宋勇對線性遞減慣性權重粒子群算法以及引入混沌理論的改進算法進行了更加詳細的描述，并在此基礎上進行動態避障研究。通過結合局部動態的路徑規劃中改進的滾動窗口算法對動態威脅區域進行有效的規避，進而得到最優路徑解。

針對多路徑規劃問題，劉利強等在粒子群算法的基礎上引入小生境識別、粒子群隔離算法、交叉算子等，將種群粒子分為主群粒子和子群粒子，在此基礎上完成區域內局部尋優，從而有效規劃出多條最優及次優路徑。

鄭佳春等將粒子群算法與模擬退火算法相結合，對無人船艇的路徑規劃進行研究。舒宗玉采用混合粒子群算法對初始路徑進行優化，并在路徑最短基礎上提出路徑平滑和路徑安全的多目標優化問題，但仍需進一步精確測量才能符合實際要求。

3 發展趨勢分析

1）結合具體應用環境與算法特點優化常規算法性能

為獲得路徑規劃的最優解并使得所規劃的路徑符合各種航行環境和應用場景，對各種規劃算法的運用大致可分為以下3種：（1）對常規算法中的不足進行改進；（2）利用多種算法的優勢進行適當的算法綜合；（3）將改進優化算法與常規的某類算法進行結合產生新的混合算法。在保證路徑規劃有效性的同時，主要通過控制算法的收斂速度、提高全局搜索的效率、防止局部收斂的出現等方式來提高算法性能。

2）仿真與實船試驗對路徑規劃理論計算結果驗證有待進一步的完善

針對路徑規劃算法的研究目前大都還處于理論描述以及模擬仿真驗證階段，僅有少數的研究通過仿真和實船進行驗證。通過實船對算法過程的驗證往往與理論計算有一定的差距，雖然對實驗設計的要求較高，但更能直觀反映方法在真實海洋環境中的應用效果，可以對存在的隱患問題和突發狀況進行排查，并選擇更適合的解決方案以適應海洋航行的需要，降低航行突發風險的發生概率，也能使算法的實用性和推廣性得到保障。

3）借鑒其他領域研究成果使全局路徑規劃與局部路徑規劃相結合

當前對路徑規劃的研究往往在全局路徑規劃的基礎上對局部不確定因素下的動態規劃進行綜合考慮，或對多目標條件或多路徑條件下的路徑規劃問題進行研究。對環境感知的動態路徑規劃算法在機器人路徑規劃中應用廣泛，對無人船在復雜環境下的路徑規劃幫助很大。

4 結論

船舶路徑規劃算法對于無人艦艇在各種環境下的自主航行至關重要，本文對各類算法的發展背景、設計原理及具體路徑規劃場景下的應用優化進行對比分析，并對全局路徑規劃算法的發展趨勢進行展望，希望為無人艇全局路徑規劃算法的優化提供一定指導。