基于擴展卡爾曼濾波的車輛運動軌跡估計方法研究

龍杜輝

（200082 上海市 上海理工大學機械工程學院）

0 引言

目前車輛上使用的定位技術主要有全球定位系統（GPS）、航位定位系統（DR）、慣性導航系統（INS）和同時定位與建圖（SLAM）。GPS 具有全球性、精度高等特點，但是受外界干擾最大；DR 利用車載的傳感器測量車輛的車速、加速度、偏航角速度來實現車輛的自主定位。在短時間內，DR 精度是很高的,但由于累計誤差的存在，經過一段時間后，定位系統就會失效；INS 跟DR 一樣短時間的精度高，但是定位誤差會隨時間累積[1-2]；SLAM 通過雷達或相機對周圍環境進行掃描，來估計自身的位置，但是隨著環境的幾何特征和紋理特征的不明顯，定位也會失效，而且SLAM 使用的傳感器成本比較高[3]。每一種傳感器進行定位都有優點，同時也存在弊端。利用多傳感器的信息融合估算運動軌跡，可以避免單一傳感器定位的弊端。本文利用擴展卡爾曼濾波器對車載編碼器和IMU 采集的信息進行融合，實現車輛的自主定位，對比融合后的軌跡和真實軌跡，證明了該方法的有效性。

1 差速模型的建立

本文實驗對象是兩后輪獨立驅動的小車模型，如圖1 所示，它能通過調節兩輪的速度差達到轉彎目的，這種運動模型叫做雙輪差分驅動模型[4]。

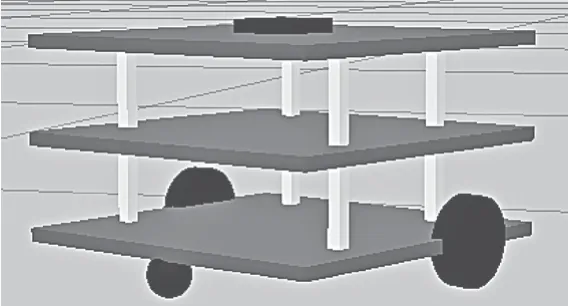
圖1 小車模型Fig.1 Car model

小車的原點位于兩輪軸的中心位置。用該模型估算小車位置只需2 個主要參數：車輪之間的距離d 和車輪半徑R。運動模型如圖2 所示，一般情況下，通過兩車輪上編碼器測量每個時間步長δt 的左右車輪轉過角度δψL、δψR計算小車位姿的變化。假設x 正方向為小車前進的方向，小車左邊為y 正方向，z 的正方向垂直于小車向上。因此各運動狀態下模型如式（1）—式（7）。

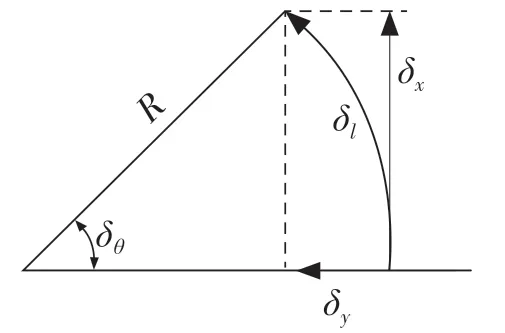
圖2 運動模型Fig.2 Motion model

直行時：

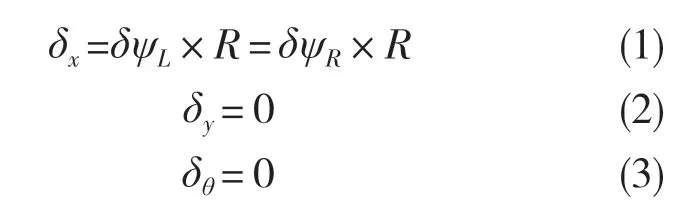
轉彎時：

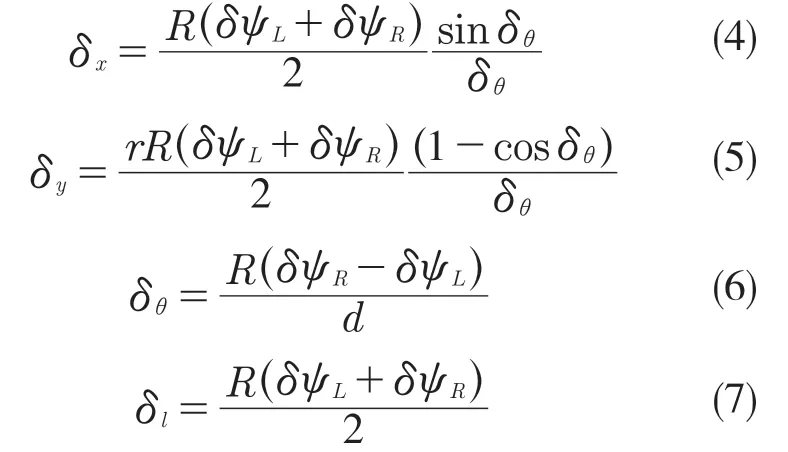
小車運動方式通過局部位姿增量進行改變，累加局部位姿增量即可得到小車的運動軌跡，因此利用小車的編碼器數據獲得了車輛的里程計模型。由于車輛運動累積具有不確定性，需要協方差矩陣Q 來表示這種不確定性關系，它可以通過兩驅動輪轉角測量值的不確定性來如式（8）表示：

式中：J——運動模型的雅可比矩陣；Qη——輪子角度測量值的協方差。

2 IMU 驅動模型的建立

IMU 由加速計和陀螺儀組成[5]，它能測量車輛的線加速度as和角速率ωs。通過IMU 得到的線加速度和角速率可以用來預測小車位姿。式（9）為IMU 計算的狀態量和誤差，式（10）—式（14）為狀態量和誤差更新過程。

式中：p，v，q ——慣性測量單元的參考系的位置、速度和方向四元數；ab，ωb——加速度計和陀螺儀的偏差；vi，θi——在時間間隔Δt 內的測量誤差；ai，ωi——加速度計和陀螺儀偏差的隨機游走。——四元數相乘，R{q}——關于方向角q 的旋轉矩陣，這里僅考慮2D 情況下，則R{q}如式（15）所示：

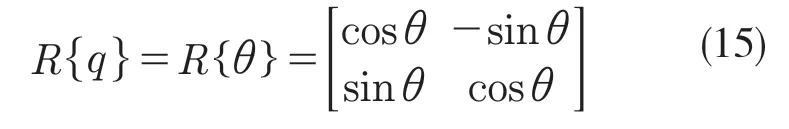
3 基于擴展卡爾曼濾波的車輛位置預測

3.1 擴展卡爾曼濾波器

擴展卡爾曼濾波器[6]是在卡爾曼濾波基礎上進行改進，使其適用于非線性系統。主要應用的方法是在上一時刻的后驗估計狀態量下進行泰勒展開得到這附近的線性系統，然后再對系統狀態進行估計。擴展卡爾曼濾波分為預測和更新2 個部分，如圖3 所示。

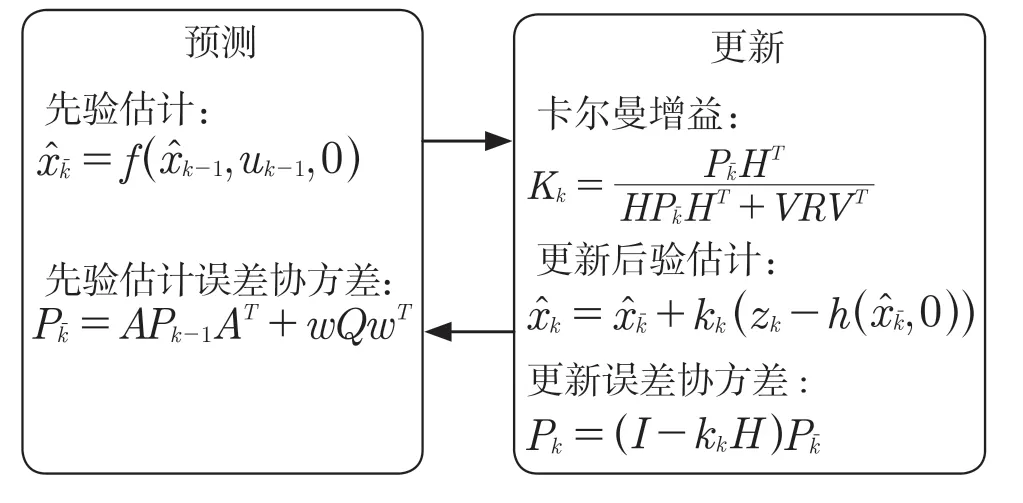
圖3 擴展卡爾曼濾波過程Fig.3 Extended Kalman filtering process

3.2 多傳感信息融合

由于慣性測量單元IMU 估算的車輛的運動軌跡相對于編碼器的估算來說在短時間內準確度更高，但由于IMU 中加速度計和陀螺儀的雙重誤差累積，在長時間的運作下，對車輛的定位準確度明顯下降，此時應更相信由車輪編碼器估算的軌跡。

為此，提出了一種基于信息融合的擴展卡爾曼濾波器策略，來精準定位車輛位置和軌跡預測方法。此系統同時接收來自編碼器信息以及慣性測量單元的數據。通過組合定位系統的數學模型，可以融合兩個系統的數據，獲得車輛位置的精準估計。融合過程的流程圖如圖4 所示。

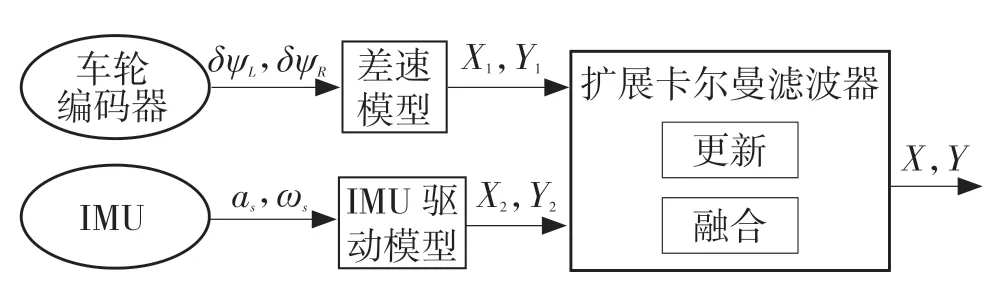
圖4 多傳感數據融合過程Fig.4 Multi-sensor data fusion process

多傳感的數據融合可以將其中一個傳感器的數據作為測量量，另外一個傳感器的數據當作觀測量進行融合[7]。以下為多傳感的融合模型。

（1）以車輪編碼器數據作為預測模型：

式中：xk=[xo，yo，θo]T——車輛在k 時刻平面坐標及轉角的三維向量；f ——k-1 時刻與狀態向量xk-1、系統控制輸入量uk-1有關的非線性函數；Wk-1——系統在k-1 時刻的高斯白噪聲，呈正態分布。

（2）以慣性測量單元數據作為觀測模型：

式中：zk=[xi，yi，θi]T——k 時刻三維的觀測向量；h——k 時刻關于狀態向量xk、系統控制輸入量vk的非線性函數；Vk——系統在k 時刻的觀測噪聲，呈高斯正態分布。

3.3 定位評價標準

評價一種算法設立評價標準是必要的[8]。本文采用定位誤差和定位的成功率作為評價準則，其方法如下：

3.3.1 定位誤差

定位誤差表示估計位置與真實位置偏差，表達式為：

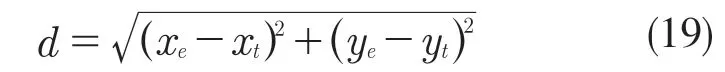
式中：d——使用融合算法后的位置與真實位置的偏差；xe、ye——通過融合算法估計的車輛坐標；xt、yt——此時刻車輛真實坐標。

3.3.2 定位準確率

定義當使用融合算法后與真實位置的偏差d 小于車輛的1/5 時為定位成功，否則設為定位失效。這里使用的小車模型長寬都為38 cm，故取判斷定位成功的閾值為7.6 cm。定位準確率即為定位成功次數與實驗測量總數的比值：

4 實驗驗證

本文基于ROS 操作系統中gazebo 的仿真環境，完成車輛行駛的仿真實驗。傳感器數據由gazebo環境中，小車上傳感器插件模型提供話題數據，將IMU 和差速模型得到的里程計數據在ROS 的工作空間中進行融合，得到融合后的話題數據，將這些話題打包成bag 文件，并導入MATLAB 軟件，結果如下所示。

圖5 中，小車從圖5（a）依次運動到圖5（d）。由圖6 可知，由多傳感融合算法估計出來的軌跡與真實軌跡是十分接近的，在抖動區間也能準確預測真實軌跡。

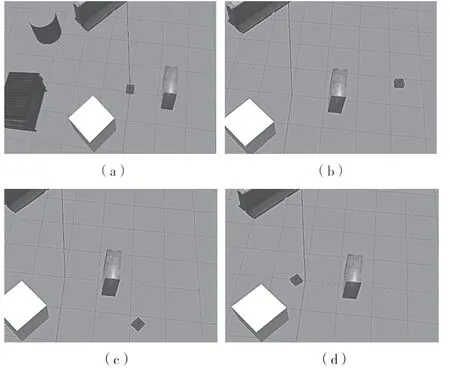
圖5 小車在gazebo 運動過程Fig.5 Movement of trolley in Gazebo

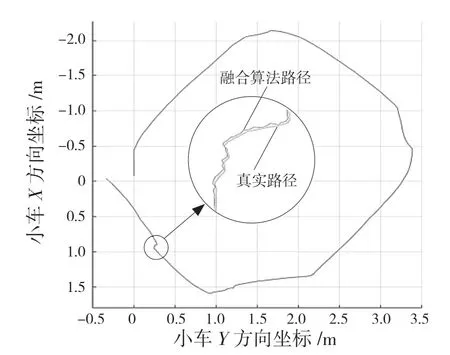
圖6 小車運動軌跡Fig.6 Trajectory of trolley

為了定量判斷擴展卡爾曼濾波器對多傳感融合的定位效果，在所有的數據點中隨機依次抽取10 個測量點作為判斷指標，分別與真實值進行比較，處理后的數據如圖7—圖9 所示。

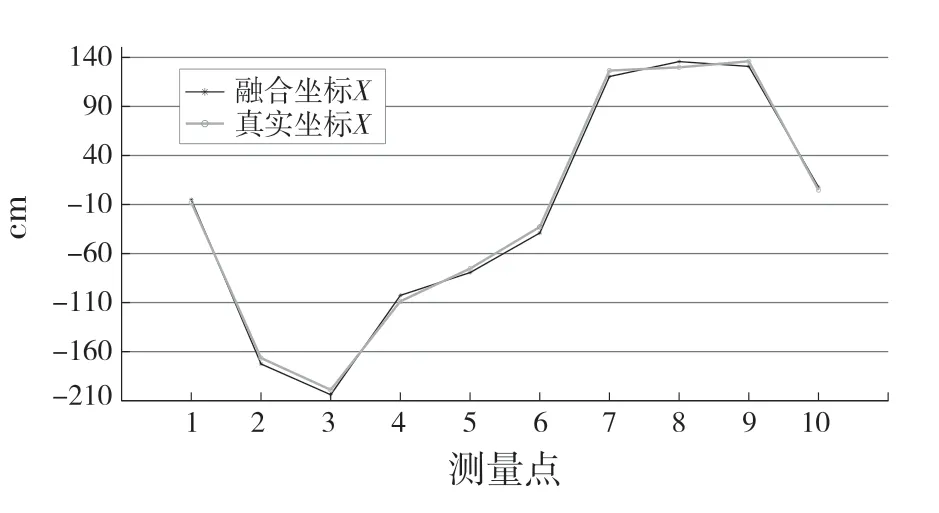
圖7 小車X 軸方向上對比Fig.7 Comparison of trolley in X-axis direction

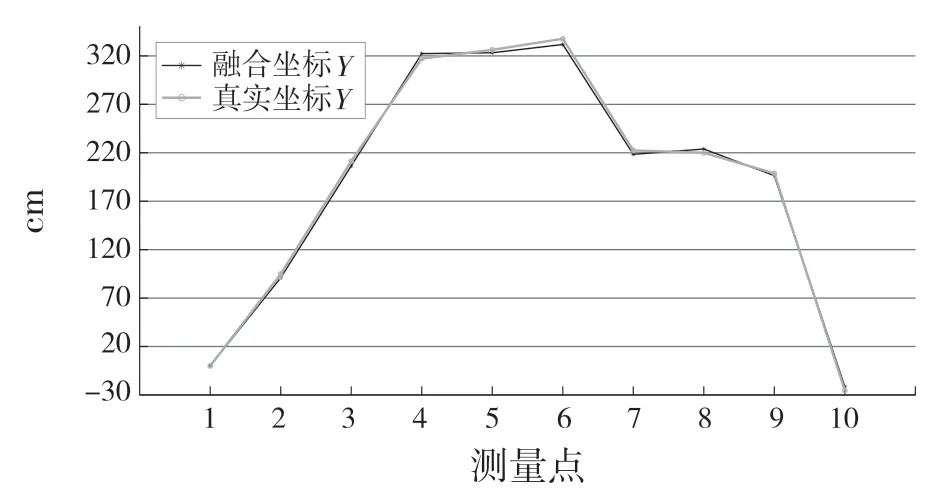
圖8 小車Y 軸方向上對比Fig.8 Comparison of trolley in Y-axis direction

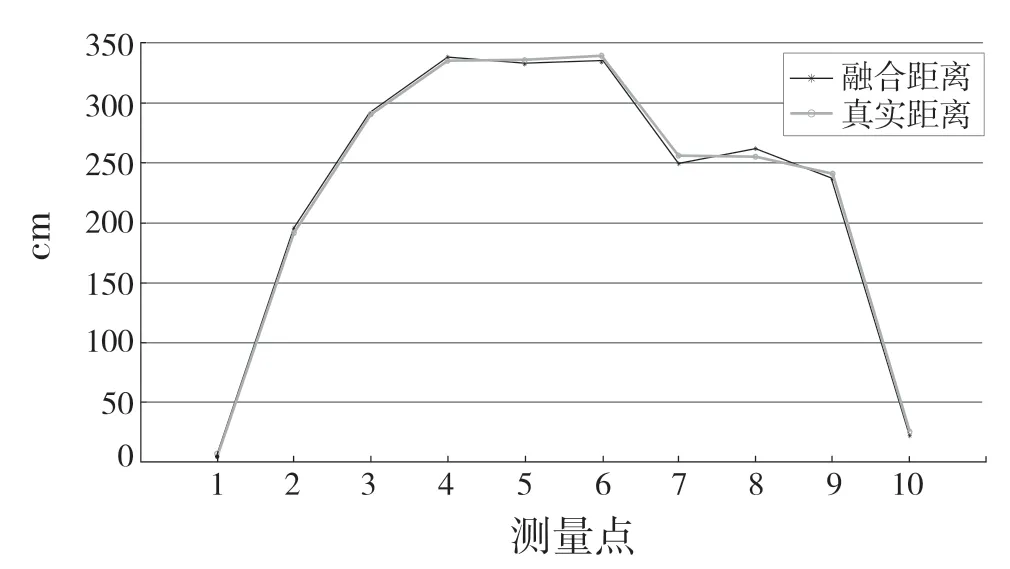
圖9 小車與原點距離對比Fig.9 Comparison of the distance between trolley and origin

根據定位評價標準對該實驗結果進行分析。由圖10 可知，在隨機的10 個測量點中只有測量點4 和測量點6 大于判斷閾值，故定位失敗。由式（20）可得小車在本次實驗的定位成功率μ=80%。

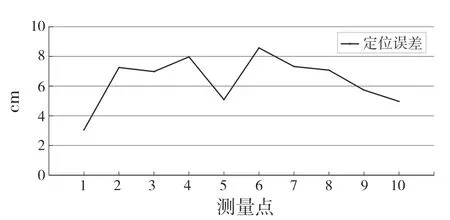
圖10 定位誤差分析Fig.10 Positioning error analysis

由于卡爾曼濾波器只利用了上一時刻的數據和系統的輸入量，計算量是比較小的，所以相比于其它算法而言，實時性和魯棒性都是比較優異的。

5 結論

（1）本文以小車模型為研究對象，針對車輛定位容易失效的問題。通過利用擴展卡爾曼濾波對編碼器和IMU 數據進行融合，提高了定位的準確性，實現了自主定位。

（2）通過對定位誤差的定量分析，驗證了本文算法對提高車輛定位是有效的，并且可以僅通過車載傳感器實現自我定位，解決了在復雜環境下定位失效的困惑。

（3）本次研究也存在許多不足的地方。首先本次實驗是基于仿真的，故誤差設定會比較不合理，設定編碼器和IMU誤差類型均符合高斯正態分布，這與實際誤差存在著差異，且設定的方差比較小；其次仿真的模型小車與真實車輛也存在一定的差異。后續研究可以考慮采用真實的模型進行實驗驗證，然后加入相機、雷達進行多傳感融合，繼續提高定位進度。