GNSS RTK定位對中桿傾斜補償技術及精度分析

鄧力中，郭際明，馬 俊，趙胤植，許 毅

（1.武漢大學測繪學院，湖北 武漢 430079；2.中鐵第四勘察設計院集團有限公司，湖北 武漢 430063）

在RTK測量中，GNSS接收機測量的位置不是直接在目標點，而是在天線相位中心。為了優化GNSS信號的接收，天線通常安裝在天線桿上[1-3]。對于在RTK測量中常用的天線桿，通過手工調整使圓氣泡居中來來調平天線。這種作業方式存在三方面的問題，一是調平對中桿需要時間，影響作業效率；二是調平會受到人為誤差和儀器缺陷（如調整不當的氣泡）的影響；三是在實際測量工作中，由于受到測量地點障礙物的遮擋，使得許多待測點都無法直接進行測量，比如在頂端安置了接收天線的對中桿不能直接垂直放置于墻角，無法直接測量墻角下的待測點，必須向外傾斜，并且由于障礙物使得RTK接收機接收的衛星信號差，天線桿需要向外傾斜一定角度以獲得更好的衛星信號[4-6]。為了解決這些問題，就需要采用傾斜補償技術，解決對中桿傾斜狀態下的頂部天線相位中心到底部測量點的自動歸算問題。在進行RTK測量時對對中桿進行實時傾斜補償，可實現對中桿在傾斜安置狀態下的點位快速測量，不再需要整平或是后期的校正，能夠把對中桿底點斜置于墻面內直接測量得到隱蔽點的坐標，將提高RTK測量的工作效率[7]。

1 GNSS RTK定位對中桿傾斜補償原理與方法

當對中桿向某一方向進行傾斜測量時，如圖1所示，設其傾斜角為θ，方位角為α，其桿長為S，對中桿在水平面的投影長度為D，GNSS接收機天線相位中心位置在水平面投影位置坐標為(x′，y′，H′)，則待測點的實際坐標應為( )

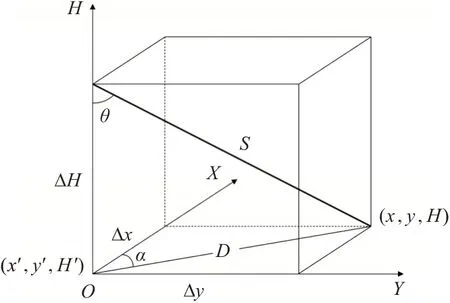
圖1 對中桿傾斜補償的基本原理

x，y，H：

式中，在x、y、H方向上的改正數Δx、Δy、ΔH為：

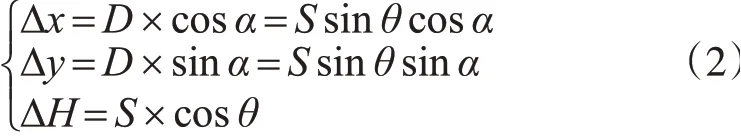
2 對中桿傾斜補償GNSS RTK定位實驗

2.1 實驗設備

實驗選取了徠卡GS18作為實驗設備，其傾斜補償技術方法是實時確定對中桿的姿態，通過儀器內置的慣性傳感系統進行傾斜補償。MEMS IMU包含一個三軸加速度計和一個三軸陀螺儀，向慣導系統提供精確的加速度和角速度信息。GNSS獲取位置和速度信息輸送到INS和內置機載軟件模塊。基于GNSS位置、INS姿態和桿長，機載軟件就可以通過計算，得到傾斜狀態下的對中桿底部端點的位置。

2.2 對中桿傾斜補償精度分析

2.2.1 實驗方案

本次實驗首先在武漢大學信息學部選取了觀測條件良好的點位，通過長時間靜態觀測，精確測定目標點的坐標作為已知參考值。然后利用GS18在目標點以不同傾角和不同方位角進行測量，對比不同情況下得到的坐標值及其變化，以確定其傾斜補償的精度。

2.2.2 實驗分析

對中桿桿長為1.8 m，通過對中桿支架控制對中桿的傾角，選取8組適度間隔的水平方位區間，在每組水平方位區間內，分別在約10°、20°、30°、40°的傾斜角下進行RTK測量。水平方位和傾斜角組合后共形成32個對中桿觀測狀態，每個狀態下觀測10次，實驗得到站心坐標系（NE）下的320次觀測結果的平面坐標誤差分布散點圖如圖2所示，對中桿每個狀態的10次RTK測量的平均值對應的平面坐標和高程誤差具體數值見表1所示。

從圖2可以看出，經過傾斜補償后得到的各組坐標誤差與在組內相對集中，但點位誤差出現的水平方位與實驗時選定的對中桿的傾斜方向的水平方位并不一致，在各組之間相對分散，說明最終定位誤差與水平方位有一定的關聯性，但點位誤差在水平方向上發生了不同程度的偏轉。

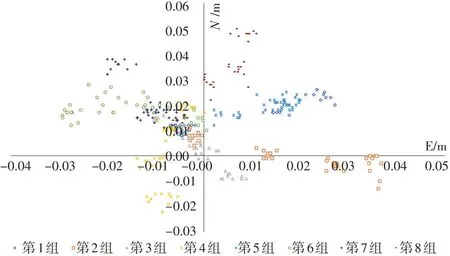
圖2 傾斜補償實驗的點位坐標分布散點圖

由表1可見，整體的傾斜補償導致的坐標誤差存在明顯的隨傾斜角度增大而增大的趨勢，其最大的坐標誤差值出現在第8組傾斜角為44.159 2°、方位角為313.614 8°的對中桿狀態，此時其點位誤差為0.05 m。下面將分別對ΔN、ΔE、ΔH在不同傾斜角及不同方位角的情況下對比分析其誤差情況和傾斜補償精度。

（3）關閉發射器：澆鑄結束將發射器右上角旋鈕鑰匙由"ON"打至"OFF"，按下左上角急停按鈕松，此時指示燈顯示紅色，即可終止1-14鍵的功能操作。

表1 不同方位角及傾斜角下的測量結果

1）傾斜角對傾斜補償精度的影響。首先我們按照方位角大小順序將8個測量方向命名為8個組別，分別為第1、2、…、8組。由實驗結果可得，在ΔE值方面，當對中桿處于第4、5、6、7組狀態時，其誤差值會明顯隨傾斜角度增大而向正方向增大；當對中桿在第7組狀態時，其ΔE數值先是逐漸增大，當傾斜角超過30°后又逐漸減小；而當對中桿向方向1、8進行傾斜時，ΔE值沒有明顯的變化；但在向方向2進行傾斜測量時，其ΔE值先是向正方向增大，傾斜角度達到80°之后，又開始向負方向增大，最大達到-0.021 1 m。

對于ΔN來說，當對中桿處于第4、5組狀態時，其誤差值會明顯的隨傾斜角度增大而向正方向增大；處于第6、7、8組狀態時，其誤差值會明顯的隨傾斜角度增大而向負方向增大；當對中桿處于第1、2組狀態時，ΔN值沒有發生明顯的變化。在第1組狀態下進行傾斜測量時，在傾斜角小于30°時，ΔN的值沒有明顯的變化；當傾斜角大于30°后，其誤差值會明顯的隨傾斜角度增大而向正方向增大。

在ΔH值方面，除去在第1、3組狀態的情況以外，當對中桿處于另外6個組的狀態時，其誤差值均明顯的隨傾斜角度增大而向正方向增大；當對中桿處于第3組狀態時，ΔH值沒有發生明顯的變化；而當對中桿處于第1組狀態時，其ΔH值先是隨傾斜角增大而向正方向增大，當傾斜角超過30°后，又慢慢回落到0.01 m左右。

對整體的點位誤差來說，當對中桿處于第2、4、5、6組狀態時，其誤差值會明顯的隨傾斜角度增大而向正方向增大；當對中桿向方向處于第8組狀態時，其點位誤差值沒有發生明顯的變化；而當對中桿處于第3組狀態下，傾斜角小于30°時，點位誤差值沒有明顯的變化；當傾斜角大于30°后，其誤差值會明顯的隨傾斜角度增大而向正方向增大；當對中桿處于第1、5組狀態時，其點位誤差值的變化趨勢和變化幅度相似，只不過其數值變化的方向相反。

總體而言，傾斜角對于傾斜補償精度有如下的幾點影響：

1）誤差值呈現明顯的隨傾斜角度增大而增大的趨勢。可以看到在大部分的點位都出現了誤差值隨傾斜角度增大而增大的情況。由圖4可知，當傾斜角度小于30°時，各點位在E、N、H方向上的誤差值基本小于2 mm，其綜合點位誤差也基本小于3 mm；但當傾斜角度大于30°以后，在各個狀態下其誤差值都有較大幅度的增加，其點位誤差最大達到5 mm。

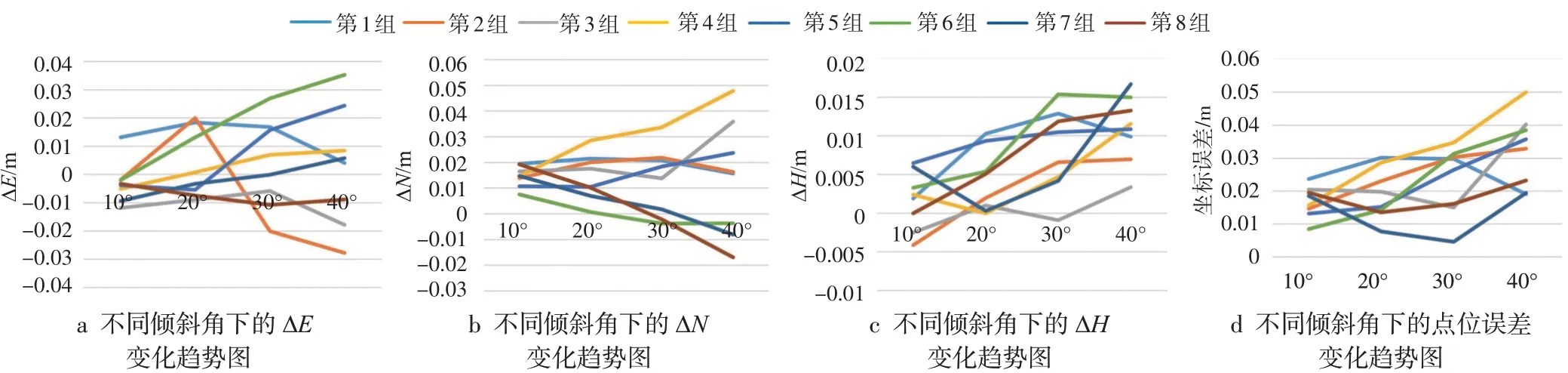
圖4 不同傾斜角下的ΔE、ΔN、ΔH以及坐標誤差值變化趨勢圖

2）當傾斜角小于30°時，點位誤差會出現波動的情況；但當傾斜角大于30°之后，點位誤差基本不會再發生波動，而是穩定地隨傾斜角度的增大而增大，但變化方向并不固定，在對中桿向不同的方向進行傾斜時，誤差值會朝正負不同的方向增加。

3）在E、N、H3個方向上進行比較時可以看出，在進行傾斜測量時，水平的2個方向上的誤差值更大，垂直方向上的誤差基本只有水平方向的一半左右。

2）方位角對傾斜補償精度的影響。由圖5可見，對于ΔE值來說，在不同的傾斜角下其在各個方向上的變化趨勢是非常類似的，在方位角從第3組狀態轉向第6組狀態的過程中，ΔE值不斷向正方向增加；當繼續向第7、8組狀態進行偏轉時，ΔE值開始向負方向變化；而繼續偏轉超過第8組狀態之后，ΔE值又開始轉為向正方向變化；但繼續偏轉達到第3組狀態之后，便又向負方向增加，并且可以明顯看出，向正負方向進行變化時，傾斜幅度越大變化幅度就越大。

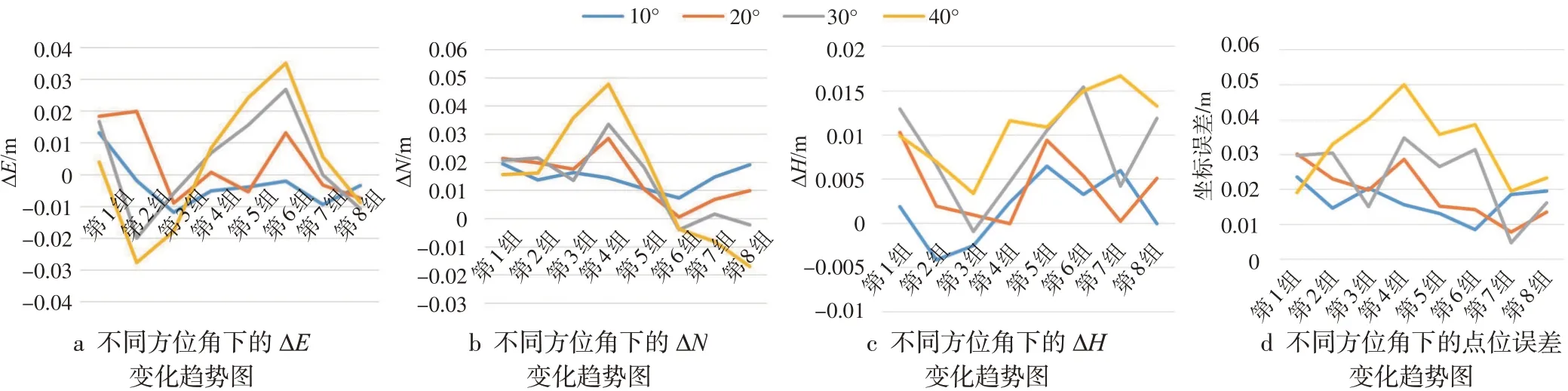
圖5 不同方位角下的ΔE、ΔN、ΔH以及坐標誤差值變化趨勢圖

對于ΔN值來說也是如此，在不同的傾斜角下，其在各個方向上的變化趨勢也是類似的，在方位角從第3組狀態轉向第4組狀態的過程中，ΔN值向正方向增大；方位角從方向4偏轉到方向6時，ΔN值又向負方向變化；隨后，隨著方位角的繼續偏轉，ΔN值又緩慢向正方向變化。

而在ΔH值上的情況有一些差別，總體而言化趨勢是類似的，都是隨著方位角的偏轉，其誤差值逐漸變小，繼續偏轉達到第3組狀態之后又逐漸升高，到達第5、6組狀態后其誤差值又慢慢回落；但是在偏轉超過第7組狀態且傾斜角處于20°和30°時，其ΔH值復又開始增大；但在傾斜角處于10°和40°時，其ΔH值是逐漸減小的。

綜合來看點位誤差的變化，在方位角偏轉超過第3組之后且傾斜角大于10°的狀態下，整體的變化趨勢還是十分類似的，呈現了先增大在波折減小的變化趨勢；而當傾斜角在10°時，其整體變化幅度很小，呈現了向正負方向不斷波動的變化趨勢。

方位角對于傾斜補償精度影響總結如下：

1）在對中桿處于不同組別的狀態下進行傾斜測量時，誤差值在E、N、H3個方向上的變化規律是不相同的，但在同一方向內，其變化趨勢基本是一致的。

2）ΔE值在對中桿處于第6組狀態時最大，處于第3、7、8組狀態時最小；ΔN值在對中桿處于第4組狀態時最大，處于第6、7、8組狀態時最小；ΔH值在對中桿處于第6組狀態時最大，處于第7組狀態時最小；綜合點位誤差在對中桿處于第4組狀態時最大，處于第7組狀態時最小。

3）在本次實驗中，明顯可以看出當對中桿處于第4、5組狀態時誤差值較大，而處于第7、8組傾斜時其傾斜補償效果明顯更好，考慮當其方位角不同時，可見星數以及衛星的分布不同也會對其測量精度造成影響。

3 結論

1）帶有MEMS慣性傳感元件的徠卡GS18傾斜機在進行RTK傾斜測量時，能夠進行高精度的傾斜補償，克服在墻角、電線桿等需要進行偏心觀測或是在溝渠、管線等難以進行普通RTK測量的環境下的測量困難，增強了實用性，同時省去了調平水準氣泡的環節，提高了測量工作的效率。

2）隨著對中桿傾斜角的增大，傾斜補償的精度受到影響，點位誤差存在增大的趨勢。儀器傾斜方位角的不同，天空的衛星分布情況對儀器測量精度也有一定的影響。在測量時應該盡可能減小傾斜角，盡量保證傾斜角小于30°，以保證精度。