尋求促進(jìn)學(xué)生深度學(xué)習(xí)的策略
——以《商中間或末尾有0 的除法（一）》為例

文|張紹華 張冬梅（特級教師）

“數(shù)的運算”是小學(xué)數(shù)學(xué)學(xué)科的核心內(nèi)容，而“兩、三位數(shù)除以一位數(shù)”是其中的重要組成部分。它在整數(shù)除法中承上啟下：既是表內(nèi)除法的自然延伸，更是除數(shù)是兩位數(shù)乃至更多位數(shù)除法的基礎(chǔ)，它開啟了學(xué)生對于除法計算法則的探索和理解。而商中間或末尾有0 的除法又是其中的難點內(nèi)容，不僅難在對“0”的處理上，還會由此導(dǎo)致對原先計算法則的混亂：“漏掉0”和“沒有逐位除”常常互為因果，導(dǎo)致出錯。

這樣一個具有挑戰(zhàn)性的學(xué)習(xí)主題，學(xué)生需要在教師引領(lǐng)下積極參與，不斷深入觸及計算的算理和算法，經(jīng)歷認(rèn)知結(jié)構(gòu)逐步完善的數(shù)學(xué)學(xué)習(xí)過程，實現(xiàn)深度學(xué)習(xí)。王琛老師的《圖式學(xué)習(xí)：理法交融的新探究》（下稱“設(shè)計一”）、張冬梅老師的《把握學(xué)生數(shù)學(xué)現(xiàn)實 促進(jìn)學(xué)生深度學(xué)習(xí)》（下稱“設(shè)計二”），這兩篇設(shè)計以“主線問題”聚焦核心任務(wù)；以“憤悱”狀態(tài)引發(fā)深度探究；以“對比”技術(shù)完善認(rèn)知結(jié)構(gòu)，為尋求小學(xué)數(shù)學(xué)“深度學(xué)習(xí)”的策略提供了鮮活可鑒的案例。

策略一：以“主線問題”聚焦核心任務(wù)

在平時的課堂教學(xué)中，我們經(jīng)常看到有些教師習(xí)慣對知識點進(jìn)行零敲碎打，限制學(xué)生的思維拓展，難以提高學(xué)生的學(xué)習(xí)興趣，更不用談深度學(xué)習(xí)了。要想有效改變這一現(xiàn)狀，使學(xué)生的數(shù)學(xué)學(xué)習(xí)更具張力，學(xué)習(xí)思維更具深度，教師要充分發(fā)揮自身的能動性與創(chuàng)造性，理性而深刻地把握教學(xué)內(nèi)容，以“主線問題”成就學(xué)習(xí)內(nèi)容的結(jié)構(gòu)化，幫助學(xué)生實現(xiàn)深度學(xué)習(xí)。

1.以“主線問題”構(gòu)建連貫性的知識體系。

“設(shè)計二”的“主線問題”是以“自主出題”的方式呈現(xiàn)的。

內(nèi)容雖然簡短，信息量卻很大，作為“主線問題”，它將貫穿于整節(jié)課的學(xué)習(xí)中，明確了整堂課的研究主線，為深度學(xué)習(xí)創(chuàng)造了時空。首先，這里的“寫一寫”，學(xué)生需要出一道三位數(shù)除以一位數(shù)的算式，全班幾十位學(xué)生，有的出了已經(jīng)學(xué)過的一般情況；也有的會出到今天需研究的商中間或末尾有0 的情況（因某一位上是“0除以一個數(shù)”）；還會出到后面要研究的商中間或末尾有0 的情況（因某一位上“不夠商1 要商0”）。也就是說，學(xué)生的出題可能會囊括三位數(shù)除以一位數(shù)的所有情況，構(gòu)成了不僅是這節(jié)課，更是這個單元的核心學(xué)習(xí)素材。

接下來的“算一算”，如果學(xué)生算的是已學(xué)過的豎式，不僅是復(fù)習(xí)鞏固，更是為今天的學(xué)習(xí)提供基礎(chǔ)：從高位算起，算到哪一位商就寫在那一位上。今天的學(xué)習(xí)內(nèi)容雖是除法計算中的特殊情況，但也必須遵循上述法則，才能正確處理“0”的問題。如果學(xué)生算的是商或末尾有0 的豎式，那么他將自覺進(jìn)入探究階段，為處理好這個“0”尋求依據(jù)，合理表征。若是在探究的過程中遇到困難，則會自動進(jìn)入第三個環(huán)節(jié)“議一議”。

2.以“主線問題”關(guān)照“心智模式”，促進(jìn)思維進(jìn)階。

“設(shè)計一”的“主線問題”是以“圖式學(xué)習(xí)單”呈現(xiàn)的。

在《圖式學(xué)習(xí)單》中，清楚地看到課堂學(xué)習(xí)分為四個階段：自學(xué)與探究、反思與提問、歸納與總結(jié)、拓展與聯(lián)想。

在“自學(xué)與探究”階段，學(xué)生將嘗試解決新問題，或正確或錯誤，或順利或遇阻，探究成功與否在這里不是最重要的，重要的是積累了探究的經(jīng)驗。帶著這些經(jīng)驗進(jìn)入到“反思與問題”階段：有困難的說困難，有錯誤的共反思，一個小組的同學(xué)一起交流、智慧碰撞，最終在磕磕碰碰中達(dá)成一定的共識。接下來的“歸納與總結(jié)”很重要，在這個階段里要提煉出今天學(xué)習(xí)的重點：商中間或末尾有0 的計算方法，并與原先的舊知相互關(guān)聯(lián)，完善“除數(shù)是一位數(shù)的除法計算法則”這一認(rèn)知結(jié)構(gòu)。最后還要再往前跨一步：“拓展與聯(lián)想”，舉一反三，認(rèn)知遷移，發(fā)現(xiàn)新問題等等。

可以看出，這份學(xué)習(xí)單不僅可以用于這節(jié)計算教學(xué)課，也可以用于其他課型中。其中的“自學(xué)與探究”“反思與提問”“歸納與總結(jié)”“拓展與聯(lián)想”板塊為學(xué)生的學(xué)習(xí)提供了程序指引，成為學(xué)生實現(xiàn)深度學(xué)習(xí)的腳手架。

我們看到，在王老師的課堂上，學(xué)生的認(rèn)知結(jié)構(gòu)構(gòu)建在心智模式基礎(chǔ)之上，學(xué)生第一步是接收信息，然后在腦海中形成初步的印象；第二步是感悟并體驗知識，這有助于調(diào)動學(xué)生的心理能量進(jìn)行學(xué)習(xí)；第三步則是思考和探索，向高階思維不斷地升級進(jìn)化，從而產(chǎn)生認(rèn)知結(jié)構(gòu)，形成獨具個性化的方法論。

策略二：以“憤悱”的狀態(tài)引發(fā)深度探究

在這節(jié)課的學(xué)習(xí)中，學(xué)生多次遭遇認(rèn)知沖突，產(chǎn)生“憤悱”。每一次“憤悱”的即時狀態(tài)都被教師及時捕捉，引發(fā)了學(xué)生的深度探究。以教師對文本和學(xué)生的分析理解，結(jié)合課堂上的生成，本節(jié)課的學(xué)習(xí)，學(xué)生必將出現(xiàn)以下幾次“憤悱”狀態(tài)：

1.0除以一個數(shù)究竟得幾。

這里包含兩個要素，一是除數(shù)的范圍（除數(shù)為何不能為0），二是結(jié)果的依據(jù)（為什么結(jié)果是0）。

“設(shè)計二”中，關(guān)于這個問題，第一次“憤悱”是在討論609÷3的過程中，有學(xué)生提出“0÷3”為什么等于0？由于此時主線任務(wù)是探尋商中間有0 除法的算理算法。再則，此“憤悱”并非三言兩語說得清。所以教師將這個重要“插曲”暫且擱下，待日后再重點解決。等到例9 完全解決了，再來逐步細(xì)究。引導(dǎo)學(xué)生從“0 除以3 為什么得0”→“0 除以別的數(shù)也等于0 嗎”→“0 可以除以0嗎”，層層遞進(jìn)開展討論，學(xué)生通過舉例子（運用除法的意義）、想乘法（運用乘除法的聯(lián)系），最終得出結(jié)論：0 除以任何不是0 的數(shù)都等于0。

“設(shè)計一”中，是把這個問題先行解決。由6÷3=2，自然地將除法的意義用于解釋0÷3=0；再啟發(fā)學(xué)生在更豐富的情境表征中理解0 除以一個數(shù)的意義；最后引導(dǎo)學(xué)生觀察算式，用不完全歸納得出結(jié)論。

兩位教師都根據(jù)學(xué)生“憤悱”的程度拿捏分寸，在“設(shè)計一”中，學(xué)生對于0 是否可以做除數(shù)，沒有提出疑問，所舉例子也都是非零除數(shù)，教師也就沒有深究。“設(shè)計二”中，學(xué)生質(zhì)疑到“0÷0”的問題，教師就放開讓學(xué)生討論，做到知其然更知其所以然。而非零被除數(shù)除以0 的現(xiàn)象，學(xué)生也沒有提及，教師同樣順其自然。

2.商中間的0 如何處理。

這里同樣包括兩個要素，一是算理（0 除以任何不是0 的數(shù)都等于0），二是算法（被除數(shù)十位上0 除以除數(shù)得0，在商的十位用0占位）。

●“設(shè)計二”中，我們可以看到三個細(xì)節(jié)。

第一個細(xì)節(jié)，在學(xué)生計算自己出的題目并小組交流時，教師發(fā)現(xiàn)：他們小組交流了很長時間，他們到底遇到了什么困難？這個小組一定是在答案或格式上存在爭議，所以此時全班一起來研究“609÷3”順理成章。

第二個細(xì)節(jié)，當(dāng)學(xué)生對這題已經(jīng)各有想法，并得到了正確解法后，在討論中，有學(xué)生質(zhì)疑：“（指著商中間的0）這個0 是哪里來的？豎式中看不出來。”“其實就是用十位上0 除以3 得0，只是省略了過程，直接寫商是0。”在這一問一答中，學(xué)生明白了算理，同時也讓學(xué)生在兩種豎式寫法的比較中，獲得這種簡便寫法的依據(jù)。

第三個細(xì)節(jié)，是當(dāng)商中間或末尾有0 的除法都討論完了，教師又來了個回馬槍：“還記得一開始這道大家認(rèn)為做錯的題嗎？那現(xiàn)在大家看看，錯誤的原因在哪里？”第一次面對這個錯誤，學(xué)生只是用估算來確定它錯了，而這次是在積累了筆算經(jīng)驗后，剖析錯誤的原因，強(qiáng)化了“逐位除”的重要性。

●“設(shè)計一”中，也可以看到兩個細(xì)節(jié)。

第一個細(xì)節(jié)在“反思小結(jié)”環(huán)節(jié)：“我們認(rèn)為在計算之前先估一估也很重要，可以知道商是幾位數(shù)，這樣不容易錯。”“0 除以3 雖然很簡單，但是很容易會在商上漏寫0，這個0 也很重要，是要占位的。”“我也要提醒大家商中間的0 不能遺漏。我們還可以在計算后用乘法進(jìn)行驗算。”

這些學(xué)生的反思恰恰是部分學(xué)生存在的“憤悱”，在互動中，學(xué)生再次明確要處理好商中間的0，并且可以用估算和驗算的方法幫助自己。

第二個細(xì)節(jié)是在“基礎(chǔ)拓展”環(huán)節(jié)，學(xué)生特別關(guān)注了一道題：“800÷5，被除數(shù)末尾有兩個0，商的末尾為什么只有一個0？”這個學(xué)生的“憤悱”真實反映了部分學(xué)生的錯誤認(rèn)知：被除數(shù)哪位是0，商的那一位就是0。在這次生生互動中，學(xué)生又一次梳理了筆算法則：一位一位地除，除到哪一位有余數(shù)，就和下一位上的數(shù)合起來繼續(xù)除；如果遇到了0 除以除數(shù)，那就得0。

從上述的片斷中可以看出，有時學(xué)生對一個問題的“憤悱”不是一次就能解決的，需要在不斷進(jìn)階的思考、探究中撥云見日。

3.商末尾的0 如何處理。

有了“商中間有0”的學(xué)習(xí)經(jīng)驗，關(guān)于“商末尾的0”，其算理和算法可以類比遷移。因此兩位教師并未用濃墨，卻又都不乏點睛之筆。

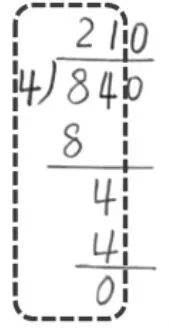
比如“設(shè)計二”中，“大家看看第二種方法的這個部分，其實是在算？”教師的一句“其實是在算”引發(fā)了學(xué)生對之前學(xué)習(xí)的整百整十?dāng)?shù)除以一位數(shù)的口算算理的聯(lián)系，進(jìn)一步理解末尾商0 的道理及方法簡化的依據(jù)。

“設(shè)計一”中，當(dāng)學(xué)習(xí)進(jìn)入到“反思與提問”模塊的“發(fā)現(xiàn)問題、解決問題”環(huán)節(jié)，學(xué)生主動提出關(guān)于“商末尾有0”的“憤悱”，接下來的研究也就自然而然拉開序幕。

從以上片斷中，我們可以有所啟示，“設(shè)計二”關(guān)于“商末尾有0”的“憤悱”是教師問出來的，而“設(shè)計一”中是學(xué)生主動提出的。其實，面對幾十個學(xué)生的學(xué)習(xí)共同體，“憤悱”隨處可見，有時學(xué)生能夠主動提出，固然是好；但有時學(xué)生真的“憤”到自己都表達(dá)不出甚至意識不到，這時教師的引導(dǎo)就尤為重要了。

4.因某一位上“不夠商1 要商0”的情況，如何處理。

雖然這不是今天的學(xué)習(xí)內(nèi)容，但不代表學(xué)生不會遇到、想到，無需回避，只是放到下節(jié)課再“啟”，留著念想，也是學(xué)習(xí)的一大快樂。

在“設(shè)計二”中，正因為課始教師讓學(xué)生“自主出題”，極有可能學(xué)生會出到此類型，于是教師將這個生成的資源，用來激勵學(xué)生繼續(xù)學(xué)習(xí)與探究的興趣：“老師在同學(xué)們自主出題的過程中，還找到了這道題（出示“432÷4”）。他們小組也沒能正確計算。這道題又有什么新的挑戰(zhàn)呢？讓我們一起期待下節(jié)課的研究。”

“設(shè)計一”中，則是在最后的“拓展與聯(lián)想”模塊中，學(xué)生照例要想一想：有哪些收獲，還想到什么？可以看出，王老師的學(xué)生關(guān)于《圖式學(xué)習(xí)單》的使用已是常態(tài)，學(xué)生其間也許會指向“不夠商1要商0”的除法。

策略三：用“對比”的技術(shù)促進(jìn)認(rèn)知結(jié)構(gòu)的完善

對比是教學(xué)中的常用手段，對比不僅讓學(xué)生看到了相同或是不同的現(xiàn)象，更促進(jìn)了學(xué)生認(rèn)知結(jié)構(gòu)的進(jìn)一步完善。

兩位教師不約而同用“對比”的技術(shù)促進(jìn)深度學(xué)習(xí)，促進(jìn)認(rèn)知結(jié)構(gòu)的完善。

1.深究算理與算法。

在探索商中間有0 除法的計算方法時，兩位教師都明確指出對比要求，在“設(shè)計二”中，教師要求比一比這兩種豎式。在比較中，學(xué)生首先從形式上看到了不同：第一種方法每一步都算，算到十位0÷3=0，所以在商的十位寫0，而第二種方法把這步省略了。可比著比著，學(xué)生又比出了兩者本質(zhì)上的相同：兩種方法其實是一樣的，只是第二種方法把十位那步“想在心里”了。學(xué)生明晰了：不寫出來不代表不算、不想，這樣使得學(xué)生不僅在形式上看到了第二種方法的簡潔，更在對比中看到了它的合理性。

“設(shè)計一”中，在《圖式學(xué)習(xí)單》的“自學(xué)與探索”環(huán)節(jié)中，是讓學(xué)生“用自己喜歡的方式算一算”，所以學(xué)生并非只限于豎式，而是呈現(xiàn)了各種方法，有用口算方法的，有畫圖的，有用不同豎式的。待學(xué)生把各自的方法解釋清楚后，教師又組織學(xué)生對這些方法進(jìn)行對比。學(xué)生在互動中越發(fā)清楚地看到，其實這些方法的算理都是一樣的，還有學(xué)生說借助畫圖法，可以把其他方法都解釋清楚。

對比使得學(xué)生對豎式的認(rèn)知不只是形式上清晰，更是算理和算法的清晰。

2.溝通知識間的聯(lián)系。

在商中間、末尾有0 除法都研究完以后，王老師組織學(xué)生對比剛剛研究的“306÷3、480÷4 和350÷5”這三個豎式；而張老師的步子就更大了，組織學(xué)生同時對比了五個豎式。學(xué)生都是先站在今天課堂的視角看現(xiàn)象：有的是商中間有0，有的是商末尾有0；今天的除法商里面有0，以前的除法商里面沒有0；可以用估算和驗算避免漏0；被除數(shù)中有0，商里不一定有0……真正構(gòu)建了對新學(xué)內(nèi)容的認(rèn)知。后來，學(xué)生又站在本單元的視角意識到：今天和以前一樣，從高位算起，一位一位地除，算到哪一位，就在那一位上寫商。這是將新的認(rèn)知納入到原有的認(rèn)知結(jié)構(gòu)中，對于除數(shù)是一位數(shù)的除法形成了更上位、更完善的認(rèn)知結(jié)構(gòu)。

總之，在“設(shè)計一”中，讓我們更多地看到，把握了學(xué)生的數(shù)學(xué)現(xiàn)實，也就是我們所說的切實做好學(xué)情分析，才能引著學(xué)生走得更遠(yuǎn)，促進(jìn)深度學(xué)習(xí)。而“設(shè)計二”中為我們提供了有效的實現(xiàn)深度學(xué)習(xí)的策略：《圖式學(xué)習(xí)單》，其中的四大模塊就是學(xué)生走向深度學(xué)習(xí)的基本階梯。