海上浮式風電機組變槳距自抗擾控制策略研究

王詩琪,杜雪松,朱才朝,譚建軍,,宋朝省,劉 斌

(1.重慶大學 機械傳動國家重點實驗室，重慶 400044；2.中國船舶重工集團海裝風電股份有限公司，重慶 401121)

海上浮式風電機組適用于獲取深、遠海域(水深大于60 m)風能資源[1-2]，但在運行過程中浮式風機在風浪聯合作用下的六自由度運動會對浮式風機的性能產生很大影響，導致風機的功率產生周期性波動[3]。這是因為隨機風、浪載荷的聯合激勵，會引起平臺和塔架的傾斜運動[4]，使整個機組的空間運行姿態產生顯著變化[5]，進而改變不同槳距角下葉片不同徑向位置處的入流風速，增加發電功率波動。因此，研究海上浮式風電機組變槳距控制對保持輸出功率穩定具有重要的意義。

目前，國內外學者針對風電機組變槳距控制開展了大量深入研究。Colombo等[6]提出了將葉片槳距角作為控制變量輸入的滑膜控制方法，并驗證了其閉環收斂性。Yin等[7]提出了風電機組變槳距自適應魯棒控制策略，提高了系統的魯棒性。Civelek等[8-10]通過將模糊控制與變槳距控制結合，實現了風電機組恒功率控制。苑晨陽等[11-12]利用人工蜂群算法對風電機組變槳距PID控制器參數進行優化，有效地降低了發電功率和風輪轉速波動。雖然上述控制方法在一定程度上可以改善風電機組變槳距控制性能，但是在實際控制過程中由于難以獲取精確的控制模型與系統參數，應用局限性大。自抗擾控制(active disturbance rejection control, ADRC)[13-14]不依賴于被控系統精確的數學模型，對控制品質和控制精度有顯著提高。目前，已有學者將ADRC應用于風電機組變槳系統[15-18]。然而，目前變槳距ADRC控制研究都將風電機組進行了簡化，未考慮風電機組氣動力、水動力、結構彈性和變槳距控制之間耦合，并且目前變槳距ADRC控制器的參數整定仍依靠專家經驗，造成變槳距ADRC實際應用受限。

綜上所述，海上浮式風電機組模型復雜，難以獲取精確的控制模型和系統參數，采用不依賴精確數學模型的變槳距ADRC策略可以有效提高控制精度。同時，考慮到ADRC需要整定的參數過多且不利于在實際工程中應用，將ADRC簡化為線性自抗擾控制(LADRC)[19]，降低了調試難度，更具工程實用性。

1 海上浮式風電機組變槳距運行原理

如圖1所示，海上浮式風電機組整機主要包括葉片、塔架、傳動鏈、機艙、浮動平臺以及錨鏈等。葉片將風能轉換為機械能，通過傳動鏈傳遞到發電機并轉化為電能[20]。海上浮式風電機組整機由浮動平臺提供支撐，錨鏈約束其空間運動范圍。在風、浪載荷聯合激勵下，海上浮式風電機組整機將產生6個方向的剛體運動。表1所示為某5 MW級海上浮式風電機組整機結構參數。

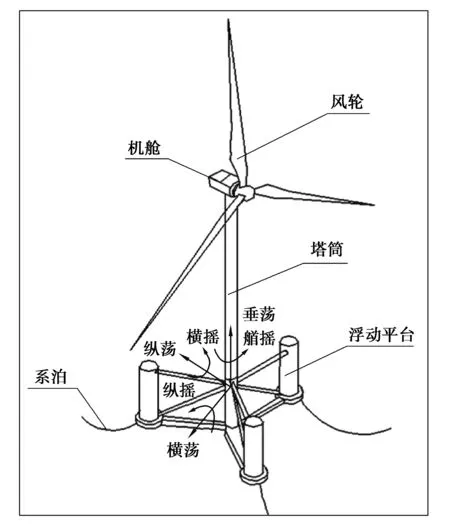
圖1 某5 MW級海上浮式風電機組整機結構Fig. 1 Structure of a 5 MW offshore floating wind turbine

表1 某5 MW級海上浮式風電機組整機參數

根據切入、切出和額定風速大小可將變槳距運行分為低風速階段、過渡階段和高風速階段。圖2和圖3分別為不同風速下發電功率和槳距角變化曲線。

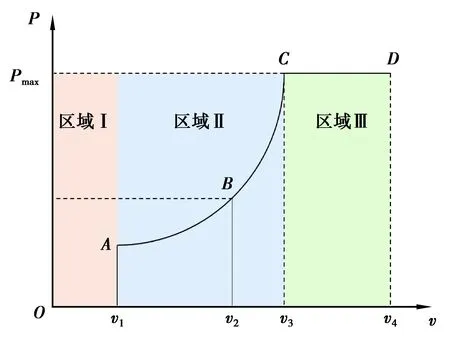
圖2 不同風速下發電功率曲線Fig. 2 Power curve with different wind speeds

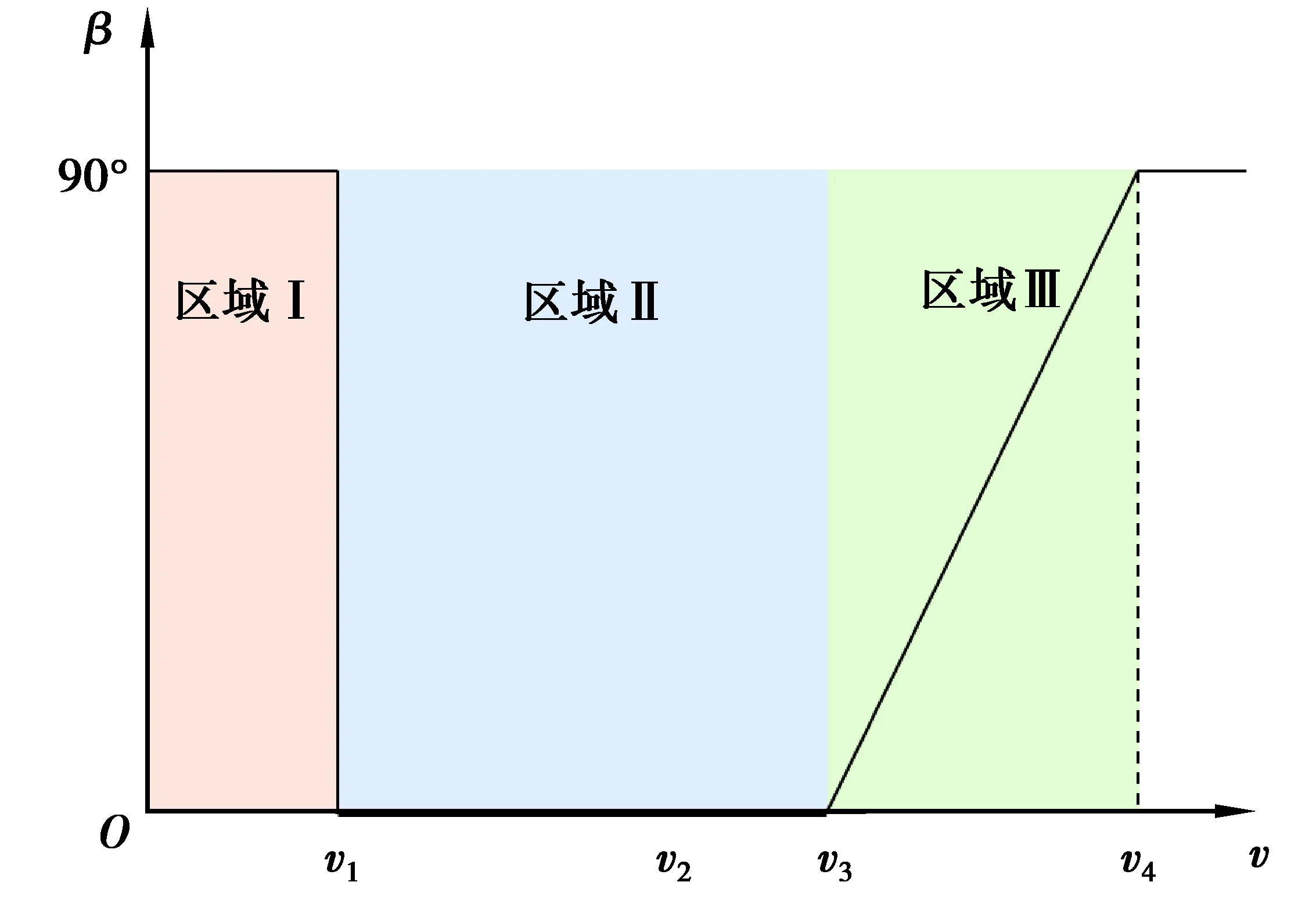
圖3 不同風速下槳距角曲線Fig. 3 Pitch angle curve with different wind speeds

當風機運行于低風速階段(區域I)時，葉片槳距角保持在90°不變；當風速達到切入風速v1時，變槳執行機構將槳距角控制在零附近，使風輪獲得較大的啟動轉矩；當風速低于額定風速v3時，維持槳距角固定不變，通過調節風輪轉速使其工作在最佳葉尖速比處；當風速高于額定風速v3的情況下，變槳執行機構采用改變槳距角的策略，使系統的輸出功率穩定于額定功率處。

2 海上浮式風電機組氣彈水控耦合系統動力學模型

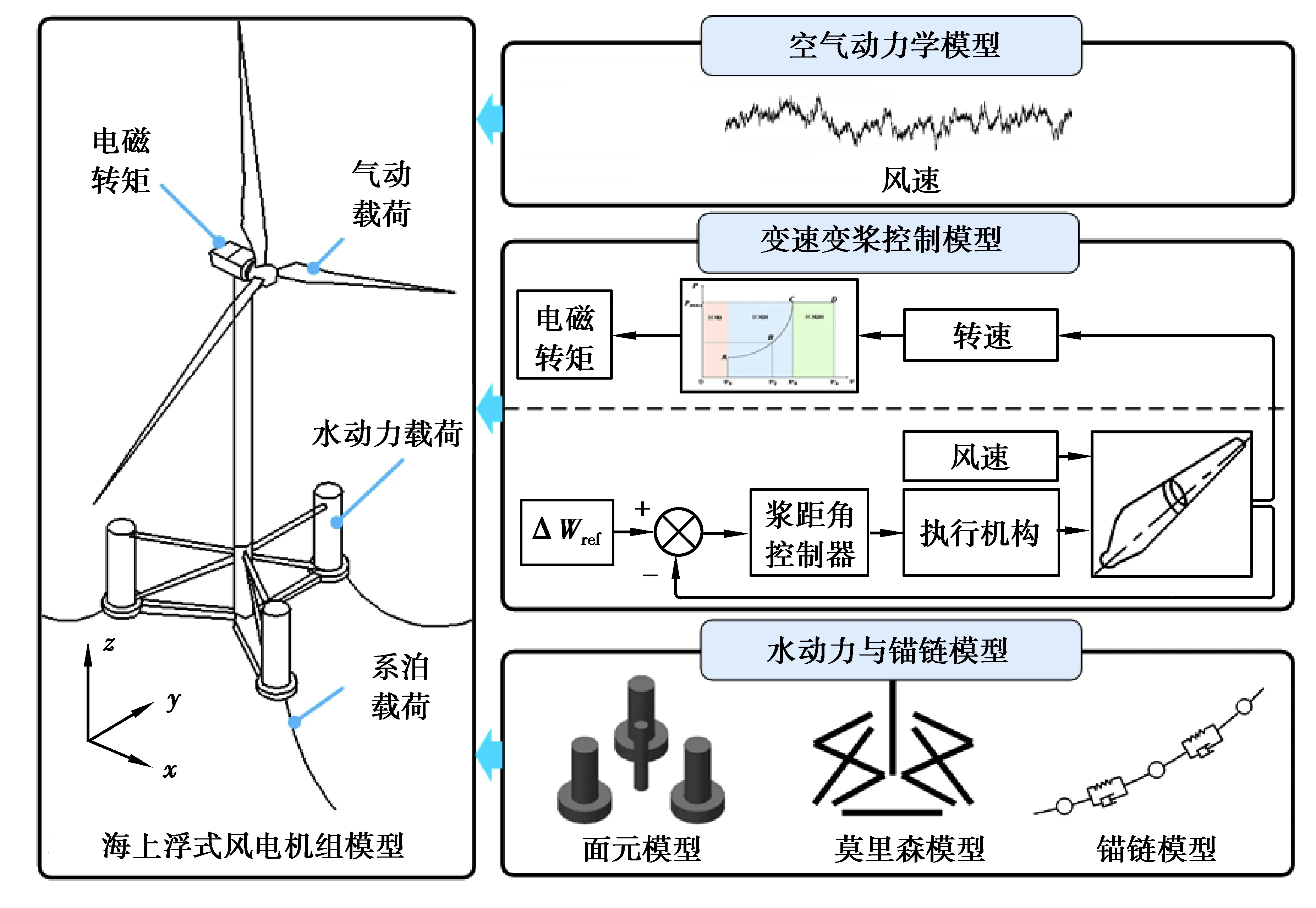
圖4 海上浮式風電機組耦合模型Fig. 4 Coupling model of an offshore floating wind turbine

2.1 空氣動力學模型

將葉片沿展向分成若干葉素單元，通過對作用在各個葉素的氣動力沿展向積分，得到作用在整體葉片上的氣動力載荷，如圖5所示[23]。

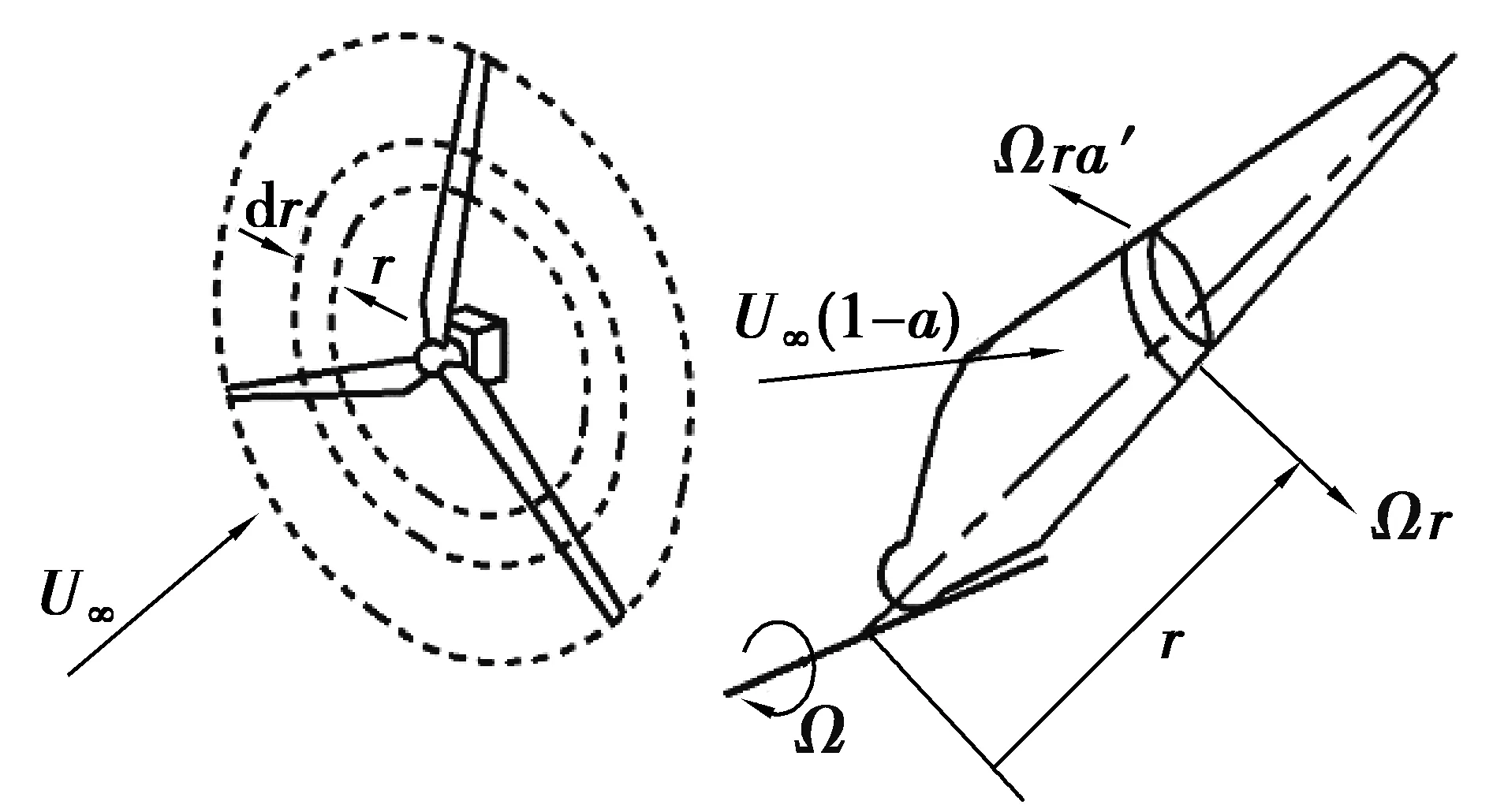
圖5 葉素動量理論示意圖Fig. 5 Diagram of blade element-momentum theory

利用葉素理論計算環形區域中葉素所產生的推力和轉矩

(1)

(2)

式中：dT為環形區域中的葉素推力；dQ為環形區域中的葉素轉矩；B為葉片數目；ρ為流體密度；c為翼型弦長；φ為入流角；v為葉素單元速度；CL和CD為葉素升力和阻力系數；r為葉素局部半徑。

最后利用動量定理計算環形區域的葉素所產生的推力和轉矩

dT=4πrρU∞2(1-a)adr，

(3)

dQ=4πr3ρU∞ω(1-a)a′dr。

(4)

式中:U∞為垂直于風輪平面的來流風速；a和a′為軸向和切向誘導因子；ω為風輪轉速。

通過結合公式(1)～(4)，與二維翼型升阻特性參數，通過數值迭代可以得到風機葉片氣動轉矩與推力。

2.2 結構動力學模型

風輪、傳動鏈、機艙、塔架、浮式平臺和錨鏈耦合系統的動力學方程為[24]

(5)

2.3 水動力學模型

如圖6所示，將浮式平臺中浮筒定義為大尺度構件，建立面元模型；將平臺連桿定義為小尺度構件，建立莫里森模型[23]。

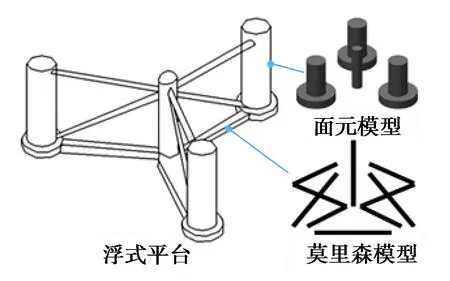
圖6 浮式平臺模型Fig. 6 Floating platform model

在面元模型中，利用三維勢流理論計算波浪力,即

(6)

式中：FWi為第i自由度下的波浪力；φi為入射波的速度勢；S為面積；ni為第i自由度下浮體表面單位外法方向的向量；φd為繞射波速度勢。

在莫里森模型中，利用莫里森公式計算波浪力,即

(7)

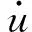
如圖7所示，采用集中質量法建立錨鏈系統模型，錨鏈由連接節點和彈簧阻尼系統表示[23]。

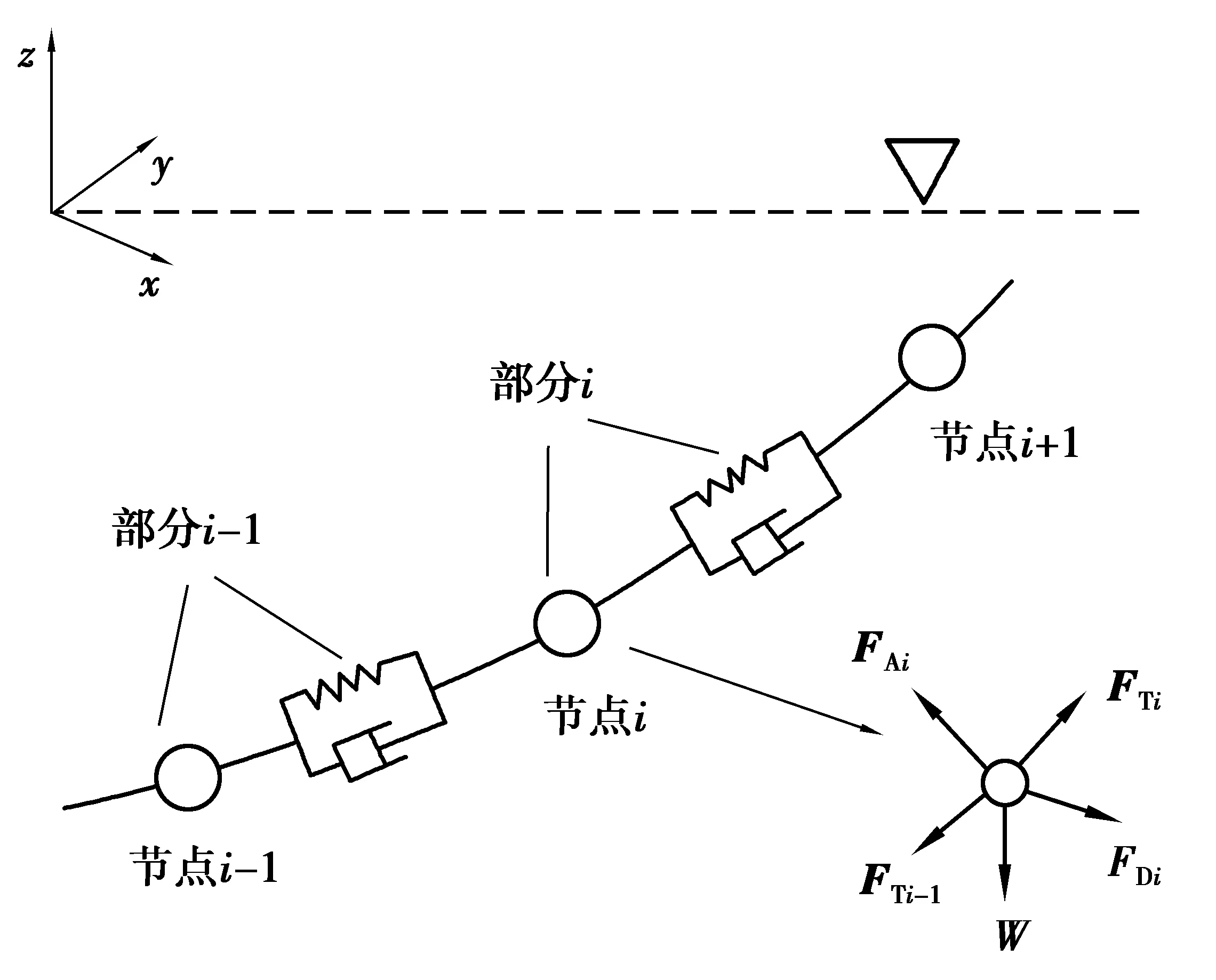
圖7 錨鏈受力分析Fig. 7 Force analysis of anchor chain

錨鏈動力學方程為

(8)

(9)

FAi=ρCMV(-ai)，

(10)

式中：Mi為節點的質量；ai為節點i的加速度向量；FTi為元素i的張力向量；FTi-1為元素i-1的張力向量；FDNi為節點i的流體法向力；FDTi為節點i的流體切向力；FAi為節點i的流體慣性力；Wi為節點i的重力。

2.4 變槳控制模型

如圖8所示，風電機組變槳距控制主要通過變槳執行機構實現，可以將其等效為一階慣性環節，其傳遞函數為

(11)

式中：β為實際槳距角；βr為設定槳距角；τ為變槳執行機構時間常數；s表示時間。

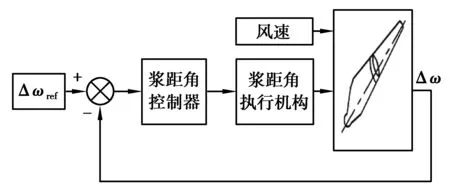
圖8 變槳控制圖Fig. 8 Pitch control diagram

2.5 海上浮式風電機組整機氣彈水控全耦合動力學模型

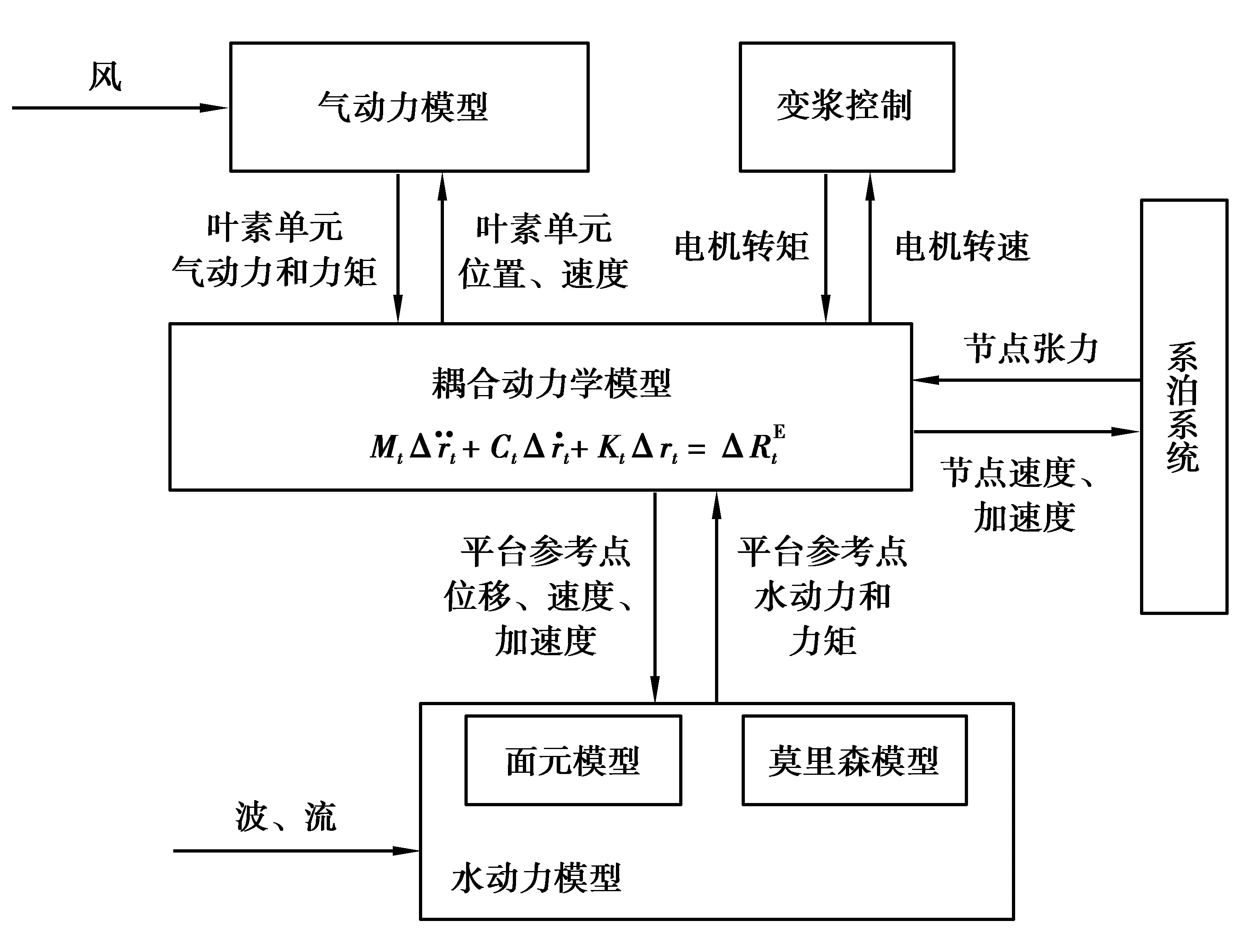
圖9 浮式風電機組整機氣彈水控全耦合動力學模型Fig. 9 Full coupled block diagram of gas-elasto-water-control dynamics of a floating wind turbine

3 海上浮式風電機組變槳距自抗擾控制器設計

圖10 變槳距LADRCFig. 10 Pitch LADRC

3.1 線性擴張狀態觀測器設計

(12)

式中：Tair為風輪轉矩；Tgen為發電機的電磁轉矩；J為風輪轉動慣量；ω為風輪轉速。

選定風電機組在額定功率處且對應的風能利用率cp最高處作為平衡點，對傳動系統進行線性化處理，如式(13)所示。

(13)

式中：Tr為發電機電磁轉矩；Tro為平衡點處發電機電磁轉矩；β為槳距角；v為風速；h為展開高次項。

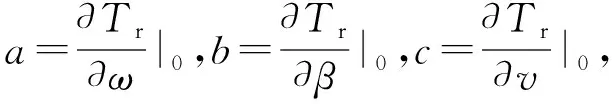
Tr-Tro=aΔω+bΔβ+cΔv+h，

(14)

以Δω為變槳距LADRC輸入，結合式(14)可得

(15)

考慮到槳距角的動態特性，可得

(16)

式中Δβr為槳距角控制給定值。

因此，式(15)可轉化為

(17)

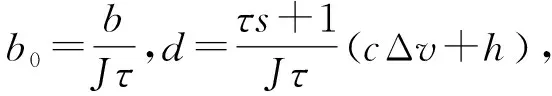
(18)

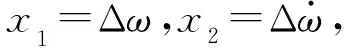
(19)

根據自抗擾控制理論，基于式(19)可得線性擴張狀態觀測器狀態方程為

(20)

式中l1，l2，l3為待調節參數。

3.2 狀態反饋控制率設計

采用如下狀態反饋控制率[25]

(21)

式中r為參考信號。

最終控制率為

(22)

根據式(12)～(22)設計變槳距LADRC控制器，其控制率為

(23)

式中k1，k2，b0為待調節參數。

3.3 控制器參數整定

海上浮式風電機組變槳距自抗擾控制器的帶調節參數為l1，l2，l3，k1，k2，b0。考慮到海上浮式風電機組機構的復雜性，提出帶寬整定法和BP神經網絡整定法對LADRC的待調整參數進行整定，以提高抗擾性能和實用性。

3.3.1 帶寬整定法

由式(23)可知，LADRC有6個參數需要整定，因此對式(23)進行拉式變換，得到系統的閉環傳遞函數[19]

(24)

其中

A1(s)=s3+(l1+k2)s2+(l1k2+l2)s，

(25)

A2(s)=k1s3+(l3+l2k2+l1k1)s2+(l3k2+l2k1)s+l3k1。

(26)

令

(27)

(28)

故系統的單位階躍響應為

y(t)=1-(1+ωct)e-ωct。

(29)

將式(27)改寫為

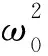
(30)

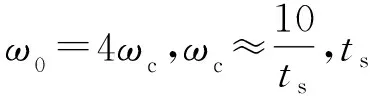
綜上所述，帶寬整定LADRC的方法是：先確定系統要求的調節時間ts，然后根據ts，調整ωc和ω0的值，再根據式(27)調整l1，l2，l3，k1，k2的值，最后逐漸增大b0值，保證調節時間和超調量滿足系統要求。

3.3.2 BP神經網絡整定法

采用基于BP神經網絡的PID控制方法[26]，將神經網絡輸出層的輸出等效為二階LADRC參數[27]，即將PID參數轉化為二階自抗擾控制參數，如式(31)所示。

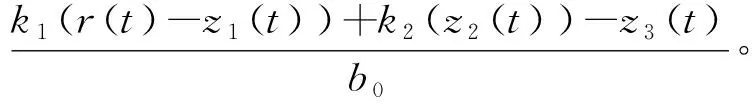
(31)

由式(31)可知，二階LADRC包括比例項(k1/b0)(r(t)-z1(t))、微分項(k2/b0)z2(t)以及擾動估計及補償項(1/b0)z3(t)，實際上就是P+I+D的組合，但沒有直接采用輸出導數和積分，而是利用擴張狀態觀測器直接進行估計。因此，文中采用基于BP神經網絡的PID控制方法對LADRC參數進行整定。

采用3層BP神經網絡7-8-3，BP神經網絡LADRC算法如圖11所示。

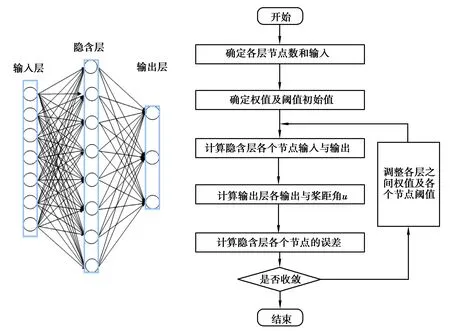
圖11 BP神經網絡流程圖Fig. 11 Flow chart of BP neural network

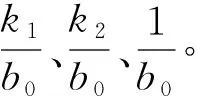
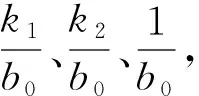
4 仿真結果與分析

利用FAST建立某5 MW級海上浮式風電機組的空氣動力學模塊、結構動力學模塊和水動力學模塊。LADRC模塊則利用Simulink搭建，通過Level-2 S-Function調用FAST動態鏈接庫，實現與FAST各模塊耦合。

如圖12所示，根據IEC標準DLC 1.2工況定義[28]，選用平均風速15 m/s的湍流風，并利用TurbSim軟件生成時序風速。水動力計算采用白噪聲波譜，有效波高為1.264 6 m。仿真時間步長設為0.012 5 s，仿真時間為200 s。圖13～18所示為分別采用帶寬整定和BP神經網絡整定的變槳距LADRC與PID控制之間的對比分析。

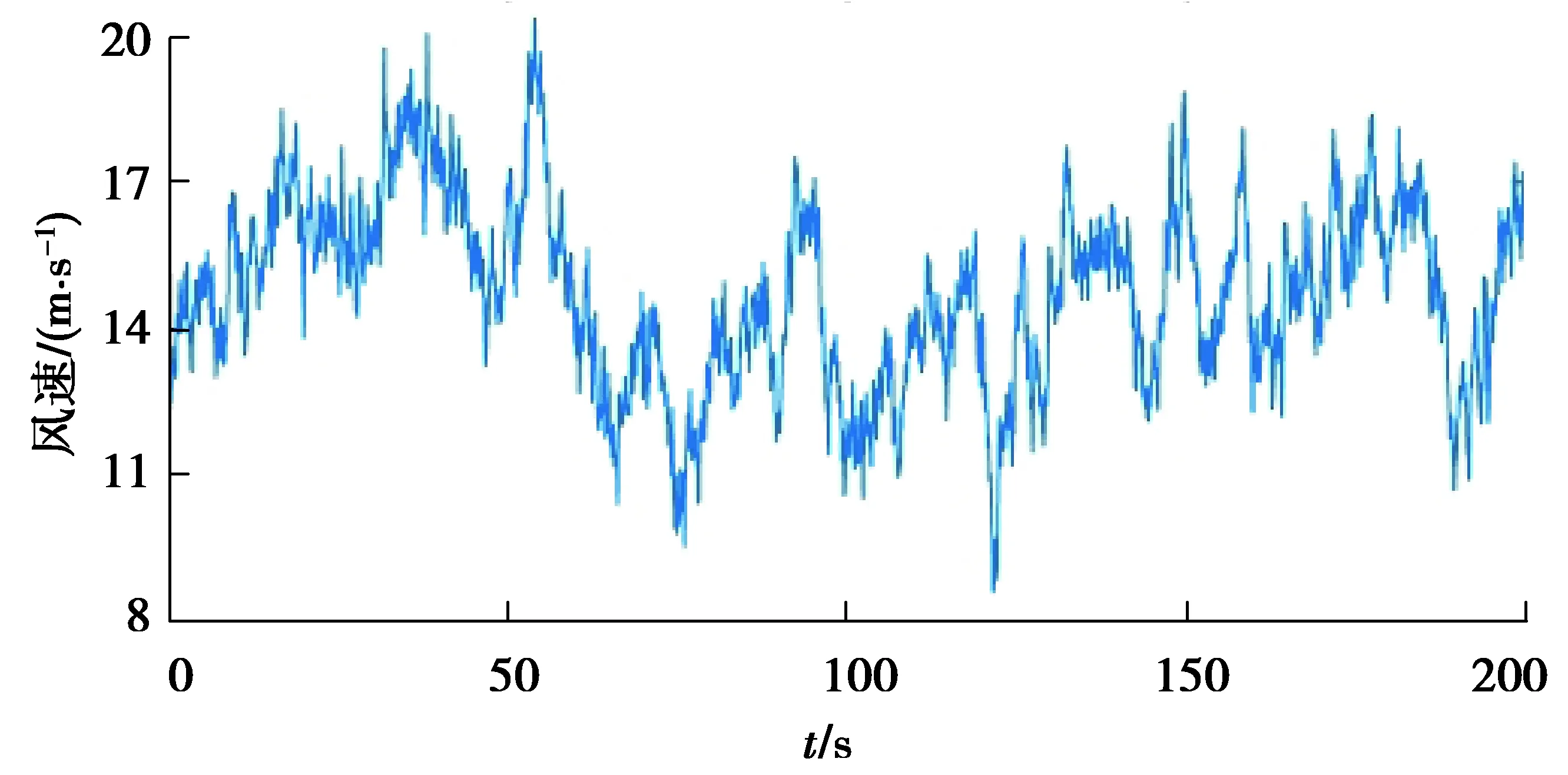
圖12 時序隨機風速Fig. 12 Time series random wind speed

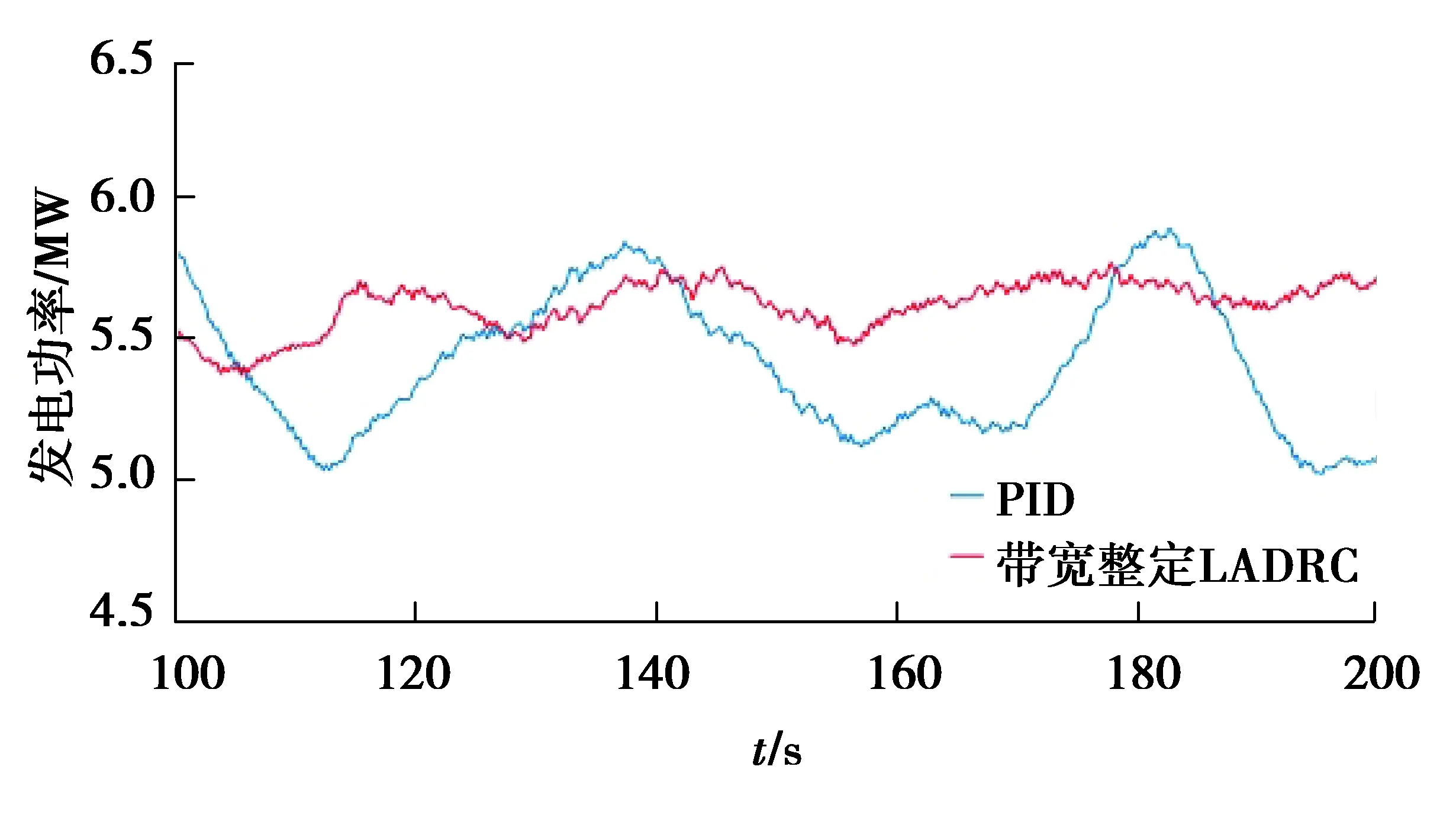
圖13 PID控制和帶寬整定LADRC下發電功率對比Fig. 13 Comparison of generator power between PID control and bandwidth tuning LADRC

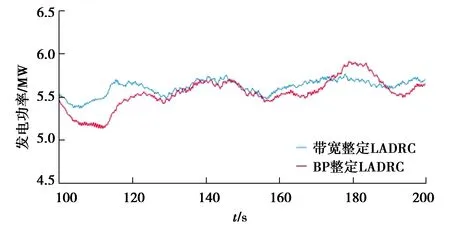
圖14 帶寬整定和BP神經網絡整定LADRC發電功率對比Fig. 14 Comparison of generator power between bandwidth setting and BP neural network

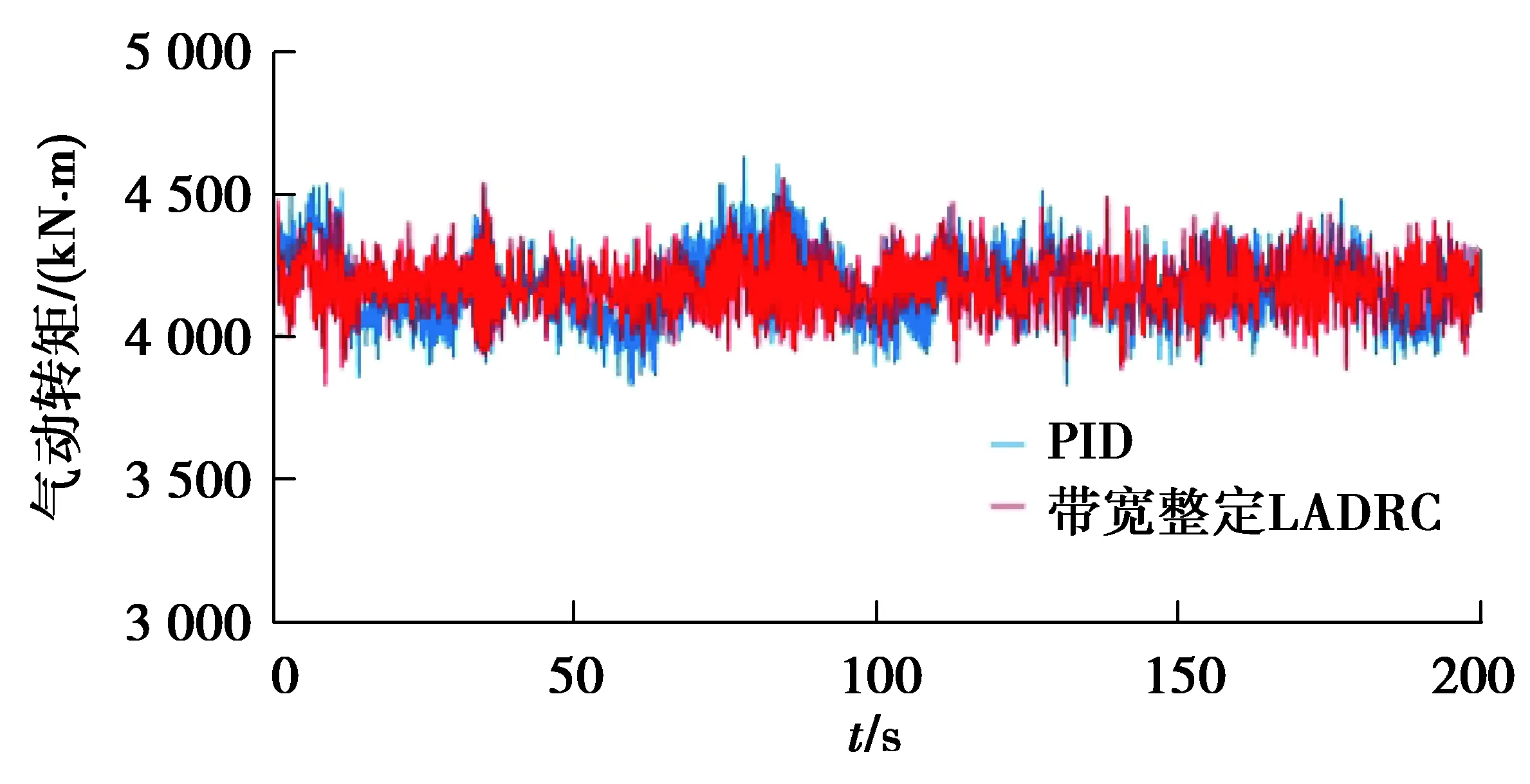
圖15 PID控制和帶寬整定LADRC下氣動轉矩對比Fig. 15 Comparison of aerodynamic torque between PID control and bandwidth tuning LADRC

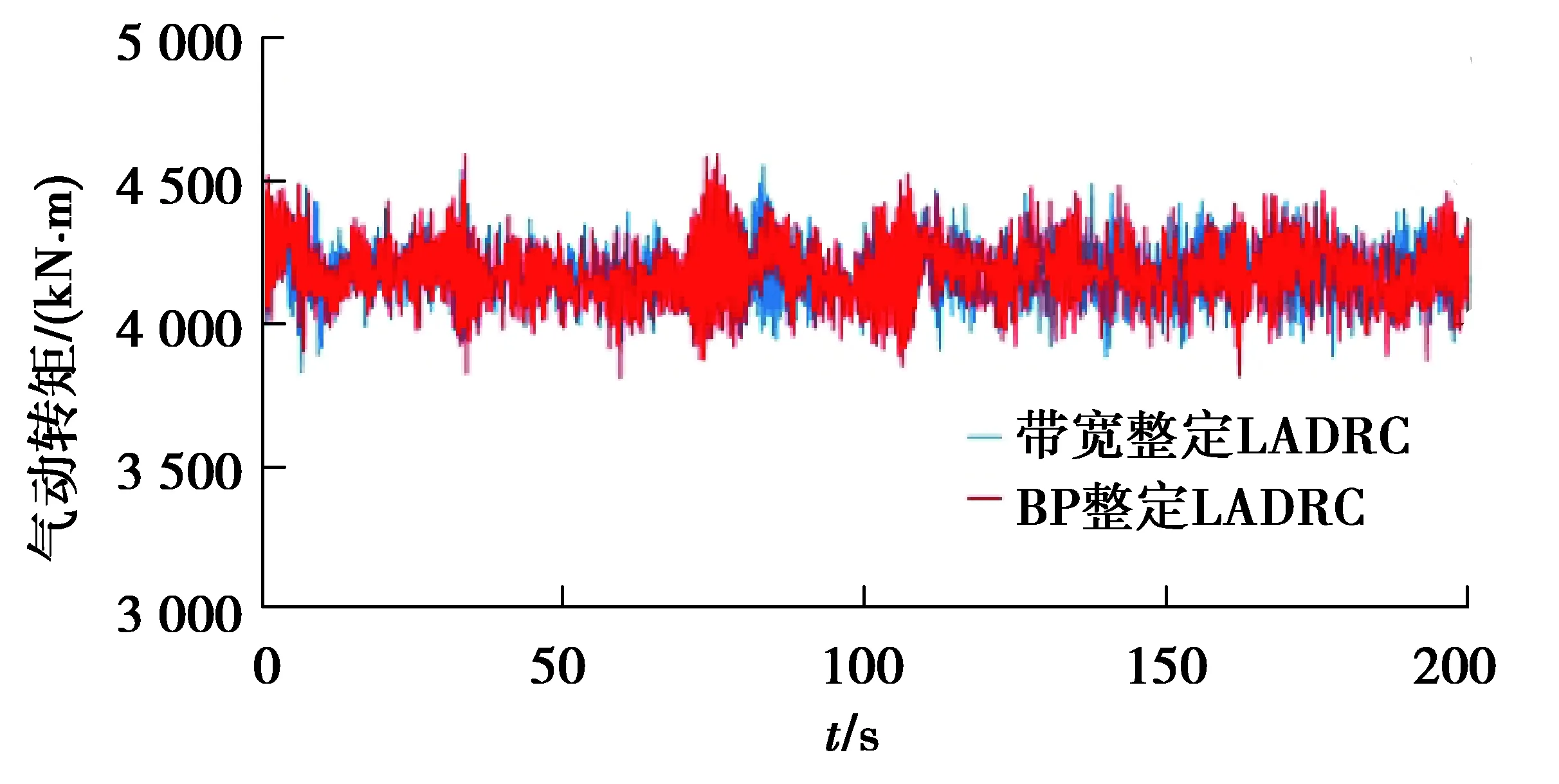
圖16 帶寬整定和BP神經網絡整定LADRC氣動轉矩對比Fig. 16 Comparison of aerodynamic torque between bandwidth tuning and BP neural network tuning LADRC

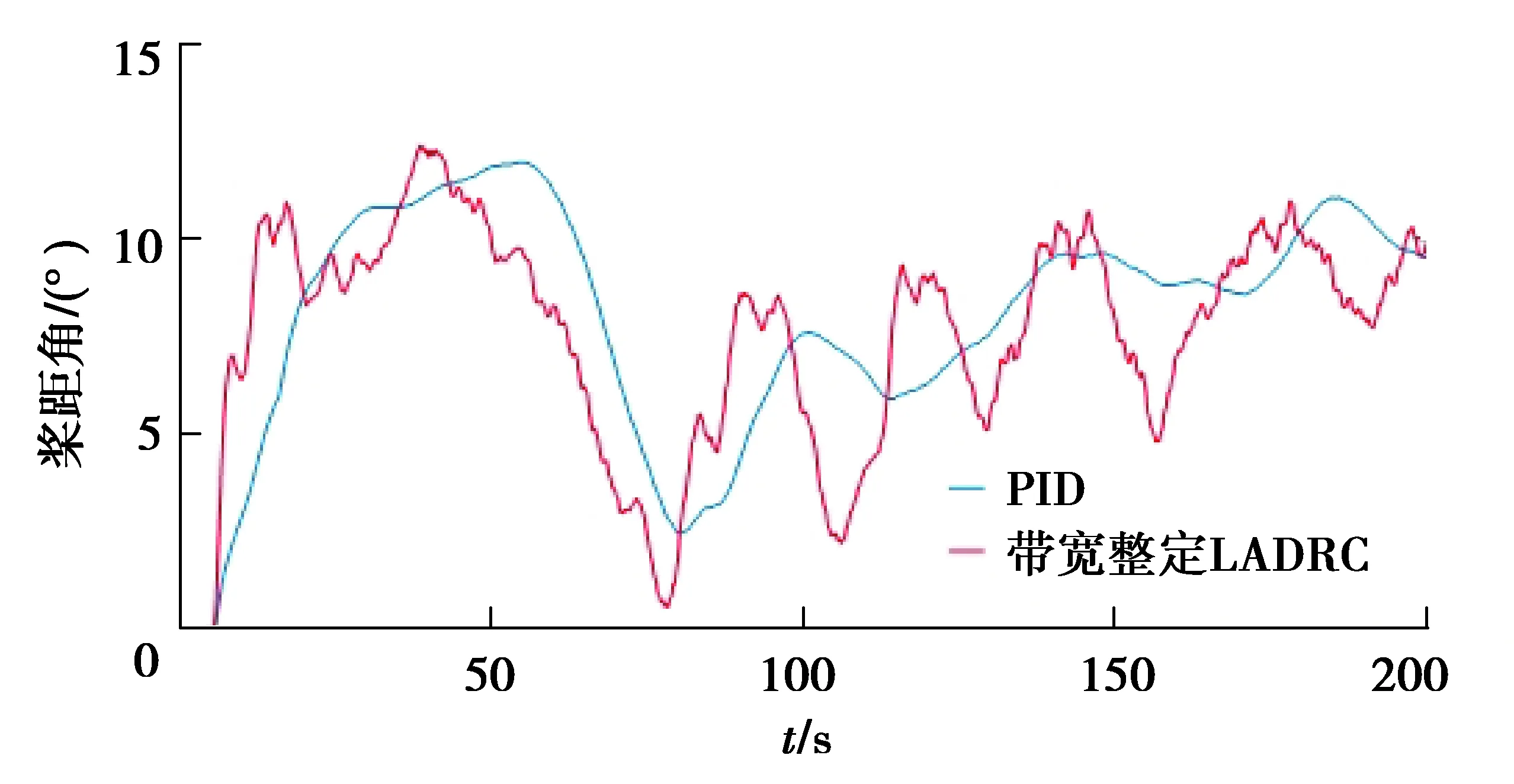
圖17 PID控制和帶寬整定LADRC下槳距角對比Fig. 17 Comparison of pitch angle between PID control and bandwidth tuning LADRC

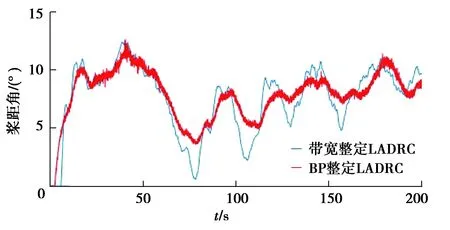
圖18 帶寬整定和BP神經網絡整定LADRC下槳距角對比Fig. 18 Comparison of pitch angle between bandwidth setting and BP neural network

圖13和圖14為風電機組穩定運行狀態下100～200 s的發電功率。對比圖13和14可以看出，LADRC和PID都可以穩定發電功率在5 MW附近，但相對于PID，變槳距LADRC的發電功率曲線標準差減少了約30%。

對比圖17和18的槳距角可以看出，針對風速變化，LADRC控制下的槳距角能迅速做出反應，而PID控制的槳距角反應略慢。對比兩種參數整定方法可以看出，BP神經網絡整定LADRC控制下的槳距角波動幅值小于帶寬整定。

此外，根據IEC標準DLC 1.2工況定義，選用3種相同湍流強度NTM B，對比不同平均風速下發電功率，如圖19所示。

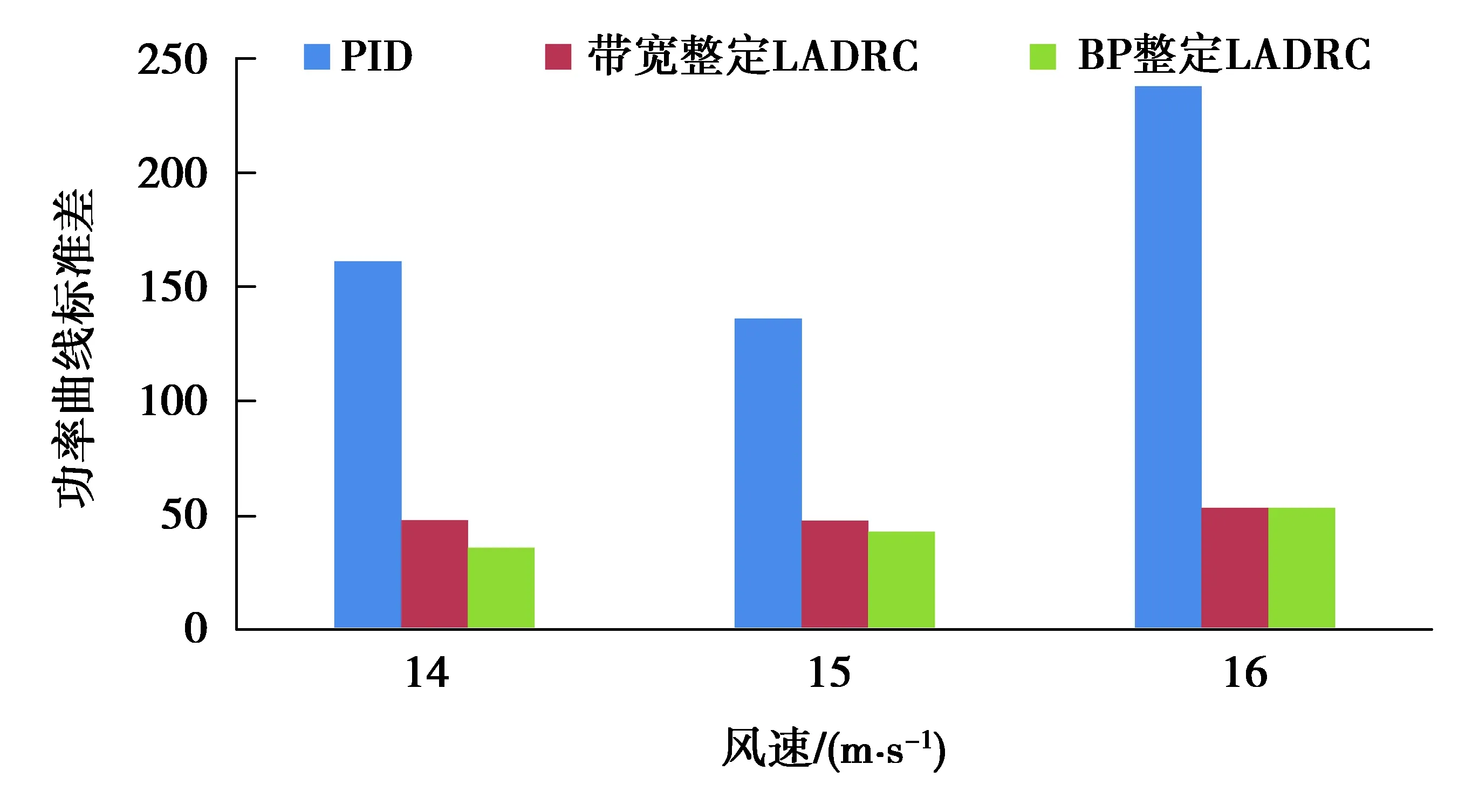
圖19 不同風速的功率曲線標準差對比Fig. 19 Comparison of standard deviations of power curves of different wind speeds

從圖19中可以看出，LADRC控制下的發電功率波動情況明顯小于PID。當平均風速為14 m/s時，相比傳統PID控制，采用LADRC的發電功率曲線標準差減少了約60%。在不同平均風速下，采用LADRC的發電功率波動均顯著小于PID，而基于BP神經網絡整定LADRC的發電功率波動幅值與帶寬整定整體相近。由此可得，變槳距LADRC控制器在不同風速條件下均有較好的控制效果。

5 結 論

1)在隨機風、浪載荷聯合激勵下，海上浮式風電機組發電功率將發生大幅波動，傳統PID變槳距控制無法有效進行抑制。

2)所設計的變槳距線性自抗擾控制器可以快速地將海上浮式風電機組發電功率穩定在額定值附近，相比傳統PID變槳距控制可有效減少發電功率波動。

3)提出利用BP神經網絡對變槳距線性自抗擾控制器進行參數整定，整定后的控制器對發電功率波動抑制的性能與帶寬整定相近，且適應不同風速。