基于擺線滾輪陰模基體的步長伸縮雙圓弧插補算法
肖 向,黃 健,陳佳豪,陳兵奎
(重慶大學 機械傳動國家重點實驗室,重慶 400044)
擺線針輪行星傳動具有傳動比大、傳動精度高、結構緊湊、扭轉剛度高和傳動效率高等突出優點,被廣泛應用于工業機器人、化工、冶金等領域[1-3]。擺線齒廓的精度是影響其傳動精度的主要因素,采用金剛石滾輪修整技術的成形磨削法不僅加工效率和精度高,而且可實現擺線齒廓的任意修形,已經成為擺線齒廓精加工的主流方法[4-5]。
高精度復雜形面金剛石滾輪一般采用內電鍍法制造[6],滾輪陰模基體形面是金剛石顆粒的定位基準面,其形面精度是影響滾輪最終制造精度的關鍵因素[7-8]。金屬陰模基體在數控精密磨床上加工,對于擺線金剛石滾輪陰模基體的數控磨削加工,由于基體形面曲線復雜,必須用直線或圓弧段逼近原曲線[9],為了提高其數控加工精度,插補算法的研究至關重要。
張敬東等[10]提出了一種等誤差直線插補算法用于擺線齒廓的數控加工;姚必強等[11]提出用等弧長圓弧擬合任意非圓曲線;CAD/CAM方法也廣泛應用于復雜非圓曲線的數控加工,該方法的刀具路徑由許多細小的直線或圓弧段組成[12-13]。用上述方法擬合復雜非圓曲線,當需要較高的插補精度時,插補節點數量多,且刀具路徑不具備G1連續性。采用雙圓弧插補法能有效解決上述問題,劉濤等[14-15]采用最優切向量雙圓弧插補算法完成渦旋型線零件的數控加工,但該方法需要根據曲線能量極小條件計算最優切向量,計算量大,擬合效率較低。
筆者基于雙圓弧插補法,求解出擺線滾輪陰模基體形面曲線方程,建立擺線滾輪陰模基體步長伸縮雙圓弧插補數學模型,利用MATLAB軟件求解插補節點數據,并進行誤差分析,通過控制步長伸縮來調整插補誤差。最后通過計算實例驗證了該模型的可行性,在相同允差要求下可以提高加工效率,插補數據擬合的加工仿真曲線光滑平整,刀具路徑具備G1連續性,插補節點數據導入數控機床即可用于數控程序編制。
1 擺線滾輪陰模基體形面曲線方程
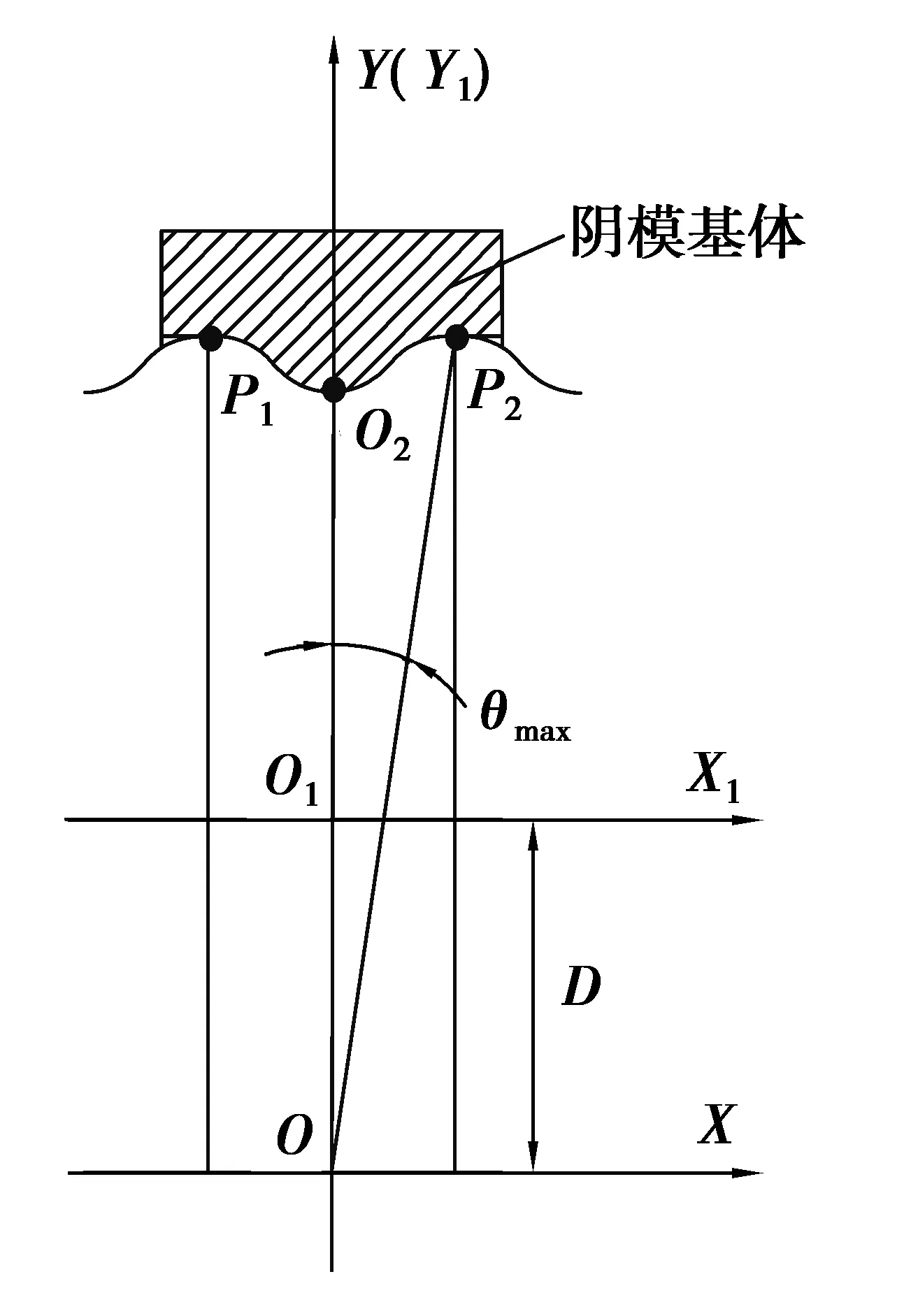
圖1 擺線滾輪陰模基 體加工坐標系Fig. 1 Machining coordinate system of female mold workpiece
擺線滾輪陰模基體加工坐標系如圖1所示,陰模基體加工坐標系為O1-X1Y1,擺線齒廓坐標系為O-XY,O1X1軸線與OX軸線的距離為D。擺線滾輪陰模基體形面曲線除P1O2P2段外皆為過渡圓弧及直線段,P1O2P2段曲線與擺線齒廓曲線形狀相同,且P1O2段曲線與O2P2段曲線關于Y1軸左右對稱,因此只需對陰模基體形面O2P2段曲線進行雙圓弧插補計算。
O2P2段形面曲線在擺線齒廓坐標系中的曲線方程式為:
(1)
式中:Rz為針輪中心圓半徑;e為偏心距;zb為針輪齒數;zg為擺線輪齒數;rz為針齒半徑;ΔRz為移距修形量;Δrz為等距修形量;K=ezb/(Rz+ΔRz);θ∈[0,θmax];θmax=π/zg。
對O2P2段形面曲線在擺線齒廓坐標系中的曲線方程式進行雙圓弧插補計算后,通過簡單的平移變換矩陣即可將插補節點數據轉換到陰模基體加工坐標系中,再將數據導入數控機床便可完成數控加工程序的編制。
2 擺線滾輪陰模基體步長伸縮雙圓弧插補數學模型
2.1 雙圓弧插補原理
圖2為雙圓弧插補原理圖,在加工曲線上任取相鄰2點ti(xi,yi)、ti+1(xi+1,yi+1),Ti、Ti+1分別為曲線上點ti、ti+1的切矢,過ti、ti+12點沿切矢方向作兩線段相交于點T得到△titi+1T,△titi+1T的內心是圖2中的M點。
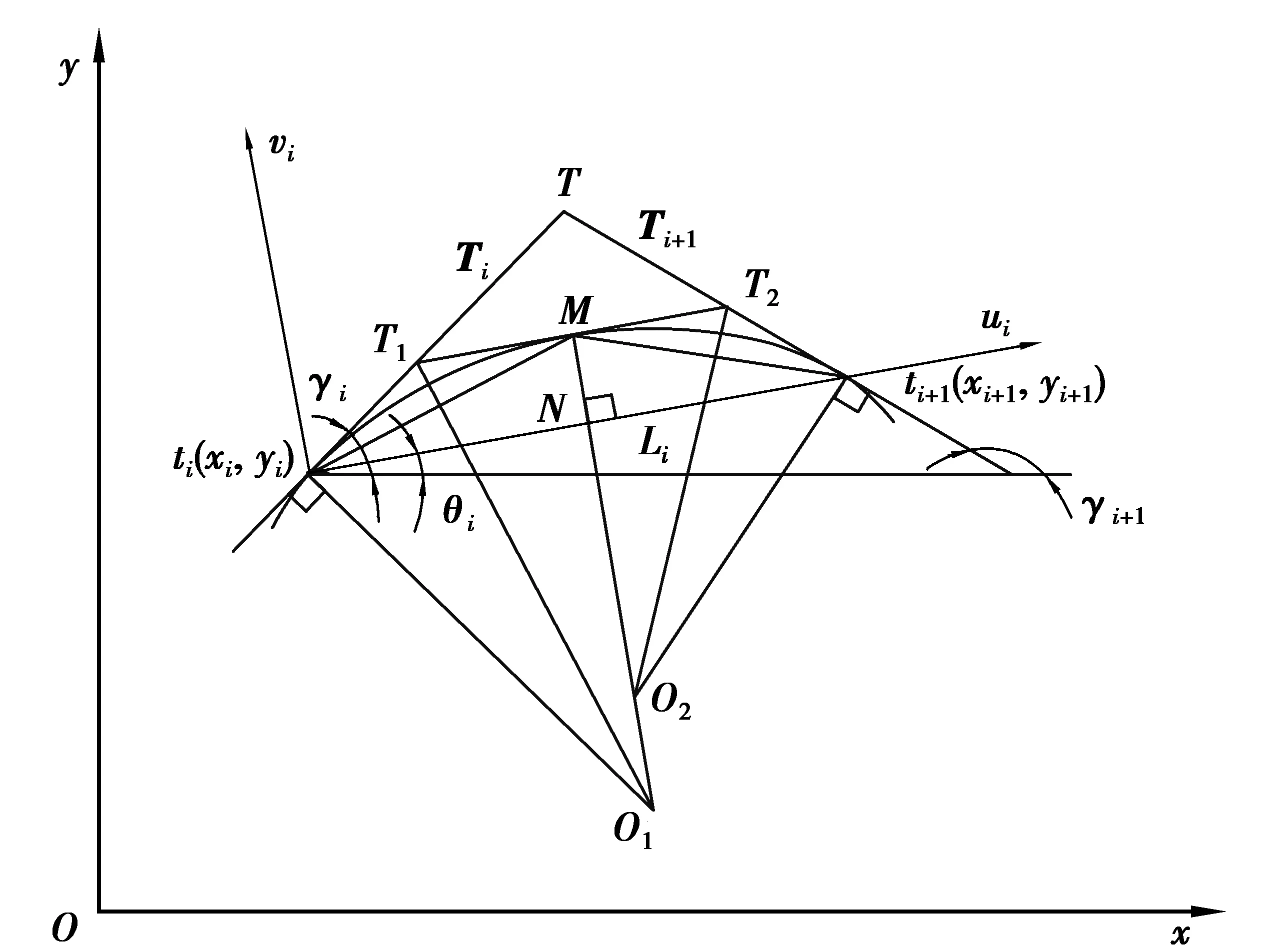
圖2 雙圓弧插補原理Fig. 2 Principle of double arc interpolation
過ti、ti+1點分別作線段tiT、ti+1T的垂線,同時過M點作線段titi+1的垂線與上述2條垂線交于O1、O2點。以O1點為圓心,O1ti為半徑作圓弧,圓弧起點為ti,終點為M;同理以O2為圓心、O2ti+1為半徑確定另一段起點為ti+1、終點為M的圓弧,由此確定了復雜曲線上任意相鄰2點間的插補雙圓弧段[16]。
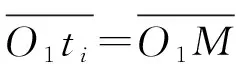
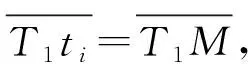
當完成ti與ti+12點間雙圓弧插補計算后,繼續進行下一相鄰2節點ti+1、ti+2間的計算,Ti+1、Ti+2分別為原加工曲線上點ti+1、ti+2的切矢,設ti+1與ti+22點間插補圓弧段對應的圓心分別為O3、O4。由以上雙圓弧插補原理分析可知,圓心O2對應的圓弧與切矢Ti+1相切于ti+1點,圓心O3對應的圓弧同樣與切矢Ti+1相切于ti+1點,故不僅相鄰節點ti、ti+1間插補的雙圓弧段具有公共切向量,而且同一節點ti+1兩側的圓弧段在節點ti+1處也具有公共切向量Ti+1。因此當采用雙圓弧法插補擺線滾輪陰模基體形面曲線時,插補的圓弧段在任意連接點處均有公共切向量,刀具路徑具有G1連續性。
2.2 雙圓弧半徑及公切點坐標參數計算
在圖2中,設整體坐標系為o-xy,o-xy是固定坐標系;局部坐標系為ti-uivi,ti-uivi是動坐標系。在o-xy坐標系中,設線段tiT、ti+1T與x軸的夾角為γi、γi+1,線段titi+1與x軸的夾角為θi,線段titi+1的弦長為Li。
γi及γi+1的值可以通過切矢Ti、Ti+1求得,由陰模基體形面曲線方程式(1)可求得Ti、Ti+1,故有
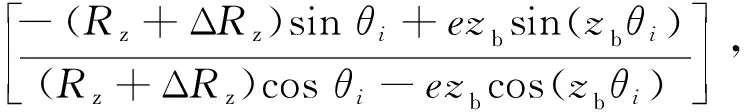
(2)
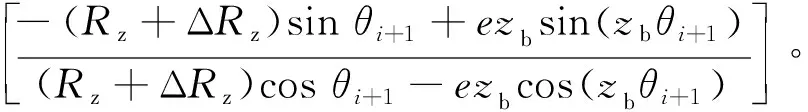
(3)
線段titi+1與x軸的夾角為
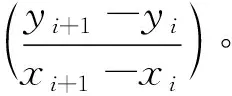
(4)
線段titi+1的弦長為
(5)
設點M在坐標系o-xy、ti-uivi中的坐標矢量分別為(xM,yM,1)T、(uM,vM,1)T,局部坐標系到整體坐標系的變換矩陣為M0i,可求得
(6)
局部坐標系中的坐標矢量可通過變換矩陣M0i轉換到整體坐標系中
(xM,yM,1)T=M0i(uM,vM,1)T。
(7)
如圖3所示,局部坐標系ti-uivi中,由內心幾何性質可知,Mti平分∠Ttiti+1(圖中β1),Mti+1平分∠Tti+1ti(圖中β2)。
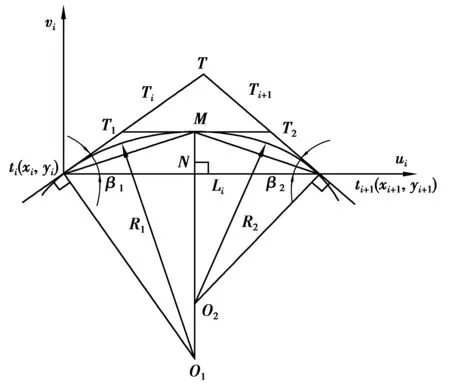
圖3 雙圓弧坐標計算Fig. 3 Double arc coordinate calculation
在△titi+1T中,內角β1、β2為
β1=γi-θi,
(8)
β2=π-(γi+1-θi)。
(9)
在△titi+1M中,由正弦定理可以推出
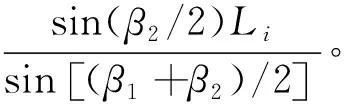
(10)
由于∠MNti、∠TtiO1均為90°,可以求出
ltiN=ltiMcos(β1/2),
(11)
lMN=ltiMsin(β1/2),
(12)
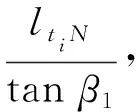
(13)

(14)
因此在局部坐標系下,可以求出公切點M坐標為
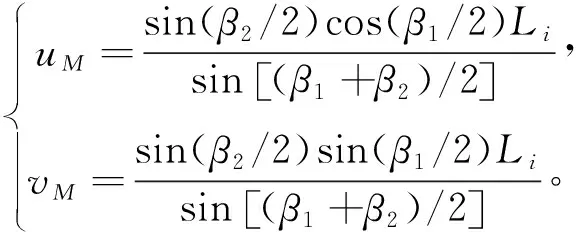
(15)
圓心O1、O2坐標分別為
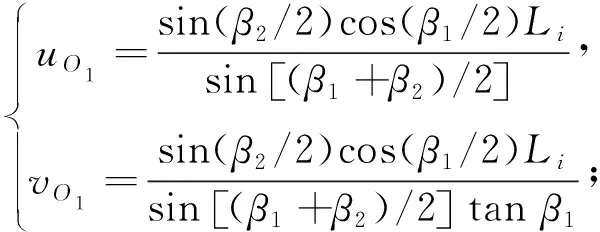
(16)
(17)
兩段圓弧半徑R1、R2為
(18)
圓弧半徑值R1、R2和公切點M及圓心O1、O2在局部坐標系中的坐標值均已計算完畢,通過坐標變換矩陣M0i即可得到公切點M及圓心O1、O2在整體坐標系中的坐標值。
2.3 擺線滾輪陰模基體雙圓弧插補誤差分析
完成兩個節點間的插補計算后,需要對產生的插補誤差進行分析控制。插補誤差的理論值是原廓形曲線上任意點沿其法線方向上與插補圓弧曲線間距離的最大值,在實際應用中可簡化計算,取原廓形曲線上任意一點到插補圓弧圓心的距離與兩段圓弧半徑(R1或R2)之差的最大值為插補誤差。
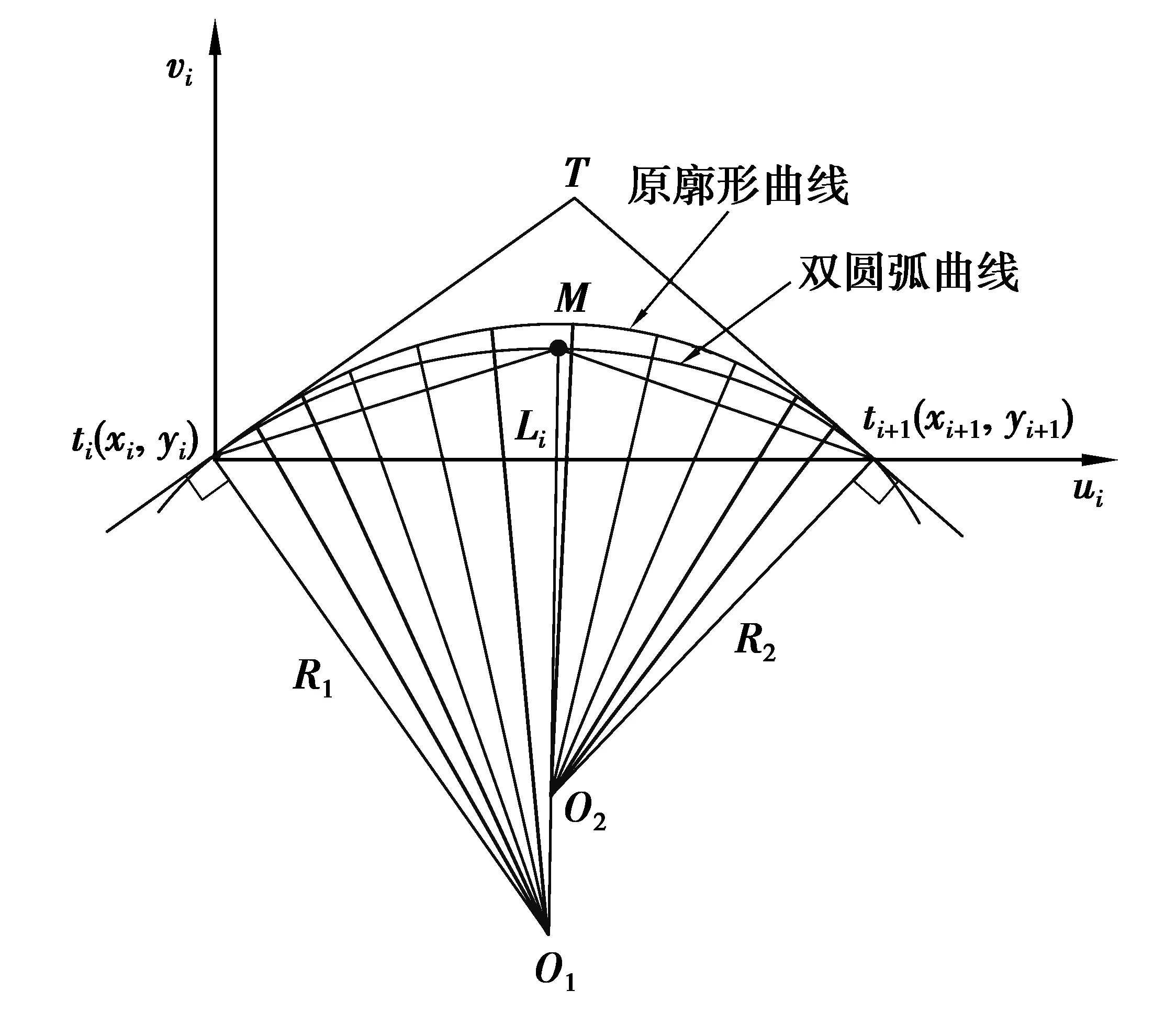
圖4 插補誤差計算Fig. 4 Calculation of interpolation error
上圖中Li為兩節點ti、ti+1之間的直線距離,將Li等分為N+1段,一般N+1取10到15,將等分點的橫坐標轉換到整體坐標系中求出擺線滾輪陰模基體形面曲線上的點pj(xj,yj)(j=1,2,…,N),比較xj與xM(圓弧公切點橫坐標值)的大小,當xj≤xM時,原形面曲線被擬合成第一段圓弧,此時的插補誤差為
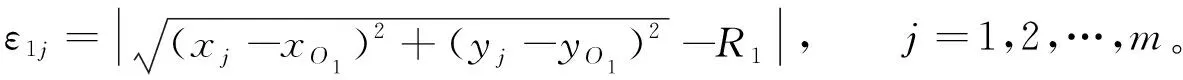
(19)
式中m是第一段圓弧對應的最后一個等分點,且m 當xj>xM時,原形面曲線被擬合成第二段圓弧,此時的插補誤差為 (20) ε1j與ε2j中的最大值即為這兩個節點間的插補誤差ε,即 ε=max(ε1j,ε2j)。 (21) 判斷任意相鄰兩節點間的插補誤差ε與所允許的插補誤差σε的大小,如果ε>σε,縮小步長直至滿足ε<σε的要求;而當ε遠小于σε時,可適當增大步長使得插補誤差小于并接近于插補允差,這就是步長伸縮雙圓弧插補算法的實質。 進行雙圓弧插補時,如果插補段曲線凹凸性不一致,會出現S型擬合圓弧。因此曲線上若存在拐點應將曲線分段再進行插值計算。曲率計算公式為 (22) 由曲率k=0求得O2P2段曲線拐點處參數角為 (23) 因此O2P2段曲線需分為[0,θ1]、[θ1,θmax]兩段進行雙圓弧插補計算。 O2P2段曲線的步長伸縮雙圓弧插補算法計算步驟如下: 1)給定初始參數角θ0和初始步長角Δ,計算相鄰2節點的坐標ti(xi,yi)和ti+1(xi+1,yi+1)及相應節點處的切矢Ti、Ti+1,由雙圓弧插補計算原理求出公切點M、圓心O1、O2點坐標值及相應圓心半徑R1、R2的值。 2)將相鄰2節點間的插補誤差與插補允差σε比較,同時為了提高加工效率,對插補允差設定一個下限值σεmin。若ε>σε,步長角減小一半調整曲線上節點ti+1的位置重新進行插補計算直至滿足誤差要求;若ε<σεmin,適當增大步長角使插補誤差接近插補允差,當θi≥θmax時,終止計算。 擺線滾輪陰模基體步長伸縮雙圓弧插補算法流程如圖5所示。 圖5 步長伸縮雙圓弧插補算法流程圖Fig. 5 Flow chart of variable-step-double-arc interpolation algorithm 取40E擺線輪工件參數作為計算實例參數,其中e=1.3,zb=40,zg=39,rz=2.5,Rz=63.7,ΔRz=-0.1,Δrz=0.075,θ∈[0,π/39]。將上述參數代入擺線滾輪陰模基體形面曲線方程式中,根據上節中的插補算法流程在MATLAB軟件中編程進行數值計算。 初始參數角θ0=0,初始步長角選取0.001 2 rad,插補允差σε=0.01 μm。以初始步長角等分參數角取相同插補節點數,可以得到69個插補節點。分別采用雙圓弧插補法與直線插補法對O2P2段曲線進行插補計算,在O2P2段曲線上隨機連續選取8個插補節點,插補誤差對比結果如表1所示。 表1 雙圓弧與直線插補誤差對比結果 當節點數目相同時,表中結果顯示直線插補只有最后2個節點之間的插補誤差小于插補允差,其他節點間的誤差遠大于插補允差σε,而雙圓弧插補誤差均小于插補允差σε。直線插補最小誤差為0.009 μm,雙圓弧插補最大誤差為2.176 nm,雙圓弧插補最大誤差比直線插補最小誤差降低了75%,對比任意節點處得到的數據發現插補誤差均降低75%以上。 等步長角得到的雙圓弧插補誤差曲線如圖6(a)所示,通過分析插補節點的坐標可知,在超過一定參數角后,繼續以滿足插補誤差的步長角插補時,會導致插補節點過于集中,從而插補誤差的最值出現數量級的差距,加工程序更加冗長,且加工零件表面質量不均勻。 采用圖5所示的步長伸縮雙圓弧插補算法,對加工允許誤差設定一個下限值σεmin=0.001 μm,當插補節點間的誤差小于下限值時,適當增加步長角調整節點ti+1在曲線上的位置,使得插補誤差小于并接近插補允差。 圖6(b)是控制步長角伸縮后的插補誤差曲線圖,插補誤差均小于插補允差σε。在滿足同一插補允差時,等步長角的插補節點數為69個,控制步長角伸縮后插補節點數為30個,節點數目減少了55%,插補的圓弧段也減少了55%。因此在相同插補允差要求下控制步長角伸縮可以提高擺線滾輪陰模基體工件的加工效率,同時可以保證加工表面質量均勻。 圖6 等步長角與伸縮步長角誤差曲線對比圖Fig. 6 Comparison of interpolation error curves of equal step angle and telescopic step angle 圖7曲線是由步長伸縮雙圓弧插補節點數據擬合的O2P2段加工仿真曲線,由于擬合的圓弧段在每個離散點處都有公共切向量,因此擬合曲線一階導數連續,擬合曲線表面光滑平整,刀具路徑具有G1連續性,保證了工件的加工質量。 圖7 O2P2段曲線加工仿真圖Fig. 7 Processing simulation diagram of O2P2 curve 以擺線金剛石滾輪陰模基體為加工對象,基于雙圓弧插補法,建立了擺線滾輪陰模基體步長伸縮雙圓弧插補數學模型,該模型插補點求解方便,控制步長伸縮可以調整插補誤差。對該數學模型進行實例計算及仿真,得出結論如下: 1)雙圓弧插補誤差小于0.01 μm,在節點數相同時其插補誤差比直線插補誤差降低75%,滿足擺線滾輪陰模基體高精度加工要求。 2)控制步長伸縮,在同精度允差下擬合圓弧段數減少55%,可以提高擺線滾輪陰模基體工件的加工效率。 3)由插補算法原理及插補數據擬合的加工仿真曲線可知,插補的任意相鄰圓弧段彼此相切,擬合曲線表面光滑連續,刀具路徑具備G1連續性。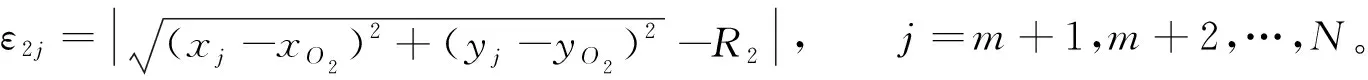
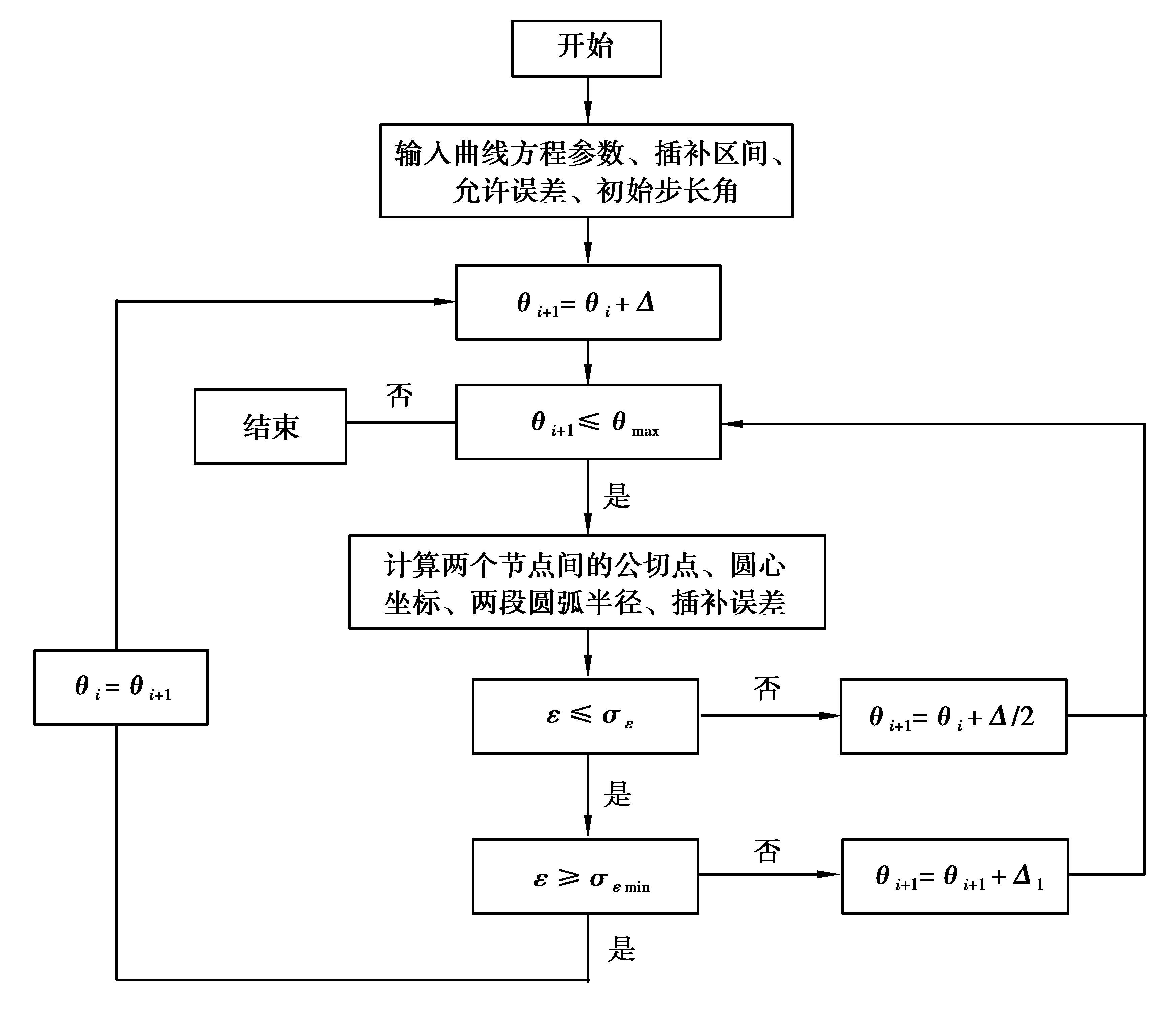
2.4 擺線滾輪陰模基體步長伸縮雙圓弧插補算法
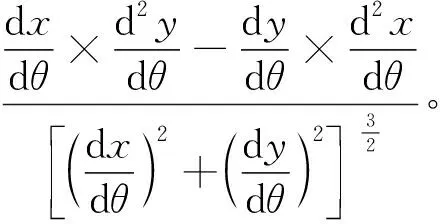

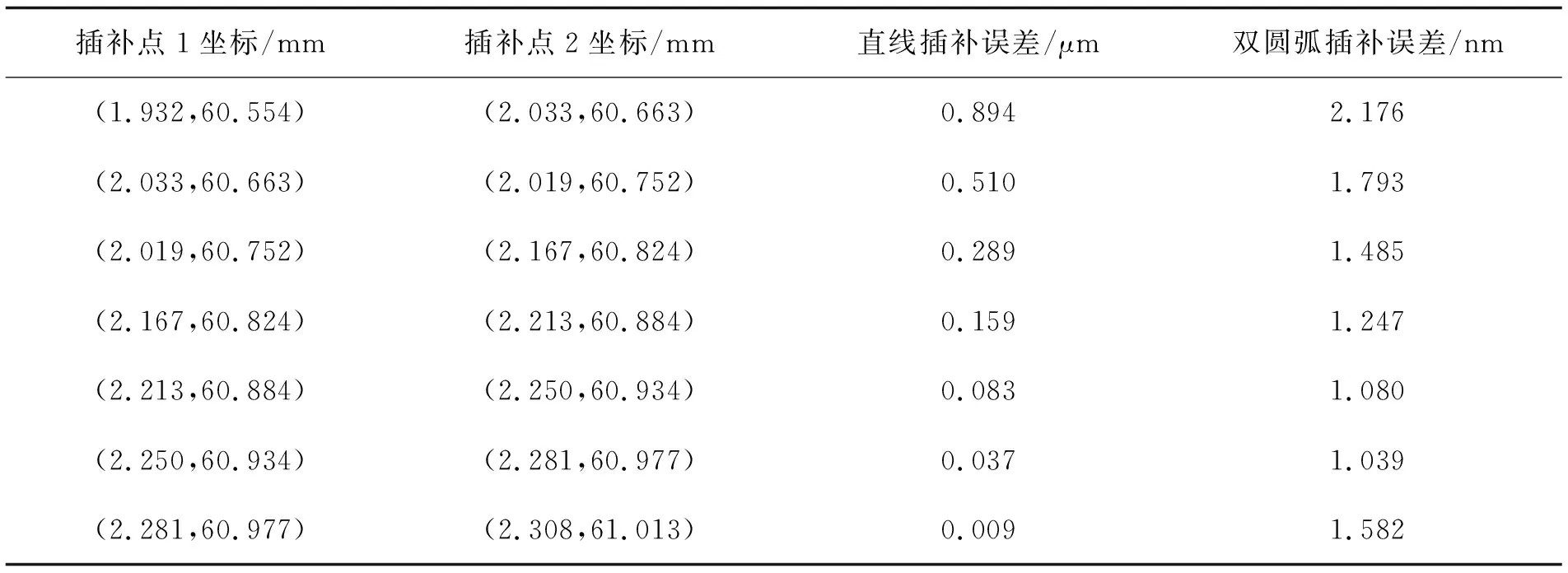
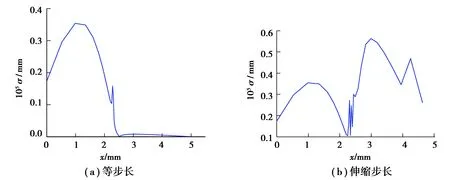
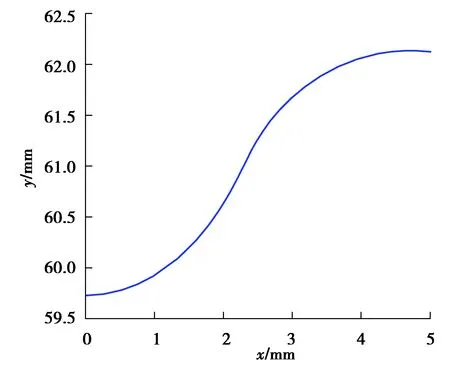
3 計算實例分析及仿真
4 結 論

