前后獨立驅動電動汽車轉矩分配與驅動防滑協調控制
郭 聰,傅春耘,1b,翟 鈞,曹開斌,羅榮華,劉 洋,潘宏偉,喬帥鵬
(1. 重慶大學 a. 機械與運載工程學院;b.機械傳動國家重點實驗室, 重慶 400044; 2. 重慶長安汽車股份有限公司, 重慶 400023)
隨著純電動汽車相關技術的快速發展,分布式驅動電動汽車已成為現階段的研究熱點。最典型的分布式驅動構型之一為輪轂電機驅動,此類驅動形式省去了大量傳動部件,傳動效率較高[1]。與傳統集中式驅動相比,該構型可對各輪的驅動轉矩進行獨立控制,更容易實現直接橫擺力偶矩控制、驅動防滑控制等功能[2-4]。然而,這種構型的控制算法更為復雜,對控制系統的實時性和精確性要求較高,且存在輪轂電機安裝空間受限、簧下質量增大等問題[5]。另一類分布式驅動形式是前后獨立驅動,該構型可看作是介于集中式驅動與輪轂電機驅動之間的一種過渡形式。該構型中,兩個電機分別安裝在前后驅動橋上,仍保留了主減速器、差速器和半軸等傳動部件,可實現前后橋驅動轉矩獨立控制。與輪轂電機驅動相比,雖不能實現左右輪間的轉矩分配,但車輛的橫向穩定性得到充分保證[6-7],并且具有較高的可靠性[8]。這種驅動形式目前已被各大廠商廣泛采用,代表車型如特斯拉Model Y、蔚來ES8等。因此,本文中選擇前后獨立驅動四驅電動汽車作為研究對象。
針對前后獨立驅動電動汽車的轉矩分配問題,已有學者提出了不同的控制方法。Yuan等[9]研究了前后獨立驅動電動汽車的能耗優化問題,他們通過分析電機及傳動部件的功率損耗發現,與單電機驅動的情況相比,將總轉矩均勻分配給兩個電機可以提高車輛的經濟性,但該方法只適用于兩個電機特性相同的情況。Fujimoto等[10]設計了一種針對前后獨立驅動四驅電動汽車的轉矩分配控制策略,轉矩分配比的范圍設定為[0,1.5],該值超過1表示后軸用于驅動,前軸進行再生制動回收能量。仿真結果表明,在循環工況下,所提出的控制策略提高了車輛的續駛里程。此外,多軸獨立驅動構型的轉矩分配問題也有類似的解決方案。喬帥鵬等[11]以多軸輪邊電機驅動卡車作為研究對象,提出了一種適用于多軸驅動車輛的驅動力優化分配策略,由于該策略沒有考慮車輛的橫向運動,同一軸上的兩臺輪邊電機始終輸出相同的轉矩,所以該策略同樣適用于多軸獨立驅動的結構。首先,根據電驅動系統效率最大化原則以及動態軸荷變化確定驅動軸數和具體驅動軸;其次,將整車需求轉矩均勻分配到各個驅動軸;最后,各驅動軸上的轉矩再均勻分配給左右輪邊電機。
在對電動汽車進行轉矩分配時,必須充分考慮路面的附著條件,防止驅動輪因無法輸出目標轉矩而發生打滑,即在進行轉矩分配時必須同時引入驅動防滑控制,防止因車輪打滑而產生車輛失穩等危險情況。范晶晶等[12]提出了多軸獨立電驅動車輛的驅動力分層協調控制方法,上層分別以動力性、經濟性和通過性為目標設計轉矩分配策略,下層根據車輪滑移率調整前后軸驅動轉矩,最大限度地利用地面附著力。Tong等[13]基于滑模控制理論設計了一種電動汽車轉矩分配控制策略,首先遵循經濟性優先的原則,將總需求轉矩均分給兩個驅動軸;然后通過縮小前后輪滑移率差異的方法,限制驅動輪的滑移率,提高車輛的穩定性。He等[14]和Zhang等[15]分別提出了分布式驅動電動汽車牽引力集成控制策略,默認以經濟性為首要目標,當某一軸上驅動輪的滑移率超過允許值時,則減小該軸的驅動轉矩以控制車輪滑移率,同時將減去的部分補充到另一驅動軸上,以保證整車總驅動力不變。由現有文獻可知,傳統集成控制策略(traditional integrated control strategy, TICS)只是將基于經濟性的轉矩分配與驅動防滑控制進行簡單組合:即車輛默認以經濟性優先原則行駛,當某個軸的車輪滑移率超過最佳滑移率時,防滑控制系統介入,通過降低該軸的驅動轉矩使車輪滑移率趨近于最佳滑移率。此外,TICS僅考慮了車輛處于四驅模式的情況,沒有考慮不同驅動模式(前驅、后驅、四驅)對整車性能的影響,且在防滑控制系統介入后完全忽略了整車經濟性。
針對傳統集成控制策略存在的缺點,提出一種改進的轉矩分配與驅動防滑協調控制策略(coordinated control strategy, CCS)。首先,基于前后驅動電機的map圖,以效率最大化為準則,設計轉矩分配控制策略;基于滑模控制理論,設計驅動防滑控制策略。然后,設計驅動轉矩協調控制策略,引入可以表征前后電機控制模式的全局變量,通過分析車輪滑移率和全局變量的變化,以及電機總需求轉矩、滿足經濟性要求的前后電機轉矩、路面條件所允許的最大轉矩三者之間的關系,確定前后電機的控制模式和目標轉矩。最后,利用MATLAB/CarSim軟件進行仿真,驗證所提出的轉矩分配與驅動防滑協調控制策略的有效性。
1 整車建模
1.1 車輛縱向動力學模型
圖1為前后獨立驅動四驅電動汽車的驅動系統結構示意圖。該電動汽車的前后軸分別由兩個電機獨立驅動,每個電機輸出的動力經主減速器、差速器和半軸傳遞到驅動輪。前后電機的輸出轉矩由控制單元進行調節,從而實現前后軸驅動轉矩的合理分配。
(1)
式中:Treq為前后電機所發出的總驅動轉矩,N;i0為傳動系統減速比;ηt為傳動系統效率;r為車輪半徑,m;m為車輛整備質量,kg;g為重力加速度,m/s2;f為滾動阻力系數;ρ為空氣密度,kg/m3;Cd為空氣阻力系數;A為迎風面積,m2;v為車輛質心速度,km/h;δ為旋轉質量轉換系數;α為坡度角,(°)。
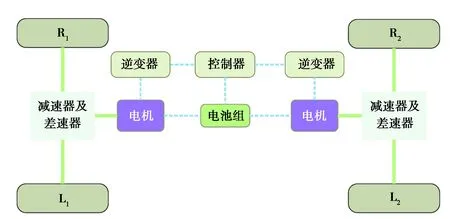
圖1 前后獨立驅動電動汽車驅動系統結構Fig. 1 Drive system structure of a front- and rear-independent-drive electric vehicle
圖2所示為電動汽車單個車輪的動力學模型。由牛頓運動定律和剛體轉動微分方程,可得如下動力學方程[17]:
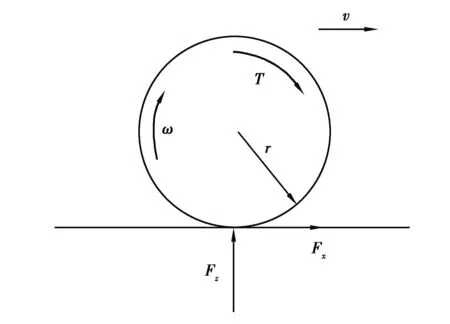
圖2 單個車輪的動力學模型Fig. 2 Dynamic model of single wheel
(2)
(3)

1.2 駕駛員模型
采用一個PID控制器來模擬駕駛員對車輛的加減速操作[18, 19]:PID控制器的輸入是目標車速和實際車速的誤差,PID控制器的輸出則是踏板的開度,即:
(4)
ev=vref-v;
(5)
eout=ysat-y;
(6)
(7)
式中:Kp為比例系數;Ki為積分系數;Kd為微分系數;Kaw為抗飽和系數;vref為目標車速,km/h;y表示踏板開度(加速為正,減速為負)。規定踏板開度在[-1,1]范圍內變化,并引入函數ysat作為y的限制邊界。
由于車輛需求轉矩與踏板開度成正相關,定義踏板開度與總需求轉矩的關系如下:
Treq=yTmax(nm)=y[Tmax_mf(nm)+Tmax_mr(nm)]。
(8)

1.3 電機模型
由于電機效率特性具有非線性的特點,難以利用函數或方程精確表達,現有研究通常采用實驗法獲取電機效率數據。本文中采用的前后電機參數見表1,其效率特性如圖3所示。
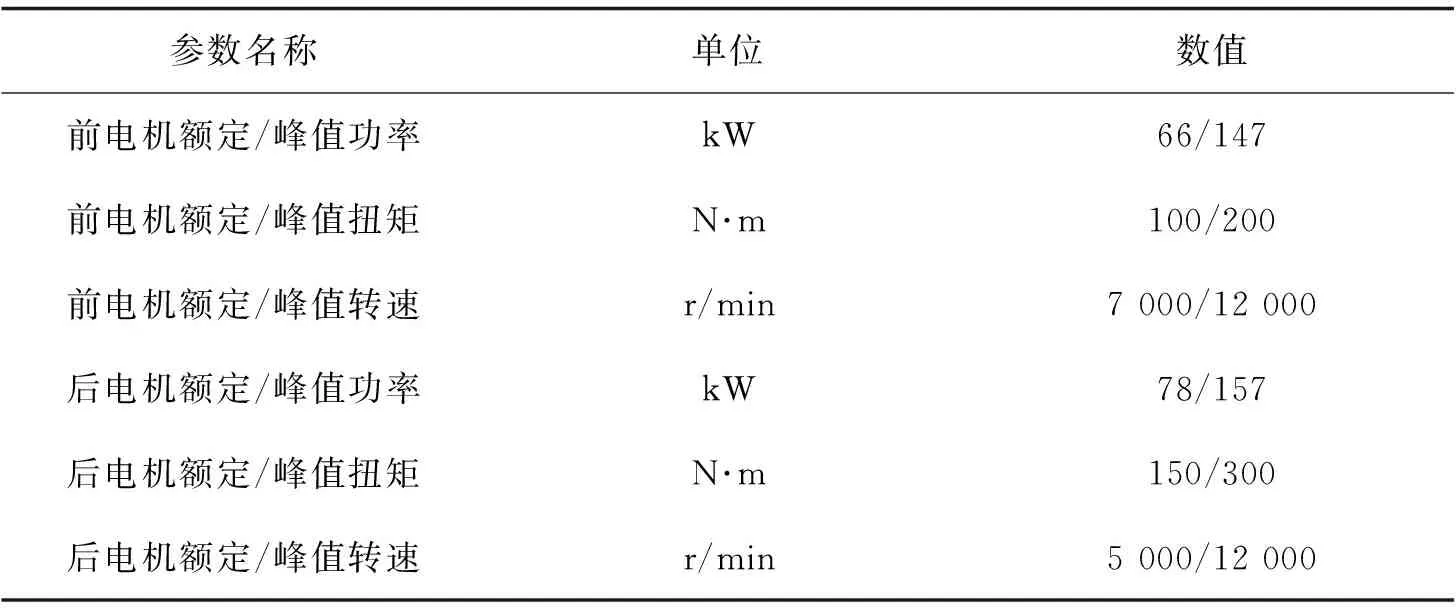
表1 前后電機參數
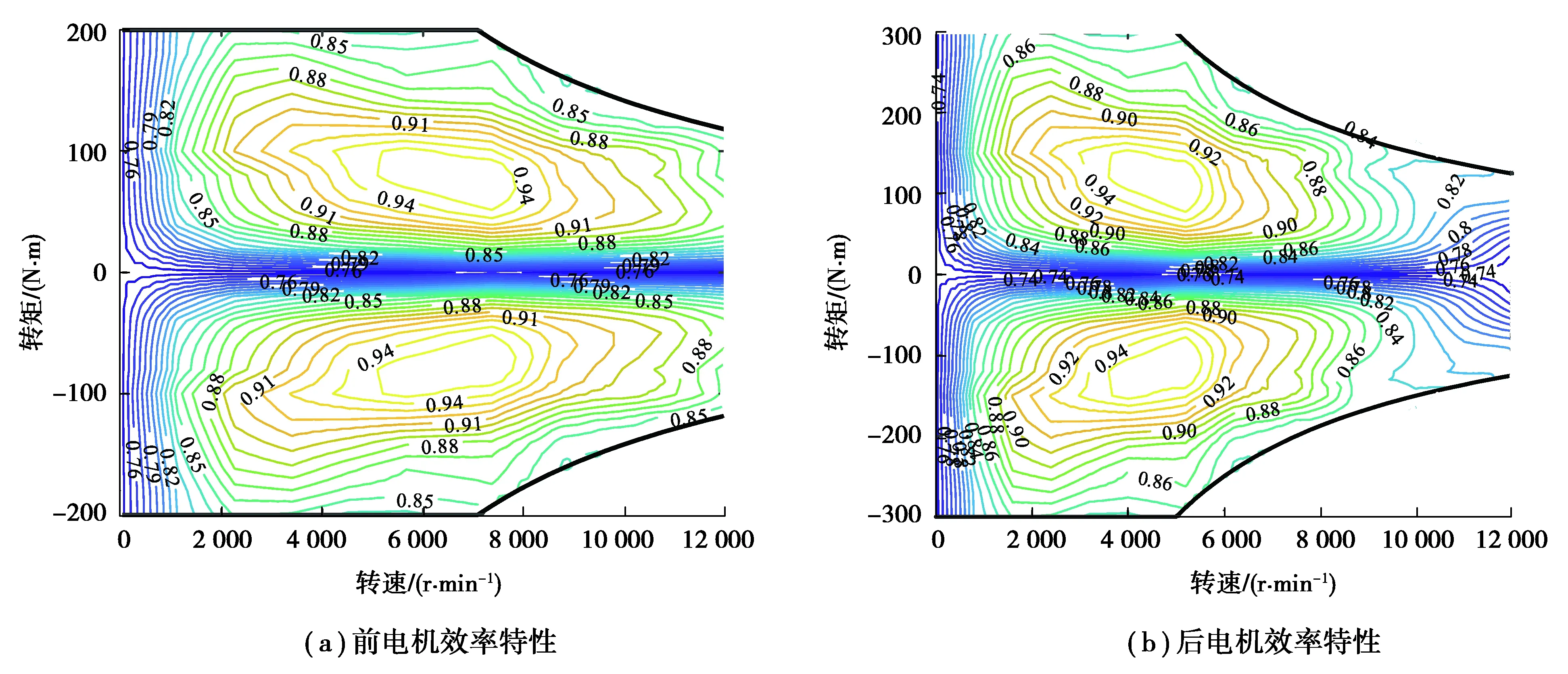
圖3 前后電機效率特性圖Fig. 3 Efficiency maps of the front and rear motors
在實際工作過程中,電機響應會有一定的延遲,所以采用慣性環節表示電機響應特性:
(9)

因電機、減速器、車輪之間通過齒輪嚙合傳遞動力,故電機的轉速與轉矩可用下列公式表示:
(10)
(11)
(12)
式中:nmj為電機轉速,r/min;Pmi為電機輸出功率,kW;Pmj_in為電機輸入功率,kW;ηmj(Tmj,nmj)為電機在相應轉矩和轉速下的工作效率。
1.4 電池模型
電池組的充放電特性受到環境溫度、充放電電流的影響[20]。由于電池組建模不是本研究的重點,因此在滿足控制器設計需求的前提下,采用如下簡化的電池組模型來描述電池特性[21]:
Pb=Pmf_in+Pmr_in=EI-I2R0,
(13)
(14)
(15)

2 控制器設計
2.1 基于經濟性最優的轉矩分配策略
對于前后獨立驅動的電動汽車,前后電機的輸出轉矩之和應滿足整車的動力需求,即:
Treq=Tmf+Tmr,
(16)
Tmf=kTreq,
(17)
Tmr=(1-k)Treq。
(18)

為提升電動汽車的經濟性,在滿足動力需求的前提下應使前后電機總需求功率盡可能小。由于電機在不同轉速和轉矩時的工作效率不同,所以可建立如下成本函數J用于整車能耗優化[22-24]:
(19)
(20)
式中:nmf、nmr分別為前后電機轉速,r/min;nmax_mf、nmax_mr分別為前后電機的峰值轉速,r/min。需要指明的是,制動工況涉及到電機再生制動,超出本文討論的范疇,本文中只針對驅動工況下的經濟性進行討論。
為了縮短控制策略的計算耗時,提高控制策略的實時性,本文中采用可行空間離散化求解的方法[23-26]:首先在離線條件下對滿足約束條件的所有工況點進行離散化處理,對每一個離散后的工況點尋找最佳的轉矩分配方案,即通過遍歷尋優求解滿足式(19)的最優轉矩分配比k,然后以表格的形式儲存該最優分配比。控制器工作時可根據實時工況直接查表取值,避免了進行大量的在線運算。根據式(19)求解出的全工況下轉矩分配比如圖4所示,可以看出:當車輛處于低速高轉矩工況時,采用后電機單獨驅動;當車輛處于高速低轉矩工況時,采用前電機單獨驅動;當車輛處于高速高轉矩或總需求轉矩超過單個電機峰值轉矩時,采用雙電機同時驅動。J取得最小值時,最佳轉矩分配結果由式(21)(22)表示:
Tmf_opt=koptTreq,
(21)
Tmr_opt=(1-kopt)Treq。
(22)

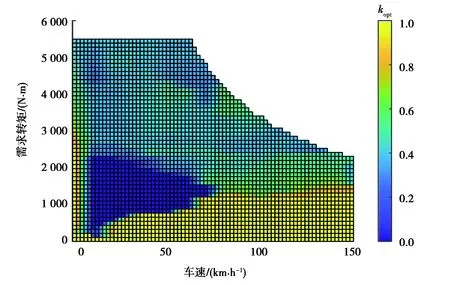
圖4 全工況下轉矩分配比Fig. 4 Torque distribution ratio under full working conditions
2.2 驅動防滑控制策略
在實際應用中,受車輛行駛阻力、車輪參數的不確定性的影響[27],控制算法不僅要能夠迅速響應,還應具有良好的抗干擾能力。鑒于滑模控制的高魯棒性,本文中采用滑模控制方法來處理車輪的滑移問題。本節詳細闡述基于滑模控制的驅動防滑控制策略的詳細設計過程,并分析控制系統的穩定性條件。
車輛在行駛過程中,車輪滑移率λ可定義為:
(23)
式中ω為車輪的角速度,rad/s。
實際滑移率與最佳滑移率的誤差e可表示為:
e=λ-λ0,
(24)
式中λ0為最佳滑移率。需要說明的是,在不同的路面附著條件下,λ0的值也不同。此外,在車輛實際運動控制中,車輪滑移率(車速)和路面附著系數難以通過傳感器直接獲取,已報道的研究中一般利用狀態觀測器對車輛的實際車速和路面附著系數進行在線估計[28-29]。由于狀態觀測器的設計不是本研究的重點,故本文不對此做詳細討論,并假設車輪滑移率與路面附著系數可準確獲取。
為了減小系統的穩態誤差,提高控制精度,可設計如下切換函數[30-31]:
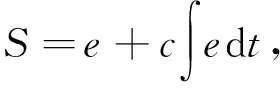
(25)
式中c為常數。
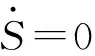
(26)
欲使系統狀態能夠到達滑模面,須引入如下監督控制量Ts[32]:
Ts=εsgn(S),
(27)
式中ε為控制增益。則滑模控制律為:
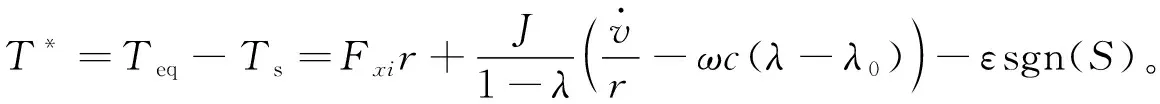
(28)
為保證切換函數S逐漸趨近于0并保持S= 0(即系統狀態保持在滑模面上),引入如下穩定性條件[33]:
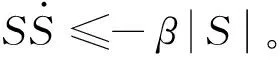
(29)
其中:
(30)
當S為正值時:
(31)
式中β為常數。
當S為負值時:
(32)
綜合式(31)和(32),最終可得如下穩定性條件:
(33)
式(27)所表示的監督控制量中的符號函數sgn(S)是不連續的,在實際應用中會引起系統的抖振。為了抑制系統抖振,采用飽和函數sat代替原符號函數,故最終的滑模控制律可表示為:
(34)
式中φ為邊界層厚度。
在本研究中,對前后電機獨立進行控制(即前后電機各有一個滑模控制器),當前(后)軸驅動防滑控制作用時,前(后)電機的期望輸出轉矩可表示為:
(35)
(36)
式中:λf0、λr0為前后輪的最佳滑移率;λf、λr為前后輪的實際滑移率;ωf、ωr為前后輪的角速度,rad/s;εf、εr為前后控制器的控制增益;Sf、Sr為前后控制器的切換函數;cf、cr為常數。
2.3 協調控制策略
上文2.1節和2.2節中設計的轉矩分配控制器與驅動防滑控制器分別以提升經濟性和保證安全性為控制目標。然而在實際應用中,由于兩種控制器的控制作用可能相互沖突,因此不能直接將兩者的功能進行簡單組合。必須結合路面條件和車輛的行駛工況對兩種控制器的控制作用進行有效協調,從而使控制系統的綜合性能最優。
本文中提出的協調控制策略如圖5和6所示,在該控制策略中定義了2個全局變量Mode_f和Mode_r來表示前后電機的控制模式。首先,基于2.1節中提出的轉矩分配控制器和2.2節中提出的驅動防滑控制器,分別得到滿足經濟性要求和安全性要求的前后電機轉矩。然后,通過本節提出的協調控制策略決策出前后軸的最佳驅動轉矩,提高電動汽車的綜合性能。
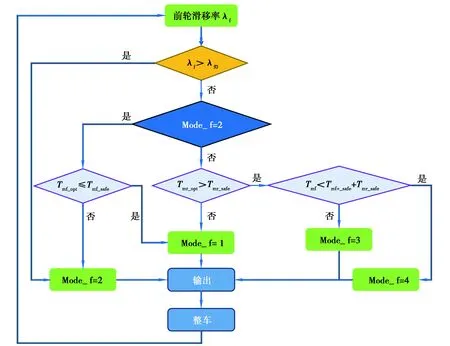
圖5 前電機協調控制策略Fig. 5 Coordinated control strategy for front motor
全局變量Mode_f,r的取值及對應的含義如下:
1)Mode_f,r= 1。該模式下,以經濟性最優確定電機輸出轉矩,即電機的輸出轉矩為:
Tmf=Tmf_opt,Tmr=Tmr_opt。
(37)
2)Mode_f,r= 2。該模式下,因路面附著條件的限制,前后軸能夠提供的驅動力受路面附著條件的約束。為了使車輪實際滑移率能夠收斂于最佳滑移率,電機的輸出轉矩為:
Tmf=Tmf_safe,Tmr=Tmr_safe。
(38)
3)Mode_f,r= 3。當Tmf_opt、Tmr_opt差異較大或車輛處于單軸驅動狀態,且前后輪均處于低附著系數的路面時,使驅動轉矩較小的軸增加補償轉矩來提高整車的動力性。此時該軸電機的輸出轉矩為:
Tmf=Tmf_opt+ΔT,Tmr=Tmr_opt+ΔT;
(39)
且有:
(40)
式中有ΔT為補償轉矩。
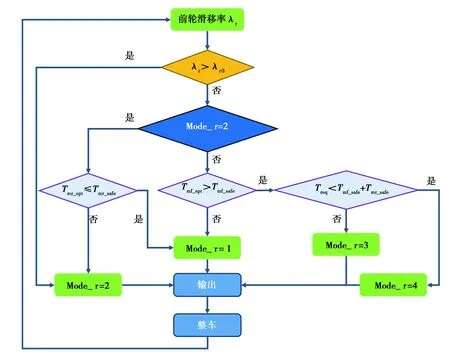
圖6 后電機協調控制策略Fig. 6 Coordinated control strategy for rear motor
4)Mode_f,r= 4。該模式下,優先保證車輛的動力性。當前后輪處于對接路面時,為滿足駕駛員的動力需求,利用處于良好路面的軸來補償總驅動轉矩的不足,盡可能保證整車的動力性不受影響。此時該軸電機的輸出轉矩為:
Tmf=Treq-Tmr_safe,Tmr=Treq-Tmf_safe。
(41)
因為對前后電機的控制是獨立的,所以分別針對前后軸的控制策略進行討論。對前軸而言,電機控制模式的判斷邏輯如下:
1)判斷前輪實際滑移率是否超過當前工況的最佳滑移率。若為是,說明當前路面附著條件不足以提供車輛所需驅動力,為防止前輪滑移率過大,控制器將輸出Mode_f= 2以降低前電機轉矩,保證車輛安全性;若為否,則有如下2種可能的情況:
a.前輪出現打滑后,在防滑控制器的作用下,車輪實際滑移率收斂于最佳滑移率;
b.當前路面附著條件足以提供經濟性行駛所需的驅動力,車輪未發生打滑。
2)檢查全局變量Mode_f的值,若Mode_f= 2,則表明發生上述a種情況;若Mode_f≠ 2,則表明發生b種情況。若a發生,由于基于經濟性最優的轉矩分配結果會隨車速發生變化,所以應進一步判斷Tmf_opt≤Tmf_safe是否成立。若為是,則車輛重新遵循經濟性優先的原則,輸出Mode_f=1;若為否,則控制系統繼續優先保持安全性,輸出Mode_f= 2。若b發生,說明當前前輪滑移率較小,需進一步判斷是否對前軸施加補償轉矩,進入下一步。
3)判斷后電機是否滿足Tmr_opt>Tmr_safe,若為否,表明后輪所處的路面條件足以提供經濟性行駛所需的驅動力,則前電機保持控制模式不變,即輸出Mode_f=1;若為是,則可以確定后輪不能繼續維持經濟性目標,需要降低驅動轉矩以防止車輛失穩。同時,前軸需進行轉矩補償,進入下一步。
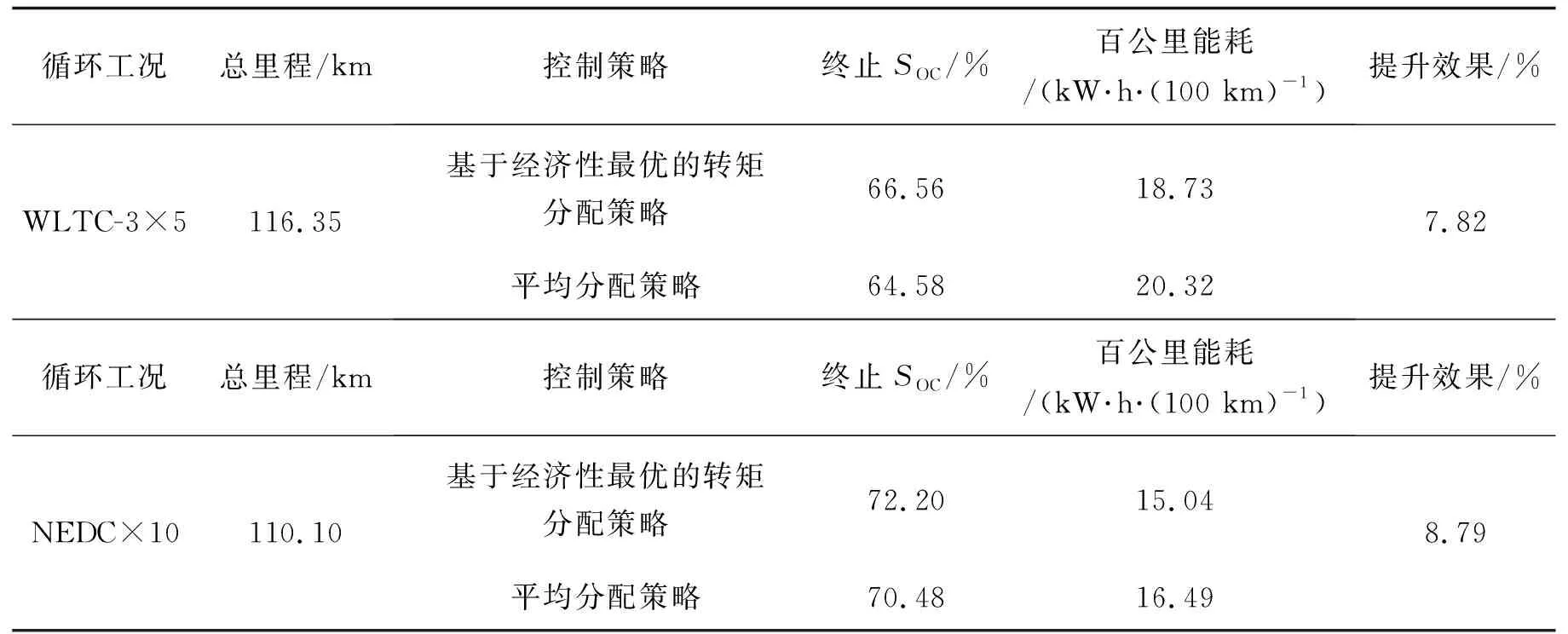
4)判斷是否存在Treq 后軸電機控制模式的判斷邏輯與前軸相似,不同之處在于,當路面條件較好時(全局變量Mode_r≠ 2),應判斷前電機轉矩是否滿足Tmf_opt>Tmf_safe以確定是否對后軸施加補償轉矩。若為否,則認為前輪所處的路面條件足以提供經濟性行駛所需的驅動力,輸出Mode_r=1;若為是,說明前輪驅動力受到路面附著條件的限制,前電機不能輸出經濟性最優轉矩,所以后電機應進行轉矩補償。 本研究基于MATLAB/CarSim聯合仿真平臺,首先針對第2節中設計的基于經濟性最優的轉矩分配策略和驅動防滑控制策略進行仿真試驗,以驗證上述兩種策略各自獨立作用時的有效性;然后設置不同工況,在同等條件下對本文中提出的CCS和現有的TICS進行對比仿真驗證。 本文中所提出的協調控制策略是以經濟性為基礎的,基于經濟性最優的轉矩分配策略的有效性對協調控制的最終性能具有重要影響。選擇WLTC-3和NEDC兩種典型循環工況來驗證轉矩分配策略的效果。由于單個循環工況的行駛里程較短,分別使用5個WLTC-3循環和10個NEDC循環進行仿真,并與轉矩平均分配策略進行對比。 電池SOC的仿真結果如圖7所示,在WLTC-3工況和NEDC工況下,與轉矩平均分配策略相比,采用基于經濟性最優的轉矩分配策略使電池SOC降低速度明顯減緩。表2展示了兩種工況下采用不同轉矩分配策略的能耗數據,可以看出基于經濟性最優的轉矩分配策略可以顯著降低車輛的百公里能耗,在WLTC-3工況下,經濟性提高了7.82%;在NEDC工況下,經濟性提高了8.79%。 圖7 兩種循環工況的SOC仿真結果Fig. 7 Simulated SOC under two types of drive cycles 表2 兩種循環工況的經濟性仿真結果 有無驅動防滑控制的車輪滑移率對比如圖8(a)所示。當沒有驅動防滑控制時,前后輪的滑移率在1 s后迅速上升至1附近,表明車輪已經發生嚴重打滑;相比之下,當驅動防滑控制介入時,在實際滑移率超過最佳滑移率后,驅動防滑控制器在0.2 s內使滑移率穩定在最佳值附近。圖8(b)展示了仿真過程中的轉矩變化,當滑移率超過最佳值時,驅動防滑控制器立即介入,限制前后電機的轉矩輸出,使滑移率收斂于最佳值。 圖8 加速工況的車輪滑移率與電機轉矩仿真結果Fig. 8 Slip ratios and motor torques under acceleration simulation 本文中提出的轉矩分配與驅動防滑協調控制策略旨在使車輛能夠應對復雜多變的路面狀況并發揮出最佳的性能。為全面驗證該策略的實用性、有效性,設置路面附著系數隨行駛距離變化,具體附著系數值見表3[15]。由于輪胎具有非線性特性,車輛行駛在附著系數不同的路面時,車輪的最佳滑移率隨路面條件差異而發生變化。為使車輛能夠最大程度利用路面附著條件,在CarSim中進行了輪胎測試,在特定的路面條件下,通過調整電機發出的轉矩來改變驅動輪的滑移率,并記錄不同滑移率對應的驅動力與垂直載荷數據,然后計算驅動力與垂直載荷的比值,該比值取得最大值時,對應的滑移率即為當前路面附著條件下的最佳滑移率。通過上述方法,獲得不同路面附著系數所對應的最佳滑移率,具體數值如表4所示。需要說明的是,當車輪恰好處于最佳滑移率時,輪胎可獲得最大縱向力,此時路面附著條件被充分利用;當實際滑移率小于最佳滑移率時,輪胎工作在線性區,是一種較安全的工況。因此,實際應用中一般允許車輪實際滑移率小于最佳滑移率。 表3 路面狀況 表4 不同路面的最佳滑移率 根據全工況下基于經濟性最優獲得的最優轉矩分配結果,車輛的驅動形式可能會在前驅、后驅和四驅之間切換。因此使用駕駛員模型,在不同的加速踏板開度下驗證所提出的協調控制策略(CCS)的控制效果,并與傳統集成控制策略(TICS)進行對比。 3.3.1 加速踏板開度為10% 圖9 10%加速踏板開度下的仿真結果Fig. 9 Simulation results with 10% accelerator pedal opening 圖9中的虛線為使用TICS得到的仿真結果。仿真開始時,車輛在路面附著系數為0.8的路面上行駛,此時以經濟性最優的原則行駛,前后電機控制模式均為1,且車輛為后電機單獨驅動;當t> 3.8 s時,后輪由良好路面進入附著系數為0.1的路面,后輪滑移率突然增大,此時控制器檢測到后輪滑移率超過最佳值,后電機控制模式立即切換為2。之后,汽車先后駛入附著系數為0.2和0.9的路面,因加速踏板開度較小,可繼續按照經濟性最優的原則行駛。 圖9中的實線為使用本文中提出的CCS得到的仿真結果。當后輪開始打滑時,防滑控制器介入使后電機轉矩減小以保持滑移率在最佳值附近,同時前電機施加轉矩補償。由于總需求轉矩較小,前電機可以補償足夠的轉矩以滿足駕駛員的動力需求,所以后電機控制模式切換為4。當t= 7.2 s時,雖然車輛仍處于附著系數為0.1的路面,但因最佳轉矩分配比的改變可以滿足車輛以經濟性最優行駛,所以此時前后電機的控制模式均切換為1。因路面條件的限制,前輪滑移率超過最佳值時,控制器將前電機控制模式切換為2,同時將后電機控制模式切換為4。當t= 9.5 s時,汽車前輪進入附著系數為0.2的路面,此時的最佳轉矩分配結果為前電機單獨驅動,控制器判斷認為當前路面條件可以滿足經濟性行駛所需轉矩,前后電機控制模式均切換為1,并且在汽車回到良好路面后仍然保持不變。在整個仿真過程中,CCS使前后輪滑移率均保持在最佳滑移率以下,并且總驅動轉矩時刻滿足駕駛員的動力需求。圖9(d)展示了車輛在兩種控制策略下的速度差異,CCS和TICS控制下汽車的末速度分別為42.9 km/h和37.2 km/h,即CCS對動力性能的提升效果達到15.3%。 3.3.2 加速踏板開度為30% 圖10 30%加速踏板開度下的仿真結果Fig. 10 Simulation results with 30% accelerator pedal opening 同樣地,車輛在良好路面行駛時,遵循經濟性優先原則,車輛由后電機單獨驅動。對于TICS,當t= 3.75 s時,汽車后輪駛入附著系數為0.1的路面,后輪滑移率迅速上升并超過當前路面條件對應的最佳滑移率,于是防滑控制器介入使滑移率穩定在最佳值附近,此時后電機控制模式為2。當t= 8.80 s時,汽車后輪駛入附著系數為0.2的路面,后電機轉矩增大以跟隨最佳滑移率,前電機控制模式不變。當t= 11.90 s時,汽車后輪駛入附著系數為0.9的良好路面,前后電機控制模式均為1。 CCS使車輛表現出更好的動力性,當后輪由良好路面駛入附著系數為0.1的路面后,后電機控制模式切換為2,同時前電機控制模式切換為3以施加轉矩補償,從而最大程度地利用路面條件。當t= 7.97 s時,汽車前輪先由附著系數為0.1的路面駛入附著系數為0.2的路面,在前輪滑移率不超過最佳值的前提下,前電機補償轉矩進一步增加;t= 8.24 s時后輪駛入附著系數為0.2的路面,后電機轉矩增加以跟蹤最佳滑移率。當t= 10.40 s時,汽車前輪駛入附著系數為0.9的路面,為滿足駕駛員對整車的動力需求,前電機控制模式切換為4,當后輪緊接著駛入良好路面后,前后電機控制模式均切換為1,汽車遵循能耗最優的原則行駛。仿真結束時,兩種策略下的汽車速度差異如圖10(d)所示,在CCS和TICS控制下汽車末速度分別為83.0 km/h和61.0 km/h,即CCS對動力性能的提升效果達到35.6%。 3.3.3 加速踏板開度為50% 圖11 50%加速踏板開度下的仿真結果Fig. 11 Simulation results with 50% accelerator pedal opening 由圖11(b)可知,仿真開始時,車輛行駛在良好路面,以經濟性優先的原則行駛,前后電機控制模式均為1。當t= 2.4 s時,汽車前輪先駛入低附著系數路面,前輪滑移率突然增大。在CCS作用下,前電機控制模式切換為2,后電機控制模式切換為4,直到后輪進入低附著系數路面后,后電機控制模式也切換為2。當行駛距離達到50 m時汽車前后輪依次駛入附著系數為0.2的路面,前后電機轉矩相應增大以跟蹤最佳滑移率;當t= 8.6 s時,汽車前輪駛入附著系數為0.9的良好路面,前電機控制模式切換為4以滿足駕駛員的動力需求;當t> 8.6 s時,所有車輪都進入良好路面后,路面條件足夠提供車輛經濟性行駛所需的前后軸驅動力,前后電機控制模式均切換為1。在仿真結束時,CCS與TICS使車輛的末速度分別為71.8 km/h和68.7 km/h,即CCS對于動力性能的提升效果達到4.5%。 針對前后軸獨立驅動的四驅電動汽車,提出了一種改進的轉矩分配與驅動防滑協調控制策略。一方面,該策略能夠使車輛適應復雜的路面條件,在良好路面上,車輛默認以經濟性最優行駛;當路面條件不能滿足經濟性最優行駛時,在保證車輪滑移率不超過最佳滑移率的前提下,通過轉矩補償盡可能改善車輛的動力性。另一方面,在該策略中設置兩個全局變量來表征前后電機的控制模式,根據實時的最優轉矩分配比以及滿足安全性要求的前后電機轉矩與總需求轉矩之間的關系,確定最佳輸出轉矩,實現了在車輛處于低附著系數路面且加速踏板保持不變的情況下,仍可恢復到經濟性模式行駛。仿真結果表明,在變附著系數路面上,當加速踏板開度分別為10%、30%、50%時,所提出的CCS使汽車末速度分別達到42.9 km/h、83.0 km/h、71.8 km/h。相比之下,TICS在相同加速踏板開度下,汽車的末速度分別為37.2 km/h、61.0 km/h、68.7 km/h,即本研究中提出的CCS使車輛的動力性能分別提升15.3%、35.6%、4.5%。3 仿真結果
3.1 轉矩分配策略(經濟性)驗證

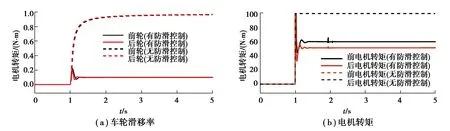
3.2 驅動防滑性能驗證

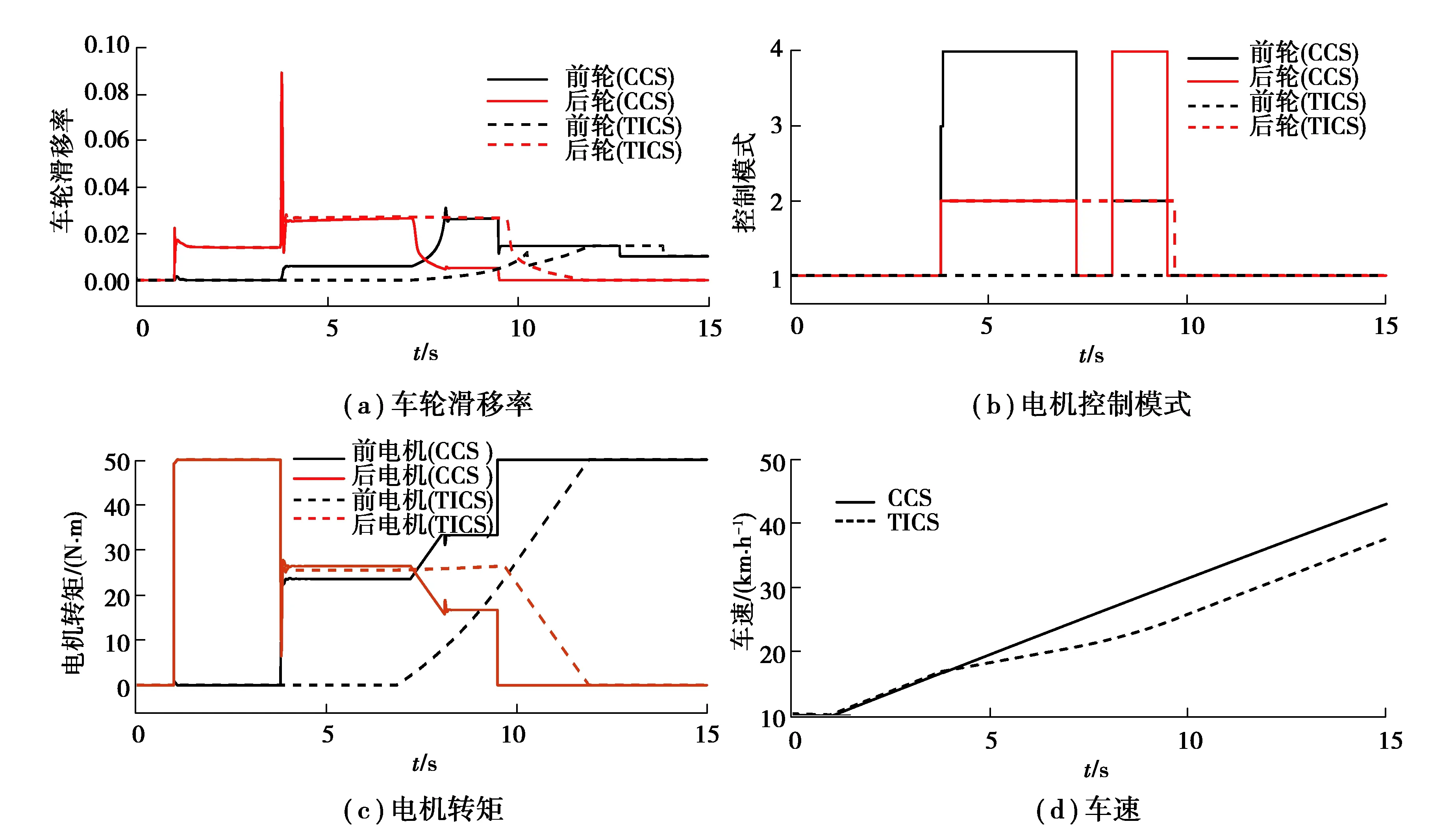
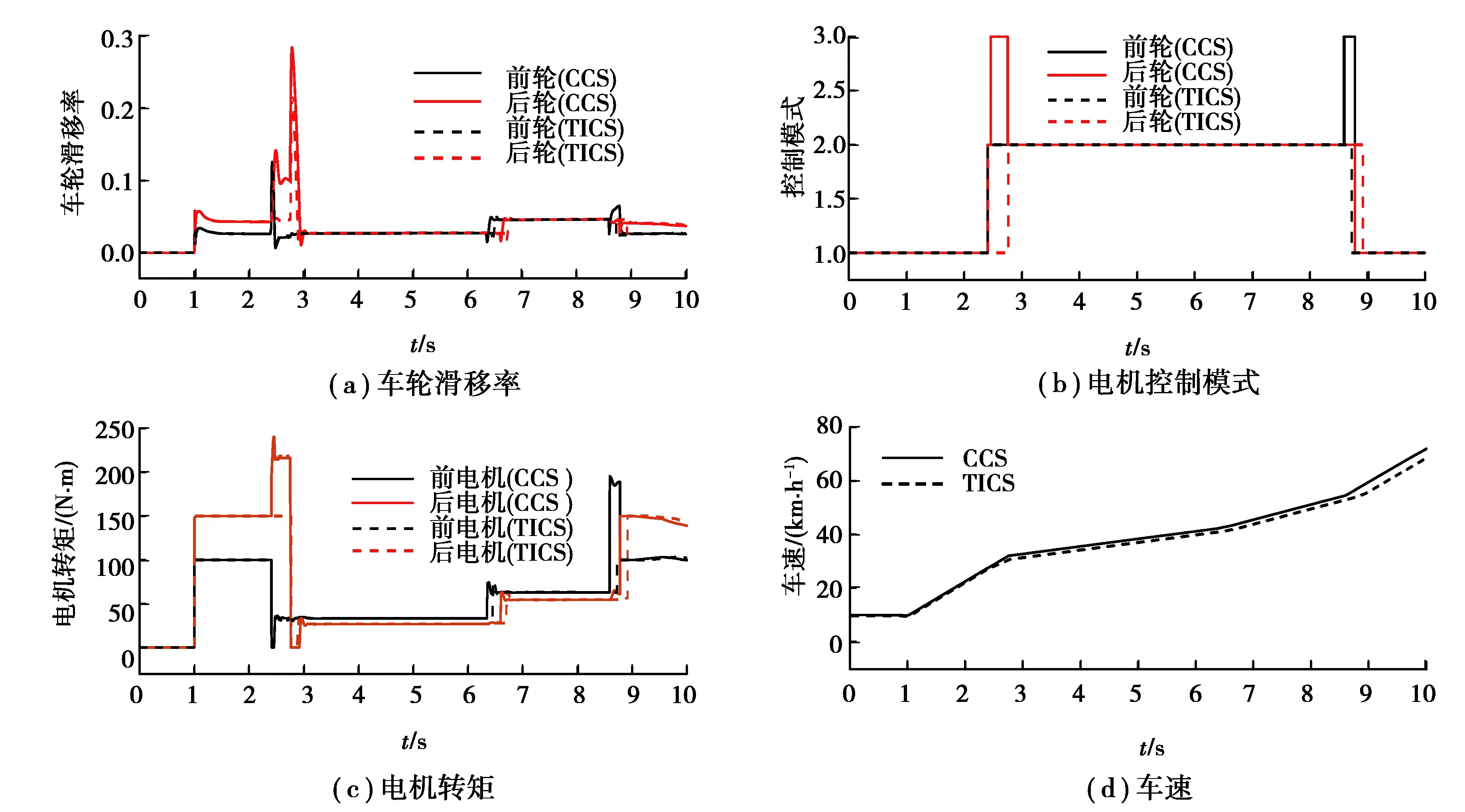
3.3 協調控制策略驗證





4 結 語

