深度學習下的數學建模思政課探究
——以不同防疫措施對新冠病毒擴散影響的分析為例

馬 芬

一、問題的提出

所謂深度學習，就是指在教師引領下，學生圍繞著具有挑戰性的學習主題，全身心積極參與、體驗成功、獲得發展的有意義的學習過程，它強調教師對作為主體的學生學習活動的引導與幫助，無論教學活動的具體形態如何，其核心是以學生為主體的主動學習活動。［1］

學科思政課是以構建全員、全程、全課程育人格局的形式，將學科課程與思想政治理論課同向同行，形成協同效應，把立德樹人作為教育的根本任務的一種教育理念。這要求數學教師要在教學中積極探索教學方式，將數學與思政相結合，有意識地回應學生在學習、生活、社交和實踐中所遇到的問題和困惑，真正觸及他們認知和實踐的隱性根源，從而對之產生積極的影響。

數學建模是對現實問題進行數學抽象，用數學語言表達問題、用數學方法構建模型解決問題的素養，在數學新課程標準中將數學建模列為六大數學核心素養之一。

2020年年初，新冠病毒開始肆虐全球，我國在中國共產黨的正確領導下，依靠制度優勢，在短短三個月內控制了國內疫情的發展，國際輿論一片嘩然，有人說我們交了一份優秀的答卷，有人說我們的防控措施侵犯了人權。中國的疫情防控宏觀決策是否合理呢？如何借用這一契機對學生進行積極引導，成為教師的一項重要任務。鑒于此，筆者組織了一節“不同防疫措施對新冠病毒擴散的影響”的數學思政課，將數學建模與思想教育落實到課堂教學中。

二、教學設計

（一）教學主題

疫情大考，彰顯制度優勢——用數學建模理性分析制度優勢。

（二）教學目標

包括：通過數學建模實踐思政育人，構建完善的數學建模過程；在建模及展示過程中，培養堅忍不拔的毅力和團結合作的精神；認識黨在抗疫中的英明、科學決策和社會主義制度優越性，進一步堅定制度自信，做到“知黨情、感黨恩、跟黨走”。

（三）課前分析

1. 影響因素

一種傳染病的傳播共有三個要素，傳染源、傳播途徑和易感人群。

2. 研究方法

依次控制這三個要素，對我國三種不同防疫措施（患者隔離、戴口罩、減少外出）分別進行研究，對比分析不同措施對疫情的影響程度。

3.模型假設

經搜索、查閱新冠疫情資料發現，每名感染者在14天內可傳染5人，假設在每一天內該感染者所接觸的人數沒有巨大差異，因而測算其每天感染其他人的數量為；假設可感染新冠病毒的人數足夠多；假設所有人感染新冠病毒的幾率相同；假設天數為n，n= 0時已經感染新冠病毒的感染者人數為t，畫圖時假設t=1000人。

4.教學環節一：小組展示匯報

（1）展示自然增長和控制傳染源模型（將確診患者隔離）

①自然增長模型：不采用任何防疫措施，稱自然增長。求得第n天累計感染人數。第n天新增感染人數。②控制傳染源模型：經查閱文獻發現，從人體攜帶病毒具有傳染性到被確診，大約是5～7天，取最快確診時間隔離，即假設第5天一早被隔離。

模型假設：患病第五天早晨被確診隔離。當0≤n≤4時，因沒有確診隔離，與自然增長相同，當n≥5時，

所以由每日新增An=Zn-Zn-1即可求解得到每日新增感染人數。

為了直觀地將控制傳染和自然增長情況對比，假設t=1000，通過Python編程畫出了累計感染人數與天數關系的函數圖象進行對比，如圖1所示，自然增長是指數型增長，速度非常快，采取隔離患者措施后，發現累計感染人數分段增長，但由圖1對比發現采用措施1比自然增長的速度慢，措施1曲線的切線斜率也比無措施曲線斜率要緩，以第6天為例，自然增長人數接近6500人，采用措施1的增長人數為5200人左右，后期差異會更加明顯。由此可見，措施1是一種有效的控制疫情的措施。

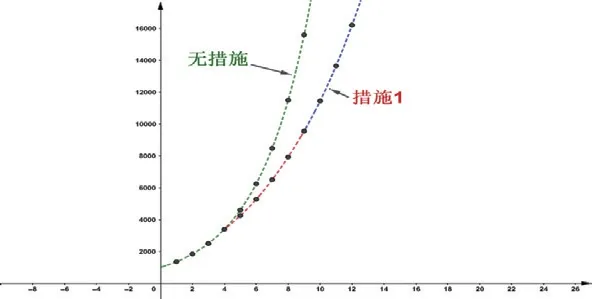
圖1

教師總結：有效但效果不夠理想，因為在患者檢測出來前，該患者已經攜帶病毒具有了傳染性，在這期間會傳染其他人。目前，我國防疫管理要求一經發現患者就要立即進行“流調溯源”，隔離密接和次密接者，從而更好地控制疫情的擴散。

（2）展示措施：切斷傳播途徑（戴口罩）

模型假設：因為2020年初武漢疫情暴發期，口罩有一段時間供應緊張，我們假設只有50%的人戴口罩；考慮到人們佩戴的方式不是特別標準，所以我們假設戴口罩完全防御病毒的效率為80%。

則原始患者傳播人由t人降為（1-50%×80%）t，平均每天每個患者傳播由降為(1 - 50% × 80%)·(1 - 50% ×，第n天累計感染人數Zn的函數關系及新增感染人數An的函數關系：

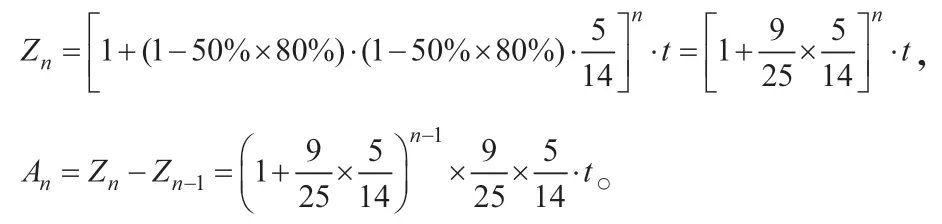
為了能清晰對比，我們在同一坐標系下畫出自然增長與措施2的累計感染人數與天數關系的函數圖象，如圖2所示。

圖2

由圖2對比發現：采用措施2戴口罩比自然增長的速度明顯減慢，仍以第6天為例，自然增長人數接近6500人，采用措施2的增長人數不到2000人，由此可見，戴口罩可以有效地控制疫情傳播速度。

教師總結：這里假設的50%與80%比例有點主觀性，我們可以用字母代替，設m%的人戴口罩；口罩的防御病毒效果為

從而進一步研究：改變模型中m、n的值，從圖象上對比m、n的值對疫情擴散的影響。

由研究發現：戴口罩可以切斷傳播途徑，有效地保護自己和他人，利用數據分析，我們可以更深刻地理解武漢疫情期間，黨中央調集各方資源加大口罩生產，號召外出佩戴口罩，這種決策的合理性。

（3）展示措施：保護易感人群（每兩天出門一次）

模型假設：假設患者在家與在外傳播的可能性相同，如果每兩天出門一次（平均每天外出總人員減半）。

所以，第n天累計感染人數第n天新增感染人數為了清晰對比，在同一坐標系下畫出自然增長與措施3的累計感染人數與天數關系的函數圖象。

由圖3對比發現：采用措施3比自然增長的速度明顯減慢，到第6天時，當天自然增長人數接近6500人，采用措施3的增長人數為2200人左右，由此可見，措施3也是一種有效的控制疫情的措施。

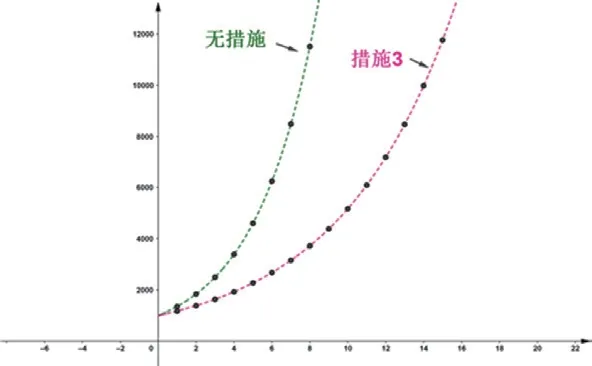
圖3

教師總結：借助數據具體分析，發現減少外出可以規避被感染的風險，而且效果顯著。

5.教學環節二：改進模型

【思考】在2020年疫情防控中，我國綜合運用了多種防疫措施，如果還在我們的模型假設下，三種防疫措施同時使用，應該如何改進模型呢？

【學生活動】小組合作，交流探究。

問題1：綜合采用3種措施，對比單一使用措施1（隔離患者），哪些量發生了改變？變成了什么？

假設患病第五天早晨被確診隔離，50%的人戴口罩，口罩的防御病毒效率為80%，并且每人每兩天出門一次，即將降為(并畫出圖象進行分析，如圖4所示。

圖4

問題2：通過圖象你能發現什么？

由圖4可以看出，當三種措施同時使用的時候，累計患者人數增加比較緩慢，說明疫情很快就會被控制。

問題3：為了更方便地看出不同防疫措施對新冠病毒擴散的影響情況，我們將四個圖象放在一起來進行對比觀察，你能得出什么結論？

【學生活動】畫圖象（圖5所示），得出結論。

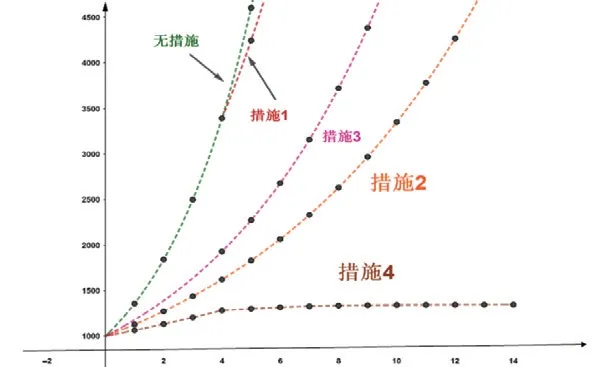
圖5

結論：結合圖象我們發現：戴口罩在三種防疫措施中貢獻率最大，措施4的效果是最好的，并且切線的斜率逐漸接近于0，也接近于控制住了疫情。

6.教學環節三：模型檢驗

【思考】在我們做出合理假設的情況下，構建了數學模型，這種模型是否合理？能否解決實際問題呢？

回溯武漢疫情數據，2020年2月13日公布新增數據為13436人，按照我們的假設：這部分新增人數是在2月9號感染病毒且具有傳染性，所以我們選擇初始數據t=14000，利用Python編程畫出三種措施同時使用下的每日新增人數函數圖象，畫出第5天到第19天的分析圖象，如圖6所示。

圖6

從2月9日起計，19天后，大約3月1日或3月2日基本可以達到當日無新增。而當日實際新增數據為：2月28日，420人；3月1日，193人；3與2日，111人；3月9日，17人。

問題4：你能分析一下模型數據與實際數據不完全吻合的原因嗎？

從3月1日起，新增比例明顯減少，但并沒有到0。原因是我們研究的模型是理想化的，而實際情況比較復雜。

（四）課堂小結

通過數學建模，利用數據理性分析表明我國的防疫措施是正確的，中國的抗疫維護了人民的生命安全和身體健康，體現了對每一個生命最好的尊重，充分體現了以人民為中心的制度優勢，這本身就是最大的人權、真正的尊重人權，借助數據有力回擊了“侵犯人權”的歪曲事實的說法。

三、教學反思

（一）引領深度學習，注重知識生成過程

本節課通過有思維含量的問題和有效的學生動手實踐活動，引領學生深度學習，具體體現在以下三個方面：一是課前組織學生成立研究小組，討論、分析影響疫情擴散的相關因素及模型假設；二是課前模型建構的指導，比較復雜的模型建構，學生的思維層次難以達到所要求的高度，需要教師引導點撥；三是課堂上引導學生進行模型檢驗，利用真實數據驗證自己構建模型的可行性。

（二）引領深度學習，提升建模素養

深度學習在于幫助學生去“親身”經歷知識的發現和建構過程，本節課教師引領學生經歷了數學建模的全過程，在經歷了選題、開題到做題這一較為完整的建模過程之后，每個學習小組對自己的建模過程進行了完整的梳理和反思。學生梳理研究成果，表達、展示研究成果，是對數學模型、模型求解進行陳述，需要學生完成對實際問題的合理刻畫，掌握簡潔性、準確性數學語言；對模型求解的檢驗和形成結論，需要學生有自主性分析和適用性解讀。在此過程中能提升學生對問題的抽象概括能力，有效提升了學生數學建模核心素養。

（三）引領深度學習，實現立德樹人

深度學習是以實現立德樹人為根本目的，培養和發展學生的核心素養，促進學生全面發展；深度學習的“深”，是觸及學生心靈深處，與人的理性、情感、價值觀密切相連。本節課從社會熱點、實際問題入手，通過數據理性驗證我國防疫措施的合理性，進一步使學生從心靈深處體認我國社會主義制度的優越性，中國共產黨領導下的政府防疫抗疫政策措施的正確性、科學性，學生自己用數據辨明了網上的不實謠言，達到了潤物無聲、潛移默化的思政育人境界。所以，本節課的教學深在學生的精神，深在學生的心靈。