感應電機磁鏈與轉矩無差拍控制*
李耀華, 陳桂鑫, 王孝宇, 劉子焜, 劉東梅, 任 超
(長安大學 汽車學院,陜西 西安 710064)
0 引 言
有限狀態集模型預測控制(FCS-MPC)性能優越、控制靈活,是電機控制領域的研究熱點[1-2]。文獻[3-5]將模型預測控制應用于感應電機,將逆變器的基本電壓矢量遍歷代入磁鏈和轉矩預測模型,基于成本函數選擇最優電壓矢量。模型預測轉矩控制(MPTC)選擇的電壓矢量作用時間固定,可與無差拍控制結合,優化電壓矢量作用時間,提高系統性能。文獻[6-11]將轉矩無差拍控制與MPTC結合,以減小轉矩脈動,但該策略僅考慮轉矩無差拍控制,磁鏈控制依然需要模型預測控制,并且系統要進行無差拍控制和模型預測控制,計算量較大。本文提出感應電機磁鏈和轉矩無差拍控制,仿真和實時性試驗表明,相比于MPTC和轉矩無差拍模型預測控制,所提策略在控制性能和實時性上均具備優越性。
1 感應電機MPTC
靜止兩相α-β坐標系下,以定子磁鏈矢量ψs和定子電流矢量is為狀態變量,定子電壓矢量us為輸入變量,三相感應電機狀態方程如下:
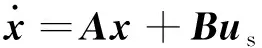
(1)
感應電機轉子磁鏈矢量ψr和電機轉矩Te如下:

(2)

(3)
采用一階歐拉向前離散公式對式(1)離散化,則可得下一時刻定子電流矢量和定子磁鏈矢量預測模型如下:

(4)
ψs(k+1)=ψs(k)+Tsus(k)-TsRsis(k)
(5)
將下一時刻定子電流矢量和定子磁鏈矢量代入式(3),可得下一時刻轉矩如下:

(6)
兩電平三相逆變器可產生7個基本電壓矢量,如式(7)所示。其中零電壓矢量可由000或111兩種開關狀態生成,具體選擇以開關次數最小為原則[12]。
us∈{u0,u1,u2,u3,u4,u5,u6}
(7)
基于當前時刻定子電流矢量、定子磁鏈矢量和轉子磁鏈矢量,感應電機模型轉矩控制系統將逆變器電壓矢量遍歷代入定子磁鏈矢量、定子電流矢量和轉矩預測模型,則可得到下一時刻定子磁鏈和轉矩。
定義表征磁鏈和轉矩控制性能的成本函數如下所示[13]:

(8)
將磁鏈和轉矩預測值代入式(8),并輸出令成本函數最小的電壓矢量,從而實現MPTC。感應電機MPTC系統如圖1所示。
2 轉矩無差拍模型預測控制
由MPTC原理可知,系統通過成本函數定量評價7個電壓矢量在一個采樣周期對磁鏈和轉矩的控制效果,并從這7個電壓矢量中選擇相對最優電壓矢量,但這只是被動選擇相對最優,并未根據系統期望值主動計算絕對最優。因此,可基于轉矩誤差優化電壓矢量作用時間,計算得到理想占空比,實現轉矩無差拍控制,從而減小轉矩脈動。
將式(3)所示轉矩方程對時間求導可得:

(9)
將式(1)所示的定子電流矢量和定子磁鏈矢量代入式(9)以替換等號右側的微分項,并采用一階歐拉向前公式將等號左側的轉矩導數離散化可得:

(10)
由于au含電壓變量,將其作用時間設為tu。對于每個采樣時刻,a0為常數項,作用時間設置為Ts,可得:
Te(k+1)-Te(k)=Tsa0+tuau
(11)
根據轉矩無差拍原理,可得:

(12)
將當前時刻的轉矩參考值近似為下一時刻轉矩參考值,可得:

(13)
因此,實現轉矩無差拍的電壓矢量理想占空比如下:

(14)
將電壓矢量遍歷代入式(14),則可得到對應的理想占空比。如果計算得到占空比d小于0,表明該電壓矢量對轉矩的增減效果與無差拍控制相反,應予以舍棄,不進行下一步模型預測控制計算。如果得到占空比d大于1,表明該電壓矢量在一個采樣周期內無法實現轉矩無差拍控制,令占空比為1。這里需要指出:零電壓矢量的作用時間必為采樣周期,無需轉矩無差拍控制計算占空比,直接令d等于1。
由于轉矩無差拍控制并未考慮磁鏈控制,且并不是所有的電壓矢量都可實現轉矩無差拍控制。因此,需要將占空比調整過的電壓矢量代入磁鏈和轉矩預測模型,計算下一時刻的磁鏈和轉矩預測值,通過如式(8)所示的成本函數選擇最優的優化電壓矢量。
感應電機轉矩無差拍模型預測控制系統如圖2所示。
3 磁鏈和轉矩無差拍控制
由上文可知,轉矩無差拍模型預測控制僅對轉矩進行無差拍控制,磁鏈依然采用模型預測控制,使得磁鏈脈動較大。因此,下文提出感應電機磁鏈和轉矩無差拍控制。
由式(5)可知,忽略定子電阻壓降,定子磁鏈坐標系下,施加電壓矢量us一個采樣周期后,下一時刻的定子磁鏈矢量ψs如圖3所示,其中α為施加電壓矢量與定子ψs(k+1)磁鏈矢量的夾角,Δθs為定子磁鏈矢量角度的變化。
由圖3可知,施加電壓矢量引起的定子磁鏈矢量角度變化Δθs如下:

(15)
令q=usTs/ψs,式(15)可簡寫為

(16)
由于采樣周期很小,q值較小。當0°<α≤360°、0 由圖4和圖5可知,此時定子磁鏈矢量角度的變化較小,cos(Δθs)≈1。因此,下一時刻定子磁鏈幅值可簡化為 ψs(k+1)≈ψs(k+1)cos(Δθs) (17) 由圖3可得: ψs(k+1)cos(Δθs)=ψs(k)+usTscosα (18) 設定子磁鏈矢量與靜止坐標系α軸夾角為αψ,施加電壓矢量與α軸夾角為αu,則可得: α=αu-αψ (19) 由此可得: usTscosα=usTscos(αu-αψ)= usTs(cosαucosαψ+sinαusinαψ) (20) 電壓矢量和定子磁鏈矢量在靜止坐標系α-β軸的分量如下: (21) (22) 將式(20)~式(22)代入式(18),可得: (23) 由磁鏈無差拍控制可知: (24) 由此可得: (25) 由上文轉矩無差拍控制可得: Te(k)+Tsa0+Tsau=Te(k)+Tsa0+ (26) 聯立式(25)與式(26),則可求得滿足磁鏈和轉矩無差拍控制的理想電壓矢量在靜止坐標系β軸分量usβ如下: usβ= (27) 將usβ代入式(25),則可求得理想電壓矢量在靜止坐標系α軸的分量usα如下: (28) 在得到滿足磁鏈和轉矩無差拍控制的理想電壓矢量后,同樣采用空間矢量調試技術生成。感應電機磁鏈和轉矩無差拍控制系統如圖6所示。 表1 電機仿真系統參數 感應電機MPTC仿真波形如圖7~圖10所示。感應電機轉矩無差拍模型預測控制仿真波形如圖11~圖14所示。感應電機磁鏈和轉矩無差拍控制仿真波形如圖15~圖18所示。 定義轉矩脈動均方根誤差(RMSE)和磁鏈脈動RMSE如下: (29) (30) 式中:m為采樣個數。 不同控制策略下,0.2~8 s(不含電機軟啟動)轉矩脈動RMSE、磁鏈脈動RMSE和定子電流總諧波失真(THD)如表2所示。 表2 控制性能 由仿真結果可知: (1) MPTC、轉矩無差拍模型預測控制與磁鏈和轉矩無差拍控制下,電機系統均可實現四象限正常運行; (2) 相較于MPTC,轉矩無差拍模型預測控制可降低轉矩脈動和磁鏈脈動,轉矩脈動RMSE降低88.61%,磁鏈脈動RMSE降低32.61%,電流THD降低41.89%; (3) 相較于MPTC,磁鏈和轉矩無差拍控制可顯著降低轉矩脈動和磁鏈脈動,轉矩脈動RMSE降低87.84%,磁鏈脈動RMSE降低97.83%,電流THD降低94.21%。與轉矩無差拍模型預測控制相比,轉矩脈動略有增大,但磁鏈脈動顯著降低,磁鏈脈動RMSE降低96.77%,電流THD降低90.03%。 為了驗證不同控制策略的實時性,基于 STM32H7單片機平臺對MPTC、轉矩無差拍模型預測控制、磁鏈和轉矩無差拍控制進行單步實時性驗證。不同控制策略的實時性驗證測試用例參數如表3所示。 表3 測試用例參數 對以上3種控制策略進行單步運算循環8萬次,不同算法執行時間如表4所示。 表4 算法程序運行時間 由表4可知,MPTC計算耗時最多,轉矩無差拍模型預測控制次之,磁鏈和轉矩無差拍控制計算耗時最少,為MPTC的4.79%、轉矩無差拍模型預測控制的5.29%。 (1) MPTC、轉矩無差拍模型預測控制、磁鏈和轉矩無差拍控制下,感應電機系統均可實現四象限正常運行。 (2) 相比于MPTC和轉矩無差拍模型預測控制,磁鏈和轉矩無差拍控制可顯著降低轉矩脈動和磁鏈脈動。 (3) 磁鏈和轉矩無差拍控制計算簡單,實時性好。與MPTC相比,計算耗時減少95.21%,與轉矩無差拍模型預測控制相比,計算耗時減少94.71%。







4 仿真驗證





5 實時性驗證


6 結 語

