PSO 聯(lián)合Kriging 模型的結(jié)構(gòu)可靠度計(jì)算

解豐銘， 溫 馨

（遼寧石油化工大學(xué)， 遼寧 撫順 113001）

引言

隨著學(xué)者們的努力探究，結(jié)構(gòu)可靠度算法在不斷的創(chuàng)新發(fā)展。響應(yīng)面法作為最經(jīng)典的代理模型法，以減少抽樣次數(shù)、提高擬合效率、增加計(jì)算精度為目標(biāo)，使用二次多項(xiàng)式作為回歸擬合方程，具有較好效果。但是用于非線性程度較高的功能函數(shù)時(shí)，會(huì)產(chǎn)生結(jié)果不收斂的情況。Kriging 方法可以有效彌補(bǔ)上述不足，不但突破了經(jīng)典插值和統(tǒng)計(jì)學(xué)的限制，綜合考慮了變量的確定性和隨機(jī)性，而且與經(jīng)典響應(yīng)面方法相比具有算法靈活、可獲得待求點(diǎn)的無(wú)偏最優(yōu)估計(jì)等優(yōu)點(diǎn)[1]。

Kriging 思想最早是由南非的礦業(yè)工程師Krige提出的，隨后一位法國(guó)數(shù)學(xué)家Matheron[2]對(duì)其成果進(jìn)行理論系統(tǒng)化分析，提出一種插值外推理論。Giunta和Watson[3]用自變量測(cè)試比較了最小二乘法建立的二次多項(xiàng)式和Kriging 插值法建立的代理模型，結(jié)果后者更具靈活性和計(jì)算效率。2011 年陳志英等[4]將粒子群優(yōu)化算法用于Kriging 建模，以其良好的群體搜索能力保證了相關(guān)參數(shù)的最優(yōu)性。2016 年，黃曉旭[5]提出Kriging 模型代替結(jié)構(gòu)功能函數(shù)，引入主動(dòng)學(xué)習(xí)函數(shù)，在每次迭代中加入最佳樣本點(diǎn)更新Kriging 模型，能夠得到精度較高的可靠度結(jié)果。

1 拉丁超立方設(shè)計(jì)（LHD）

樣本點(diǎn)的選擇對(duì)代理模型的精度有很大的影響，拉丁超立方抽樣（LHS）由于全空間填充和非重疊采樣特性成為最合適搭配Kriging 的抽樣方法。

M 水平N 因子的LHS 構(gòu)造方法：

1）對(duì)每個(gè)維度空間進(jìn)行M 等分，形成區(qū)間：[0，1/M]，[1/M，2/M]，…[1-1/M，1]。

2）在隨機(jī)變量的均值加減3 倍標(biāo)準(zhǔn)差范圍內(nèi)（也稱3σ 準(zhǔn)則）隨機(jī)選取每個(gè)區(qū)域的樣本點(diǎn)，得到x1（k）、x2（k），…，xM（k）。

3）依照維度選取分量隨機(jī)配對(duì)，不考慮已選取過(guò)的分量，組成M 個(gè)N 維數(shù)據(jù)。

圖1 為一個(gè)六水平二因子的拉丁超立方抽樣概念圖，可明顯看出其優(yōu)點(diǎn)：每個(gè)采樣點(diǎn)的橫縱網(wǎng)格都沒(méi)有交叉重復(fù)，具有獨(dú)立性、隨機(jī)性和均勻性，可為后續(xù)近似模型擬合起到很好的鋪墊作用。

2 Kriging 模型

Kriging 模型的數(shù)學(xué)表達(dá)式如下：

式中：p 為回歸量的個(gè)數(shù)；x 為抽樣點(diǎn)，z（x）是隨機(jī)過(guò)程Z（x）的模型。表達(dá)式整體由兩部分組成，前半部分是線性回歸模型，反映過(guò)程均值的變化，提供模擬的全局近似。回歸量的選擇對(duì)于模擬的精度不起決定性的作用，因此在大多數(shù)工程中為簡(jiǎn)化模型常取常量1[6]。后半部分，z（x）服從正態(tài)分布N（0，σ2）但不獨(dú)立，其樣本點(diǎn)之間的協(xié)方差非零且關(guān)系如下：

公式（2）中R（θ，ω，x）是一個(gè)空間相關(guān)函數(shù)，其中θ 是一個(gè)以高斯模型為基礎(chǔ)的關(guān)鍵參數(shù)，ω 是模型的光滑程度參數(shù)。可整理為式（3）：

標(biāo)準(zhǔn)Kriging 模型空間相關(guān)函數(shù)為高斯模型如式（4）所示：

式中：d 是兩數(shù)據(jù)間距量。利用已知樣本點(diǎn)的空間函數(shù)響應(yīng)值組成相關(guān)矩陣：

Kriging 模型的最佳線性無(wú)偏估計(jì)如式（6）所示：

式（6）的方差估計(jì)值可以由式（7）計(jì)算：

根據(jù)式（3）、式（6）、式（7）可知，矩陣R、估計(jì)因子β^與模型的估計(jì)方差都由參數(shù)θ 決定，基于最大似然估計(jì)理論，利用無(wú)約束優(yōu)化方法最大化式（8）可得到最優(yōu)θ 值。

Kriging 模型的建立問(wèn)題最后變成了非線性無(wú)約束的優(yōu)化問(wèn)題。θ 值越接近最優(yōu)值，模型的效果就會(huì)越好。在Matlab 軟件中也可以通過(guò)Dace 工具箱建立簡(jiǎn)單的Kriging 模型。

3 PSO 算法

粒子群優(yōu)化算法（PSO）：一種全局尋優(yōu)算法，與傳統(tǒng)算法相比具有計(jì)算快、全局搜索能力強(qiáng)、受初始種群規(guī)模限制小等特點(diǎn)。

算法具體流程如下：初始化粒子的速度和位置、計(jì)算適應(yīng)度、記錄個(gè)體最優(yōu)數(shù)值和群體歷史最優(yōu)值、更新速度和位置、檢查是否滿足條件，滿足則輸出，不滿足則從第一步繼續(xù)開(kāi)始。

迭代過(guò)程的公式為：

式中：ω 為慣性權(quán)重；ω×Vid表示粒子保持之前運(yùn)動(dòng)速度的趨勢(shì)，即慣性；C1、C2表示記憶參數(shù)；r1、r2為隨機(jī)數(shù)控制粒子速度在限制范圍。Pid、Pgd為局部極值全局極值，x 表示位置坐標(biāo)。

4 結(jié)合優(yōu)化算法的代理模型可靠性分析

結(jié)構(gòu)在規(guī)定的時(shí)間內(nèi)，在規(guī)定的條件下，完成預(yù)定功能的概率，稱為結(jié)構(gòu)可靠度。可靠度的符號(hào)表示為‘β’，也叫做可靠度指標(biāo)，是分析可靠性時(shí)的重要參數(shù)。可靠度的幾何意義是在標(biāo)準(zhǔn)化正態(tài)空間中坐標(biāo)原點(diǎn)到極限狀態(tài)函數(shù)曲面的最短距離（也就是坐標(biāo)原點(diǎn)到設(shè)計(jì)驗(yàn)算點(diǎn)的最短距離），其值越大結(jié)構(gòu)越可靠。

編寫(xiě)Matlab 程序時(shí)需要將幾何意義定為罰函數(shù)的一個(gè)約束條件，另外還要滿足極限狀態(tài)要求，即極限狀態(tài)方程為0。罰函數(shù)可在求解最優(yōu)化問(wèn)題時(shí)對(duì)不滿足約束點(diǎn)或企圖逃離可行域點(diǎn)賦予一個(gè)很大的增量，其目的是更高效的區(qū)分可行與不可行值。

PSO 算法結(jié)合代理模型進(jìn)行可靠性分析的基本思想是：

1）首先用LHD 的3σ 準(zhǔn)則抽取樣本點(diǎn)，記錄樣本和響應(yīng)值。

2）通過(guò)Matlab 軟件和上一步的數(shù)據(jù)擬合Kriging模型得到近似隱式的極限狀態(tài)曲面。

3）利用尋優(yōu)算法PSO 結(jié)合罰函數(shù)理論編程，尋找設(shè)計(jì)驗(yàn)算點(diǎn)。

5 算例

圖2 為Matlab 軟件擬合的Kriging 模型，圖3 為PSO 算法求解非線性等式約束的兩個(gè)最優(yōu)值（最短距離2.91 和極限方程為0），最后標(biāo)準(zhǔn)正態(tài)化得可靠度2.25，其他算法求解結(jié)果見(jiàn)下頁(yè)表2。

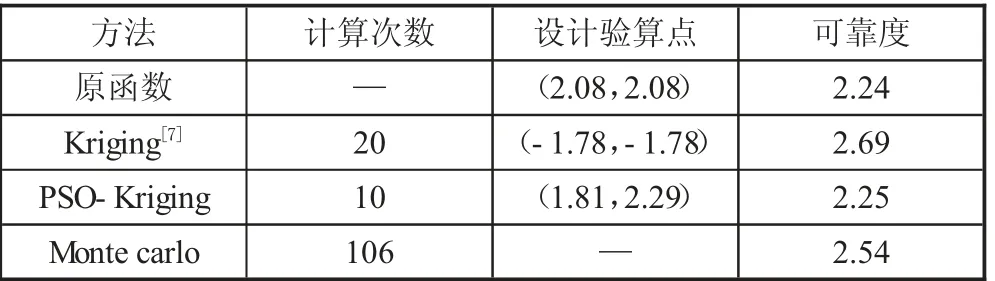
表2 各計(jì)算方法結(jié)果對(duì)比

此題設(shè)計(jì)驗(yàn)算點(diǎn)附近的曲率較大，一般求解方法不收斂且需要多次計(jì)算。

6 結(jié)論

對(duì)比于傳統(tǒng)的Kriging 法和蒙特卡洛法，PSO-Kriging 無(wú)論是在計(jì)算效率還是精度上都要更加優(yōu)秀。與尋優(yōu)算法的結(jié)合使用讓收斂效率大幅提高，不但可以明顯減少計(jì)算次數(shù)，還能在極限狀態(tài)方程非線性程度較高時(shí)保持準(zhǔn)確性。