基于改進BIT算法的農業機器人路徑優化研究

陸宇豪1，劉義亭2,3，郁漢琪4，余 偉5

（1.南京工程學院 研究生院，南京 211167；2.南京工程學院 自動化學院，南京 211167；3.東南大學 信息科學與工程學院，南京 210096；4.南京工程學院 工業中心，南京 211167；5.華齡和平南京智能科技有限公司，南京 210000）

0 引言

路徑規劃技術作為農業機器人領域的重要技術，其目的在于尋找源與目標之間的最佳路徑，并要求路徑安全無碰撞、算法收斂速度快[1]。目前，路徑規劃算法種類較多，主要有基于圖搜索的A星（A-star）算法和基于采樣的快速搜索隨機樹（Rapidly Exploring Random Trees，RRT）算法。

其中，以A星為代表的基于圖搜索的路徑規劃算法主要是通過設定合適的啟發函數指導柵格點的搜索，從而獲取最優路徑[2]。此類算法在小地圖環境下響應極快，且生成路徑最短。但在農業大場景下，A星算法的計算量會迅速上升，搜索效率降低，且實時性差。

以RRT為代表的基于采樣的路徑規劃算法主要通過對空間點進行隨機采樣，將初始點作為隨機樹的根節點，在約束條件下擴展隨機樹并最終形成一條連通路徑[3]。此類方法無需對地圖進行預處理，適用于大型平面或高維空間的路徑搜索，搜索速度較快，但在沒有適當采樣指導的情況下搜索較為盲目，性能不穩定且耗時較長，獲取的路徑也并非最優[4]。

針對上述A星算法與RRT算法的優缺點，Jonathan D. Gammell提出了一種將圖搜索和隨機采樣思想相結合的批量通知樹（Batch Informed Trees，BIT）算法[5]。該算法能夠在獲得移動成本最優路徑的同時避免大空間環境下搜索效率低、實時性差的問題[6,7]，但并未考慮行車的安全問題，且生成的路徑折角較多，并不符合機器人的實際運動需求。因此，在BIT算法的基礎上增加障礙物膨脹與曲線優化，進而提升機器人移動的安全性和穩定性。

1 BIT算法原理

1.1 BIT算法基本原理

與傳統的基于圖搜索的A星算法與基于隨機采樣的RRT算法均不同，BIT算法結合兩者優勢，其首先對自由空間進行隨機采樣，利用采樣點、起點與終點構建起隱式隨機幾何圖（Random Geometric Graph，RGG），隨后通過啟發式搜索擴展搜索樹，在成功找到路徑后，縮小采樣范圍。與RRT相比，其構造樹的過程不直接對邊進行碰撞檢測，而是只有當邊線為隊列最佳邊時，才對其進行碰撞檢測，由此減少非必要的運算[8]，同時在每次批量采樣前，對搜索樹進行修剪，刪去無助于提高路徑成本的節點與邊線，進而極大提升算法的運算速度和收斂速度。其主體的偽代碼見表1，其主要包括批量采樣、擴展及修剪樹模塊等，詳細步驟可見參考文獻[5]。

1.2 數學約定

為便于算法講解，對Alg1中的相關參數進行數學約定。

Alg1.Line1:SettingUpPlanning()為初始化函數，該函數所涉及的數學約定，QE為有序連線集合，其序列第一個元素表示代價值最小的邊及其代價值。QV為有序節點集合，其序列第一個元素表示代價值最小的節點及其代價值。E為樹模型中的連線集合，E集合中的每個元素用(v,w)表示，且v,w∈V。V為樹模型中的頂點集合。φ為空集；xstart表示起點坐標；xgoal表示終點坐標；Xsamples為采樣點集合；r為隱式RGG算子。

Alg1.Line4:gT(xgoal)為根據隨機樹搜索路徑到達目標點所需的代價。

Alg1.Line5:m為每次采樣點的個數，表示集合的并操作。

Alg1.Line6:Vold為舊頂點集合。

Alg1.Line7:Vnum表示V集合元素的個數，Xsamplesnum表示Xsamples集合元素的個數。

Alg1.Line10:vm、xm表示邊隊列中代價值最小邊對應的兩個頂點。

Alg1.Line13-22:g'(v)為v點與起始點的歐拉距離；c'(v,x)為v點與x點之間的歐拉距離；h'(x)為x點與終點的歐拉距離；c(vm,xm)為vm點與xm點之間的實際距離（包含碰撞檢測）。

1.3 BIT算法程序實現

BIT算法偽代碼見表1。

表1 BIT算法偽代碼Table 1 BIT Algorithm pseudo code

首先對算法進行初始化操作，將QE、QV、E置空，起始點xstart插入V，目標點xgoal加入采樣點集合Xsamples，并設置r=∞（Alg.1,Line1）。

隨后進入循環，若QV和QE為空，則進入修剪樹(Alg.1，Line4)和批量采樣(Alg.1，Line5)步驟。

修剪與批量采樣完成后，將當前頂點集合加入Vold中進行記錄，并將頂點集V加入QV頂點隊列進行排序，隊列最前端元素為代價值最小的頂點及其代價(Alg1.Line6)。

之后，計算r算子(Alg1.Line7)，其可通過式（1）計算獲得：

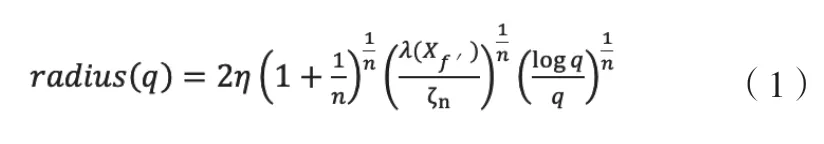
式（1）中：λ()——一個集合的勒貝格測度。

Xf '——{x∈X│f '(x)≤cbest}。

n——求解空間的維度。

ζn——n維單位球的勒貝格測度。

q——Vnum+Xsamplesnum。

Vnum——V集合元素的個數。

Xsamplesnum——Xsamples集合元素的個數。

η——自適應調整參數，η≥1。

bestVertexValue與bestEdgeValue分 別 返 回QE、QV隊列中的最小代價值及其對應的頂點和邊，只要滿足循環條件，則持續對頂點隊列中代價值最小的點進行擴展，隨后提取邊隊列中的最優邊(vm,xm)，將其從QE隊列中刪除(Alg1.Line8-11)。

CheckValues(vm,xm)用于檢驗獲得的(vm,xm)邊是否滿足gT(vm)+c'(vm,xm)+h'(xm)＜gT(xgoal)、g'(vm)+c(vm,xm)+h'(xm)＜gT(xgoal)、gT(vm)+c(vm,xm)＜gT(xgoal)3個擴展條件，若均滿足則檢查點xm是否已在樹中，若樹中已存在點xm，則將E中所有與xm相連的邊(v,xm)去除(Alg1. Line14)；若xm不在樹中，則從采樣點集合Xsamples中刪除點xm，并將點xm加入V、QV中(Alg1.Line16-Line17)。隨后將邊(vm,xm)加入集合E，遍歷QE中以xm為終點的邊，若滿足gT(v)+c'(v,xm)≥gT(xm)，則將(v,xm)從QE中刪除(Alg1.Line18-19)。

若不滿足Alg1.Line12，則表示所有的采樣點都不可能對當前解進行優化，則將QE、QV置空，隨后進入Alg1.Line2重新采樣計算(Alg1.21)。

在滿足結束要求后，返回求解出的搜索樹T(V,E)（Alg1.Line22-23）。

1.4 修剪樹

修剪樹模塊的函數為Prune(gT(xgoal))。gT(xgoal)為根據搜索樹路徑到達目標點的實際代價。該步驟旨在去除搜索樹中對優化解無用的點和邊，以提升搜索效率，減少搜索的盲目性，其主要為剔除采樣點集合、樹頂點集合和樹連線頂點集合中從起點經過該點到達目標點所需預估代價大于當前最優路徑代價的點。

1.5 擴展

擴展模塊的函數為expandVertex(v)，表示對v頂點進行擴展操作。其首先將bestInVertexValue()函數所獲得的最小代價值點v從隊列QV中取出，后計算采樣點中與點v的歐拉距離小于r的臨近點集合。遍歷臨近點集合，若此臨近點x與點v的連線能夠滿足g'(v)+c'(v,x)+h'(x)＜gT(xgoal)，則將兩點連線所形成的邊插入隊列QE。

1.6 批量采樣

Sample(m,gT(xgoal))為批量采樣功能函數，其在未找到可行路徑狀態下在全地圖自由空間進行批量采樣，在通過搜索樹成功尋找到路徑后，則縮小采樣范圍，轉變為在橢圓區域的自由空間內進行采樣。其橢圓采樣空間的計算方法如圖1。

圖1 橢圓采樣空間Fig.1 Elliptical sampling space

長軸為cbest,為當前到達目標點的最優路徑長度，短軸的計算方法為，cmin為起始點與目標點間的歐拉距離，在實際運算中，可先在標準圓中進行采樣，并對采樣點進行矩陣運算，使其平移旋轉至橢圓區域。

此方法能夠在尋找到初始解后有效地提升算法收斂速度。

2 Bezier曲線優化

在路徑規劃過程中，通常會產生一條具有多個銳角或拐角的路線，這種路徑不適合實際作業中攜帶大量物品的移動機器人[9]。因此，為了使搬運機器人能夠更加穩定地完成其任務，需要對生成的路徑進行平滑處理。

Bezier曲線是一種通過較少控制點便能生成復雜平滑路徑的方法，目前被廣泛應用于汽車車體工業設計、計算機輔助設計、路徑規劃等領域。以二階貝塞爾曲線為例，其生成過程如圖2。

為便于理解，圖2選取5個特殊比例來求解其對應的貝塞爾曲線點，在實際運算中，其選取線段長度與對應邊長度的比例為t(t∈[0,1])，可以取無窮多個，從而形成整條貝塞爾曲線。

圖2 二階貝塞爾曲線生成過程Fig.2 Generation process of third-order Bessel curve

如圖2所示，Pi(i=0,1,2)為形成貝塞爾曲線所需要的控制點，Li(i=0,1,…,3)為線段P0P1上的點，Ki(i=0,1,…,3)為線段P1P2上的點，Ti(i=0,1,…,3)為貝塞爾曲線上的點，其幾何關系滿足：

擴展到一般情況，其數學表達式如式（2）、式（3）表示：

式中：n——擬合點個數。

t——線性插值比例，t∈[0,1]。

i——i∈{0,1,…,n}。

由式（2）、式（3）可得，一階Bezier曲線的表達式為：

二階Bezier曲線為：

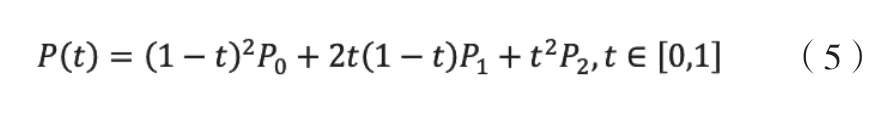
三階Bezier曲線為：

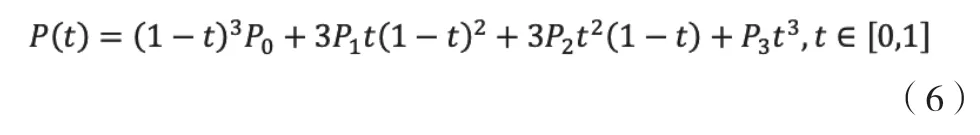
式中：Pi——第i個點。

k階Bezier曲線需要k+1個點進行求解。在實際運用中，隨著Bezier曲線階數的增加，其運算復雜度呈幾何倍增長，而三階Bezier曲線能夠保證機器人運行時其速度、加速度均為連續的同時，又不會嚴重影響運算速度，符合機器人的運動控制要求，因此采用三階Bezier曲線對點進行擬合。

將三階Bezier曲線進行擬合優化,則優化后的曲線點為：

式（7）中：xi——第i點的x坐標。

yi——第i點的y坐標。

x、y表示Bezier曲線的擬合點坐標。

三階貝塞爾曲線優化與BIT結合的具體算法步驟見表2。

表2 Bezier曲線優化偽代碼Table 2 Bezier curve optimization pseudo code

3 仿真實驗與結論

在Intel i7-6700HQ筆記本電腦上使用Python 3.9，并在Anaconda3環境下對原始BIT算法、障礙物膨脹及其Bezier曲線優化后的算法進行仿真實驗。

本文路徑規劃的障礙物仿真環境如圖3，其為幾何地圖，總尺寸為240m×240m，地圖中心為原點坐標(0,0)，xstart=(-95,-95)，xgoal=(60,85)，每批次采樣點個數200個，r算子η系數為1.1，障礙物膨脹度為5m。本文以圓形機器人為仿真模型，其半徑為R，使機器人以1m/s的速度嚴格沿生成路徑行駛。通常情況下，障礙物的膨脹度應略大于機器人的半徑R，以此保證機器人在沿路徑行駛的過程中不會發生碰撞。

其中，圖3左下方為起點xstart,右上方為目標點xgoal，地圖中的圓形障礙物以(x,y,r)形式進行表示。其中，x、y為圓心坐標，r為半徑。

圖3 障礙物分布Fig.3 Obstacle distribution

圖4為BIT未經過障礙物膨脹和曲線優化，運行迭代10000次后生成的路徑，其生成路徑與障礙物距離過近，多個障礙物與路徑相切，因此在實際環境中無法滿足機器人安全行駛的需求。

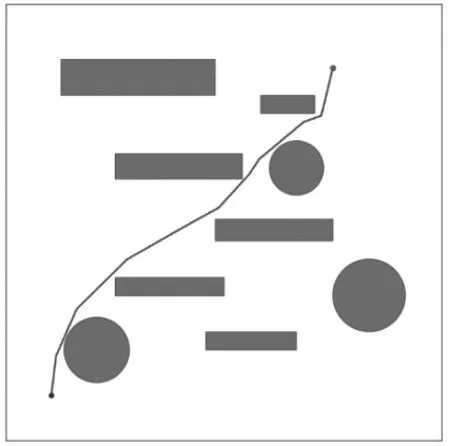
圖4 原算法路徑圖Fig.4 Original algorithm path diagram

因此，對障礙物進行膨脹操作，膨脹后的障礙物地圖如圖5。

圖5 膨脹地圖Fig.5 Expansion map

圖6為對地圖障礙物向外膨脹5m后，算法運行迭代10000次后生成的路徑。由圖6可知，其求解出的路徑距離障礙物均大于5m，雖然能夠滿足機器人運行的安全性，但仍存在一定折角。

圖6中的路徑坐標見表3。

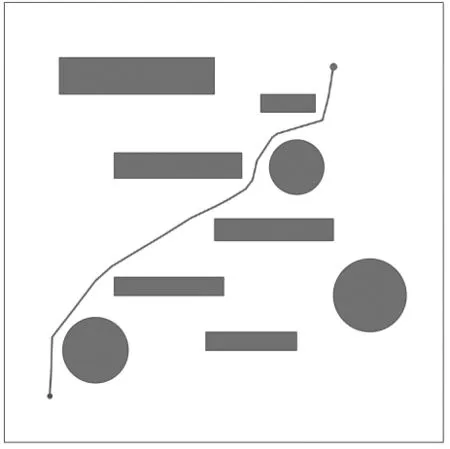
圖6 膨脹操作后的路徑圖Fig.6 Path map after expansion operation

取表3中每行兩點坐標形成連線，不考慮點(60.00，85.00)，計算兩點連線的斜率，并繪制成折線圖如圖7。

表3 路徑點坐標Table 3 Path point coordinates

由圖7可知，其波動較大，在機器人實際運行過程中，會表現為運行至折角處速度發生突變并快速轉向，不利于機器人在真實搬運環境下的平穩運行。

圖7 斜率變化折線圖Fig.7 Line chart of slope change

增加障礙物膨脹后的算法迭代過程如圖8，其橫坐標為時間，單位：秒（s），縱坐標為路徑代價。算法在0.09678s后成功尋找到最初路徑，并快速收斂，在2.037s后尋找到次優路徑，與最優路徑259.1的代價值相差僅為4，并最終在9.57s時收斂至最優。

圖8 增加障礙物膨脹后的迭代過程Fig.8 Iteration process after adding obstacle expansion

圖9為本文在圖6基礎上加入Bezier曲線優化后得到的路徑，其路徑代價值為258.88，與原先最優路徑相比，其代價值減少了0.22，路徑更加平滑，更適合機器人的平穩運行。

圖9 Bezier曲線優化后的路徑Fig.9 Optimized path of Bezier curve

仿真實驗結果表明，經過障礙物膨脹和曲線優化后的BIT算法在復雜環境和大場景范圍下仍能夠快速求解出路徑并迅速收斂，并能在減小路徑的代價值的同時使得機器人的運行更加平穩，能夠滿足農業大場景下的路徑規劃要求。