面向降載的漂浮式海上風機變槳距控制技術

陳殿輝, 徐曼如, 朱 政, 洪炫宇, 李建國

(1.上海電機學院 電氣學院, 上海 201306;2.國網(wǎng)上海奉賢供電公司, 上海 201400;3.三峽新能源海上風電運維江蘇有限公司 大豐項目部, 江蘇 鹽城 224008)

為順應新時代背景下“碳達峰、碳中和”的目標,我國能源結構將發(fā)生改變[1],新能源發(fā)電發(fā)展迅速,而風電逐步成為新能源發(fā)電的主力軍。近年來,陸上風電不斷開發(fā),陸上可利用風資源逐漸減少,擁有較好發(fā)展前景的海上風電已成為我國風電行業(yè)發(fā)展的重心[2]。2020年7月,我國首臺海上漂浮式風電平臺——“三峽引領”號在廣東陽江成功安裝,這表明我國海上風電開始向深海化發(fā)展[3]。

和近海(水深＜50 m)相比,深海(水深＞50 m)擁有更好的風資源,更利于發(fā)展海上風電。相較于在深海安裝固定式海上風機,漂浮式海上風機的成本更低,但面臨的載荷環(huán)境更復雜。目前,國內(nèi)外部分學者對風機獨立變槳距控制開展了相關研究。曹松青等[4]設計了一種非線性預測控制和PID 控制相結合的獨立變槳距控制技術,該獨立變槳距控制技術能有效解決系統(tǒng)的內(nèi)外擾動。曾凌霄等[5]基于600 k W 水平軸海流能風機設計了一種變槳系統(tǒng),該系統(tǒng)不僅保證了功率穩(wěn)定,還能顯著降低葉輪受到的不平衡載荷。閆學勤等[6]提出了一種基于科爾曼坐標變換的改進型準比例積分諧振獨立變槳距控制算法,該獨立變槳距控制算法對機組輸出的有功功率無沖擊影響。曾冰等[7]提出了一種基于鯨魚群算法的PID獨立變槳距參數(shù)整定方法,該方法能優(yōu)化控制器的參數(shù)。Gong等[8]將模糊PID和混沌算法結合,設計了一種獨立變槳控制器,研究發(fā)現(xiàn)該控制器的性能較好。周臘吾等[9]提出了一種基于徑向基函數(shù)神經(jīng)網(wǎng)絡的獨立變槳距控制技術,結果表明,該獨立變槳距控制技術能優(yōu)化漂浮式海上風機的發(fā)電功率。劉楊等[10]提出了一種基于改進微分進化算法的兆瓦級風機獨立變槳距控制技術,研究發(fā)現(xiàn)該獨立變槳距控制技術縮小了PID 參數(shù)的搜索范圍,有效穩(wěn)定了輸出功率。

目前,國內(nèi)外大多數(shù)學者對漂浮式海上風機降載的研究側重于通過優(yōu)化浮式平臺結構降低平臺受到的載荷,對獨立變槳距控制技術的研究側重于優(yōu)化陸上風機和海上固定式風機的發(fā)電功率,對獨立變槳距控制技術下漂浮式海上風機的平臺垂蕩運動和葉尖位移引起的載荷變化的相關研究較少。本文采用OpenFAST軟件對漂浮式海上風機系統(tǒng)建模,針對漂浮式海上風機面臨的復雜海況,提出一種基于卡爾曼濾波算法的改進單神經(jīng)元PI獨立變槳距控制技術。對比PI統(tǒng)一變槳距和方位角權系數(shù)獨立變槳距控制技術,分析了在本文提出的獨立變槳距控制技術下漂浮式海上風機的平臺垂蕩運動和葉尖位移的振幅變化。仿真結果表明:本文提出的獨立變槳距控制技術緩解了浮式平臺的垂蕩運動,減少了葉尖位移的振幅,在一定程度上降低了漂浮式海上風機受到的載荷。

1 氣動 水動 系泊系統(tǒng)模型

半潛式漂浮式海上風機由1個中央圓筒和3個浮筒構成,該類型漂浮式海上風機安裝難度較小[11]。漂浮式海上風機大多安裝在深海區(qū)域,面臨的載荷環(huán)境十分復雜,導致漂浮式海上風機的系統(tǒng)模型呈現(xiàn)強耦合的特點,漂浮式海上風機的系統(tǒng)動力學模型主要包括氣動、水動和系泊模型。圖1為半潛式漂浮式海上風機。

圖1 半潛式漂浮式海上風機

1.1 氣動模型

漂浮式海上風機平臺共有6個自由度運動,其中包括X、Y、Z3 個方向的平動自由度為縱蕩(Surge)、橫蕩(Sway)、垂蕩(Heave),以及3個轉動自由度為縱搖(Pitch)、橫搖(Roll)、艏搖(Yaw)。圖2為漂浮式海上風機平臺自由度運動。

1.1.1 氣動載荷(風輪) 漂浮式海上風機的氣動載荷主要源于風輪受到的軸向力和風輪轉矩[12],通過葉素 動量理論對漂浮式海上風機的葉片進行假設切割,分成足夠多的葉素。氣動載荷作用在葉素上產(chǎn)生使葉片轉動的推力T和扭矩M[13]:

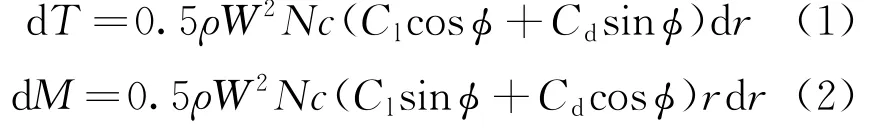
式中:ρ為來流密度;W為相對來流速度;N為葉片數(shù)目;c為葉素翼型弦長;Cl、Cd分別為翼型升力和阻力系數(shù);?為入流角;r為葉片半徑。

1.1.2 氣動載荷(塔筒) 漂浮式海上風機塔筒的氣動載荷為[14]

式中:K為平臺桿件形狀受力系數(shù);H為高度系數(shù);Sa為塔筒桿件a的受風面積;vt為塔筒處的相對風速。

1.2 水動模型

1.2.1 水動載荷(海流) 在海洋工程中,一般將深海區(qū)域的海流速度視為線性變化,漂浮式海上風機受到的海流力為

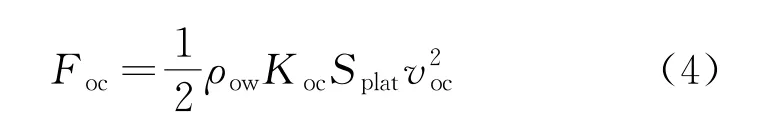
式中:ρow 為海水密度;Koc為曳力系數(shù);Splat為平臺和海流垂面的投影面積;voc為海流流速。

1.2.2 水動載荷(波浪) 在海洋工程中,常采用莫里森(Morison)方程計算浪載荷[15]。漂浮式海上風機受到的波浪力Fwa為拖曳力Ft和慣性力Fg之和,拖曳力和慣性力的表達式為

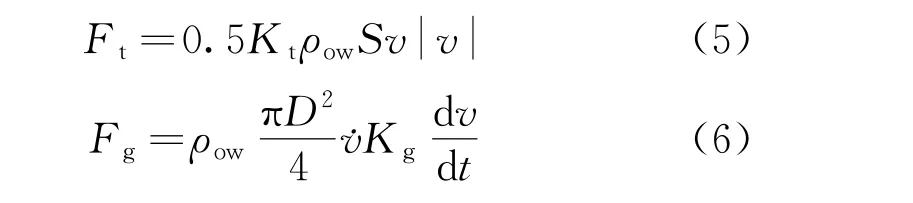
式中:Kt為拖曳力系數(shù);S為浮筒垂于海水流動方向的投影面積;v為海水的瞬時流速;D為構件直徑;?v為流體瞬時加速度的水平分量;Kg為慣性力系數(shù)。

1.3 系泊系統(tǒng)模型

通常采用靜態(tài)懸鏈線方程計算漂浮式海上風機系泊系統(tǒng)的系泊力,該方程中系泊點處的系泊力水平分量Fxs和垂直分量Fxc分別表示為[16]式中:X為懸鏈線水平跨距;l為系泊纜長度;h為錨點和系泊點間的垂直距離;ω為水中單位長度系泊纜的重力。

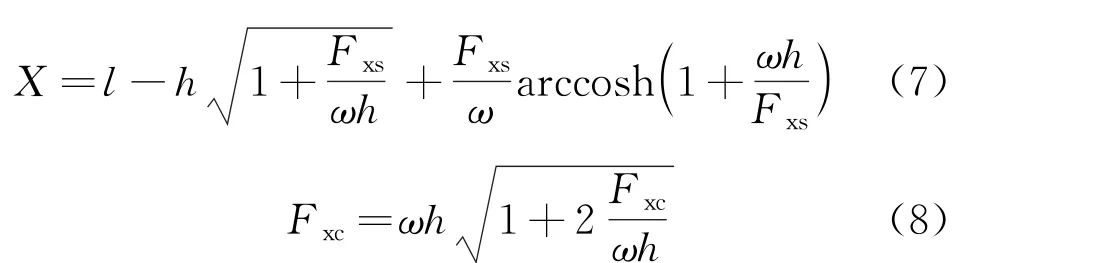
1.4 漂浮式海上風機運動方程

結合漂浮式海上風機的氣動、水動和系泊系統(tǒng),其運動方程[17]如下:

2 變槳控制器設計

2.1 統(tǒng)一變槳控制(Collective Pitch Control,CPC)

本文的CPC采用增益調度型PI控制,利用發(fā)電機實際轉速和額定轉速的轉速差作為輸入。該統(tǒng)一變槳距控制技術能在PI控制需要較大葉片槳距角時給出較小的增益,即增益同葉片槳距角的變化量成反比[18],其傳遞函數(shù)為[19]

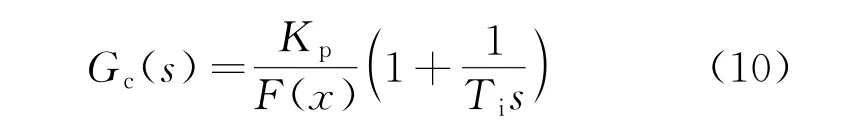
式中:Kp為比例系數(shù);F(x)為增益因子;Ti為積分時間;s為拉氏變換算子。

2.2 獨立變槳控制(Individual Pitch Control,IPC)

A) 受環(huán)境載荷和葉輪面積較大等因素影響,漂浮式海上風機3個葉片受到的載荷差異較大。該控制技術根據(jù)每個葉片的受力情況進行權系數(shù)的修正,忽略葉片間的結構差異,將每只葉片中心點位置的風速等效為平均風速,經(jīng)推導得到權系數(shù)為

2.2.1 方位角權系數(shù)控制技術(IPC

2.2.2 基于卡爾曼濾波算法的改進單神經(jīng)元PI控制技術(IPC B)

(1) 卡爾曼濾波算法。鑒于漂浮式海上風機受環(huán)境載荷影響較大,輸出常含有干擾信號。基于卡爾曼濾波算法,旨在從干擾信號中確定有效信號。該算法利用狀態(tài)方程描述系統(tǒng),由上段時間的估值和現(xiàn)在的觀測值遞推得到現(xiàn)在的狀態(tài)估值為[20]

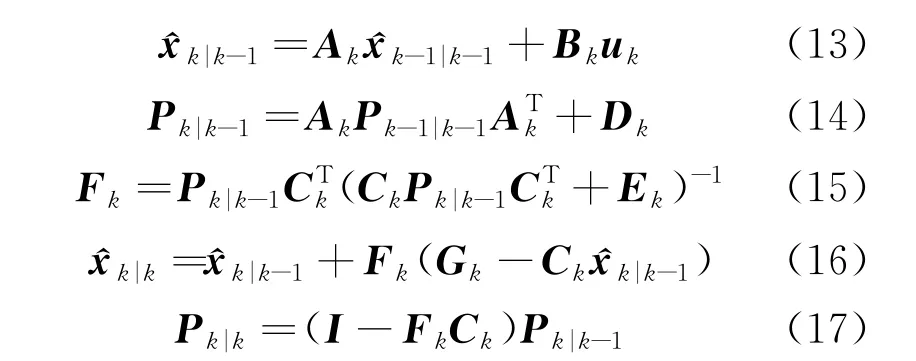
式中:x^k|k-1為k時刻的先驗狀態(tài)估計值;Ak、Bk、Ck均為變換矩陣;uk為控制向量;Pk|k-1為協(xié)方差矩陣;Dk為過程噪聲的協(xié)方差矩陣;Fk為濾波增益矩陣;Ek為觀測噪聲的協(xié)方差矩陣;x^k|k為k時刻的后驗狀態(tài)估計值;Gk為測量值;I為單位矩陣。

(2) 改進單神經(jīng)元PI控制。單神經(jīng)元PI控制具有結構簡單、自主學習和魯棒性強等優(yōu)點。但考慮到單神經(jīng)元PI控制受e(k)和Δe(k)影響較大,本文對常規(guī)單神經(jīng)元PI控制的學習規(guī)則進行改進:用e(k)+Δe(k)代替常規(guī)單神經(jīng)元PI控制器中xi(k)[21]。

改進后的學習規(guī)則如下:

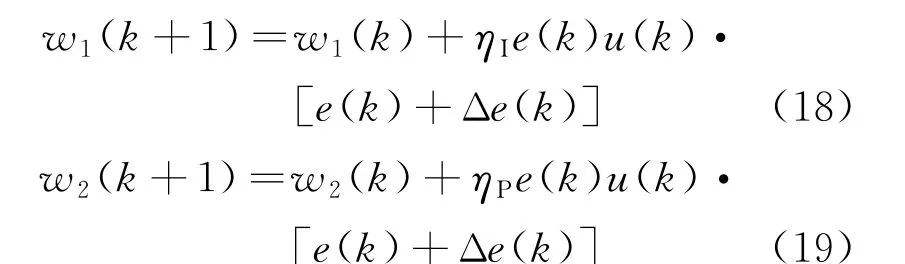
式中:w1(k)、w2(k)分別為第1和第2個神經(jīng)元的連接權值;ηP、ηI 分別為比例控制和積分控制的學習速率;e(k)為k時刻的誤差值;u(k)為k時刻的控制量;Δe(k)為k時刻的誤差變化量。

3 仿真分析

本文以NREL-5 MW基礎風機和OC4-DeepCwind漂浮式平臺為研究對象,通過OpenFAST 和Matlab/Simulink聯(lián)立仿真。仿真時間為200 s,設定平均風速為17 m/s的湍流風、有義波高為4 m的不規(guī)則波聯(lián)合作用的運行工況。鑒于切入風速較大,本文取前100 s為瞬態(tài)部分,僅分析100～200 s的仿真結果。NREL-5 MW 風力機主要參數(shù)如表1所示,OC4-DeepCwind漂浮式風力機平臺主要參數(shù)如表2所示。

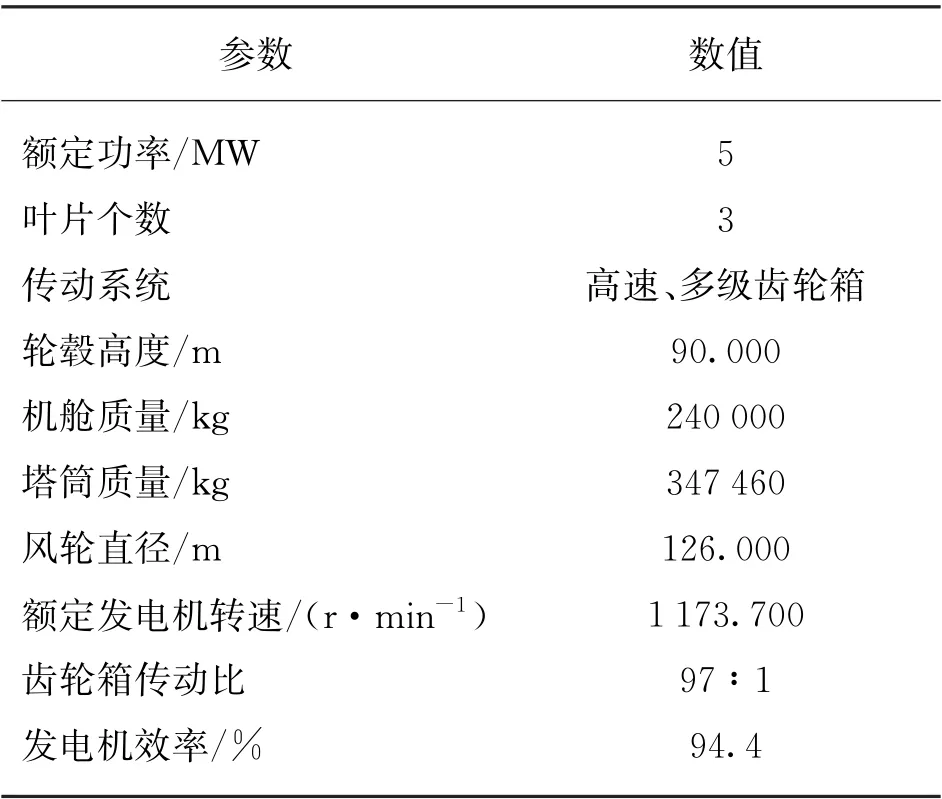
表1 NREL-5 MW 風力機主要參數(shù)

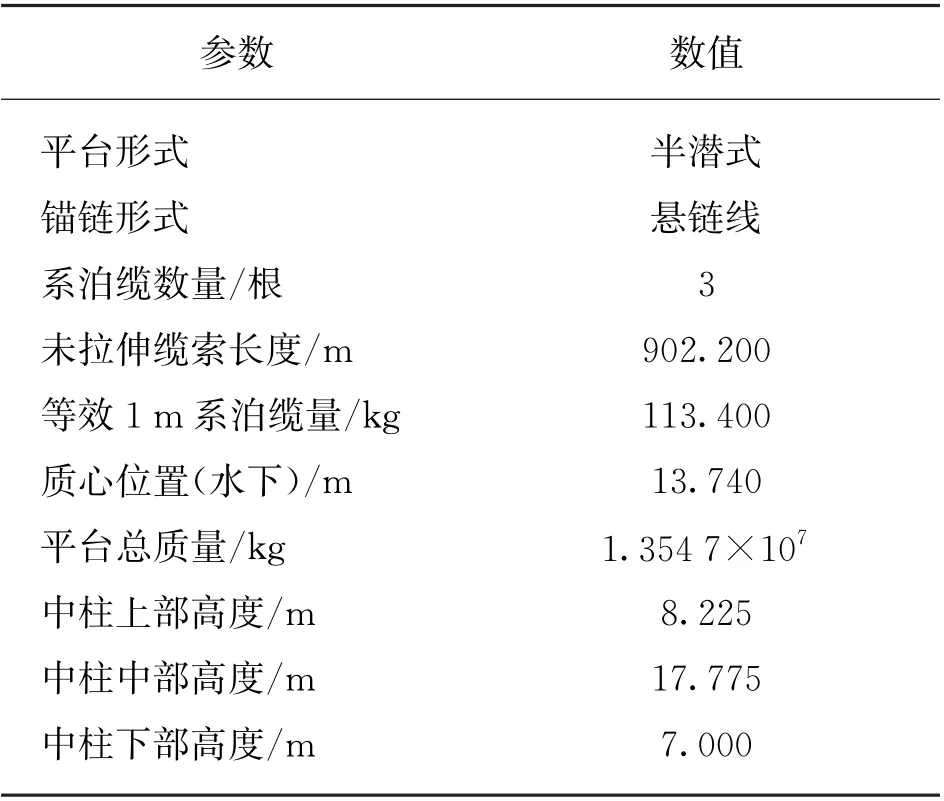
表2 OC4-DeepCwind漂浮式風力機平臺主要參數(shù)

圖3反映了設定的風機運行工況。由圖3(a)可知,在0～200 s內(nèi),風速最大值和最小值分別為23.99 m/s和8.49 m/s;在100～200 s內(nèi),風速最大值和最小值分別為23.99 m/s和10.78 m/s,均處于機組切入、切出風速以內(nèi)。生成的湍流風振蕩明顯,最大幅值達到13.21 m/s,一定程度上反映了湍流風對機組可靠性要求較高。由圖3(b)可知,生成的不規(guī)則波浪振蕩明顯,一定程度上反映了浪載荷對浮式平臺的可靠性要求較高。

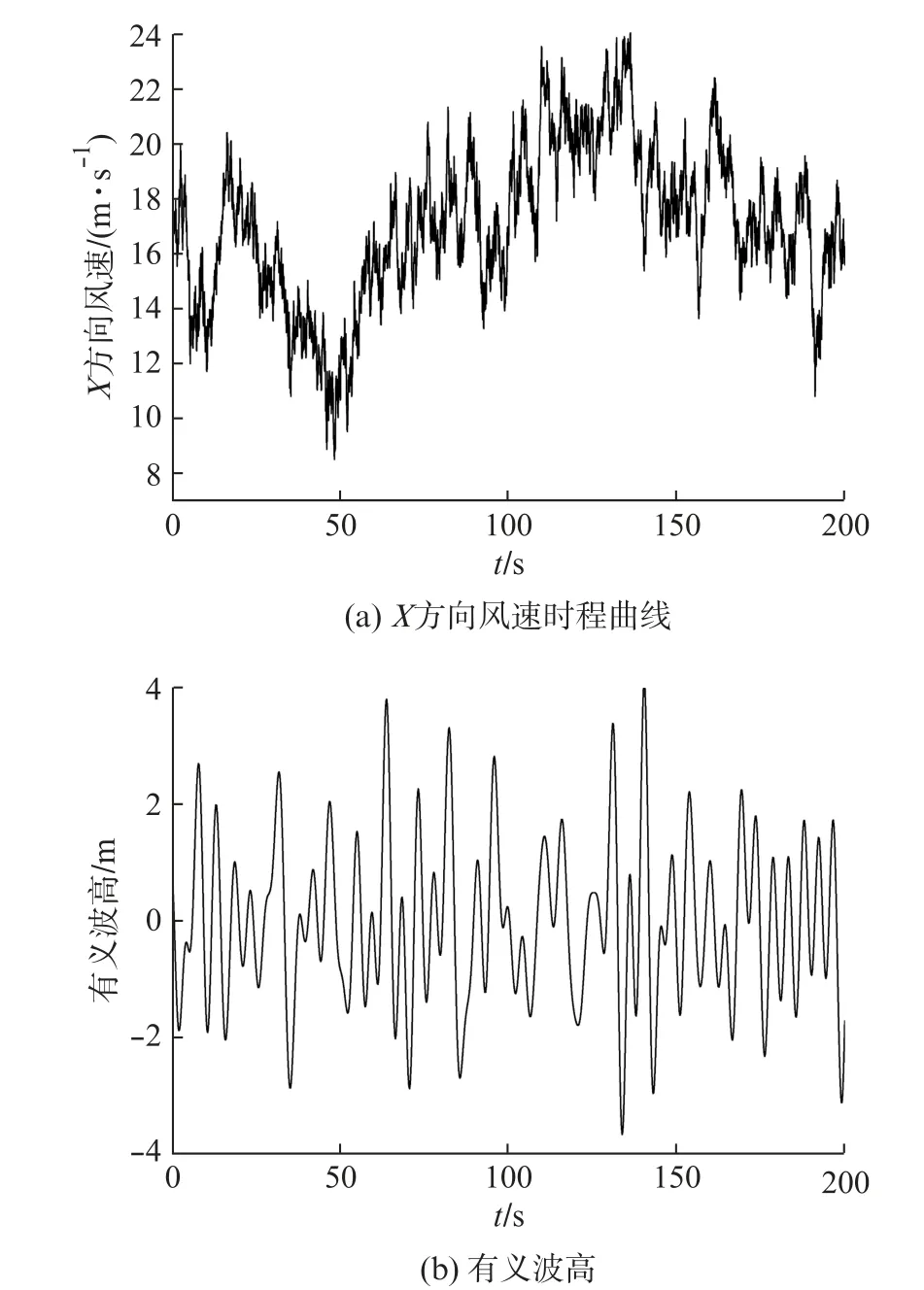
圖3 風機運行工況

結合圖4平臺載荷分析對比和表3標準差分析可知,在湍流風、不規(guī)則波浪聯(lián)合作用下,對比本文中的CPC和IPC A,IPC B下的平臺垂蕩運動的標準差分別下降了9.9%和10.6%,表明IPC B能緩解平臺垂蕩運動,使平臺更穩(wěn)定,在一定程度上降低了由平臺運動引起的載荷。此外,葉片1葉尖位移的振幅在IPC B 下也更小,對比本文中的CPC和IPC A,IPC B下的葉片1葉尖位移的標準差分別下降了23.4%和3.09%,葉片1葉尖位移的振幅減小反映出在IPC B下葉片擺動范圍減小,葉片擺動范圍減小能緩解機組晃動,從而降低葉片載荷和機組受到的載荷。

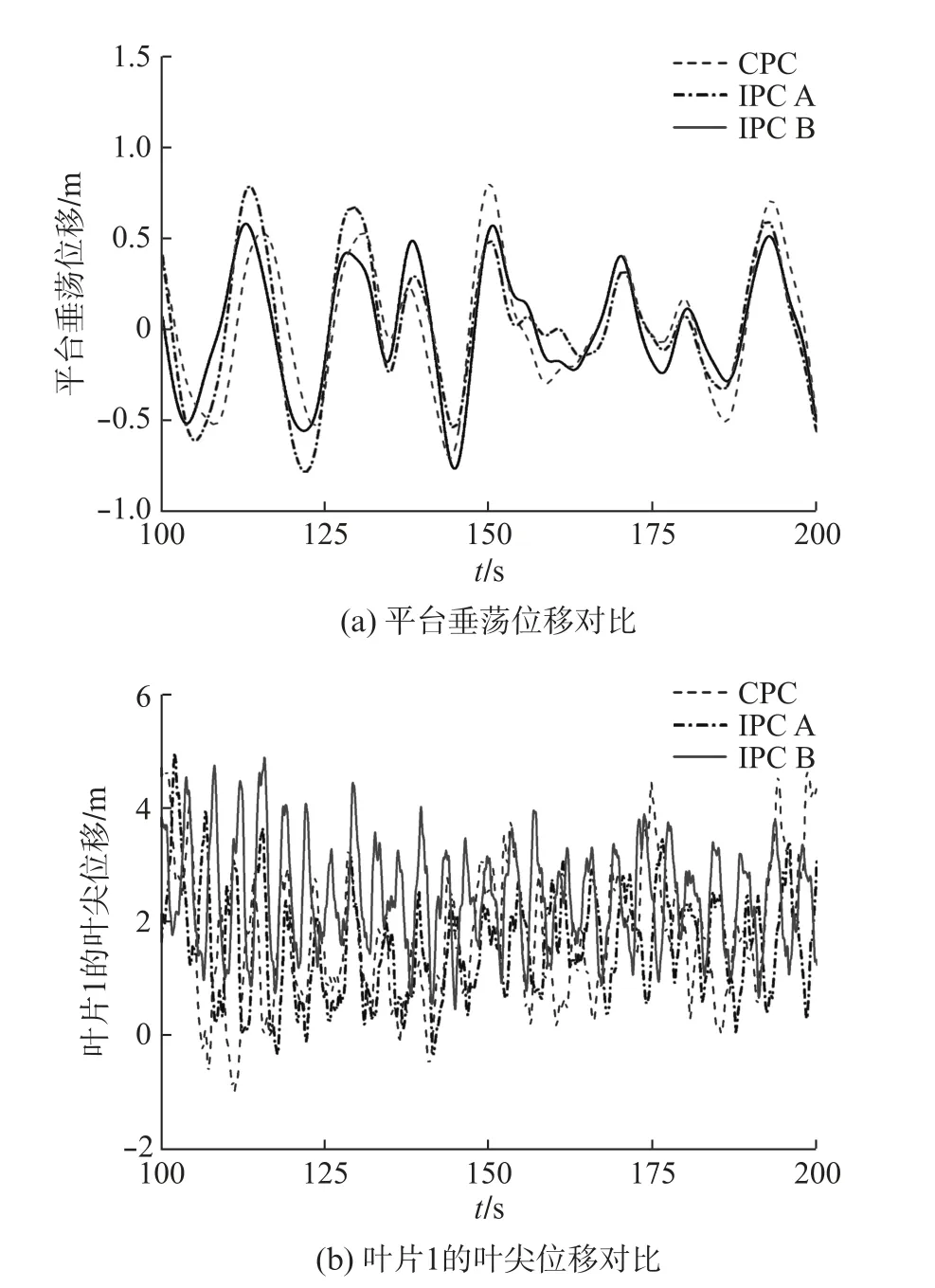
圖4 平臺載荷分析對比

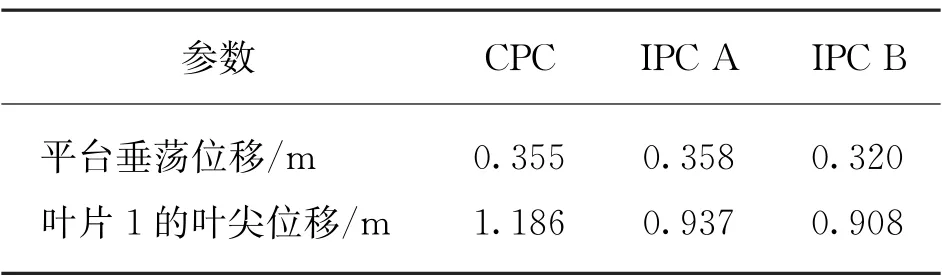
表3 3種變槳距控制技術標準差分析

4 結 論

對比3種不同變槳距控制技術,分析半潛式漂浮式海上風機受到載荷變化后得出以下結論:

(1) 在緩解漂浮式海上風機的平臺垂蕩運動和降低葉片1葉尖位移方面,IPC B優(yōu)于CPC和IPC A。在IPC B下,平臺垂蕩位移減小,一定程度上緩解了浮式平臺的晃動,降低了漂浮式海上風機由平臺運動引起的載荷。

(2) 在IPC B 下,葉片1葉尖位移的振幅減小,在一定程度上能減小由葉片擺動引起的載荷,延長葉片的壽命。