基于直線特征的合作目標加權位姿估計*

邢亞斌 王汝童 譚振國 郭永奇 于 濤

（北京化工大學信息科學與技術學院 北京 100029）

1 引言

隨著我國高端制造業的快速發展，迫切需要對大型構件的三維幾何參量進行高精度測量，以確保裝配精度。當使用三維測量儀器對裝配在大型構件表面的合作目標進行瞄準時，大型構件所處外界環境會影響合作目標的成像質量，導致其位姿估計精度較低，從而使測量精度降低。因此，研究合作目標加權位姿估計方法，減少外界環境造成的干擾，對提高合作目標位姿估計的精度具有重要意義和應用價值。

合作目標具有較為簡單、明顯的幾何特征，且在3D世界坐標系中的坐標精確已知，有利于建立2D圖像特征與3D合作目標之間的對應關系，位姿估計的復雜度低［1］。合作目標位姿估計方法主要可以分為基于n點透視模型（Perspective-n-Point，PnP）［2］和基于n線透視模型（Perspective-n-Line，PnL）［3］的方法。相比于點特征，直線特征所包含的屬性更為豐富，而且提取較為穩定，受噪聲的影響較小，可靠性高［4］，因此PnL問題受到了更為廣泛的關注和研究。

根據PnL模型求解方法的不同，可分為非迭代方法和迭代方法［5］。其中非迭代方法主要有Mirzaei等［6］提出的全局最優線性求解方法，該方法將優化問題轉化為對三個三次方程組的求解問題，簡化了優化過程，但是由于麥考利矩陣的構建緩慢，總計算時間仍然較高；Zhang等［7］提出的RPnL方法，采用構建局部坐標系間接求取目標位姿的方法，簡化了計算過程，其時間復雜度為O()n，位姿解算效率高，有效解決了直線共面情況下的位姿估計問題，能夠得到較為準確的目標位姿初值。雖然非迭代方法的位姿解算速度較快，但是對直線特征提取的精度要求較高［8］。當合作目標圖像受到測量環境影響發生質量退化時，會導致特征提取精度下降，非迭代方法的精度與穩定性都會受到較大影響［9］。

迭代法通過迭代的方式最小化特定的目標函數［10］，從而完成對位姿估計結果的優化，提高位姿估計精度［11］。此類方法能夠通過準確的初值和層層的迭代提高位姿估計精度［12］。但是由于其迭代優化方法多為無差別優化［13］，并不能有效地解決由圖像質量退化問題造成的直線定位偏差為位姿估計精度帶來的影響［14～15］。張躍強等［16］提出的基于直線間積分距離度量的位姿估計方法屬于無差別優化方法，認為每一條直線估計出的結果對誤差的貢獻相同來優化目標函數，會加大提取的相對不準確的直線對位姿估計結果的影響。針對該問題，張振杰等［17］為提高位姿估計的抗噪性，對每條直線進行加權，該方法假設權值服從高斯分布，并對其進行迭代優化，但是該權值具有一定隨機性，并不能準確表示每條直線提取的精度。

本文在現有的PnL位姿估計方法的基礎上，針對大型構件所處環境對合作目標圖像成像質量造成的影響，在位姿估計過程中引入了直線端點特征的約束，提出了一種合作目標加權位姿估計方法。該方法根據直接提取的直線端點與其對應的通過幾何約束關系計算的直線端點的距離賦予每條直線權值，在位姿優化過程中，根據每條直線的權值對其重投影誤差進行加權，提高合作目標位姿估計的準確性，并保持較快的位姿估計速度。

2 基于直線特征的合作目標加權位姿估計

2.1 RPnL位姿估計方法

合作目標中普遍存在直線特征，采用RPnL方法［7］可以對其位姿初值進行求解，位姿估計的主要原理如下。

首先構建局部坐標系Om-XmYmZm，選擇圖像中具有最長投影直線長度的參考直線L0作為Zm軸，Xm軸為參考直線L0與相機光心Oc構成的投影平面Π的法向量n0，則Ym軸也可確定。世界坐標系Ow-XwYwZw旋轉到Om-XmYmZm的旋轉矩陣Rmw，可由V w0與V m0確定。其坐標系轉換關系如圖1所示。

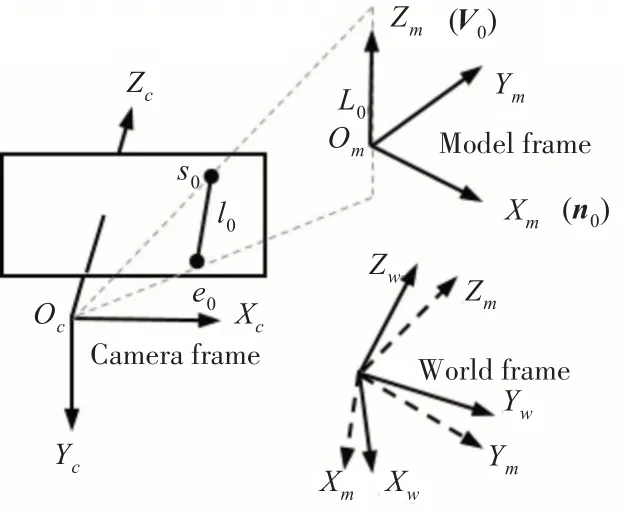
圖1 坐標系轉換關系

另外選擇圖像中具有第二長投影直線長度的參考直線L1為輔助線，將線組{Li}分為n-2個三元組{L0L1Lj|j=2…n-2}，根 據 相 機 坐 標 系Oc-XcYcZc下直線li方向向量Vic垂直于法向量ni可得約束函數

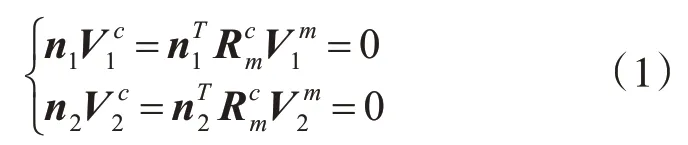
式 中，Rcm=R′Rot(Xm，α)Rot(Zm，β)表 示 由Om-XmYmZm旋轉到Oc-XcYcZc的旋轉矩陣；R′為以n0為首列的隨機正交旋轉矩陣。由式（1）可得

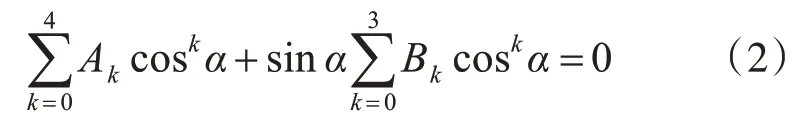
式中，系數Ak、Bk可由計算得到。將sin2α=1-cos2α代入式（2），并令x=cosα可得

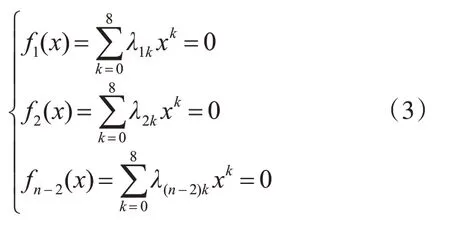
式中，系數λk可由n1、n2、V1m、V2m計算得到。

使用最小二乘殘差法來求取系統的局部最小值可解得繞Xm軸旋轉的角度α，則Rcm可簡化為式中=R′Rot(Xm，α)，根據直線透視投影關系可得

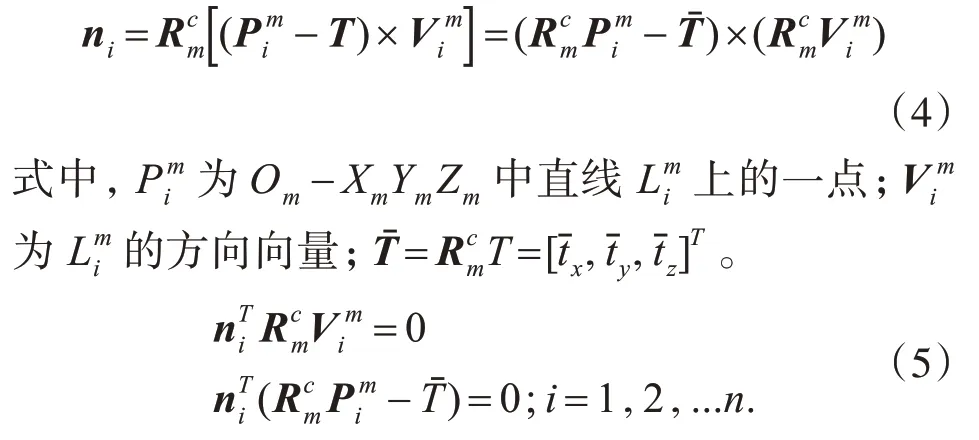
根據式（5），對于n條直線，可以得到2n個參數向量為[cosβ，sinβ，，1]T的齊次線性方程組如下所示：

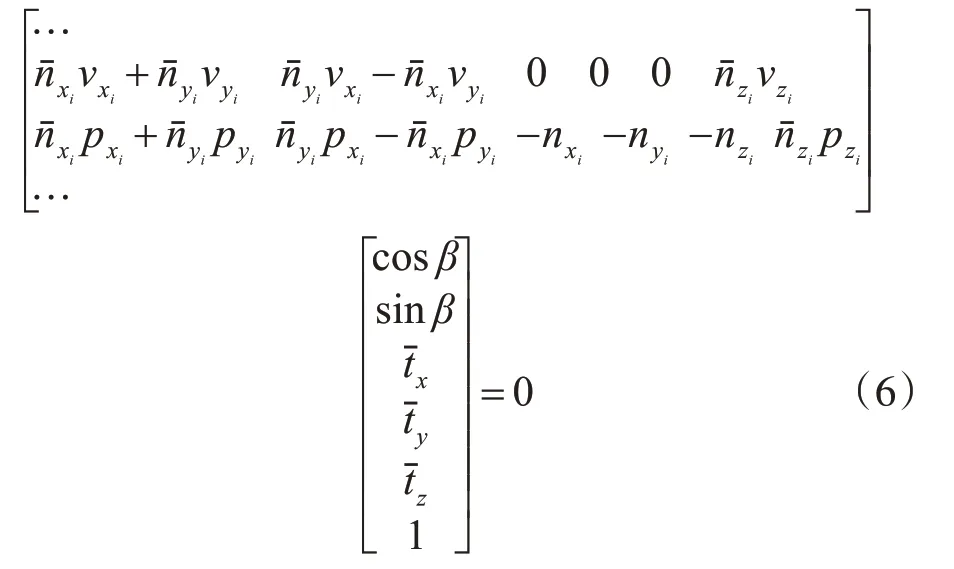
通過對齊次方程組進行SVD分解可以求出β和，從而可以計算出平移向量T=，最后可得到由Ow-XwYwZw旋轉到Oc-XcYcZc的旋轉矩陣=，即可求得目標對應的位姿參數矩陣M。

RPnL位姿估計方法對合作目標位姿初值進行了線性求解，但是該方法未經迭代優化，位姿估計精度有限，且易受干擾。

2.2 基于直線特征的合作目標加權位姿估計方法

采用RPnL方法獲得合作目標的位姿初值之后，通過迭代方法對直線重投影誤差進行優化，可以獲得最優的位姿參數矩陣M。

本文所采用的合作目標為方形靶標（單個網格尺寸為62.5mm×62.5mm）和圓形靶標（內刻圓形直徑為125mm），方形靶標中同時存在點、線幾何特征，圓形靶標中同時存在點、線、圓幾何特征，通過特征提取方法直接提取點特征，可以獲得各直線的端點坐標；通過直線之間或直線與圓之間的幾何約束關系，可以計算得到直線端點坐標。計算直接提取的直線端點到利用幾何約束關系計算的對應直線端點的距離，可以確定直線特征提取的置信度。提取的直線和提取的點越接近則認為直線提取的置信度越高，所以在位姿估計的優化過程中，該條直線對應的權重大；而對于直線和點距離誤差較大的情況，說明這部分提取的不好，那么則需抑制這部分對最終結果的影響，減少它的權重。

假設合作目標中有m條模型直線，表示為{L1，L2，…Li，…Lm}，直線的重投影距離可表示為模型直線Li的端點到投影平面Π的距離［16］，如圖2所示。

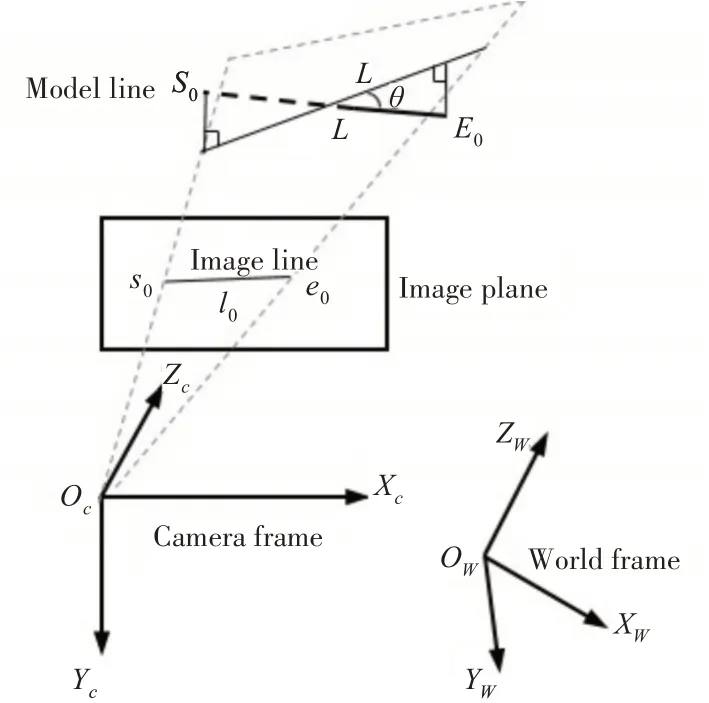
圖2 模型直線段端點到投影平面的距離

合作目標圖像中的直線方程用極坐標表示為

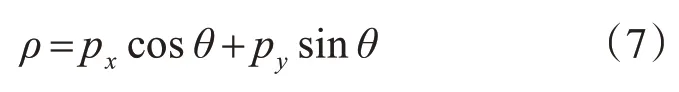
將圖像直線端點坐標代入式（7）可得

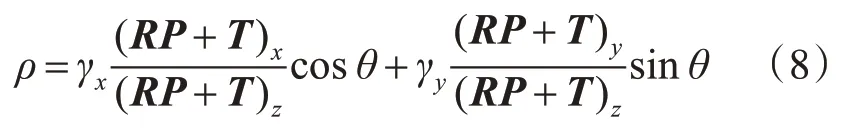
式中，γx、γy分別表示相機焦距與x軸、y軸方向像元尺寸的比值；式（8）可以簡化為

式中，n0=(γxcosθ，γysinθ，-ρ)T，其單位法向量可以表示為，則L在Π上的約束為

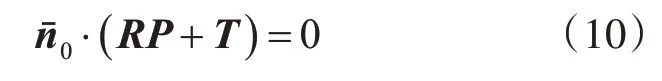
則L的端點到Π的距離為

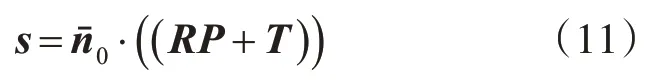
以最小化該距離為目標構建誤差函數如下

采用引入直線權值的方法對誤差函數進行改進，計算提取的直線端點到利用幾何約束關系獲得的端點的距離di，可確定直線權值，如下式所示。

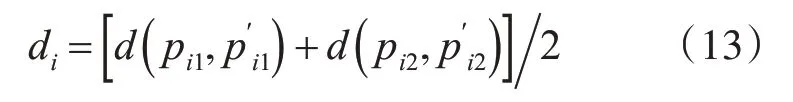
式中，(pi1，pi2)為圖像中直接提取得到的直線端點坐標；()為利用幾何約束關系計算得到的對應直線端點坐標。di越大則說明該條直線的提取置信度越低，則對應的權值越小。將di取倒數后歸一化作為權值ωi，可得

則引入權值后的直線重投影誤差優化的誤差函數為

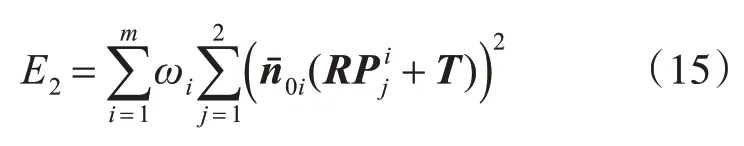
通過對其進行迭代求解，可得到最優的直線重投影誤差，從而求解出對應的合作目標位姿參數矩陣M。

在合作目標的實際成像過程中，由于測量環境的影響會導致被測合作目標圖像中可能存在噪聲、模糊、光照變化等多種影響直線特征提取的干擾因素，而直線特征提取的精度會直接影響到基于直線特征的位姿估計的精度。所提合作目標加權位姿估計方法在優化重投影誤差的過程中采用加權的方式引入每條直線的權值，可以提高合作目標位姿估計的準確性。

2.3 基于直線特征的合作目標加權位姿估計算法流程

本文提出的基于直線特征的合作目標加權位姿估計算法流程如圖3所示，實現步驟如下。

圖3 合作目標加權位姿估計算法流程框圖

步驟1輸入合作目標圖像，相機內參數矩陣及畸變系數，設置最大迭代次數與誤差閾值ε*。

步驟2提取合作目標圖像中的幾何特征，根據幾何約束關系獲取直線端點坐標，計算其與直接提取的對應直線端點的距離di，并將di的倒數歸一化作為權值ωi。

步驟3構建局部坐標系，將每3條直線分為一組，計算由局部坐標系到相機坐標系的旋轉矩陣Rcm，進而確定由世界坐標系到相機坐標系的旋轉矩陣Rcw和平移向量T。

步驟4引入權值ωi構造新的直線重投影誤差優化的誤差函數E2。

步驟5將位姿初值代入目標函數，判斷計算結果是否小于誤差閾值ε*，若不滿足，則繼續迭代。

步驟6輸出優化后的位姿參數。

3 實驗與分析

實驗所用圖像為相機在真實環境下拍攝得到的多幅方形靶標圖像（單個網格尺寸為62.5mm×62.5mm）和圓形靶標圖像（內刻圓形直徑為125mm），圖像尺寸為3024×4032像素。對比實驗為文獻［7］的位姿估計方法。

實驗采用重投影特征點平均距離誤差與位姿估計時間作為位姿估計結果的質量評價指標，其中重投影特征點平均距離誤差的計算公式為

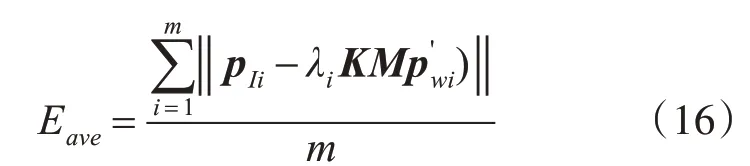
式中，pIi表示原2D特征點的坐標；表示3D特征點的坐標；M表示位姿參數；m表示特征點數量；λi表示任意的比例系數。

使用本文方法分別對3幅實拍的方形靶標圖像與圓形靶標圖像進行位姿估計處理，將所得到的位姿估計結果與文獻［7］方法的結果進行對比，驗證方法的有效性，圖4為實驗所用的合作目標圖像。

圖4 合作目標圖像

合作目標圖像的位姿估計結果如表1所示，對比位姿估計結果可以看出，本文位姿估計方法較文獻［7］方法的精度有所提高，位姿估計時間與其相當。3幅方形靶標圖像重投影特征點平均距離誤差的平均值為4.9798pixel，位姿估計時間的平均值為0.193s；與文獻［7］方法相比，重投影特征點平均距離誤差的平均值減小0.3253pixel，位姿估計精度提高6.13%。3幅圓形靶標圖像重投影特征點平均距離誤差的平均值為3.4317pixel，位姿估計時間的平均值為0.189s；與文獻［7］方法相比，重投影特征點平均距離誤差的平均值減小0.3719pixel，位姿估計精度提高9.78%。

表1 合作目標圖像位姿估計實驗結果

通過對比實驗所得到的位姿估計結果可以得出，本文方法的位姿估計精度在總體上優于文獻［7］方法，能夠提高合作目標的位姿估計精度，并保持較快的位姿估計速度。

4 結語

為了提高合作目標的位姿估計精度，實現三維測量儀器對合作目標的高精度瞄準，提出了一種基于直線特征的合作目標加權位姿估計方法。首先提取圖像中的合作目標關鍵幾何特征，通過幾何約束關系獲取各直線端點；然后計算其與直接提取的對應直線端點的距離，將距離的倒數歸一化作為權值；最后將所得權值引入直線重投影誤差的計算過程中構建新的誤差函數，完成對合作目標位姿參數的優化。實驗結果表明，所提方法的位姿估計精度優于文獻［7］方法，方形靶標的位姿估計精度提高6.13%，圓形靶標的位姿估計精度提高9.78%，位姿估計時間與其相當，能夠有效減小外界環境對位姿估計結果帶來的影響，提高合作目標的位姿估計精度。