基于光譜共焦的電路板微型元器件三維高精度檢測*

張志榮 洪漢玉 章秀華

（1.武漢工程大學光學信息與模式識別湖北省重點實驗室 武漢 430205）（2.武漢工程大學湖北省視頻圖像與高清投影工程技術研究中心 武漢 430205）（3.武漢工程大學電氣信息學院 武漢 430205）

1 引言

在現代化生產和國防技術推動下，現代制造業的自動化程度越來越高，產品質量檢測作為制造業中至關重要的環節也在不斷發展，如何提高產品檢測的精度和效率成為制造業發展的關鍵問題［1］。電路板作為現代制造業中最基本的電子部件，為各種不同大小、不同功能的元器件提供電路連接，是非常重要的載體［2］，電路板上任何一個元器件尺寸不合格都會影響電路板與其他機械部件的契合度，導致整體產品裝配不成功［3］。傳統的電路板檢測主要通過專業人員肉眼檢測，勞動強度大，效率低，不能滿足現代電路板批量生產和質量達標的需求［4］。近年來出現的現代化尺寸測量技術，如結構光測量技術［5］，硬件成本低、設備小巧，在一定范圍內測量精度較高；還有激光三角測量技術［6］，檢測速度快，最小精度可達100μm。但這些檢測方法的精度還是無法滿足精密電子產品行業高精度測量的要求。針對這些問題，本文提出采用非接觸、高精度、亞微米級光譜共焦傳感器的檢測方法實現對電路板元件高精度三維檢測［7］。

對電路板元件進行三維檢測過程中，需要通過采集的電路板元件空間點云獲取元件三維數據，而由于光譜共焦傳感器光源強度分布不均勻、各波長響應程度不同、系統噪聲等自身因素的影響［8］，采集的目標點云數據在空間中是零散分布的，特別是元件邊緣區域的點云數據穩定性低，部分噪聲點無法消除，所以必須對元件表面點云進行空間平面擬合來增加計算結果的準確性。最小二乘法根據兩個參數求解另一個參數的估值，完成擬合參數計算，該方法只考慮到觀測向量中的誤差，忽略了系數矩陣的誤差［9］；特征值法通過設置一個質量標準，在很大程度上優化平面參數的解法，但其無法消除噪聲對擬合過程中的干擾［10］；整體最小二乘法可以同時顧及觀測向量和系數矩陣的誤差，但由于異常點的影響，擬合效果也不是很好［11］。這些擬合方法將點云中的異常點和正常點賦予相等權重進行擬合，因此會影響最終檢測結果的精確度。

針對上述空間點云擬合影響測量精度的問題，本文提出一種基于自適應高斯權重空間點云平面擬合方法。該方法在空間點云平面擬合過程中，對點云邊緣區域和內部區域分配不同的擬合權值，可以減小邊緣區域雜質點對數據擬合精度的影響，提高檢測精度，實現對電路板元件的高精度三維檢測。

2 電路板點云數據獲取

2.1 光譜共焦傳感器原理

白光由許多單色光組成，光在不同介質中傳播時會產生單色光的折射。不同單色光在透鏡中的折射率是不同的，根據其波長范圍，短波在透鏡中折射率大，長波在透鏡中折射率小，在同一透鏡中，不同波長的單色光根據波長由短到長，焦點由近到遠地排列在光軸上，這樣成像就產生位置色差［12～13］。因為不同的單色光折射率不同所以經過透鏡成像也就不同，這是位置色差的形成原理。根據高斯公式將其表達為

式（1）中，l表示物距，r′是在透鏡折射下單色光形成的像距，f表示焦距。

位置色差會讓成像變得模糊，光譜共焦位移測量技術就是利用這一點來構建位移和波長的編碼，即彩色編碼［14］。當白光光源透過針孔時，由于位置色差不同色光就會分開，被測物體在可測范圍內通過光焦系統和共焦小孔不斷反射折射，最后形成不一樣的彩色光譜并與位移一一對應，從而可以得到波長和位移的關系，最后通過計算出射信號的峰值波長就可以得到物體位移［15］。光譜共焦傳感器的原理如圖1所示。

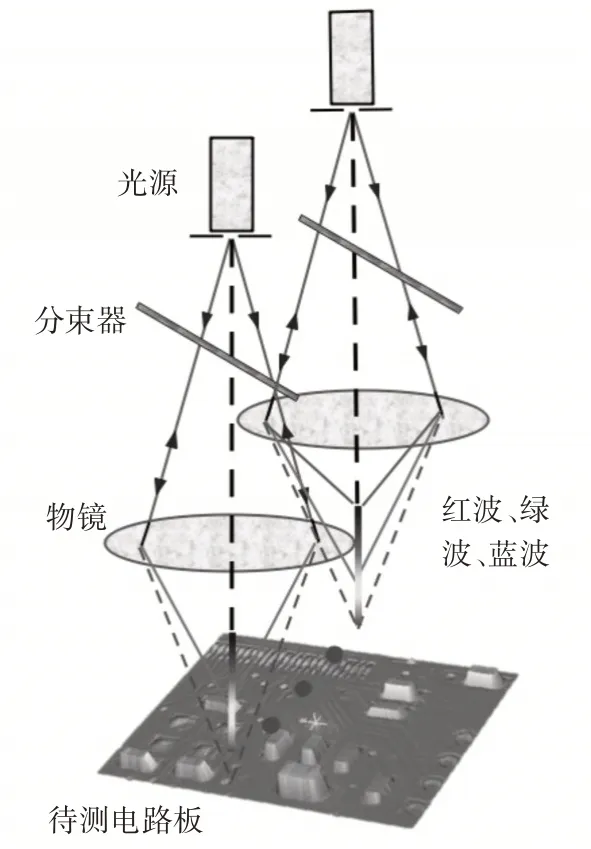
圖1 光譜共焦傳感器工作原理示意圖

2.2 基于光譜共焦的電路板3D點云數據采集

本文檢測系統主要由光譜共焦傳感器及信號處理系統、三坐標精密位移軸、計算機等部分組成，如圖2所示。三坐標位移軸精度高，空間定位能力強，驅動光譜共焦傳感器進行測量。

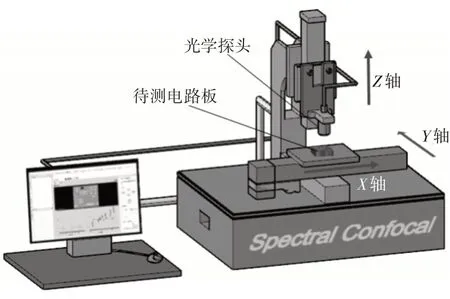
圖2 檢測系統結構示意圖

進行實驗測量時，首先將光譜共焦傳感器設置為測量距離模式，共焦探頭垂直安裝在X軸正上方。將電路板放置到XOY平面上，通過移動Z軸找到一個最適宜傳感器聚焦的位置，一般是光斑在物體上顯示為一個很亮的白點，這樣可以最大程度減小共焦系統由于自身因素產生的誤差。Z軸位置固定好后，通過計算機控制X軸、Y軸移動到采集的起始位置，記錄該位置的坐標信息，然后繼續移動X軸、Y軸到采集的終點位置并記錄其坐標信息。這樣采集開始時，X軸和Y軸會從起點位置交替運動，呈“弓”字型采集數據，直到運動到終點，采集完成。在軸運動期間，傳感器始終保持采樣，傳感器每經過一個位置都會以500Hz的頻率在該位置產生幾百甚至幾千個點，通過函數獲取這些點的值（相當于是z值），計算每個點z坐標的平均值最終以一個位置一個值的形式反饋到系統中，然后將其存儲在事先定義好的容器中；同時，通過坐標函數從精密位移軸獲取這些點對應位置的x值、y值，這樣將獲取的點以空間坐標的形式存儲起來形成點云，采集出物體的大致形狀，進而對其進行數據分析。本文通過光譜共焦系統采集點云數據，利用3D點云處理技術，對電路板元件進行高精度檢測。

3 點云數據處理及參數測量

3.1 點云數據預處理

采集得到的目標點云如圖3（a）所示，噪聲點在空間中分布稀疏、不均勻，本文先通過半徑濾波［16］將這些偏離主體點云的噪聲點剔除，圖3（b）是濾波后的結果。在空間分布上，每個目標點云部分之間具有獨立性，得到濾波處理的目標點云后，為求取高度等信息，需要將每個目標的上、下表面單獨分割出來，利用歐氏聚類點云分割算法將小于距離閾值的點劃分一個簇［17］。歐氏距離d用下式計算：

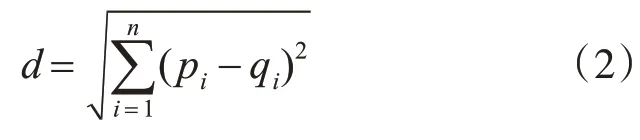
式中，pi，qi∈P，P是一個點云集合，如圖3（b）所示。P由圖3（b）中Q1、Q2、Q3組成，pi是分割前隨機設定的一點，qi是用KD-Tree［18］搜索到k個點中的一個點。該算法的具體實現步驟如下：

Step1：對于集合P中的一點pi，建立KD-Tree數據結構進行k近鄰搜索。

Step2：計算k個點到pi點的歐氏距離d，如果小于設定的距離閾值，將其聚類于Qi。

Step3：當Qi中有新的點進來之后，Qi類選取pi點之外的點繼續進行k近鄰搜索，重復一、二步；當Qi類中不再有新的點加入時，本次聚類結束。

圖3是用該算法對電路板元件點云進行聚類分割的結果，對該點云生成三個聚類Q1、Q2、Q3，即圖3（c）、（d）、（e）。

圖3 電路板元件點云分割圖

3.2 基于自適應高斯權重的點云平面擬合

本文通過空間點云平面擬合方法對電路板元件點云上下表面做擬合，擬合結果可以提高元件的3D檢測精度。現有的擬合方法如隨機采樣一致性擬 合（Random Sampling Consistency Fitting，RANSAC）、最小二乘擬合（Least Squares Fitting，LS）將全部數據進行等權重加權，而事實上每個數據對擬合結果的重要性是不一樣的。針對采集的電路板點云，距邊緣區域較近的點云數據，其重要性在一定程度上小于內部區域的數據，本文提出基于自適應高斯權重的點云平面擬合方法，邊緣點看成是外點，區域內部點看成內點，通過三維高斯權重，確定各點分配權重的大小。算法原理如下。

對于n個點云數據，令擬合平面方程為

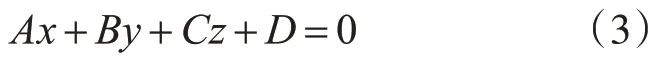
式（3）中，A、B、C、D為常數，并且A、B、C不能同時為零。要使空間平面擬合效果最佳，必須使所有點到平面距離的平方和最小，令di為點云中任意點到平面的距離，用式（4）表示：

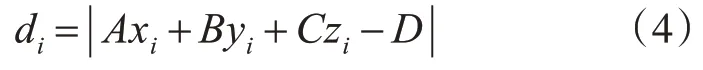
式中，(xi，yi，zi)為點云中任意一點，i∈{1，2，3，…，n}，用W表示三維高斯權重，利用下式計算：

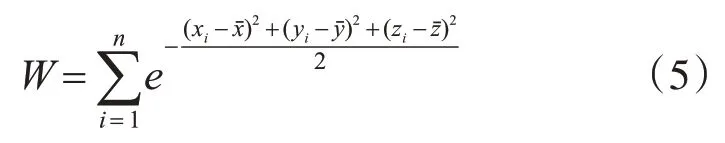
上式表明離中心點距離越遠的點，賦予權值越低，距離越近的點，賦予權值越高。通過拉格朗日求解極值的方法，令求解函數：

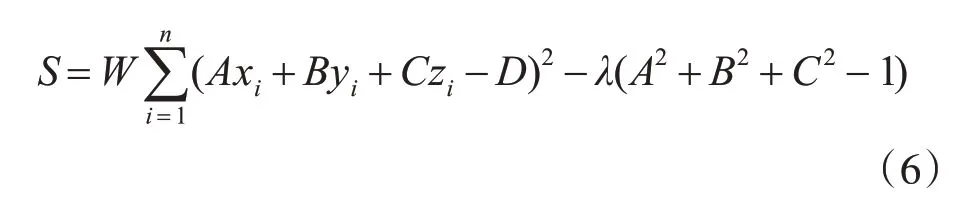
為使所有點到平面距離的平方和最小，利用S對D求偏導，令其為零，得

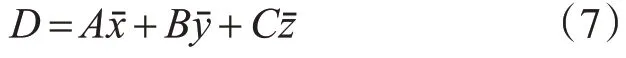
將式（7）代入式（4）中得

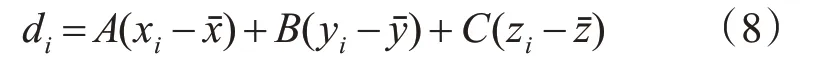
令Δxi=xi-xˉ，Δyi=yi-yˉ，Δzi=zi-zˉ，將變換后的式（8）代入式（6）中，然后S分別對A、B、C求偏導數并令其為零得

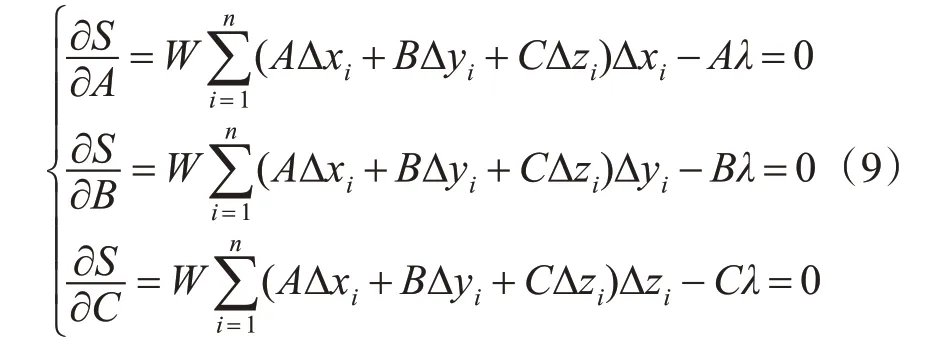
將上述方程組構成矩陣方程為

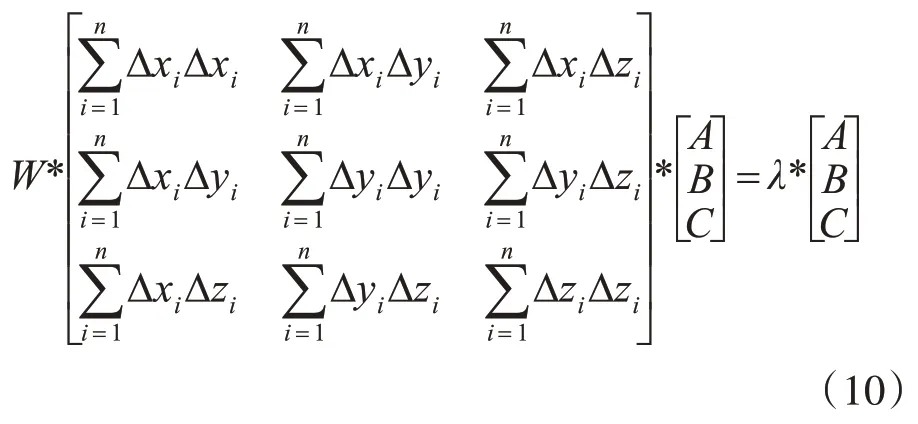
解式（10）方程組得A、B、C。將A、B、C的值代入式（7）得到D，這樣就得到擬合后的點云平面方程。圖4通過數據定量分析比較三種擬合方法處理后原始點到擬合平面距離的平方和。橫坐標x表示待擬合的點云數量，縱坐標y表示原始點云中每個點到擬合后平面距離的平方，本文將y的總和作為評價擬合好壞程度的指標，距離平方和越小，擬合效果越佳；從圖4看出，灰色波浪線起伏程度最低，與x軸組成的面積最小，說明本文方法擬合效果最好。

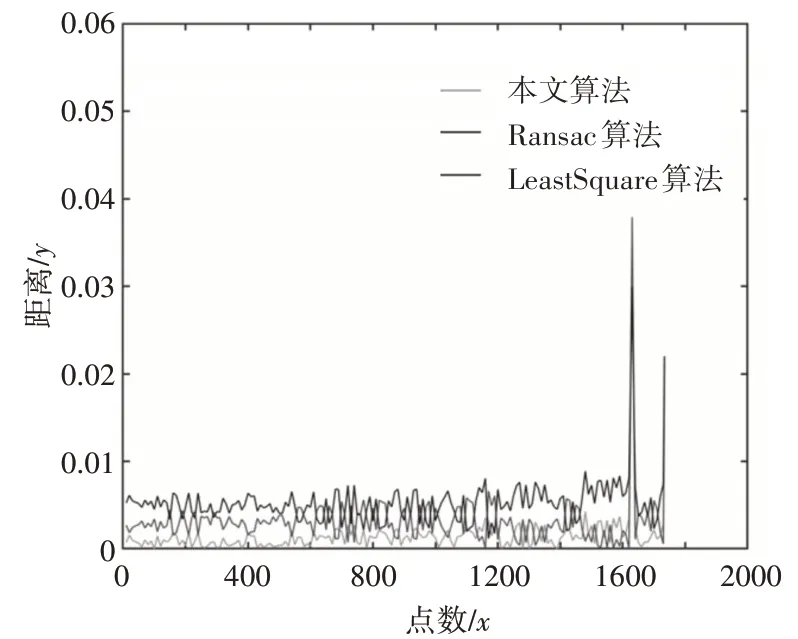
圖4 不同擬合方法比較結果圖

3.3 電路板元件參數計算

電路板元件與底板之間形成高度差異，可以通過擬合電路板元件上表面和底板平面計算兩平面之間的高度差。設擬合后電路板元件點云上表面平面方程為A1x+B1y+C1z+D1=0，擬合后電路板底板點云平面方程為A2x+B2y+C2z+D2=0，兩平面夾角的余弦關系為

式中，A1、B1、C1為元件上表面擬合平面參數，A2、B2、C2為電路板底板擬合平面參數。

當cosθ=1（即θ=0°）時，電路板底平面與元件上表面所在平面平行，通過式（12）計算得到高度差h：

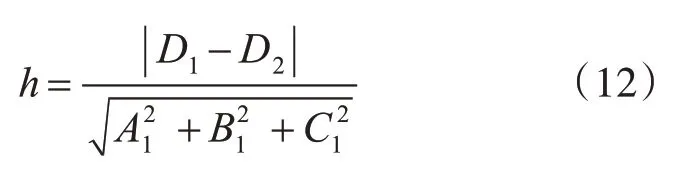
式中，D1為元件上表面擬合平面參數，D2為電路板底板擬合平面參數。

掃描獲取的點云數據中，往往只有少部分邊界點，邊界點與非邊界點存在明顯的區別，尤其在點云平坦區域［19］。對平面擬合后的目標點云進行邊界提取，如圖5所示，白色框內部分為擬合點云，白色部分為提取的邊界，假設目標平面在x方向上的最大值為xmax，最小值為xmin，長度l=xmax-xmin；同理假設目標平面在y方向上的最大值為ymax，最小值為ymin，則寬度w=ymax-ymin。

圖5 邊界提取

4 實驗結果

4.1 標準塊厚度測量

本文測量實驗采用型號為CHRocodile SE的光譜共焦傳感器，探頭工作距離為10mm，測量范圍為350μm～1425μm，光斑直徑為5μm；三軸運動控制器的型號為SMC606，本文測量實驗中設定軸運動速度3mm/s。

將標準塊與X軸平行放置，通過三軸精密位移平臺驅動傳感器移動，調節到傳感器聚焦的位置，然后控制X軸、Y軸開始掃描。圖6（a）是待測的標準塊實物，圖6（b）是對標準塊采集后的三維點云顯示，對圖6（b）進行半徑濾波處理得到圖6（c），圖6（d）是標準塊點云實體化顯示圖。

圖6 標準塊實物和三維點云顯示

通過本文擬合方法，對濾波后標準塊上下表面點云分別進行擬合，計算得到上表面點云中A=0.00055，B=-0.00194，C=0.99998，D=-0.28913，所以上表面擬合平面方程為

下表面點云中A=-0.00003，B=-0.00289，C=0.99995，D=0.70871，所以下表面擬合平面方程為

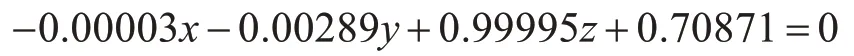
由式（11）得到cosθ=0.99998，所以擬合后標準塊上下表面相互平行，由式（12）得到標準塊厚度h=0.99793mm。

表1給出通過RANSAC擬合、LS擬合和本文方法擬合后標準塊上下表面方程參數。表2是對1mm標準塊厚度進行測量的結果，并將本文擬合方法處理結果與RANSAC擬合和LS擬合處理后進行比較。

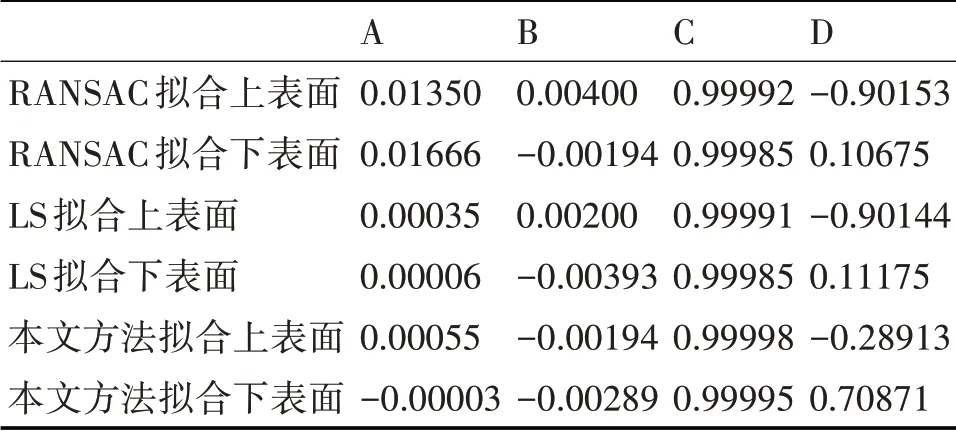
表1 不同方法擬合后標準塊上下表面方程參數

從表2可以看出，通過RANSAC方法和LS方法對濾波后的點云進行空間平面擬合，得到標準塊厚度誤差分別為9.34μm和15.64μm；使用本文提出的基于自適應高斯權重的點云平面擬合方法處理后，標準塊測量誤差減小到1.09，說明本文提出擬合方法的有效性比RANSAC方法和LS方法強。

表2 不同方法擬合后測量結果比較

4.2 電路板元件測量

本文對圖7（a）所示電路板上的元件進行3D高精度檢測，由于采集3D點云數據量大，在文中顯示效果不明顯，所以將圖7（a）框選區域放大顯示。圖8（a）是光譜共焦系統對圖7（b）的3D點云顯示，圖8（b）是對圖8（a）實體化顯示。

圖7 電路板實物圖

圖8 電路板點云顯示圖

對圖7（a）中序號標記的十個電容塊進行測量，它們的三維測量結果如表3所示。針對表3測量所得高度數據的誤差分析，如表4所示。由表4可以得出結論，以十個元件高度測量的平均值為標準，最大高度誤差為7.95μm，最小高度誤差為1.46μm，高度測量結果穩定，滿足高精度檢測要求。

表3 電路板元件三維尺寸測量結果

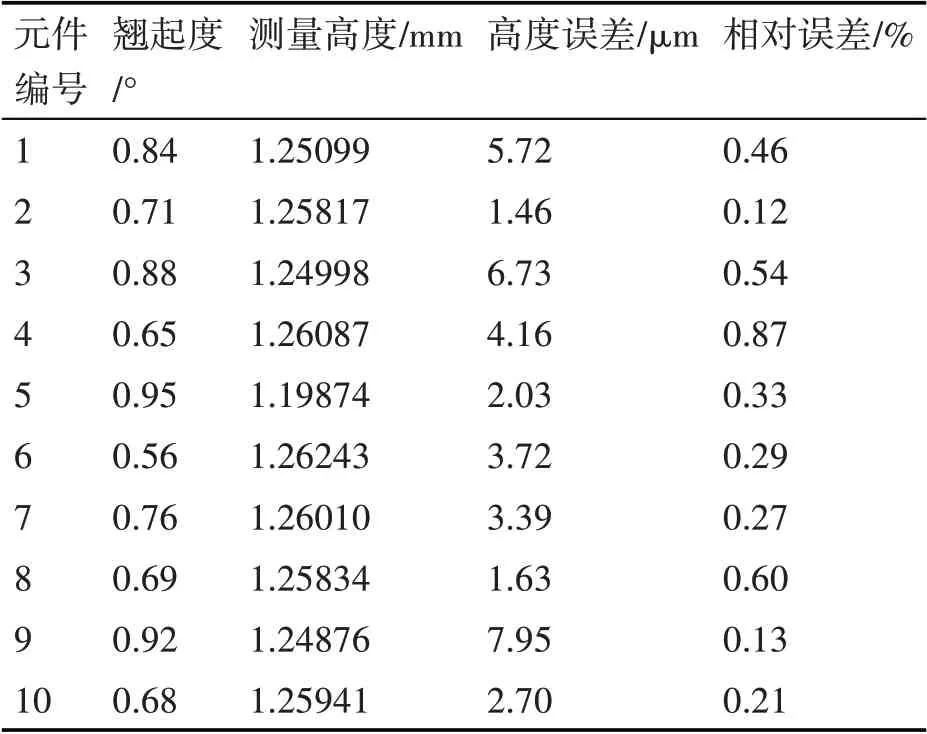
表4 測量高度誤差分析

5 結語

本文采用基于光譜共焦傳感器的電路板元件檢測系統，通過分析系統的組成和檢測原理，實現對電路板微型元件的高精度3D檢測。在對電路板元件3D點云數據處理過程中，提出基于自適應高斯權重的空間點云平面擬合方法，通過對標準塊厚度測量，驗證了本文提出方法測量誤差小、精度高。針對電路板上十個相同類型元件高度進行檢測，精度能達到1.46μm。本文提出的方法能夠滿足工業測量的精度和速度要求，具有一定的工程應用價值。