基于兩種建模方法的冗余并聯機器人的動力學對比研究＊

郝亮亮 劉小娟 杜 婷 閆獻國

（①太原科技大學能源與材料工程學院，山西 晉城 048011；②山西科技學院，山西 晉城 048011）

并聯機器人經過近30 年的發展和國內外學者的研究，因其具有輸出精度高、剛度大和承載能力強和整體結構緊湊等優勢[1]，已廣泛應用于康復醫療[2]、飛機裝配[3]、分揀包裝搬運[4-5]和打磨機構[6]等。其中冗余并聯機器人是具有更大的承載能力、更高的剛度和更高的定位精度且可輸入構件數多于機構輸出自由度的并聯機構[7]，因此受到了研究者的廣泛關注，成為國內外機器人和機構學領域的研究熱點[7-10]。

2-UPR/2-RPU 并聯機器人是五軸混聯磨床試驗機的核心機構，需要系統輸出按照期望位姿及軌跡路線穩定前行，在工作過程中受到動態載荷的影響使其控制難度增加，因此為了改善機構的力學性能，運動學及動力學模型是并聯機構特性分析的基礎。研究人員常用的動力學建模方法有包括牛頓-歐拉法[1]、拉格朗日法[7]、凱恩方程法[10]和虛功原理法[11]等。其中拉格朗日法以其方程表達清晰且結構緊湊，無理想約束力的優點成為冗余并聯機器人最常使用的方法；而虛功原理則是以機構為整體，用廣義坐標消除約束力和關節慣量，因此其方程形式簡單[12]。

但是由于冗余并聯機構結構復雜、構件數量較多，因此采用傳統的方法求解其動力學方程極為復雜，而引入螺旋理論結合傳統動力學方法建立的動力學方程適用于復雜機構的運動學和動力學的研究，目前已經應用于復雜并聯機構的研究中。韓博等[13]應用螺旋理論求解了機構的速度及雅可比矩陣，推導了各桿件的角加速度與質心線加速度，運用牛頓-歐拉方程和虛功原理方法相對四面體3RR-3RRR 可展機構的動力學進行了分析仿真，結果表明此方法分析過程簡單且易編程計算。張榮敏等[14]采用旋量理論下的牛頓-歐拉方程構建了2 自由度解耦球面并聯機器人的動力學方程。陳原等[15]以復合式移動機器人球面并聯腿機構為研究對象，運用影響系數法推導速度和加速度影響系數矩陣，采用拉格朗日方法建立了球面并聯腿機構的動力學模型，并應用數值仿真法驗證了模型的正確性。柴馨雪等[16]采用螺旋理論結合虛功原理對2-UPR-RPU 并聯機器人復雜運動狀態下的動力學特性并進行了分析。李二偉等[17]基于螺旋理論建立了大型重載并聯穩定接貨平臺的動力學解析模型。高名旺等[18]用螺旋理論推導了4-RRR 冗余并聯機構的雅可比矩陣，采用牛頓-歐拉法計算主元點的慣性力螺旋，運用虛功原理構建了機構的動力學公式。林光春等[19]針對新型2-UPR/2-RPU 結構冗余并聯機構采用虛功原理成功構建了該機構的動力學模型，結合驅動力二范數的最優方法對機構的驅動力和驅動功率方程進行了推導。

為驗證兩種動力學建模的正確性，采用螺旋理論和拉格朗日法建立并聯機器人的動力學模型；在MATLAB 中編程得到并聯機構的算法，求解得到動力學模型各支鏈驅動力數值仿真結果，并通過與ADAMS軟件的動力學仿真結果進行仿真驗證和誤差分析。

1 冗余并聯機器人運動學建模

2-UPR/2-RPU 并聯機器人的機構簡圖和虛擬樣機圖如圖1 所示，其由固定在機床上的定平臺、包含冗余移動副驅動的2 條UPR 支鏈和2 條RPU 支鏈以及末端執行的動平臺3 部分組成，整個機構呈對稱分布。其中Mi(i=1,2)為動平臺上R 副的中點且與支鏈UPR 的R 副中點重合，Mi(i=3,4)為支鏈RPU 與動平臺相連的U 鉸中心點，Si(i=1,2)為支鏈UPR 與定平臺相接連的U 鉸中心點，Si(i=3,4)為分支支鏈RPU 與動平臺相連的R 副中心點。

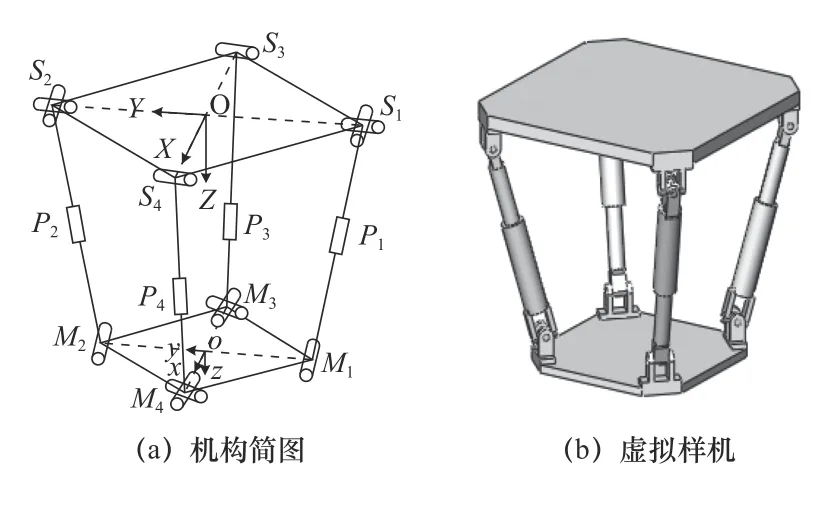
圖1 并聯機器人機構簡圖和虛擬樣機圖

在定平臺幾何中心處建立O-XYZ全局坐標系和位于動平臺處的動坐標系o-xyz，邊長分別為a和b的正方形M1M2M3M4、S1S2S3S4，該冗余驅動并聯機器人的自由度[20]為2R1T，共有3 個自由度。在全局坐標系下點Mi(i=1,2,3,4)的矢量坐標分別為

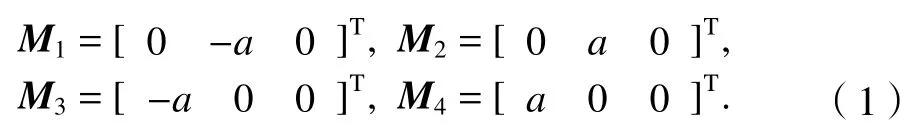
點Si（i=1,2,3,4）在動坐標系下的坐標矢量為

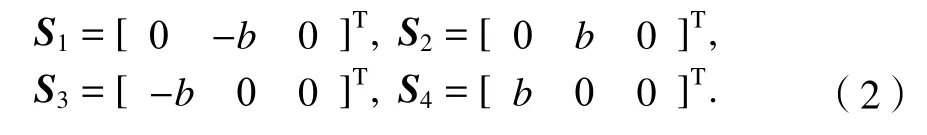
2-UPR/2-RPU 并聯機器人的驅動位于P副處為機構的主動關節位置，設機構末端位置點o處的坐標矢量為：P=(x,y,z)T，各支鏈的移動位移量為li(i=1,2,3,4)。采用Z-Y-Z型姿態歐拉角(α,β,γ)及坐標變換原理可以將旋轉變換矩陣表示為

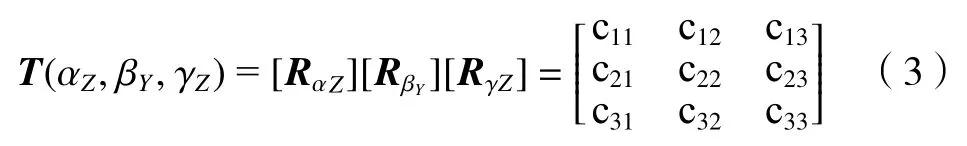
式中：c11=cosαcosβ，c21=sinαsinβ，c12=cosαsinβsinγcosγsinα，c13=cosαsinβcosγ+cosγcosα，c22=sinαsinβ sinγ+cosγcosα，c23=sinαsinβcosγ-cosαsinγ，c31=-sinβ,c32=cosβsinγ，c33=cosβcosγ。RαZ、RβY和RγZ分別代表繞Z軸、Y軸和Z軸的轉換矩陣，因此2-UPR/2-RPU 并聯機器人可以根據機構位姿確定動平臺點Mi由o-xyz坐標系轉換到O-XYZ坐標系中的坐標如下

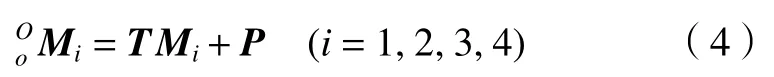
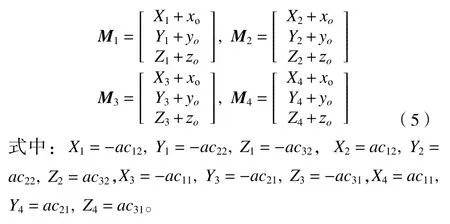
根據圖1 可得如下閉環矢量方程

式中：li為各支鏈中移動關節的矢量；Si表示從點O到點Si的矢量；定義矢量ei(i=1,2,3,4)分別代表轉動關節Mi中心線的且模為1 的矢量。

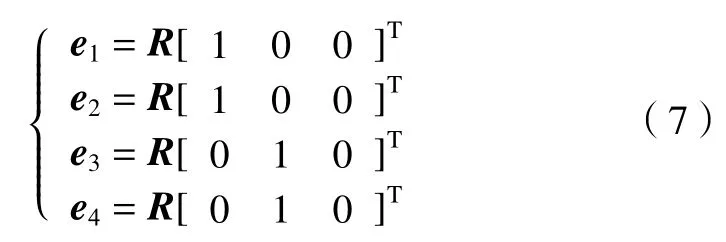
由幾何關系可得機構的約束條件

由機構的幾何特征及兩點的距離公式可得

對式（1）～（7）整理可得

因此，由式（1）～（10）結合MATLAB 程序求解可得到2-UPR/2-RPU 冗余并聯機器人的位置反解；而冗余驅動并聯機器人的反解求解過程是已知位姿求解各支鏈移動副的位移量li，而且冗余并聯機器人的反解求解過程相對簡單且其解具有唯一性；2-UPR/2-RPU 冗余并聯機器人的位置正解與其反解求解過程正好相反，是已知驅動副Pi的驅動位移來求解動平臺位姿。

2 基于拉格朗日方程的動力學建模

2-UPR/2-RPU 冗余并聯機器人是由多個剛體構成的組合系統，其拉格朗日算子L表述為

式中：T為動能，V為勢能。機構系統的運動方程以拉格朗日方程表示為

式中：n為桿件總數；qi為系統的廣義坐標變量；為廣義速度；Fi為影響第i個廣義坐標的廣義力或廣義力矩。將拉格朗日算子代入式（12）得

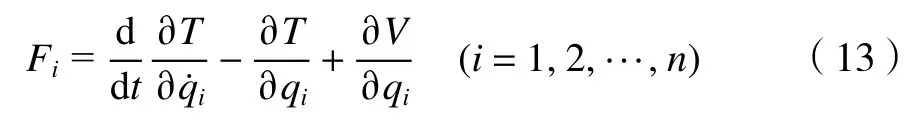
因此，機構的系統勢能V僅是關于qi的表達式，而動能T是關于qi，及時間t的表達式，接下來求解機構各個構件的速度。而機器人動平臺的速度可以用如下矩陣表示

式中：Kp為動平臺速度關于廣義速度的映射關系矩陣，其形式為

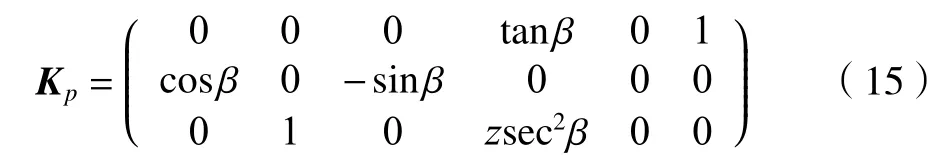
而vp=(ωT)T為動平臺的速度矢量，ω為動平臺的角速度矢量，為動平臺的線速度矢量。

而2-UPR/2-RPU 并聯機器人動平臺中心點的加速度可以通過對式（14）求導得到

下面以分支1（UPR 分支）為例闡述并聯機構分支速度分析方法，依據末端執行器的運動可知分支1 轉動副對應轉動軸的速度為

式中：a為動坐標系原點指向轉動副中心的向量。根據速度合成定理將vRi映射到驅動桿軸向可得主動速度

式中：zLi是驅動支鏈軸向單位矢量，Li為移動副桿件長度。根據冗余并聯機構的幾何位置關系，轉動副的速度可以用下式表述

式中：ωLi為桿件角速度；將式（19）兩邊同時叉乘zqi，同理推導出桿件的質心速度vZi

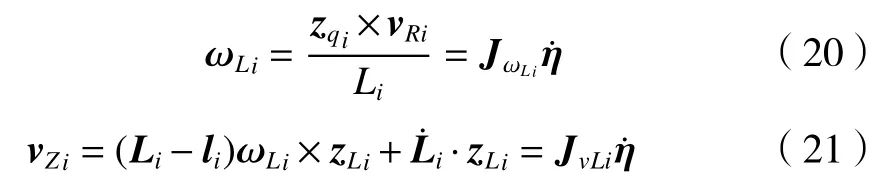
根據式（11）～（21）即可求得到機構的廣義力，但逆動力學建模需要求解機構的主動力，因此使用虛功原理描述機構的主動力與廣義力間的關系，設機構的廣義坐標為θ、δ、ψ，則其對應的廣義力和虛位移分別為qθ、qδ、qψ和Δθ、Δδ、Δψ。因此在移動副驅動力Fi驅動下，機構的總虛功為

因此可以得到：

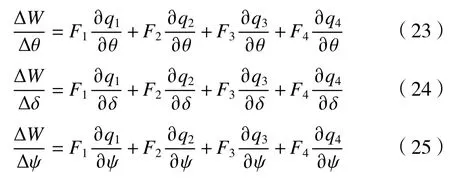
由式（23）～（25）可得廣義力和驅動力間的雅可比矩陣JT為

將式（12）～（26）聯立可得并聯機構的動態方程

即為2-UPR/2-RPU 冗余并聯機器人的逆動力學方程。

3 基于螺旋理論的動力學建模

下面本文運用螺旋理論對2-UPR/2-RPU 冗余并聯機器人并以分支1（UPR）為例進行速度和加速度分析。首先建立如圖2 所示的螺旋系

圖2 UPR 分支簡圖

設點M1的坐標為(xM1,yM1,zM1)T，則分支1 的螺旋系有

用ω1i(i=1,2,3,4)表示分支1 各個關節速度，則式（14）可表示為

其矩陣形式為

因此2-UPR/2-RPU 冗余并聯機器人每個分支的驅動關節速度可以表示為

進一步化簡可得分支i中第j個關節的速度與各個分支驅動速度之間的關系

因此分支i中第j個關節的質心速度螺旋為

式中：dijCe為從原點到分支的i中第j個桿件質心點的位置矢量。在定坐標系下分支1 末端加速度可以表述為

因此，由式（34）可以推導出分支i中第j個桿件的速度螺旋為

下面根據虛功原理來推導該機構動平臺受到的力和力矩為

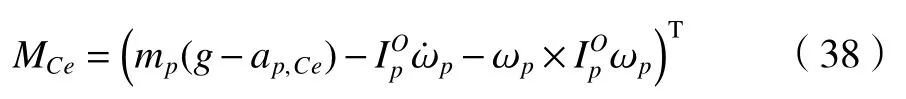
式中：動平臺質量為mp，重力加速度為g，動平臺質心線加速度為apCe，動平臺相對于定坐標系的慣性張量為IOp，動平臺角速度為ωp。而作用在分支i上第j個桿件質心處的力螺旋為

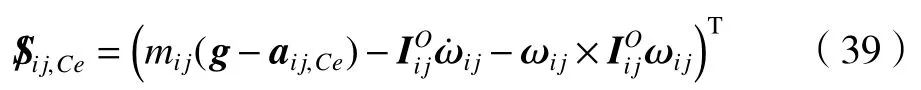
因此2-UPR/2-RPU 并聯機器人的總功為

由虛功原理可得

式（40）～（41）中：Δvi j,Ce和為虛速度且其值為任意值，根據虛功原理2-UPR/2-RPU 并聯機器人的總虛功始終為零，故有

因此由式（42）可計算得2-UPR/2-RPU 并聯機器人驅動副的驅動力數值。

4 兩種方法下動力學仿真分析對比

接下來在SW 建模軟件中建立2-UPR/2-RPU 并聯機器人的3D 模型，以Parasolid(*.x_t)文件導入動力學仿真軟件ADAMS 中，通過ADAMS 來驗證采用朗格朗日方法和螺旋理論方法所建立的冗余2-UPR/2-RPU 并聯機器人動力學模型的正確性，在ADAMS 中建立如圖3 所示的動力學模型添加構建關系并設置各項參數。

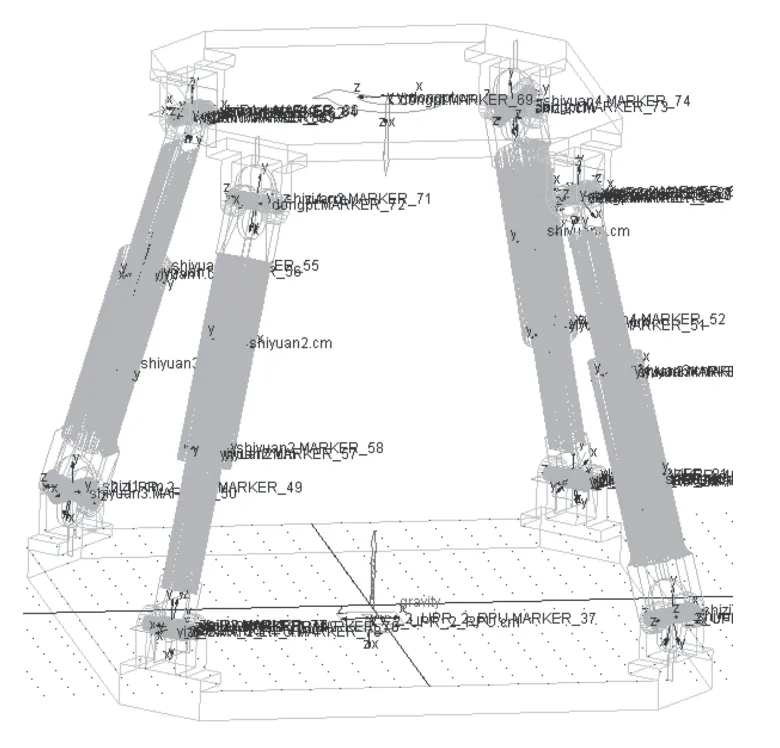
圖3 并聯機器人ADAMS 動力學模型

設動平臺和定平臺的邊長分別為a=250 mm 和b=400 mm，及動平臺中心點軌跡方程為

式中：t0為期望持續時間，其值為0.5。在軟件MATLAB 的中建立并聯機器人的模型，以運動學和動力學模型為基礎，編程得到并聯機構的算法，將以螺旋理論和拉格朗日法建立的并聯機器人動力學方程為輸入，仿真后得到機器人的分支鏈驅動力與ADAMS 輸出的動力學仿真分支鏈驅動力數據并得到圖4 所示的在動平臺中心點軌跡方程驅動下的驅動力隨時間變化圖。

從圖4 中可得，基于拉格朗日方程和螺旋理論求解的支鏈驅動力和ADAMS 軟件仿真求解的支鏈驅動力數值變化曲線整體是一致的，從而驗證了采用這兩種方法所建立的2-UPR/2-RPU 并聯機器人的動力學模型是正確的，在運動周期內，最大驅動力出現在驅動桿支鏈1 處為269.3 N。同時數據也存在區別，下面對兩種方法的求解結果進行誤差分析，利用MATLAB 編程功能將圖4 中計算數據按照以下計算方法：給定軌跡數值與理論值之差在該時刻驅動力所占ADAMS 理論值的百分比進行誤差分析，求解得到2-UPR/2-RPU 并聯機器人的各鏈驅動力誤差隨時間變化曲線如圖5。

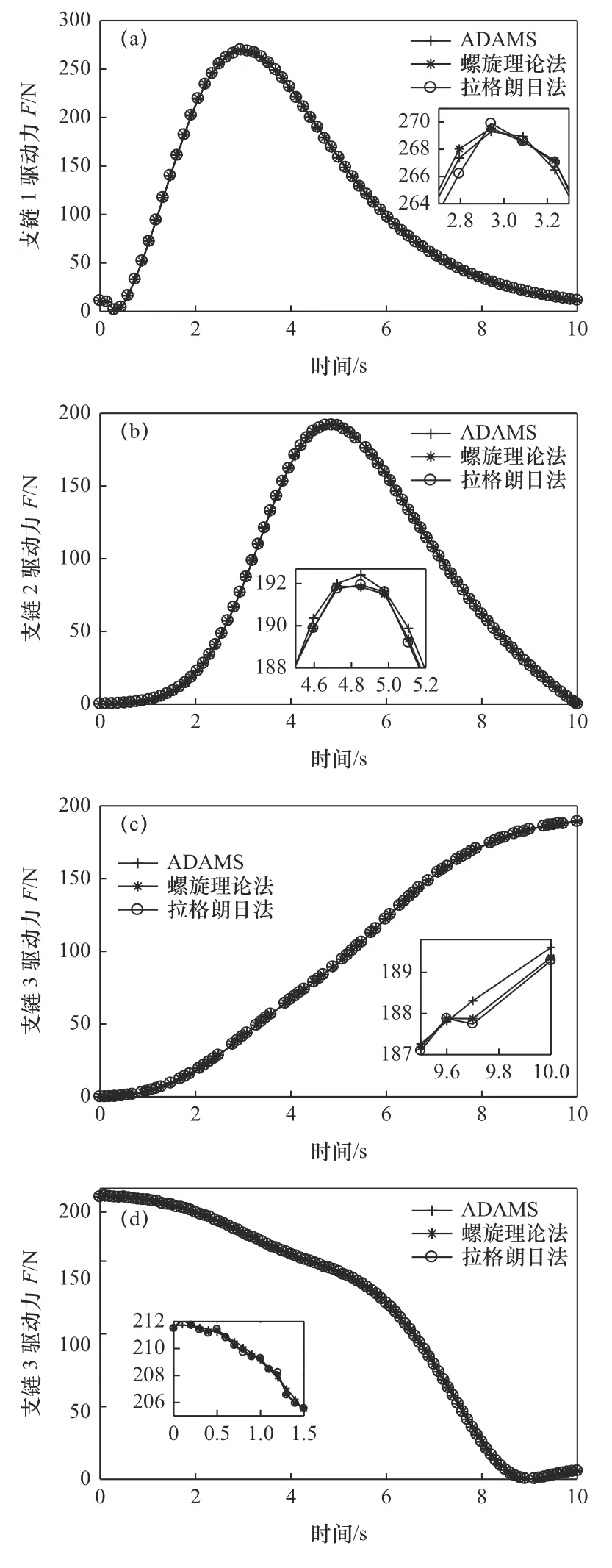
圖4 各支鏈驅動力求解結果曲線

從圖5 可以看出，各支鏈中采用螺旋理論法動力學建模求解出的驅動力誤差的最大值和最小值為：驅動桿1 的驅動力相對最大誤差為0.43%和0.452%、約0.515 N 和0.527 N；驅動桿2 的驅動力最大誤差為0.34%和0.381%，約0.580 N 和0.649 N；驅動桿3 的驅動力相對最大誤差為0.281%和0.295%，約0.324 N 和0.336 N；驅動桿4 的驅動力相對最大誤差為0.181%和0.252%，約0.381 N 和0.529 N；因此，螺旋理論法和拉格朗日法求解結果相對誤差較小，并且處于合理范圍。

圖5 各支鏈驅動力誤差圖

而在使用MATLAB 軟件進行數值求解后得出了這兩種方法的優缺點：拉格朗日方程的建模過程相對簡單，但在MATLAB 軟件進行編程數值求解時計算量大且費時；螺旋理論法模型建立過程簡單、邏輯清晰，在數值求解時計算量小且速度快。

5 結語

（1）采用封閉矢量法建立了并聯機器人的運動學反解方程，求解過程簡單且解具有唯一性。

（2）采用螺旋理論對2-UPR/2-RPU 并聯機器人各關節和桿件的速度和加速度進行分析，建立并聯機器人的動力學模型。

（3）采用拉格朗日法求解了并聯機器人機構部件的速度關系并建立了其動力學模型。

（4）通過在MATLAB 中編程得到與ADAMS軟件的動力學仿真結果對比圖并進行仿真驗證和誤差分析。結果表明：螺旋理論建立的動力學模型精度相對較高、方法方便理解、計算簡單、精度高、更適用于少自由度并聯機構動力學模型的建立和機構動力學的控制；滿足磨床打磨曲面的精度要求，為機構的實踐應用提供了可靠的理論依據并奠定了重要基礎。