基于回路分析的配電網電壓及網損靈敏度分析方法

朱雪原

（國網江蘇省電力有限公司豐縣供電分公司，江蘇徐州，221700）

0 引言

分布式電源能夠使配電網編程多種電源系統，介入分布式電源后，主要是要對分布式電源的配電網進行分析。就目前而言，有很多的學者對配電網進行了研究，并推算出了很多種算法，其中最有代表的就是Zbus高斯法、改進牛頓法、回路阻抗法以及回路分析法。分析網絡損耗靈敏度時，主要運用的方法是雅克比法、伴隨網絡法等等，雅克比法的應用時最為廣泛的[1]。在計算靈敏度的過程中，對數據的要求比較低，計算起來比較容易。根據雅可比矩陣的基本理論，建立起線性靈敏度的模型，如果注入的功率較大，可能會出現耦合作用。所以說，本文將會通過回路分析法對配電網電壓以及網絡損耗靈敏度進行分析，配電網拓撲結構以及系統參數不會出現改變，接入分布式電源，并且構建節點電壓以及雅克比靈敏度矩陣。這樣就可以改變分布式電源的位置，分析分布式電源對配電網所造成的影響，這對于配電網的回路分析起著非常關鍵的作用[2]。

1 電壓波動理論

由于配電網潮流分布出現了變化，這樣就會間接造成配電網上的節點電壓出現波動，如果將系統當中的兩個節點當做是a和b，電流的方向是從a到b，Ua、Ub表示為兩個節點上的電壓。R+jX表示兩個節點之間的阻抗，Pb、Qb表示b節點的有功功率和無功功率[3]。具體如圖1所示。

圖1 線路ab的等值電路

就可以得到電壓損耗的公式（1）：

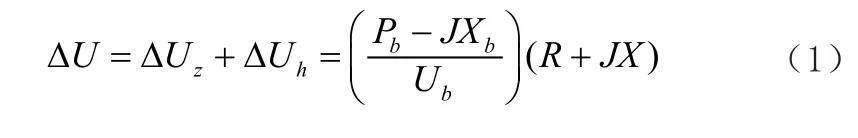
在這個公式當中，ΔU、ΔUh表示電壓出現變化的縱橫分量，忽略兩個節點中的電壓橫分量，就可以得到公式（2）。

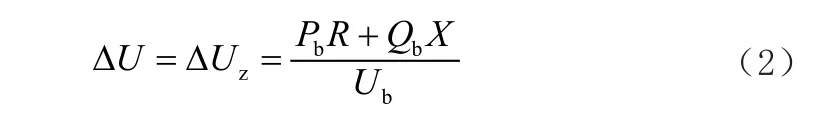
2 接入分布式電源前后效果分析

首先，需要對兩個比較簡單的配電網系統進行分析，一個接入分布式電源，一個不接入分布式電源。并且觀察其應用效果。接入分布式電源圖為圖2所示，未接入分布式電源為圖3所示。

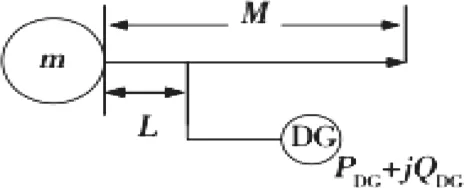
圖2 接入分布式電源效果圖

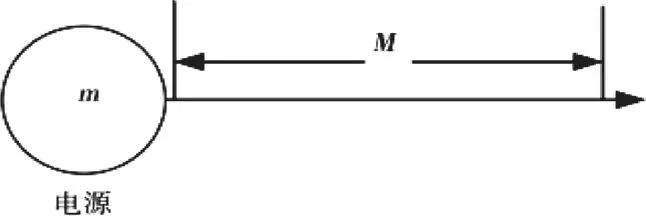
圖3 未接入分布式電源效果圖

由于分布式電源接入后，對電壓所產生電壓影響較小，所以可以忽略對電壓產生的影響。在回路分析中的電壓相等。將分布電源的諸如容量設置為PDG+jQDG，在回路分析的線路阻抗設置為R+jX，分布式電源與電源的長度為L，電源與負荷端之間的長度為M，就能得知配電網中的線路損耗主要由節點與分布式電源的線路損耗以及分布式電源到負荷端的線路損耗所組成，分別設置為P1與P2，就能夠得到公式（3）、公式（4）、公式（5）。

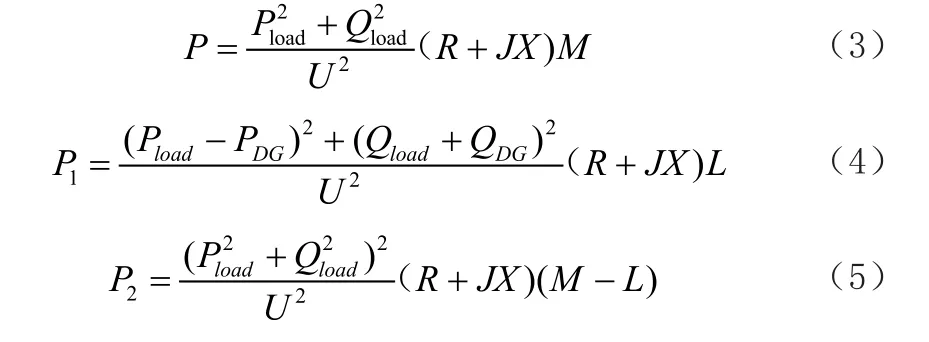
由以上的公式還可以得出，當配電網接入了分布式電源之后，線路的損耗主要與分布式電源接入的位置、容量以及功率有著密切的關系[4]。如果負荷容量為兩倍，諸如的容量小于負荷容量，就能夠在一定程度上降低配電網中線路的損耗，如果諸如的容量高于負荷容量時，就會加大配電網中線路損耗的程度。

3 回路分析

將以回路分析為基礎，接入回支關聯矩陣，關于矩陣B的概念如下：Bij等于1時，支路在回路中，并且方向是一樣的；當Bij等于-1時，支路在回路中，但方向不一致，是相反的；當Bij等于0時，支路不在回路中。

關于配電網的編號有兩項原則：①將配電網中的節點設置為O，節點O作為配電網的起點，另一個節點i為重點，那么就可以標記i；②根據支路的方向，判定支路節點的起點和終點，根據標準支進行編號。具體如圖4所示。

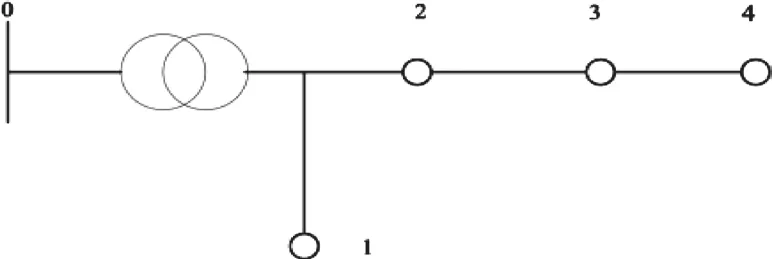
圖4 節點配電網圖

根據該圖即可得到回支關聯矩陣B：

引入回支阻抗矩陣ZLN后得到以下結果

拆分過后得到{ZLN}={RLN}+J{XLN} （RLN表示回支電阻矩陣，XLN表示回支電抗矩陣）

如果將配電網的節點O以及節點的電壓進行恒定，就能夠得到不介入分布式電源時的方程公式。如公式（6）所示。

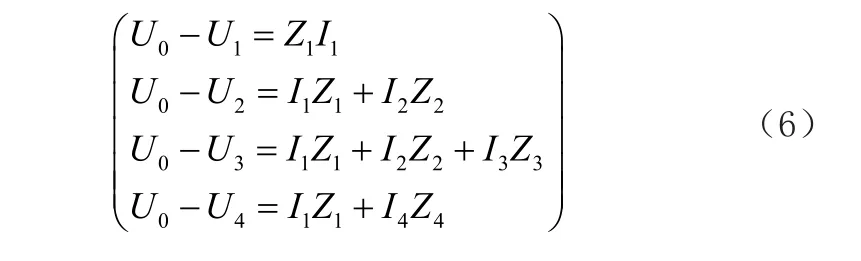
接入分布式電源時的方程公式如公式（7）所示。

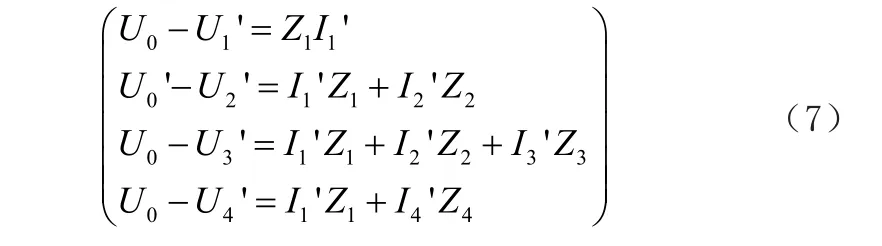
將兩個公式結合之后就能夠得到公式（8）。

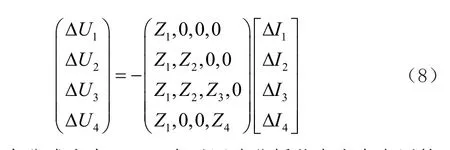
在這個公式當中，ΔUi表示回路分析節點當中電壓的變化矩陣，ΔIi表示回路分析中支路電流的變化矩陣。

從兩者的對比中，可以得到結果，當分布式電源接入到配電網當中的時候，拓撲結構以及線路阻抗不會出現改變，節點發生改變與支路中的電流變化有著密切的關系，由于分布式電源的接入，支路電流受到了一定的影響，由原來的單一配電網絡形成了多系統配電網絡，負荷出現了變化，然而分布式電源也會根據電流的實際情況反饋到網絡中的各個節點當中[5]。出現這樣的狀況之后，分布式電源所接入的節點都會被當做是線段的末端節點，從而對回路當中的電流產生一定的影響，成為了配電網參數變化的關鍵所在。回路中電流靈敏度矩陣節點電壓表示為Ui=Ui∠0，于是{ΔIi}={ΔIzi}-j{ΔIhi}，構建出電流中的縱分量以及橫分量的靈敏度矩陣，如公式（9）、公式（10）所示。

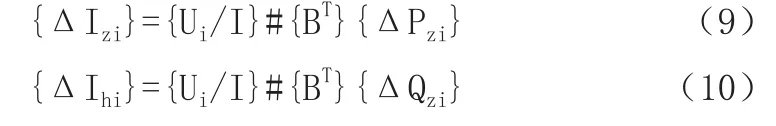
在這兩個公式當中，{Ui/I}表示節點中電壓的一維列向量，ΔPzi表示接入分布式電源后節點功率變化的一維列向量[6]，ΔQzi表示接入分布式電源無功變化的一維列向量，#為矩陣相乘。

4 電壓網損靈敏構建方式

首先，對節點中電壓的縱分量靈敏度矩陣公式進行分析，如公式（11）所示。

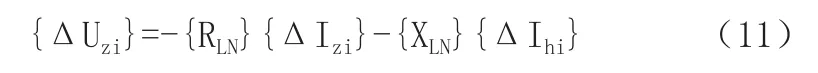
在這個公式當中，RLN表示回路電流中的電阻矩陣，XLN表示回路電流中的電抗矩陣。構造步驟大致分為以下四步。①首先需要明確線路中的初始數據；②其次要通過配電網中的拓撲結構建設回路直流的關聯矩陣，回路直流中的電阻矩陣以及回路直流中的電抗矩陣；③隨后建設電流的縱分量與橫分量的靈敏度矩陣；④建設節點電壓中的縱分量矩陣[7]。

其次，對線路損耗的靈敏度矩陣進行分析，得到公式（12）。

在這個公式當中，可以能夠得到支路中的功率變化參數，#表示矩陣位置相乘。構造的步驟分為以下五步：①首先，要明確支路節點中符合功率的一維列向量，并通過回路直流的關聯矩陣進行相乘，就能夠得到初始節點功率矩陣；②借助初始節點支路注入的節點與相對應的節點電壓矩陣進行計算，就能夠得到初始的電流橫分量矩陣與電流縱分量矩陣；③了解線路中的阻抗，構建一維列向量；④了解線路損耗靈敏度矩陣；⑤了解網損靈敏度。

5 仿真分析

進行仿真分析時，將以IEEE33的節點為例子，并在節點中的5,10,27分別接入分布式電源，額定功率為700kw，如圖5所示。

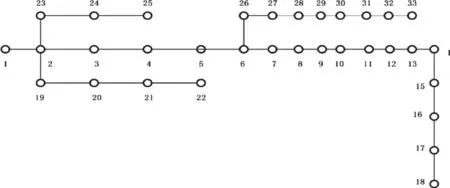
圖5 IEE33節點系統

考慮到饋線末端比較敏感，尤其是對節點電壓的變化，所以就選擇節點17進行仿真分析。計算靈敏度矩陣的變化值小于潮流計算的準確值，而靈敏度矩陣的變化值也與潮流計算的準確值中的誤差有著緊密的聯系，分布式電源增大，誤差會減小。如圖6所示。

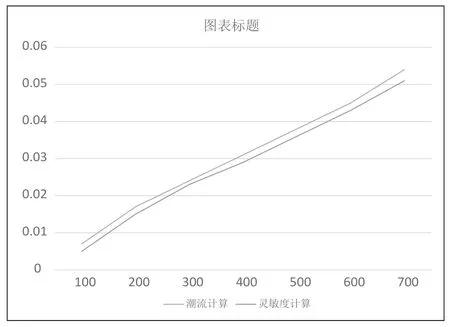
圖6 節點17電壓變化對比

在仿真分析的過程中，700kw的功率各個節點的電壓都會出現變化，節點5—節點17的變化比較大，1—4的變化較小。也就是說，本次所研究的電壓靈敏度矩陣法有較高的應用價值，當分布式電源的功率越大，節點中的精度仍然能夠得到保證，如圖7所示。

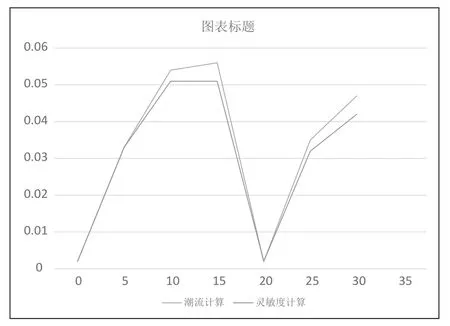
圖7 各節點電壓變化情況

6 結束語

本文通過回路分析法，并且接入了分布式電源，分析回路電流中的關聯矩陣和回路電流中的阻抗矩陣，通過矩陣構造出電壓靈敏度矩陣，隨后分析線路損耗的靈敏度矩陣，得到網絡損耗靈敏度。一般來說，通過靈敏度矩陣的設計，并不會改變拓撲結構當中的參數，還可以快速得到比較準確的運行參數。在這樣的情況下，對IEEE33當中的17節點進行了仿真分析，以此來驗證本次研究的有效性和準確性。在驗證的過程中，當分布式電源接入的功率越大，誤差也會越來越小，適合解決配電網中的運行問題[8]。