微電網最小化通信鏈路優化算法

劉明宇， 李曉麗， 王千千

(東華大學 信息科學與技術學院， 上海 201620)

微電網由多種分布式電源、儲能、負載以及相關監控保護裝置構成，既可以與電網并網運行，也可以孤島運行。作為一種新的電網結構，微電網的出現順應我國高質量的新發展理念。將多種分布式電源以微電網的形式集成并靈活并網是利用分布式電源的有效方式[1-4]。基于分布式一致性理論，將微電網中的分布式電源抽象成多個智能體，在多智能體中變量隨時間變化趨于一致的收斂速度顯得尤為重要，系統的收斂速度主要取決于多智能體連通圖拉普拉斯矩陣的第二小特征值(又稱代數連通度)。在此基礎上，Bidram等[5-6]利用神經網絡理論研究微電網二次控制自適應等問題。李遠哲[7]提出一種基于網絡拓撲優化的多微電網系統分布式協同控制方法，該方法在強化學習的基礎上利用Q-learning算法實現拓撲結構的優化，旨在實現微電網群的全局協同控制，并消除中央控制器的必要性，但是需要大量的數據支撐。沈政委等[8]就改變拓撲結構工具的輸電線的若干開斷問題和電網電壓的控制問題進行了綜述，但是沒有給出具體的算例分析和解決方案。呂振宇等[9]提出一種利用一致性算法對微電網二次控制進行優化的方法，但是在實現拓撲優化的算法中采用了傳統的Warshall算法，該算法的缺點在于運算速度慢，在微電網中的應用規模較小。于芃等[10]對微電網并網、離網切換問題進行了模塊化分析，實現了平滑切換，但是本質上沒有改變拓撲結構，因而系統的收斂速度和通信成本不變。

為了降低微電網運行的通信成本，在傳統微電網控制的基礎上，對微電網通信層的拓撲結構進行鏈路最小化分析。將分布式電源抽象成多智能體，在圖論的技術上著重研究各個節點的通信連接方式對系統的收斂速度的影響，利用靈敏度和梯度下降思想設計一種通信鏈路最小化算法。該算法對系統連通圖的邊進行適當刪減，在保證拓撲結構為全連通圖的前提下，最大化代數連通度，最小化通信連接的邊數，從而將微電網的通信成本降到最低。

1 微電網控制的數學模型

分布式電源的控制策略直接決定微電網能否穩定運行，風力發電系統、光伏發電站、微型燃氣機及儲能系統等作為分布式電源通過電力電子變流裝置并入大電網，使得微電網在常規模式下具有兩種運行狀態，即并網運行和離網運行，后者又稱孤島運行。在微電網無功功率分配的基礎上進行鏈路最小化分析。

一般孤島運行的微電網采用下垂控制解決功率的分配問題，下垂控制通過模擬傳統發電機組的功頻特性，使所有分布式電源共同參與功率分配以維持系統頻率和電壓的穩定。通常將微電網中的分布式電源與母線連接簡化成圖1所示電路，其中：Ub∠0為公共母線的電壓(符號∠為電氣工程中相位符號)；U∠δ為分布式電源的輸出電壓；δ為電壓功角；Z∠θ=R+jωL為分布式電源的等效阻抗；S為分布式電源的視在功率；P和Q分別為有功功率和無功功率。

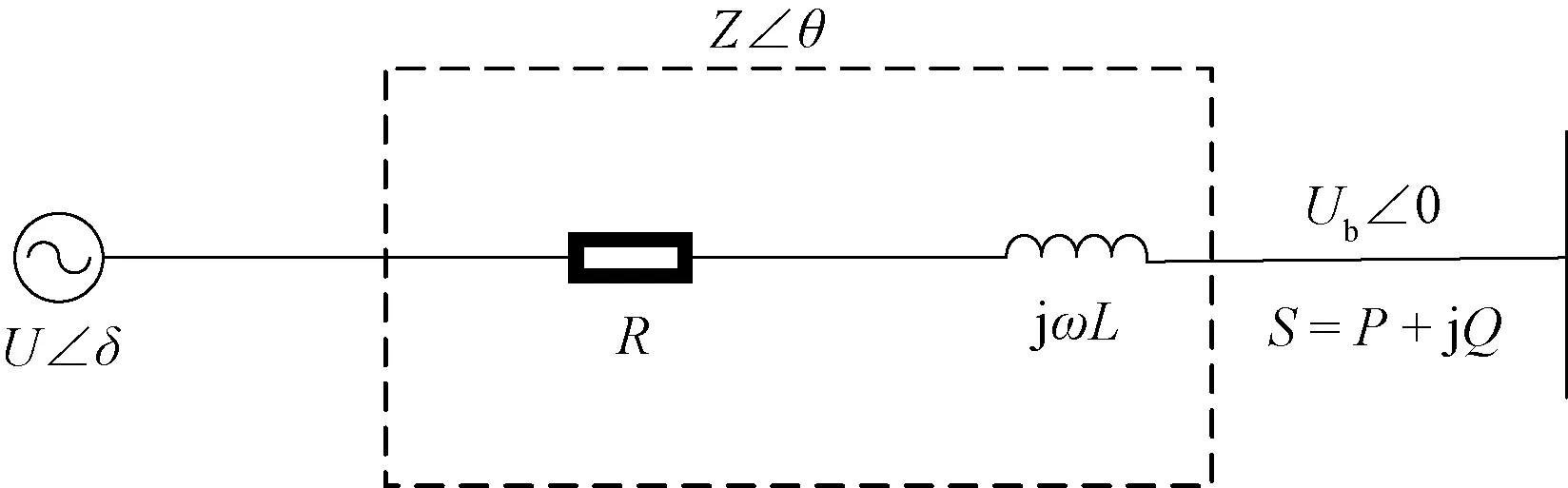
圖1 單臺分布式電源功率傳輸示意圖

由圖1可知，傳統的分布式電源通過線路阻抗R+jωL消耗部分有功、無功功率連接至母線上。當微電網中分布式電源到母線的輸出阻抗呈電感性狀態時，輸出的有功功率和無功功率如式(1)所示。

(1)

式中：U為輸出電壓幅值；X為阻抗幅值。

為研究線路阻抗在電感性條件下的功率分配問題，用頻率代替電壓功角δ，下垂控制表達式為

(2)

式中：Pref和Qref分別為下垂控制分布式電源輸出的有功功率和無功功率的參考值；P0和Q0分別為分布式電源的額定有功功率和無功功率；f0和U0分別為分布式電源的額定頻率和電壓；f和U分別為分布式電源的實測頻率和電壓；mf和nu分別為頻率-有功功率和電壓-無功功率的下垂系數。基于f-P和U-Q的下垂控制框圖如圖2所示。

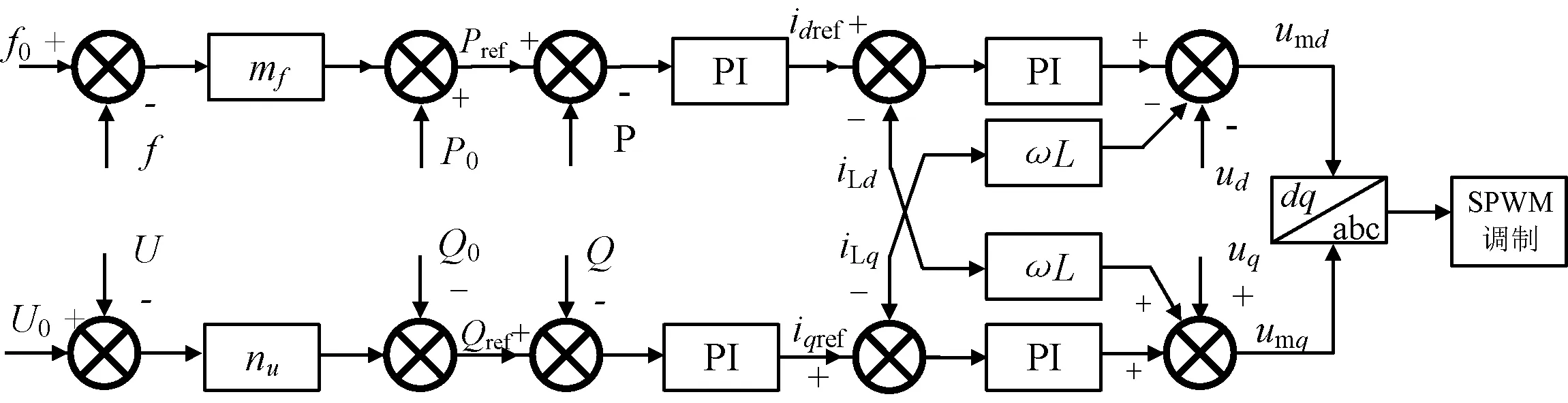
圖2 基于f-P和U-Q的下垂控制典型結構圖

由式(2)得出相應的頻率和電壓下垂曲線，如圖3所示。

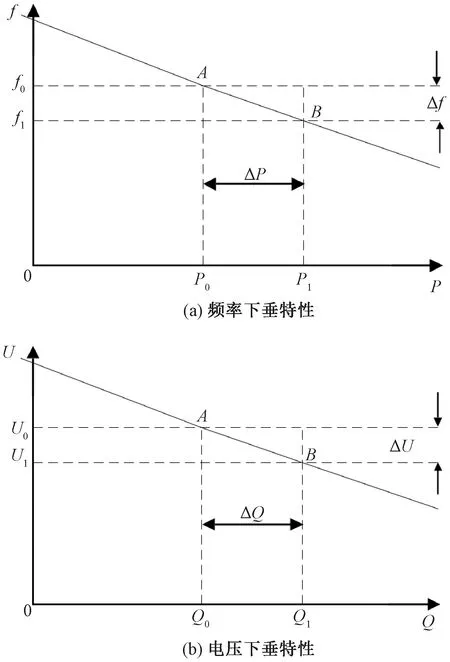
圖3 下垂特性示意圖

發電機功率的額定值根據視在功率確定，無功功率不平衡必然會引起發電機視在功率的不平衡，同樣會限制發電機組容量的發揮，特別是對于功率因數較低的電站，機組的帶負載能力不是取決于發電機的額定功率，而是發電機的額定電流。無功負載的不平衡也可以將其不均衡部分看成是兩臺發電機之間的一種環流，在發電機內部產生附加的損耗，甚至使發電機過載。

在傳統的下垂控制下，各分布式電源連接到母線上的線路阻抗不相等會造成無功功率分配不均，若有兩臺并聯的分布式電源，其容量相同但是線路阻抗Z1>Z2，則會出現如圖4表示的功率分配情況。由圖4可知，分布式電源的線路阻抗不等會造成無功功率分配不均，且線路阻抗越大，分布式電源無功功率越小。

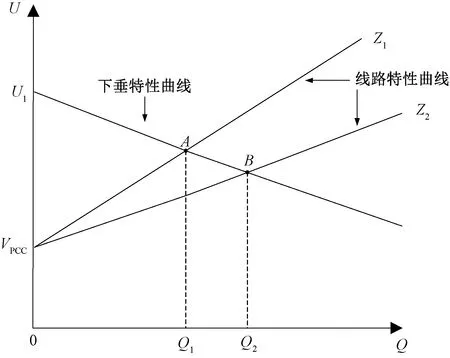
圖4 線路阻抗對無功功率分配的影響

2 分布式一致性理論在微電網中的應用

在分布式控制理論中，圖論通常起到載體的作用。一般情況下，用有向圖G=(V，E，A)表示由n個多智能個體組成的通信網絡；V={1,2,…,n}表示該圖中所有節點構成的集合；E?V×V表示各個節點相連邊；A=[aij]表示鄰接矩陣，若圖中的節點j向節點i存在連接則進行信息交互，aij≠0，反之，二者沒有連接不進行信息交互，aij=0；Ni={j∈V|(j,i)∈E}表示與節點i有信息交互的節點的集合。定義節點i的出度和入度分別為degout,degin，則有：

(3)

在微電網信息層內由通信網絡和多智能體構成的連通圖中，各節點相互連接的邊構成的拓撲結構顯得尤為重要，連接的邊數太少會導致系統的收斂速度變慢，連接的邊數過多將導致系統的通信成本增加，產生不必要的浪費。

出度元素在主對角線組成的矩陣為有向圖G的D矩陣，與信息交互相關的拉普拉斯矩陣L可表示為L(G)=L=D-A。若G中任意節點的出度值與入度值相等，則稱G為平衡圖，L滿足LI=0且ITL=0，其中I為n階單位列向量。若有向圖G每條邊都是雙向的，則(i,j)=(j,i)，即節點i與j可以互相通信，稱為無向圖，無向圖是平衡圖的一種形式；若有向圖G任一節點都可以找到一條路徑到達其他節點j，則稱為連通圖。

在微電網中可以將分布式電源抽象成多智能體的網絡節點，分布式電源彼此之間相互聯系。假設Qi為節點i的無功功率狀態變量，則可以得出以下控制策略：

(4)

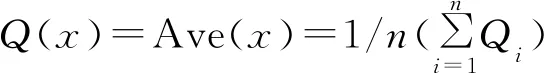
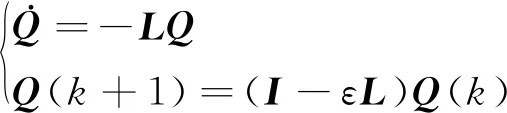
(5)

將一致性算法加入至微電網中的控制框圖，如圖5所示。

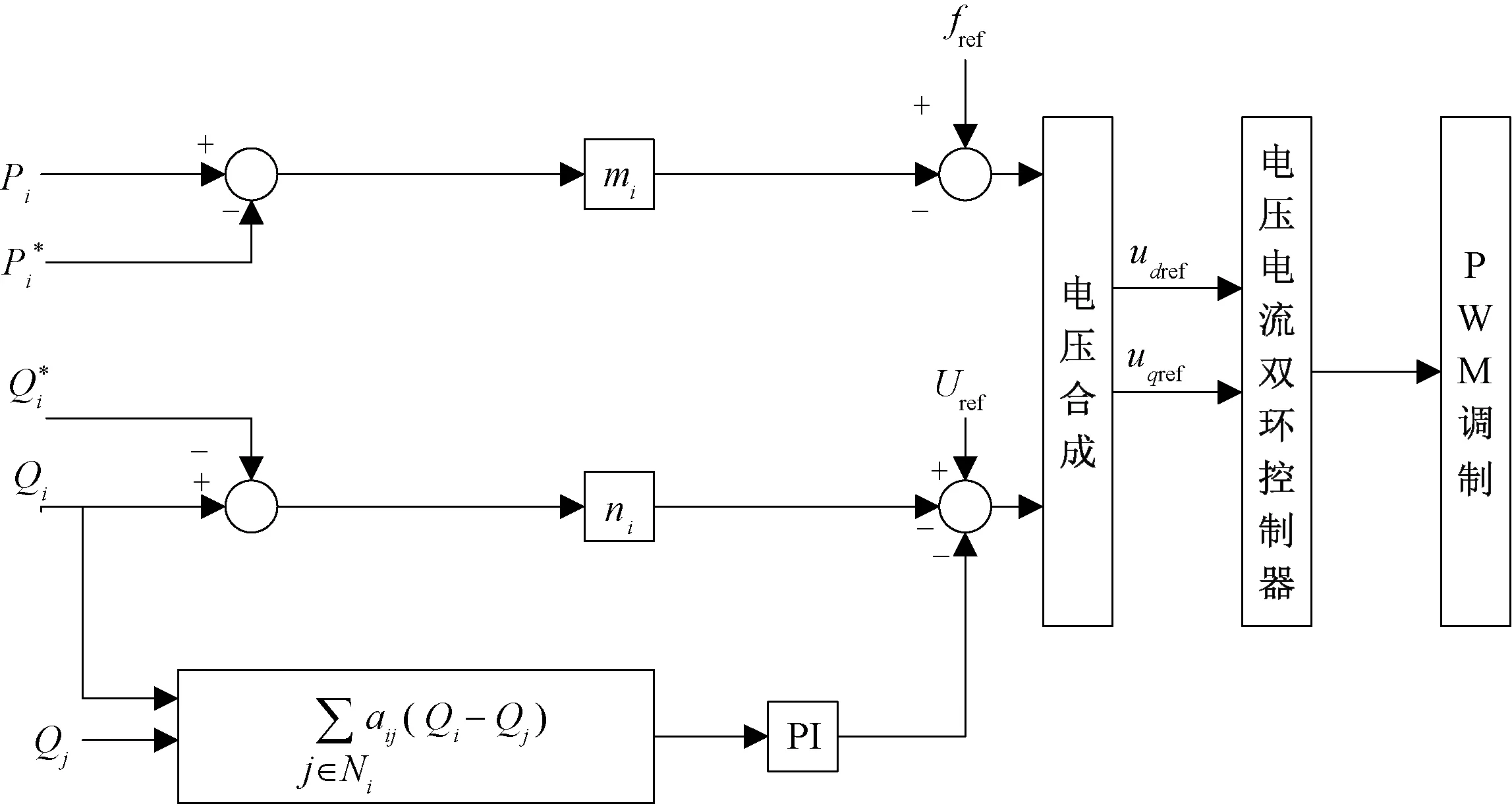
圖5 一致性算法應用于分布式微電網的控制框圖

加入一致性算法后微電網的無功功率分配示意圖如圖6所示，其中KP為原始的下垂曲線，KP1和KP2分別為經過一致性算法調整的兩臺分布式電源的下垂曲線，其中線路阻抗Z1>Z2。

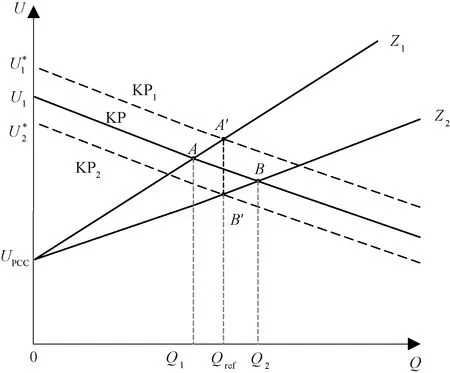
圖6 加入一致性算法后微電網的無功功率分配示意圖

對比圖4所示的下垂控制的無功功率分配可知，未加入一致性算法時，兩臺分布式電源的無功功率分別為Q1和Q2，沒有實現無功均分。加入一致性算法后兩者的無功功率(Qref)相等，實現了無功均分。

圖7描述了微電網的信息層和物理層，其中上層為微電網的信息層，信息層將微電網的分布式電源抽象成多個節點相連的網絡，其負責各個分布式電源之間的信息傳輸與傳遞。

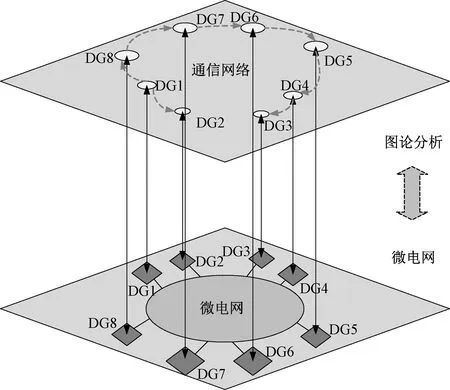
圖7 微電網圖論分析

系統的收斂速度與連通圖的拉普拉斯矩陣的第二小特征值相關，具體證明如下：

在一個無向連通圖G中建立拉普拉斯狀態不一致函數：

(6)

根據文獻[11-12]，網絡狀態不一致的相對收斂性有以下特性：

(7)

因為G為無向圖，所以rank(L)=n-1；根據Gerschgorin原理，L的n個特征值可以表示為0=λ1(L)<λ2(L)≤…≤λn(L)≤2Δ，Δ代表系統的最大出度，即Δ=maxidegout(vi),vi為分布式電源的出度。由式(6)可知，各個節點狀態不一致的收斂速度與拉普拉斯矩陣的代數連通度λ2(L)有關[13]，各個節點動態狀態為x=α1+η，其中α=Ave(x)對應于系統的穩定狀態，各個節點的最終狀態收斂于系統的平均值；η為狀態不一致向量，滿足1Tη=0，1=[1,1,…,1]T。在Lyapunov函數中V(η)=‖η‖2/2，可得式(8)。

(8)

3 最小通信鏈路模型與算法

分布式微電網拓撲結構優化的目標為：在原來拓撲結構的鏈路下，為減少通信成本，在代數連通度減小量最小的情況下尋找一種最小生成樹，即拓撲結構的連邊數最少。具體數學模型如式(9)所示。

(9)

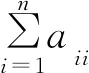
(10)

則λ2可表述以下推理：

(11)

式中：λ2(L1(μ))對應的單位右特征向量記為v2。

根據式(9)，λ2(L1(μ))對于μ的梯度為

(12)

由于L1=L-μLI是一個實對稱矩陣，則有如下推導：

(13)

因此有：

(14)

根據式(9)和(12)得出以下結果：

(15)

因此，希望刪除的邊權值μ造成代數連通度減小量Δλ2為最小，每次操作都會使得該拉普拉斯矩陣的第二小特征值減小量最小化，將上述刪除邊權值μ的過程進行循環，直至更新后的拓撲結構圖的代數連通度減小到0為止。提取上一次循環的連通圖作為更新的拓撲結構，根據以上推導及結論設計最小化通信鏈路算法。

最小化通信鏈路算法：

Step 1L=L(G),μ=0.1，i=0;

Step 2 whilei<10

L1′=L(G)-μLI,i++，L2′=L2′-L(G)

Step 3 Findmax{L2′(i,j),i≠j}

Step 4 刪除Step 3對應的邊，形成新的拓撲L=L1(G′)，代數連通度為λ2′

Step 5 ifλ2′>0,置L(G)=L1(G)

else 優化拓撲結構為L(G)。

為了檢驗該算法在普遍系統拓撲結構中的有效性，給出以下算例分析。隨機生成30個節點和93條鏈路的系統拓撲結構如圖8所示。

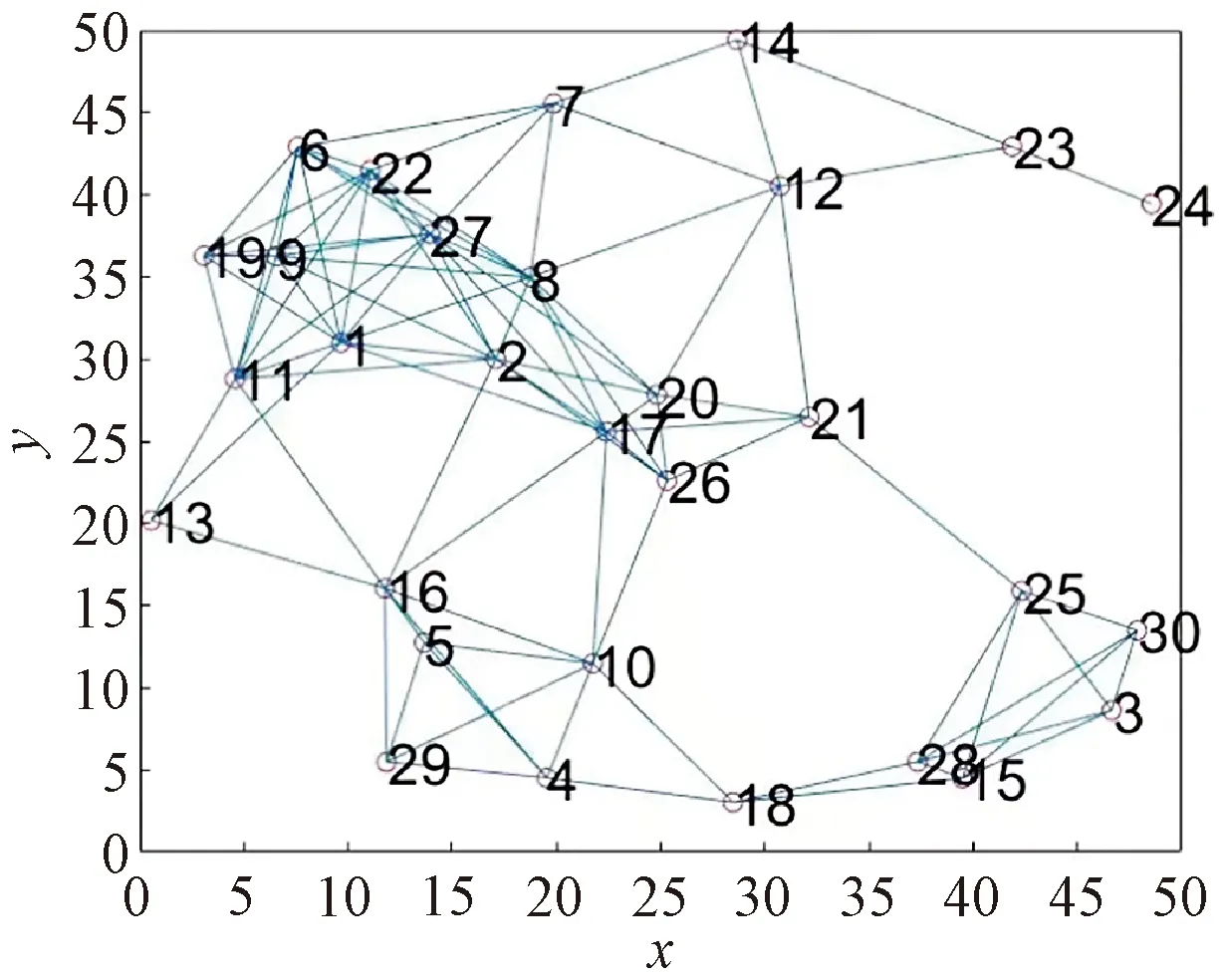
圖8 隨機生成的拓撲結構圖

經最小化通信鏈路算法刪除部分鏈路后的拓撲結構如圖9所示。優化后的拓撲結構共刪除64條鏈路，剩余鏈路為29條，為這30個節點的最小生成樹。

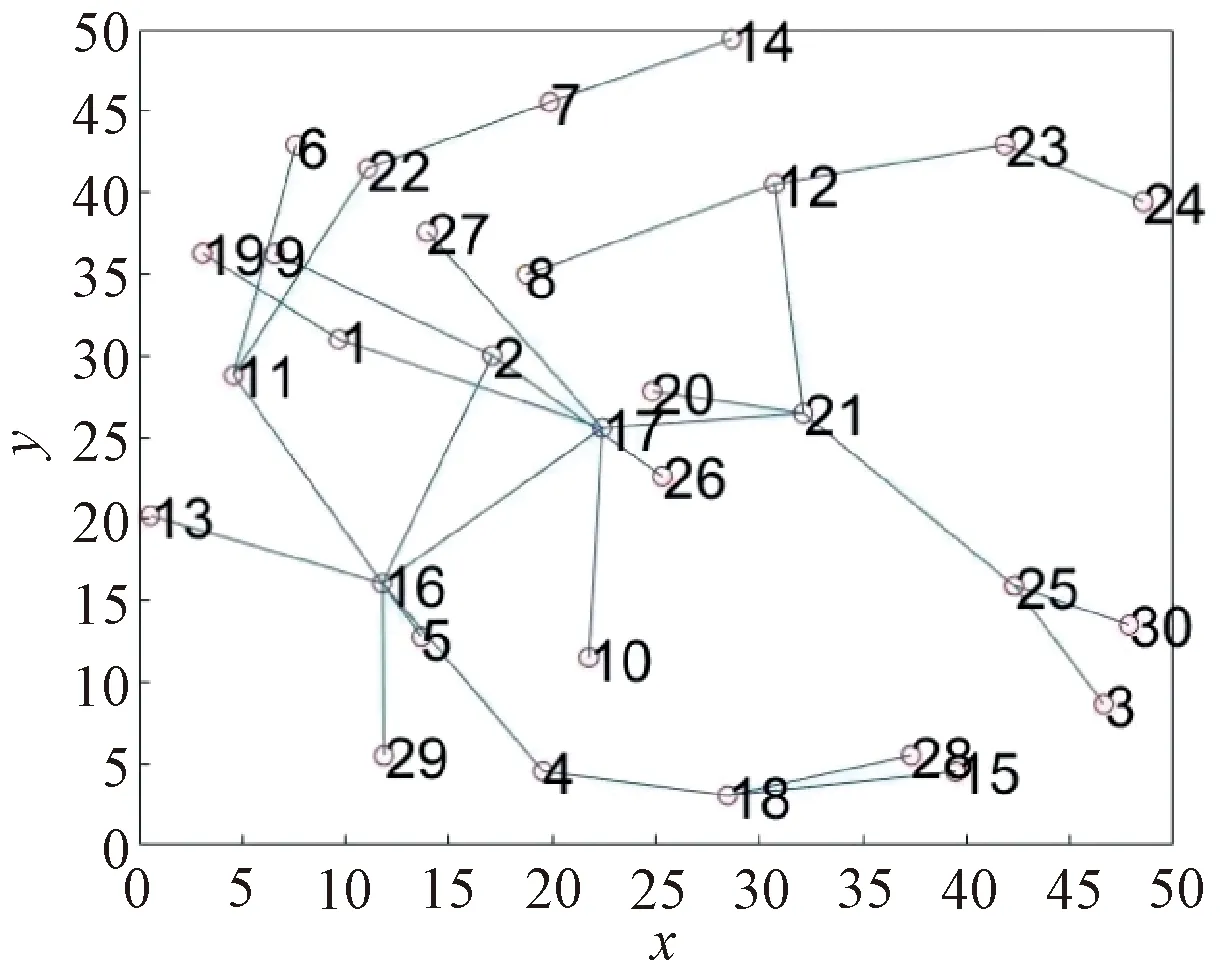
圖9 最小化通信鏈路后的拓撲結構圖

4 仿真試驗

為了驗證最小化通信鏈路優化算法的有效性，基于MATLAB/Simulink軟件環境搭建如圖10所示的微電網系統。在圖10所示的微電網系統中，5個相同容量的逆變型分布式電源DG1～DG5和兩個負載Zload1、Zload2連接在同一公共母線上，其中母線側電壓為750 V，微電網側電壓為380 V，有功-頻率下垂系數m=1×10-4Hz/kW,無功-電壓下垂系數n=3×10-3V/var,一致性算法的比例系數為0.2，積分系數為0.3，Pload1=6 kW，Qload1=5 kvar，Pload2=8 kW，Qload2=6 kvar。線路阻抗ZL1=(0.000 1+j0.002)Ω，ZL2=(0.000 2+j0.004)Ω，ZL3=(0.000 3+j0.006)Ω，ZL4=(0.000 4+j0.008)Ω，ZL5=(0.000 5+j0.010)Ω。

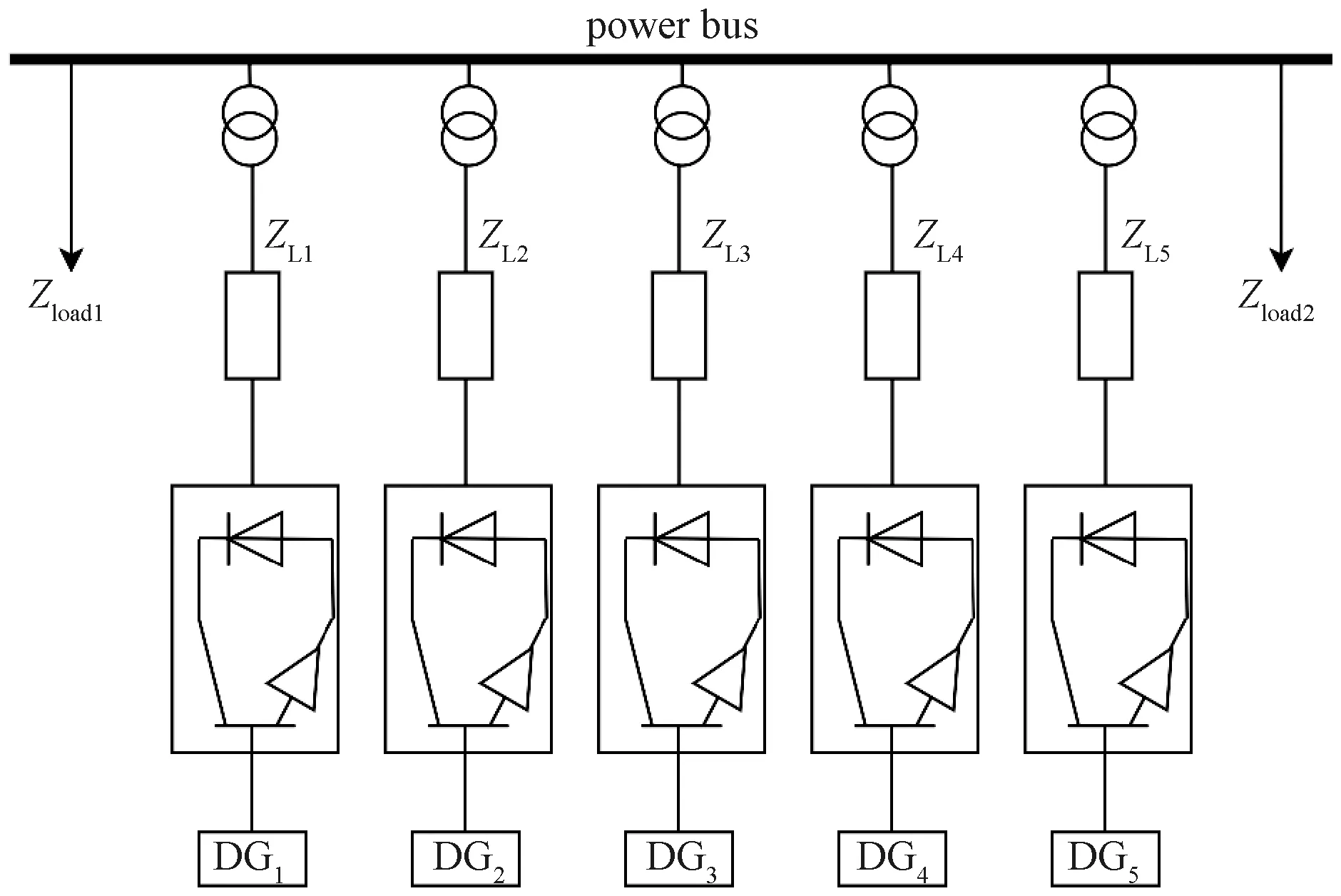
圖10 微電網系統結構圖

微電網的初始通信網絡拓撲結構以及經最小化通信鏈路算法優化后的拓撲結構如圖11所示。由圖11可知，代數連通度均為1，通信鏈路由6條減少為4條。由此可見，不僅代數連通度沒有減小，系統的收斂速度也與原來保持一致，并且通信成本在原來的基礎上降低了1/3。

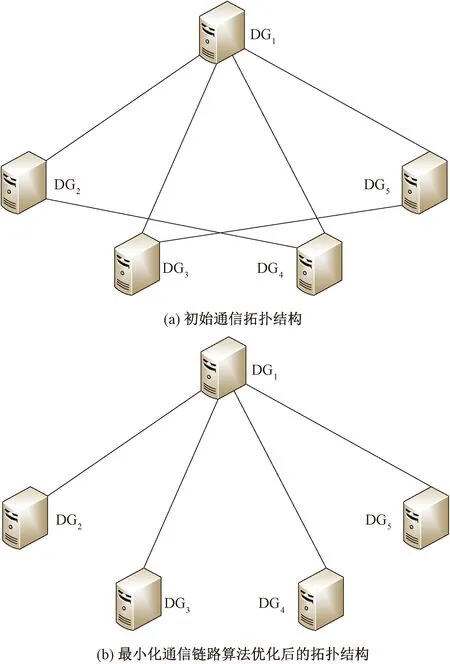
圖11 微電網通信網絡拓撲圖

微電網在0～0.3 s處于下垂控制，在0.3 s時加入一致性算法，各個分布式電源輸出的無功功率如圖12所示。由圖12可知，在優化后的拓撲結構的基礎上，無功功率在3.5 s左右實現了一致性收斂，完成了無功功率均分。

5 結 語

針對微電網中分布式電源間通信，研究拓撲結構影響收斂速度和通信成本的問題。根據圖論和分布式一致性理論的原理，在全連通圖的條件下使系統能夠達到收斂狀態；再根據靈敏度和梯度下降思想，設計了一種最小化通信鏈路算法，在系統的代數連通度減小量最小的前提下，刪除了部分通信鏈路，使得通信成本明顯降低。仿真結果表明，經最小化通信鏈路算法優化后的系統依然能夠實現無功功率均分，充分驗證了最小化通信鏈路算法的有效性。提出的算法在一定程度上證明了刪除通信拓撲結構的某些邊可以使代數連通度的影響趨于最小化，并且可以明顯降低通信成本。