基于無標度網絡的信用風險傳導模型

黃小莉，馮婉琪，吳蕾蕾

（1.西華大學電氣與電子信息學院,四川 成都 610039；2.弗里堡大學物理系,瑞士 弗里堡 1700）

隨著經濟建設進程的不斷深入推動，經濟的穩定增長成為我國經濟社會發展的重要目標。風險貫穿了金融工作業務往來的始終，如何利用技術創新更好防范風險是金融學者研究的重點，更是金融科技未來發展的趨勢。在防范金融風險方面，倪琦瑄[1]采用圖卷積算法聚合鄰居節點的屬性和連接信息，將復雜網絡的拓撲結構投影到低維向量空間，有效挖掘和保存了信貸用戶網絡的深層信息，提高了信貸風險預測準確性。陳君[2]通過弱化信息不對稱性和完善評估工具來完善信用評估體系，應用大數據進行信貸風險管理，建立了扁平化風險管理體系。李兆輝[3]利用神經網絡算法建立了評判決策的信貸風險量化分級模型，做出了信譽等級圖，可直觀讀出各企業信用等級。

由于現代金融體系具有高度市場化和風險分散性的特征，傳導性風險在企業之間傳播速度、強度以及范圍都不斷擴大加強。Allen 等[4]利用規則網絡進行仿真，得出完全結構的銀行間債務網絡受到流動性沖擊時更有穩定性的結論，對于債務網絡與風險傳染的研究具有開創性的意義。Thurner 等[5]利用星形網絡、隨機網絡、全連接網絡模擬債務傳染的過程。Gai 等[6]通過模擬隨機網絡上銀行債務傳遞，發現銀行破產數量隨著連接數量增加而減少。然而，隨著研究的深入，學者們發現包含銀行間債務網絡在內的企業間業務網絡并不是規則網絡或隨機網絡。Upper 等[7]和Craig 等[8]研究發現，在銀行間債務網絡中規模較小的銀行往往不會借錢給其他小銀行，而是更傾向于與其他規模大、信譽好的銀行進行往來。Boss 等[9]分析奧地利債務市場后也發現節點度服從冪律分布，即具有無標度特征。隋聰等[10]分析了中國銀行間數據，得出中國同業網絡具有無標度特性的結論。

在從復雜性研究的新視角探究傳導模型方面，Zhang 等[11]提出了一種考慮超級傳播機制的謠言和權威信息傳播模型，并將BA 無標度網絡[12-13]上的仿真結果與實際微博數據進行比較驗證。Zhu 等[14]結合時間與空間 2 種維度來探究謠言傳播的過程。Huang 等[15]深入研究了一類具有弱保護和強保護敏感節點的新型網絡傳染病模型。Ma 等[16]提出了一種新方法，實現精準識別單時延、多時延和分布式時延，并在實驗中揭示了空氣污染物作為疾病的原因。

由以上關于傳導性風險以及傳導模型的分析可知，在對信用風險的傳導研究時可從復雜性的視角切入。復雜網絡不僅研究各類網絡的靜態結構，還可以分析網絡的動力學特性，適用于分析謠言、輿論、疾病等的傳播過程。因此，本文從復雜網絡的動力學系統出發，提出一種基于無標度網絡的信用風險傳導動力學模型——NCAR（normal-credit risk occurred-affected-recovered from credit risk）模型。該模型更注重信用風險的內在傳導機制，并且考慮了各類干預措施對于模型的影響以及底層網絡的無標度特性，同時也考慮了由于風險沖擊導致企業破產和新企業成立的問題，這些都使得模型更符合實際情況。

1 信用風險傳導分析

1.1 企業間網絡結構分析

在企業構成的鏈接網絡中，將企業個體抽象為節點，企業之間的業務往來抽象為連邊。假定該網絡中有n家企業，在不考慮企業間業務往來的權重大小，只考慮是否存在業務的情況下，企業間的業務往來網絡可以用n階的鄰接矩陣來表示。

式中：ai j=1表示企業i與企業j之間存在業務往來；ai j=0表示企業i與企業j之間不存在業務往來。

網絡中企業的同質性是指企業個體之間高度無差異，不論是規模、聲譽、資產流動性等都相同。這種假設會更注重從宏觀角度討論市場發展規律，對于企業個體的作用考慮不足，并且在現實社會中也不可能存在有這樣的企業，因此，本文風險傳導模型的研究是基于企業具有異質性的。具有異質性的企業更傾向于與規模更大、聲譽更好、資產流動性更高的企業進行合作，這一點恰好符合無標度網絡中節點更傾向于鏈接度值較大節點的特征。無標度網絡由于節點個體異質性，使得節點之間連線數量的分布狀況存在差異，網絡中大部分節點只擁有少量連線，少量節點擁有大部分連線。本文提出的動力學模型就是基于無標度網絡的，網絡度分布滿足冪律分布。

1.2 經典傳染病模型

傳染病模型即是傳染病的基本數學模型。根據傳染病的各項參數建立的合理模型，可以更好研究傳染病的傳播速度、范圍以及內在傳播機制等，對于防治傳染病，管控其擴散傳播有著十分重要的意義。經典傳染病模型有SIS 模型[17]、SIR 模型[18]等。這2 類模型將人群分為了幾類：S（susceptible）類易感者、I（infected）類感染者和R（recovered）類恢復者。S 類指還未被感染疾病但有感染可能的人群；I 類指已經感染疾病且有傳播能力的人群；R 類指已感染疾病但恢復了健康并且有免疫能力的人群。

傳染病模型雖然最開始提出是為了刻畫傳染病在整個傳播過程中的擴散機制，但是現在已經廣泛用于輿情傳播、謠言演化、信息傳播等行業[19-21]，尤其是金融風險領域。從較為微觀的層面分析看，當金融風險在企業之間傳播的時候，其環境、對象和傳播機制都很類似于傳染病傳播。文獻[22 -24]指出金融風險的傳播非常類似疾病傳播。傳染病模型因在刻畫金融風險擴散傳導方面的優勢而不斷被擴展和創新，出現了SIRS模型、SEIR 模型等[25]。

1.3 NCAR 模型的建立

在發生系統性風險前，相關監管部門可以允許信用風險在各個經濟個體之間傳播擴散，財務狀況良好的企業能夠順利度過危機，而財務狀況本就存在問題的企業則會瀕臨破產，這一機制使得經濟個體在市場作用下自發進行優勝劣汰。然而相關監管部門的“不干預”政策也會在一定程度上導致社會經濟的劇烈波動，因此，面對較大范圍的風險蔓延和可能會發展成為系統性風險的情況，監管部門還是會采取一定的措施來進行市場干預。

典型的風險干預手段有2 種。一種是當某企業受到信用風險的傳導時，其他企業積極提供幫助，那么該企業的違約概率就會大大降低甚至不會產生違約行為，不會對網絡中的其他企業產生影響，該策略被稱為“救援策略”。第二種是受到信用風險傳導的企業主動切斷與其他企業的業務往來聯系，通過改善資本結構等措施來增強自身抵御風險傳染的能力，該策略被稱為“免疫策略”。

基于以上2 種策略，本文提出了NCAR 模型，流程圖如圖1 所示。

圖1 NCAR 模型流程圖

該信用風險傳導模型由4 類節點組成，分別為：

1）尚未發生信用風險的正常企業N（normal），該類企業自身財務狀況良好，但容易受到其他企業的信用風險傳導；

2）自身陷入信用風險危機的企業C（credit risk occurred），該類企業財務狀況較差，已經發生信用風險，且具備傳導風險的能力；

3）被傳導信用風險的企業A（affected），該類企業資本結構脆弱，抗風險能力較差，已被其他企業傳導信用風險；

4）已從信用風險中恢復的企業R（recovered from credit risk），該類企業經過各項干預手段，已經脫離了此次系統性風險。

信用風險傳導過程為：N 類企業因C 類企業的傳導以概率α1轉變為A 類企業，因A 類企業的傳導以概率α2轉變為A 類企業；A 類企業若也因自身原因陷入了信用風險，則以概率γ轉變為C 類企業；因為“救援策略”的干預，A 類企業和C 類企業分別以概率λ和μ轉化為N 類企業；因為“免疫策略”的干預，A 類企業和C 類企業則分別以β和δ的概率轉變為R 類企業。其中，ε表示N 類企業抵抗信用風險的能力，能力越低越容易被傳導風險，而θ1和θ2則分別表示了N 類企業受到C 類和A 類企業傳導的概率。模型中還考慮了新企業成立加入經濟網絡以及現有企業破產退出經濟網絡的情況，用概率η表示新企業的遷入率，用概率τ表示現有企業的遷出率。

令Nk(t)、Ck(t)、Ak(t)和Rk(t)分別表示t時刻在度值為k（k=1，2，3，···，n）的節點中各類企業的相對比例。根據平均場理論，可以得到NCAR 動力學方程，為：

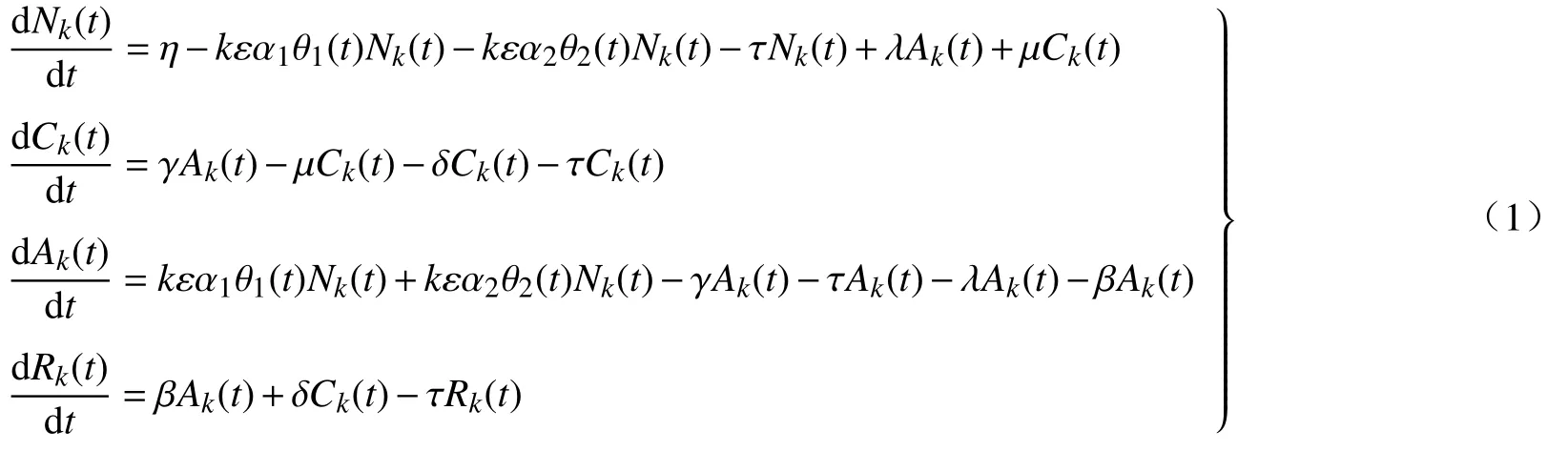
式中：θ1(t)代表在t時刻N 類企業與C 類企業之間存在信用風險傳導的概率，滿足

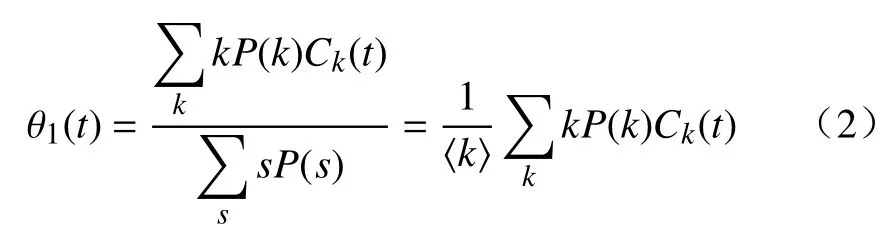
θ2(t)代表在t時刻N 類企業與A 類企業之間存在信用風險傳導的概率，滿足

因此，在t時刻，總站點數滿足

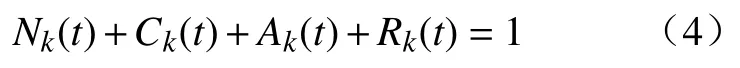
在t=0 初始時刻，4 種站點的比例應該滿足：

2 模型的平衡點分析

在傳染病模型中，基本再生數（basic reproductive rate）指一個病例在全部都是易感者的人群中直接造成的新感染者的平均人數。在本文NCAR 模型中，基本再生數指的就是一個陷入信用風險的企業在平均風險傳導期內所能傳播的企業數量。

令基本再生數為

則可以得到：

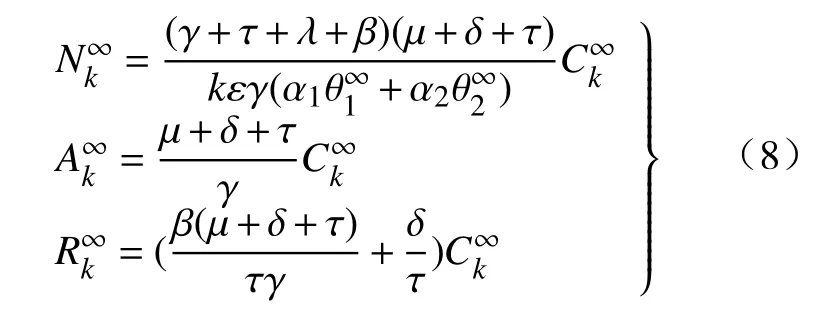
根據式（2）和式（3），可以計算出

根據Nk(t)+Ck(t)+Ak(t)+Rk(t)=1，可得到

將方程式（10）代入式（2），可得到

再將式（9）代入式（11），可得

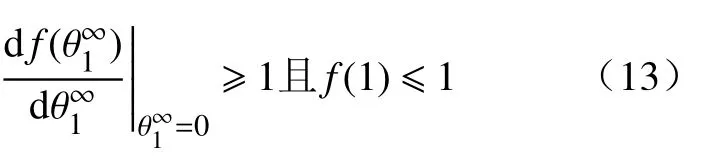
綜上所述，可以得到該系統中的閾值，即基本再生數為

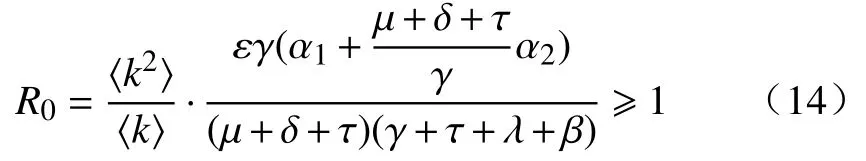
由此可知，當且僅當R0≥1 時，方程存在非平凡解。將非平凡解代入方程式（10），可得到，由方程式（8）得到：

由證明過程可知，系統的基本再生數R0受復雜網絡的拓撲結構影響，即復雜網絡關于平均度的參數〈k2〉/〈k〉越大，系統的基本再生數越大，即信用風險越容易在企業之間進行傳導。通過更改參數大小可以控制企業間信用風險的傳導范圍，這為制定措施控制風險，加強信用體系建設提供了新的解決思路。

3 信用風險傳導仿真結果

3.1 模擬風險傳導效應的結果

模型的仿真實驗均基于MATLAB 平臺。仿真實驗中，設置各類企業的初始狀態分別為：Nk(0)=0.4，Ck(0)=0.3，Ak(0)=0.3，Rk(0)=0。并且設定NCAR模型處于無標度網絡中，規模的大小為站點數S=1 000，平均度值 〈k〉=4，其度分布滿足P(k)=2m2k-3。

下列參數的設定均經過多次實驗調整，使各類企業比例變化曲線離散程度最大，仿真結果最好。

3.1.1 無干預手段下的仿真結果

在不采取措施干預風險傳導的情況中，選取參 數α1=0.8，α2=0.6，γ=0.2，β=0.1，δ=0.1，ε=0.1，λ=0.1，η=0.1，τ=0.1，μ=0.1，仿真結果如圖2 所示。

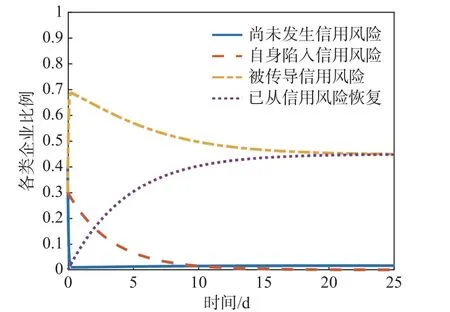
圖2 無干預手段下信用風險傳導過程

由圖2 可知，在沒有外力干預下，信用風險開始在企業之間傳導。尚未發生信用風險的企業在傳播開始后比例驟降，而被傳導信用的企業比例則迎來了激增。自身陷入信用風險的企業通過改善自身資產結構逐漸恢復了正常，比例逐漸減少。信用風險在前10 d 內迅速在企業之間傳播，比例最終在第20 d 達到穩定。這表明從第20 d 起，整個網絡中的風險傳導達到了一個穩定的狀態，此時基本再生數為

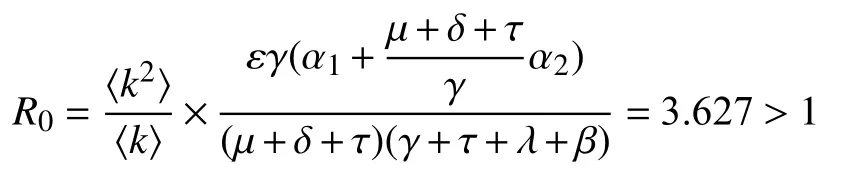
經濟網絡達到了信用風險持續傳導的平衡點，仿真結果與模型結論一致。

由圖1 可知，影響信用風險向外傳導的參數一共可分為2 類。1）由于救援策略的干預，企業間信用風險降低，但該類策略的實行取決于其他企業的救助，因此，被救援后的企業仍有可能被傳導新的風險，在這里就將救援策略抽象為了A、C 類企業轉化為N 類的概率λ和μ；2）免疫策略則是企業調整自身結構，提升抗風險能力從而避免信用風險傳導，因此A、C 類企業由概率β和δ轉化為R 類企業。下面就分別模擬這2 類策略干預下的信用風險傳導過程。

3.1.2 模擬救援策略干預下的風險傳導仿真結果

將救援策略的2 個參數分別設定為幾個不同值，保持其他參數不變的情況下，觀察被傳導信用風險的企業比例變化。仿真結果如圖3 所示。

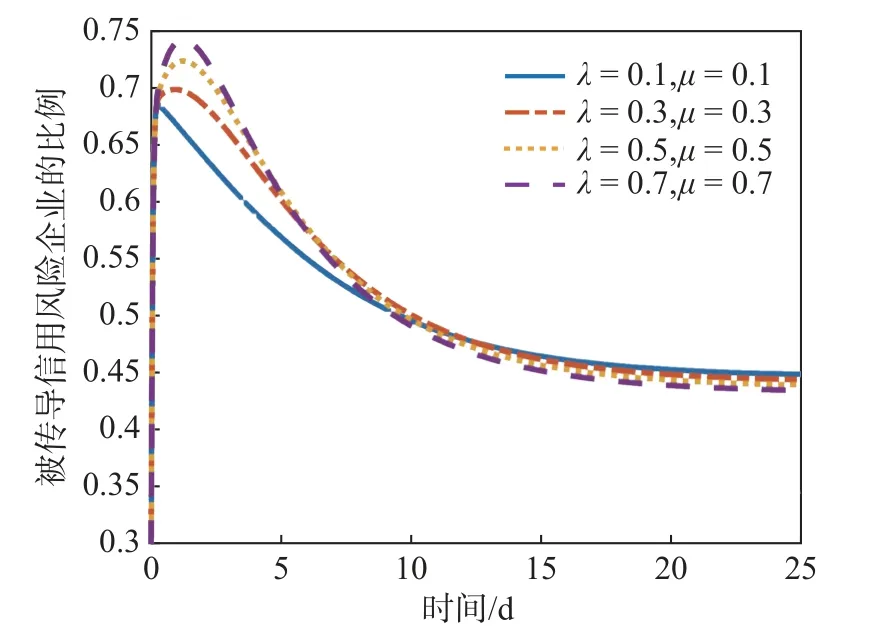
圖3 救援策略干預下信用風險傳導過程

由圖3 可知，當幾乎不采取措施（λ=0.1，μ=0.1）時，被傳導信用風險的企業在第20 d 時比例穩定在45.3%，而當相關部門采取一定救援措施后，受傳導企業的比例就會下降，即信用風險對經濟造成的損害也隨之降低，λ和μ值越大，受傳導企業的最終比例就越小。該結果表明，監管部門的救援策略會較為有效地降低企業受到信用風險波及的可能，同時，如果投入的救援成本越高，甚至可能直接達到無風險的穩定狀態，使整體經濟快速平穩發展。

3.1.3 模擬免疫策略干預下的風險傳導仿真結果

將免疫策略的2 個參數分別設定為幾個值，保持其他參數不變的情況下，觀察被傳導信用風險的企業比例變化。仿真結果如圖4 所示。

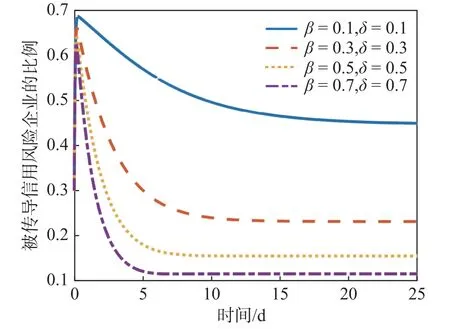
圖4 免疫策略干預下信用風險傳導過程

由圖4 可知，在不采取免疫措施（β=0.1，δ=0.1）的情況下，被傳導風險的企業比例在第23 d 時達到45%，而當監管部門采取免疫策略后，受傳導風險企業的比例顯著下降。如β=0.3，δ=0.3 時，在第10 d 就下降到了23%；當β=0.5，δ=0.5 時，在第9 d達到了15.6%；當β=0.7，δ=0.7 時，比例迅速下降，在第7 d 就降至11.6%。這表明，免疫措施力度越大，就可以越早遏制住風險的擴散。可見，當發生危險事件時，免疫策略比救援策略更為迅速有效，這為以后各項方案的制定提供了參考。

3.2 信用風險傳導模型的靈敏度分析

3.2.1 改變α1和α2的值

設定參數：γ=0.02，ε=0.1，λ=0.5，η=0.1，τ=0.1，μ=0.2，β=0.2，δ=0.5。逐漸增大α1和α2的值，觀察被傳導信用風險企業的比例變化情況。仿真結果如圖5 所示。

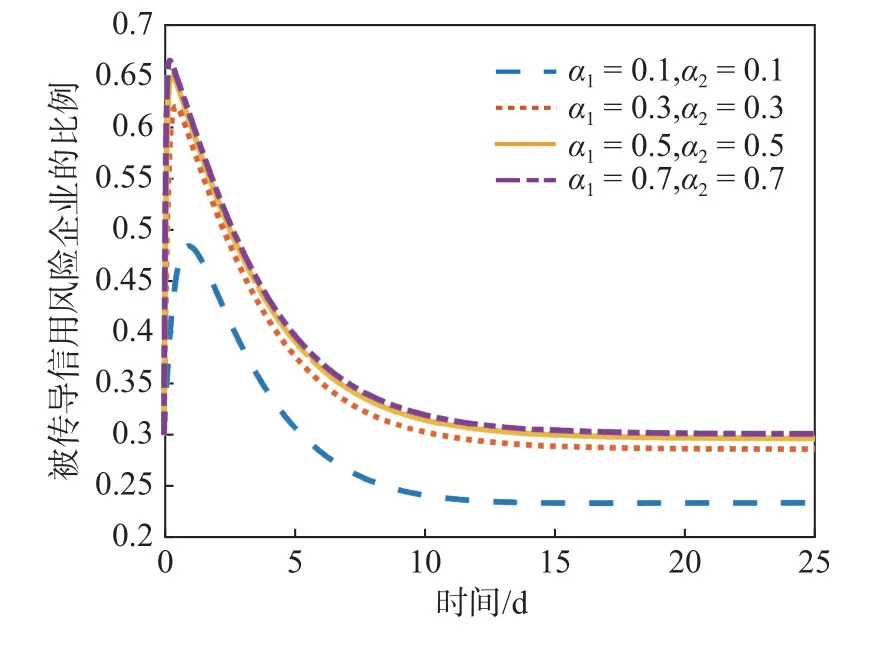
圖5 NCAR 模型對于α1 和α2 的靈敏度

由圖5 可知，被傳導風險的企業的比例會在開始傳導過程后迅速提高，在達到峰值后隨著時間緩慢下降。隨著α1和α2的逐漸增大，被傳導信用風險的企業的最終比例逐漸增高，此時的信用風險更具破壞性。當傳導能力較弱時（α1=0.1，α2=0.1），比例的峰值最低，且最終穩定在0.24。當傳導能力加強時，比例的峰值和最終值都會有較大的增長，但并不因為α1和α2的均勻變化而均衡改變。這代表整個傳導過程的影響因素很多，α1和α2值的影響也是有限的。

3.2.2 改變γ的值

設定參數：α1=0.1，α2=0.1，ε=0.1，λ=0.5，η=0.1，τ=0.1，μ=0.2，β=0.2，δ=0.5。改變γ的值，觀察被傳導信用風險的企業比例的變化。仿真結果如圖6所示。

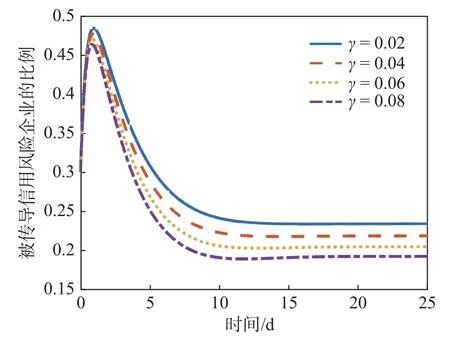
圖6 NCAR 模型對于γ 的靈敏度

由圖6 可知，當風險開始傳導后，被傳導風險企業的數量先會在第1 d 迎來快速增長，達到峰值后，數量逐漸減少，到第10 d 左右穩定在最終值。原因可能是企業通過自身的抵抗能力和各類干預措施恢復了正常業務往來擺脫了風險轉變為R 類企業，也有可能是因為企業自身陷入無法履行合同的危機轉變為了C 類企業。從圖中還可以看出，γ值越大，被傳導企業風險的數量下降得更快，且最終比例也最低，此時被傳導風險的企業更多地轉化為了C 類企業，即網絡中有了更多的風險傳導源頭，這時的經濟面臨著更大危機。

3.2.3 改變各類企業的初始值大小

設定參數：α1=0.1，α2=0.1，γ=0.02，ε=0.1，λ=0.5，η=0.1，τ=0.1，μ=0.2，β=0.2，δ=0.5。改變各類企業初始值大小，觀察被傳導風險企業的比例變化。仿真結果如圖7 所示。

圖7 NCAR 模型對于初始值大小的靈敏度

由圖7 可知：當C 類企業的初始值為0.1、0.3和0.5 時，被傳導風險企業的數量先迎來迅速增加，在第2 d 達到峰值后緩慢下降；當C 類企業的初始值為0.7 時，被傳導風險企業的數量會持續下降。無論初始值大小為多少，C 類企業的比例都會在第13 d 左右穩定在同一個值。這證明了初始值大小并不影響模型的演化過程，即風險開始傳導時，無論各類企業最開始數量為多少，只要企業抵抗風險能力和各類參與措施力度不變，最終達到穩定時的企業數量也保持不變。出現這種結果的原因是：觀察基本再生數的計算公式，其中不包含初始值大小，因此不管初始值如何改變，都不能加快或延遲模型的演化。這一點對于控制風險傳導的時間和范圍有一定借鑒意義。

3.2.4 改變度值的大小

設定參數：α1=0.1，α2=0.1，γ=0.02，ε=0.1，λ=0.5，η=0.1，τ=0.1，μ=0.2，β=0.2，δ=0.5。改變度值大小，觀察被傳導風險企業的比例變化。仿真結果如圖8所示。

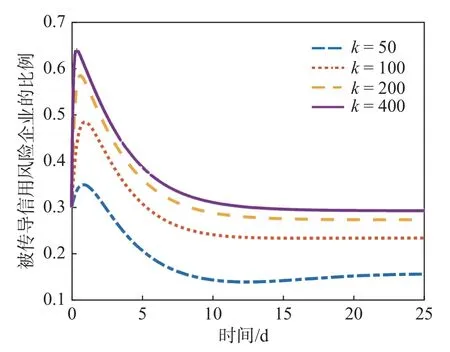
圖8 NCAR 模型對于度值大小的靈敏度

由圖8 可知，當度值增加時，即網絡模型內部關聯結構更復雜時，被傳導信用風險企業的比例峰值和穩定值更高。當度值為50 時，企業比例最終穩定在0.16 左右；當度值為100 時，企業比例最終穩定在0.24 左右；當度值為200 時，企業比例最終穩定在0.28 左右；為當度值為400 時，企業比例最終穩定在0.29 左右。這說明當一個企業度值越大，與其余企業的業務往來越頻繁，越容易受到信用風險的傳導。因此當已有企業陷入危機時，積極采取手段加強自身抵抗風險能力，盡快暫停與危機企業的業務合作非常重要。

4 結束語

本文根據平均場理論列出了信用風險傳導模型的動態方程，在計算出方程的基本再生數和平衡點后進行了仿真實驗。通過理論推導和仿真實驗可以得出，信用風險會在無標度網絡的傳導過程中逐漸收斂到穩定狀態。決定風險的穩定狀態是消失還是持續存在，就在于基本再生數的大小。當基本再生數大于等于1 時，信用風險將會持續影響經濟網絡，系統將會收斂至有風險的穩定狀態；當基本再生數小于1 時，市場會自發修復信用風險沖擊造成的失衡達到無風險穩定狀態。風險穩定水平所對應的被傳導企業比例，與表征救援策略的λ和μ呈負相關，與表征免疫策略的β和δ呈負相關，與表征傳導概率的α1和α2呈正相關，與轉化為自身陷入風險概率的γ呈負相關，與度值k呈正相關，與初始值大小無關。在多數情況下，監管部門的政策干預是必要的。如果任由危機蔓延，很可能引發整個體系的金融風險，在一定措施的干預下，危機蔓延的過程可以減緩甚至逆轉。從干預效果來看，免疫策略優于救援策略。