基于ARIMA-SVM模型的短時交通流量預測研究

陳 昆，曲大義，賈彥峰，王 韜，洪家樂

(青島理工大學 機械與汽車工程學院，青島 266525)

隨著社會經濟的高速發展，生活水平不斷提高，汽車擁有量顯著增加，截止到2019年底，國內的汽車數量約為2.615億輛，相比于2018年末增加了2122萬輛，其中私家車數量約為2.235億輛，增加了1905萬輛[1]。擁堵已經成為了城市交通狀況的常態，為了緩解這一問題，有的城市選擇在原有的道路條件下進行擴建，但其成本過高。從長遠來看應當利用智能交通系統對交通擁堵進行有效地疏通，其中交通流預測起著至關重要的作用[2-3]，能實時地為出行者提供有效的信息，有助于交通控制和交通誘導，提高通行效率[4]。當前在短時交通流量預測方面提出的方法包括：基于傳統統計分析方法的模型和基于現代化智能信息處理的模型。第一種包括：回歸分析預測[5]、時間序列的自回歸統計以及概率預測[6]等方法；第二種方法為非參數模型，其對復雜數據有較強的處理能力，能夠較好地提取交通流中的非線性特征[7]，如SVM模型(Support Vector Machines)。姚亞夫等[8]利用ARIMA模型(Auto-regressive Integrated Moving Average model)對交通流量進行預測，并證明了該方法的合理性。陳軍等[9]用SVM模型和BP模型(Back Propagation)分別對交通流量進行了預測，其結果表明了SVM模型在預測城市交通流量方面的優越性。蔣曉峰等[10]通過遺傳算法優化了SVM模型中的超參數，得到了良好的預測結果。

但上述的方法尚未考慮交通流的復雜性。從交通流的特征來看，在同一位置的交通流參數具有長期趨勢性，且通常認為預測的交通流量與歷史的交通流量數據存在一定的線性關系，但又因其交通的隨機波動性，導致交通流中亦存在非線性關系。ARIMA模型能夠準確處理交通流量中的線性特征，而SVM模型能夠捕捉其中的非線性特征，且具有魯棒性的優點，因此利用上述模型的組合形式能更好地預測交通流量并提高其預測準確性。本文將ARIMA與SVM組合起來，構建了ARIMA-SVM組合預測模型，并利用文獻[11]中西安市區道路的交通流量數據對模型進行仿真分析，且對比了ARIMA-SVM模型與ARIMA和SVM單一模型的預測精度。

1 交通流預測模型

1.1 ARIMA模型

ARIMA模型是在ARMA的基礎上將非平穩的時間序列經過差分處理為較為平穩的時間序列進行預測。交通流存在一定的周期性，使得交通流數據成為具有趨勢變化的一種時間序列[12]，因此對城市道路的短時交通流預測可以利用ARIMA模型。其公式為

(1)

式中：yt，yt-i分別為預測值和歷史交通流數據；μ為常數項；γi，θi分別為自相關系數和誤差項系數；p，q分別為自回歸階數和移動平均階數；εt，εt-i分別為模型的誤差和時間點i的偏差。

將預處理之后的西安市道路流量數據進行時間序列穩定性檢驗，通過ADF法檢驗其是否存在單位根。利用MATLAB數值仿真軟件中的ADF test()函數進行檢驗，當返回值為1時，即表示該交通流數據相對平穩；當返回值為0時，則認為其不平穩。將所得的交通流數據用函數檢驗得到的返回值為0，之后對數據進行一階差分處理，即差分次數d=1，重復上述操作，得到的返回值為1，表示序列平穩，即初步認定ARIMA(p,d,q)中得d值為1。

將經過一階差分后的交通流序列分別通過自相關系數ACF和偏相關系數PACF進行相關性檢驗，通過觀察相關函數圖，得到最優的p和q，取95%的置信區間。

通過圖1可以看出，在偏相關函數和自相關函數第4階出現截尾和衰減趨于0的現象，即確定q=4，p=4。

圖1 相關函數圖

通過觀察模型的正態性檢驗圖(圖2)，可知，其正態性檢驗基本呈線性分布，表示模型訓練效果好，因此確定最優模型為ARIMA(4，1，4)。利用交通流數據對模型進行仿真，其預測相對誤差如圖3所示。測試集前一部分數據相對誤差較小，之后出現了一定的波動，但整體來看預測效果良好。

圖2 正態性檢驗

1.2 SVM模型

SVM模型是基于結構風險最小化原理構建的，其預測模型函數表達式為

f(x)=w·φ(x)+b

(2)

式中：f(x)為預測函數；w為權重；φ(x)為非線性映射；b為偏置。

對于實際交通流問題存在許多影響因素，因此交通流數據一般為非線性[13]，可以利用核函數對非線性以及難以區分的數據的處理能力，將樣本從原低維的空間中通過核函數映射到高維空間加以區分，利用Lagrangian函數和對偶理論進行轉換，并按照KKT(Karush Kuhn Tucker)定理對已轉換的問題進行優化，其優化后的模型為

(3)

SVM模型常用的核函數包括線性核函數、徑向基核函數、多項式核函數以及多層感知器核函數等，核函數的選取對SVM模型的學習及泛化能力有重要影響。通過經驗選取適應度較好的徑向基核函數：

(4)

為了提高模型預測精度，將數據特征轉化為相同尺度，對所選用的交通流量進行數據歸一化，選取數據中的最值通過縮放將其歸一到[0,1]中，假設有M個樣本{x1,x2,x3,…,xm}，則

(5)

其中min(x)為M個樣本中的最小值，max(x)為M個樣本中的最大值，利用MATLAB數值仿真軟件對其進行訓練預測，并利用網格法尋找最佳的懲罰參數和核函數參數。

利用訓練集歸一化得到的數據對SVM模型進行訓練，并導入測試集中的數據進行模型仿真，其預測結果與真實交通流量的相關性分析如圖4所示。

判定系數R2的計算公式為

(6)

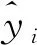
通常R2>0.75表示模型具有良好的擬合性和可解釋性；而R2<0.5，表示模型擬合效果較差。通過仿真可知SVM模型的R2=0.943，其值接近1，表示該模型的預測精度較高，能充分捕捉交通流中的非線性特征。

2 ARIMA-SVM組合預測模型

考慮到交通流容易受多種因素干擾，既存在線性交通流特征，也存在非線性交通流特征，因此本文采取ARIMA-SVM組合預測的方法對交通流進行預測，首先對交通流量數據進行預處理后，然后利用ARIMA與SVM分別對交通流數據進行預測，最后對各模型的預測結果進行加權組合[14]。依據各個模型在預測結果中的誤差大小來確定單一模型在組合模型中的權重，即在預測結果中的誤差越大，則在組合模型中所占權重越小。組合模型能減少對實際交通流量的預測誤差，提升預測精度，具體流程如圖5所示。

圖5 模型流程

>以組合模型預測誤差最小為原則，來確定最優權重組合。設

(7)

(8)

a+b=1

(9)

3 模型的數值仿真分析

3.1 數據來源與處理

對于短時交通流預測一般是指根據歷史數據對未來時間的交通流量進行預測，通常其時間粒度不超過15 min。本文將道路橫斷面交通檢測器15 min內檢測到的交通流量作為模型輸入，所用數據來自于西安市市區的交通流量[11]，數據采集技術為視頻采集，采集環境避開了大雨和大霧等不良天氣。因為工作日人們的外出更具規律，所以選取16個工作日交通流量數據用于模型的訓練和預測，采集時段為7：30—11：30，共288個數據。考慮到交通受外界因素影響時，如出現突發狀況或交通檢測器工作異常時，會導致數據的異常和丟失，將此類噪聲數據用于模型的訓練，會降低預測精度，因此，需要對異常的數據進行剔除，而丟失的數據使用前一天相同時間段的交通流數據進行補充。

數據集中共288個數據，前272個用于模型訓練，即訓練集，剩余的16個數據用于對模型的評價，即測試集。

3.2 評價指標

本文通過比較各模型的均方根誤差ERMSE，以及平均絕對百分比誤差EMAPE，可以得知訓練后的模型在短時交通流量預測上取得的效果。

(10)

(11)

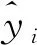
3.3 仿真結果

由于有多組預測值，因此權重確定函數以矩陣的形式表達，用MATALB數值仿真軟件建模求解。得a=0.453887，b=0.546113。由式(7)計算可以得到2個單一模型的組合模型：

(12)

對比各個模型預測結果以及交通流量的真實值，如圖6所示。

由圖6可知，建立的3個模型都有較好的預測效果，都能擬合出交通流的趨勢。就單一模型而言，交通流變化較大時，SVM模型相比于ARIMA模型能更好地捕捉交通流中復雜特征；交通流較為平穩時，ARIMA模型的預測效果更好。而組合模型兼顧了2個單一模型的優勢，從圖6中可以看出，在交通流平穩上升與下降階段，組合模型的預測曲線與實際值曲線幾乎重合；在其他階段的預測效果依然優于單一模型的預測效果。

從表1中各個模型的評價指標可知，組合模型的2個評價指標均低于ARIMA模型和SVM模型，證明了組合模型的預測效果更好，在面對較為復雜的交通情況時，仍然有較高的預測精度。

表1 模型預測評價

4 結論

建立了一種關于道路橫斷面交通流量的ARIMA-SVM組合預測模型，經過對3個模型的預測結果對比得知，ARIMA預測模型的EMAPE為4.17，SVM預測模型的EMAPE為3.69，ARIMA-SVM組合預測模型的EMAPE為1.57。組合模型的EMAPE和ERMSE均小于單一模型，由此可知，相比于ARIMA模型的線性預測以及SVM模型的非線性、高維度和小樣本數據預測，組合模型的預測結果要優于單一預測模型，該模型融合了2個單一模型的優勢，對復雜道路交通流的預測得到了較好的效果。