基于參數辨識的永磁同步電機矢量控制系統研究

于 震，唐 旭

(青島理工大學 信息與控制工程學院，青島 266525)

永磁同步電機(PMSM)具有結構簡單、效率高和節約能量等優點，而且近年來由于我國對稀土資源產業的重視使永磁同步電機的制造成本大幅降低，廣泛應用在交流伺服控制領域如工業機器人、新能源汽車等。目前以永磁同步電機為核心的交流伺服系統的控制部分通常以矢量控制為基礎，控制參數通常是由數學模型進行計算得到的，但在電機實際運行過程中，電機的定子電感、電阻和永磁體磁鏈等參數可能會受溫度、磁場飽和等影響發生變化，導致控制參數不夠精確[1]。隨著永磁同步電機的應用越來越廣泛，各個領域對交流伺服系統的精確度要求也越來越高，伺服系統必須實時獲得被控對象的精確參數才能滿足系統的要求。永磁同步電機的參數辨識主要有離線辨識和在線辨識兩種方法，只有在線辨識才能滿足現代高性能伺服系統的要求。目前常用的在線辨識方法主要有模型參考自適應法(MRAS)、最小二乘法、隨機梯度辨識法和人工智能辨識算法等等。模型參考自適應法具有算法相對簡單易于實現、穩態精確度高等優點，由SCHAUER于1989年首次將其應用于異步電動機的速度辨識，隨后又用于永磁同步電動機的無位置傳感器控制。它是根據自適應律使可調模型與參考模型的動態誤差收斂到零，使電機的待辨識參數逐漸收斂于實際參數[2]。MRAS的輸出可以是磁鏈、電感和電流等，通常應用于異步電機、勵磁同步電機的矢量控制和參數辨識[3]。

1 PMSM矢量控制原理

PMSM定子部分為三相繞組，轉子部分由永磁體材料構成，沒有勵磁繞組，是一個非線性、多變量、強耦合的復雜系統。假設定子繞組在空間上互差120°，結構為三相Y形對稱分布；忽略渦流、磁滯損耗和轉子的阻尼繞組；不計各線圈的電阻和電感變化。本文采用表貼式永磁同步電機，定子交直軸電感相等。矢量控制的基本思想是通過坐標變換將較復雜的交流電機模型等效成易于分析和控制的直流電機模型，把交流電流分解為勵磁電流分量和轉矩電流分量[4]。根據不同坐標系下的合成磁動勢相等的原則，經過Clark變換和Park變換，將永磁同步電機三相靜止坐標系的數學模型轉換為兩相同步旋轉坐標系的數學模型，如式(1)所示：

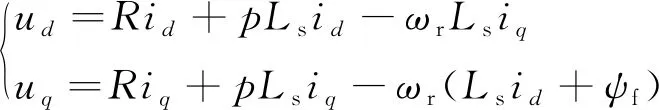
(1)

式中：ud和uq分別為定子電壓的d，q軸分量；id和iq分別為定子電流的d，q軸分量；R為定子電阻；Ls為電子電感；ψf為永磁體磁鏈；ωr為轉子角速度；p為微分算子。

磁鏈方程如式(2)所示：

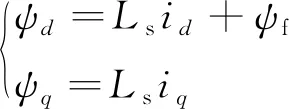
(2)

式中：ψd和ψq分別為d，q軸磁鏈。

矢量控制系統框圖如圖1所示[4]，由雙閉環調速系統模塊、坐標變換模塊、SVPWM逆變模塊和PMSM構成。電流環將三相電流通過坐標變換成d，q軸電流并分別與給定值做差作為電流調節器的輸

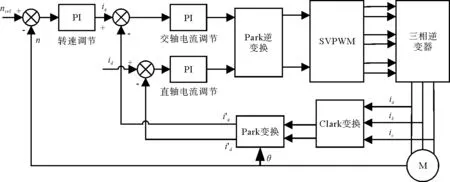
圖1 矢量控制系統

入，后經過Park逆變換得到兩相靜止坐標系下的電壓ud和uq，然后經過SVPWM運算得到逆變器的控制信號，以此來驅動永磁同步電機。控制定子電流id=0，此時q軸分量iq等于定子電流，控制iq即可控制電磁轉矩的大小，d軸電壓僅由iq控制，定子電流矢量分解為勵磁分量和轉矩分量，分別用于產生磁通和轉矩。兩個分量互相垂直且相互獨立，實現了定子電流兩個分量的解耦，控制簡單且效率高，可大大降低定子銅耗。

2 PMSM參數辨識系統

2.1 PMSM自適應參數辨識系統設計

采用模型參考自適應方法可對電機參數進行實時辨識。自適應參數辨識系統主要由參考模型、可調模型和參數自適應準則組成，系統框圖如圖2所示。MRAS的基本原理是給參考模型和可調模型相同的輸入量ud和uq，得到輸出量id和iq，計算輸出量的動態誤差e，經過自適應律調節直至差值逐漸收斂于零，并辨識出電機的定子電感、電阻和永磁體磁鏈參數[5-6]。

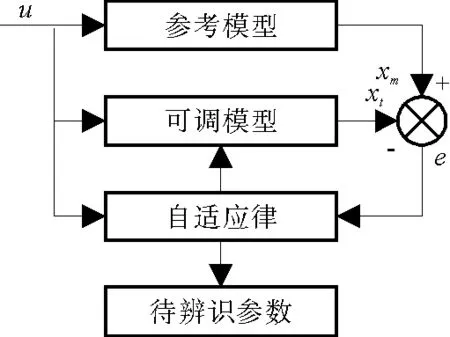
圖2 自適應系統

參考模型一般由基于電機定子電流的數學模型表示，如式(3)所示；可調模型如式(4)所示，用上標“^”表示可調參數。可調模型的參數由自適應律調節，且實際響應和參考模型相同。

(3)

(4)

2.2 基于Popov超穩定理論的參數辨識系統

Popov超穩定理論是參數辨識系統自適應律設計的基礎，這種方法能夠保證自適應律的準確性和穩定性，同時也易于實現。基本原理是將電機控制系統轉化為一個多變量非線性反饋系統，該系統包含線性定常前向回路G(s)和非線性反饋回路φ(s)。在一定條件下給定合適的輸入可使系統穩定[7]，如圖3所示。

圖3 非線性反饋系統

令r=0，u=-w，則前向回路狀態方程和輸出方程為

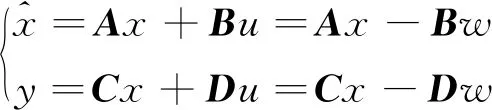
(5)

式中：x為狀態變量；u為輸入變量；y為輸出變量；A，B，C和D為系統參數矩陣，需滿足(A，B)完全可控，(A，C)完全可觀。

前饋回路的傳遞函數為

H(s)=D(sI-A)-1

(6)

反饋回路的輸出方程為

w=φ(y,t,τ),τ≤t

(7)

式中：τ為反饋回路和輸入變量之間存在的延時。

若使系統穩定需要滿足以下條件：

1) 反饋回路的輸入y和輸出w需滿足Popov積分不等式：

(8)

2) 線性前向回路的傳遞函數H(s)嚴格正實。將參考模型和可調模型的輸入為d，q軸的電壓ud和uq，輸出為d，q軸的電流id和iq，轉換為矩陣形式：

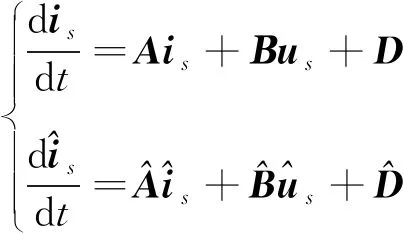
(9)

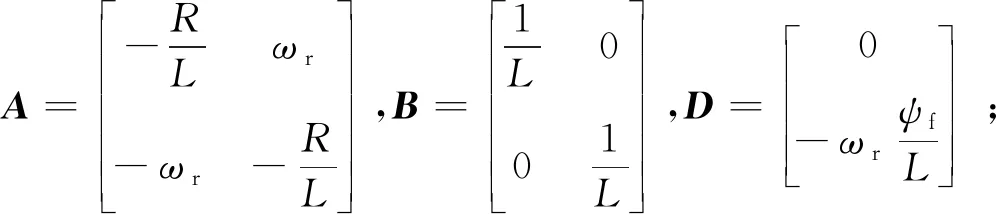
則誤差方程可表示為

(10)

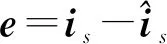
(11)

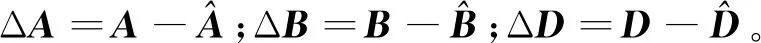
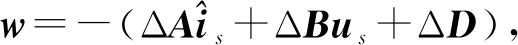
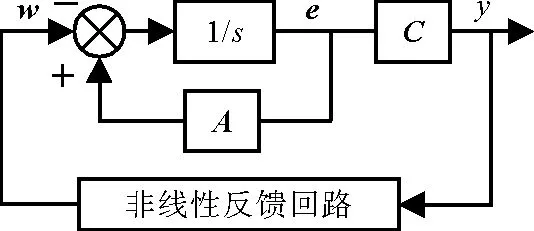
圖4 非線性時變反饋系統框圖

在非線性反饋回路中設計自適應律，使其滿足Popov積分不等式，將式(10)代入式(8)得到式(12)：

(12)

式(12)分解得到：

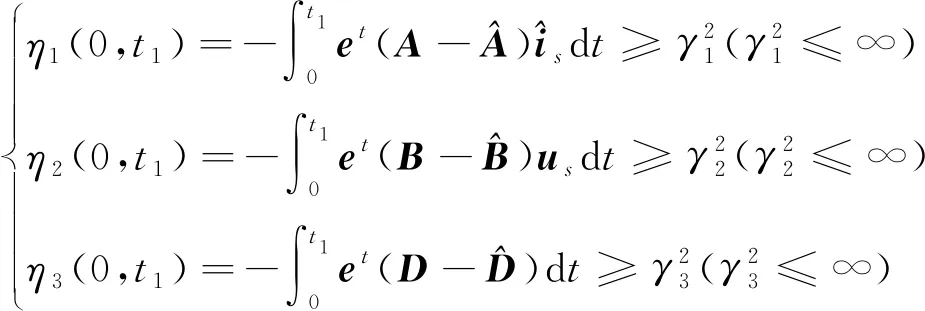
(13)

自適應規律為PI控制，得到自適應規律：

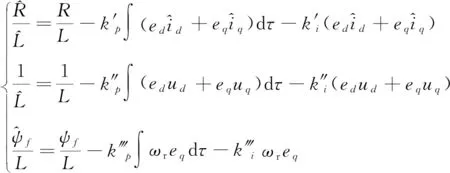
(14)

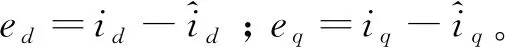
3 PMSM參數辨識系統仿真

參數辨識系統以PMSM矢量控制系統的MATLAB/Simulink仿真為基礎，加入基于MRAS的在線參數辨識系統仿真模型，可在線辨識定子電阻、定子電感和永磁體磁鏈。系統主要由永磁電機模塊、逆變器模塊、矢量變換模塊、PI模塊、SVPWM模塊和MRAS辨識模塊組成，仿真模型如圖5所示。MRAS模塊由可調模型和自適應律組成，仿真模型如圖6所示。給定永磁同步電機定子電阻0.958 Ω，定子電感8.5 mH，永磁體磁鏈0.1827 Wb，極對數為4；定子電阻、電感和永磁體磁鏈的初始值分別為真實值的50%，20%和400%；初始轉矩為10 N·m，經過0.2 s后轉矩增加到20 N·m，仿真時間為0.4 s，分析辨識算法在不同初始值情況下的辨識速度和精度。

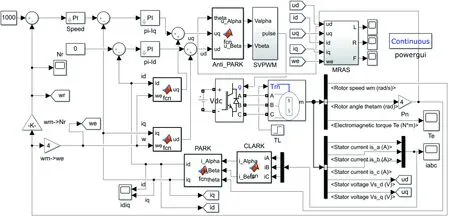
圖5 參數辨識系統仿真模型

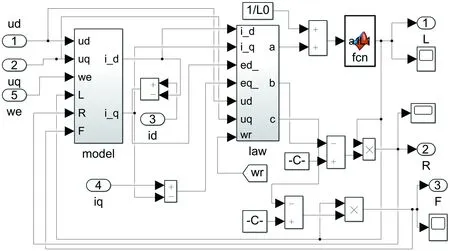
圖6 模型參考自適應系統

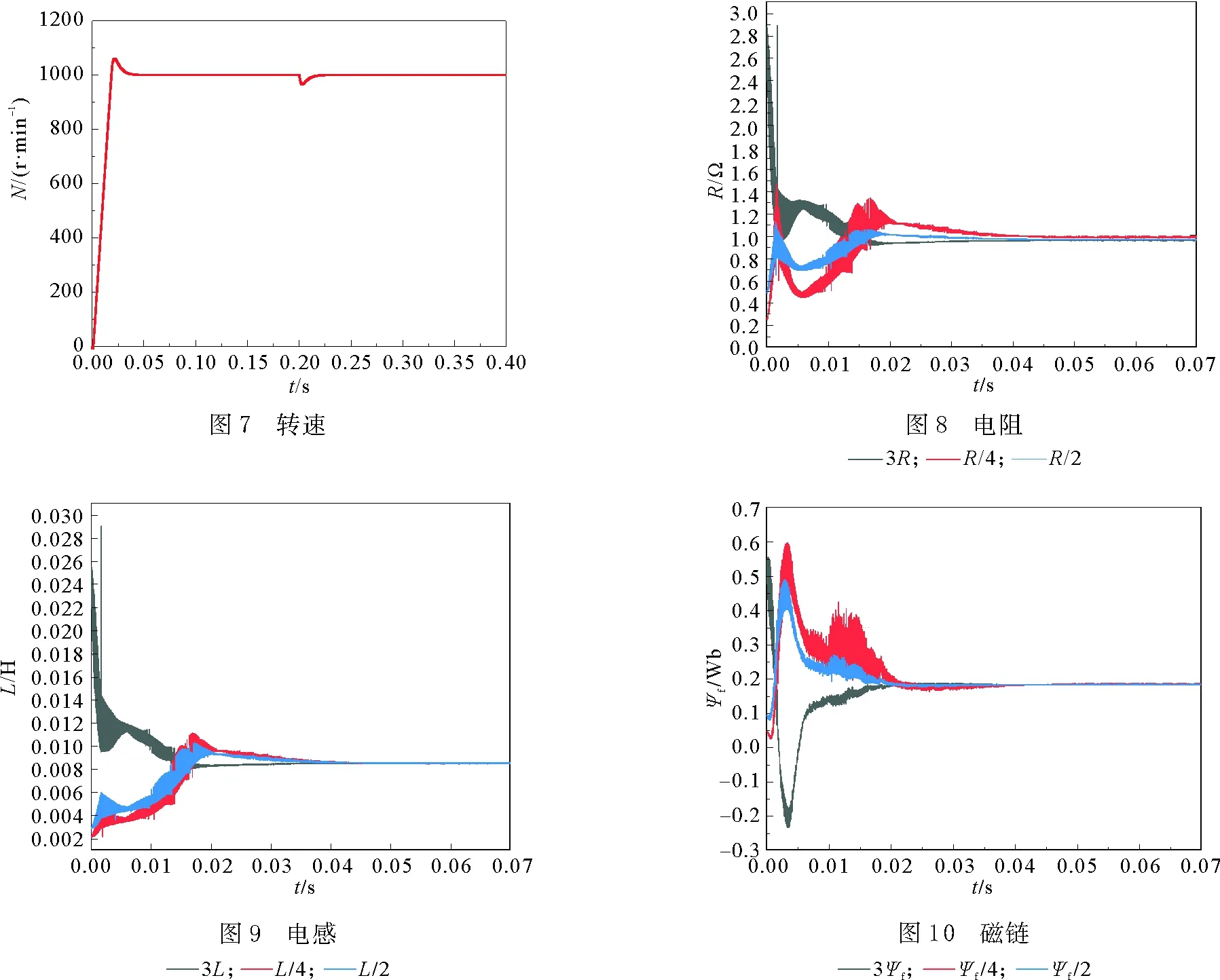
轉速結果如圖7所示，在0.02 s趨于穩定，在啟動和負載突然增加時有較小波動后立刻趨于穩定。為清晰顯示辨識方法仿真的結果，圖中只顯示0～0.1 s時間段的仿真結果，定子電阻、電感和磁鏈的識別結果如圖8—10所示。從圖8—10可以看出，電阻電感參數在0.03 s趨于穩定，永磁體磁鏈參數在0.02 s趨于穩定。辨識結果定子電感為8.499 mH，誤差為0.1%；定子電阻為0.964 Ω，誤差為0.6%；磁鏈為0.1825，誤差為0.1%。在不同初始條件下均能快速收斂，精度滿足矢量控制的要求。

4 結論

本文介紹了一種基于參數辨識的矢量控制系統。基于Popov穩定性理論的MRAS辨識算法可以保證系統的穩定性和收斂性。通過MATLAB/Simulink仿真驗證了系統的有效性。仿真結果表明，基于MRAS參數辨識的矢量控制系統對永磁同步電動機的起動、負載轉矩突變具有良好的適應性。定子電阻、電感和磁鏈辨識精度高，電機控制系統動態性能好，魯棒性強，能滿足各種高性能伺服控制場合要求。