砂土中吸力筒沉貫阻力模型試驗研究

任彥忠 趙學亮 李揚揚 隋淑環 宋啟明 游先輝

(1.華北電力大學，北京 102208；2.中廣核(福建)風力發電有限公司，福建 福州 350001；3.東南大學混凝土及預應力混凝土結構教育重點實驗室，江蘇 南京 211189；4.福建永福電力設計股份有限公司，福建 福州 350001)

1 研究背景

風能發電是世界上發展最快的可再生能源利用技術，海上風電場的建設以其優越的風能資源、日趨成熟的發電技術逐漸成為可再生清潔能源技術領域研究和開發的焦點。目前常用的海上風電機組基礎型式有單樁式、重力式、多樁式等。吸力式筒型基礎是近年來從深海基礎中逐漸發展起來的一種新型的海上風機基礎。相比傳統海風風機基礎，它具有施工安裝方便、方便拆除等優點，可替代復雜的嵌巖施工技術。

針對吸力式筒型基礎安裝阻力問題，國內外的學者們對此進行了系列相關研究。Allersma等[1]進行了砂土和黏土地基上的吸力式基礎離心機試驗，發現在砂土中吸力錨安裝方便，而且將沉箱土移出后測量發現箱內壁摩擦力起更多作用。Tran等[2-4]利用物理模型試驗和數值模擬的方法，探究吸力樁負壓沉放過程的土體孔壓變化規律，發現在臨界負壓狀態時沉放過程與孔壓發展關系密切。Gao等[5]在砂土地基上進行基礎安裝沉放和抗拔物理模型試驗，進一步分析了樁基礎安裝和抗拔特點。

理論計算與數值模擬方面，Houlsby和Byrne[6-7]通過簡化計算模型，建立了黏土和砂土條件中沉放阻力的公式，此分析過程中簡化處理比較多，需要使用詳細的地質分析資料，因此對地質勘察提出更多挑戰。Andersen等[8-9]通過分析黏性土和砂土地基中帶裙基礎、不同平臺不同荷載形式的錨，創新性地提出了沉貫阻力和承載力的計算方法。根據Andersen等的觀點，可以使用靜力觸探的方法計算砂土中裙板基礎貫入阻力。Dyson等[10]在鈣質砂土中使用離心機開展物理模型試驗，根據試驗結果，最終可以得到在不同安裝方法和不同加載速率條件下的修正因子。王胤等[11]在砂土中研究負壓沉貫過程中土塞的特征與機理，著重分析砂土滲透性，并將錨內砂土滲透系數的變化規律引入到 Houlsby 和 Byrne 理論模型中，對已有的吸力錨沉貫吸力理論模型進行了改進。

對吸力筒的安裝阻力，不同學者提出了不同的方法，本文對砂土中吸力筒沉貫安裝阻力進行了模型試驗研究，用于驗證對比不同計算方法的準確性。

2 試驗過程

參考已有研究結果可知，砂土中吸力筒沉貫阻力大小主要受內外側摩阻力大小影響，筒的直徑和沉貫深度是側摩阻力的重要影響因素，因此本試驗主要考慮不同直徑筒在沉貫過程中阻力的特性，筒長徑比的范圍由目前國內外研究結果與實際工程經驗確定，模型試驗參數及方案設計如表1所示，試驗中所使用砂土的物理參數如表2所示。

表1 模型試驗單樁尺寸

表2 試驗用砂物理參數

試驗過程包括自重下沉階段和負壓下沉階段，具體包括:第一階段，基礎在自重作用下沉入土中一定深度，1-R135,2-R170,3-R210自重下沉深度分別為10mm,19mm,14mm，最終達到穩定；第二階段，使用真空調節罐與真空泵逐級施加荷載，先使用真空泵抽吸負壓調節罐內部空氣，使得負壓調節罐內部達到預定的真空度，然后關閉真空泵，打開調節罐與試驗模型的連接閥路。待模型在穩定負壓的作用下下沉穩定后，關閉管路調節閥門，負壓逐漸消散。在負壓作用下基礎繼續下沉，當吸氣管中由氣體變為純凈的水流，說明由于負壓的存在，筒內水面上升，而繼續下沉后，吸氣管內出現明顯的砂子，說明筒頂已與土塞接觸，沉貫最終完成，吸力筒的安裝過程見圖1。

(a)自重下沉 (b)負壓沉貫下沉中期 (c)抽氣管出現水流 (d)抽氣管出現砂土

三組模型試驗在負壓沉貫結束后均產生了土塞，1-R135試驗工況土塞高度為86.2mm,2-R170試驗工況土塞高度為69.5mm,3-R210試驗工況土塞高度為69.1mm。可以發現，直徑越大的筒，土塞高度越低。實驗中土塞高度偏大，可能和加載方式有關。

3 試驗結果分析

3.1 負壓沉貫過程

將分級加載得到的三組負壓—沉貫深度曲線進行比較(見圖2),三個筒模型除了直徑不同，其余參數均相同，三個筒沉貫曲線差別較小，不過仍能發現相同負壓條件下，R=210mm的筒沉貫深度最，R=135mm的筒沉貫深度最小，沉貫所需負壓隨直徑的增大而有一定的減小趨勢。

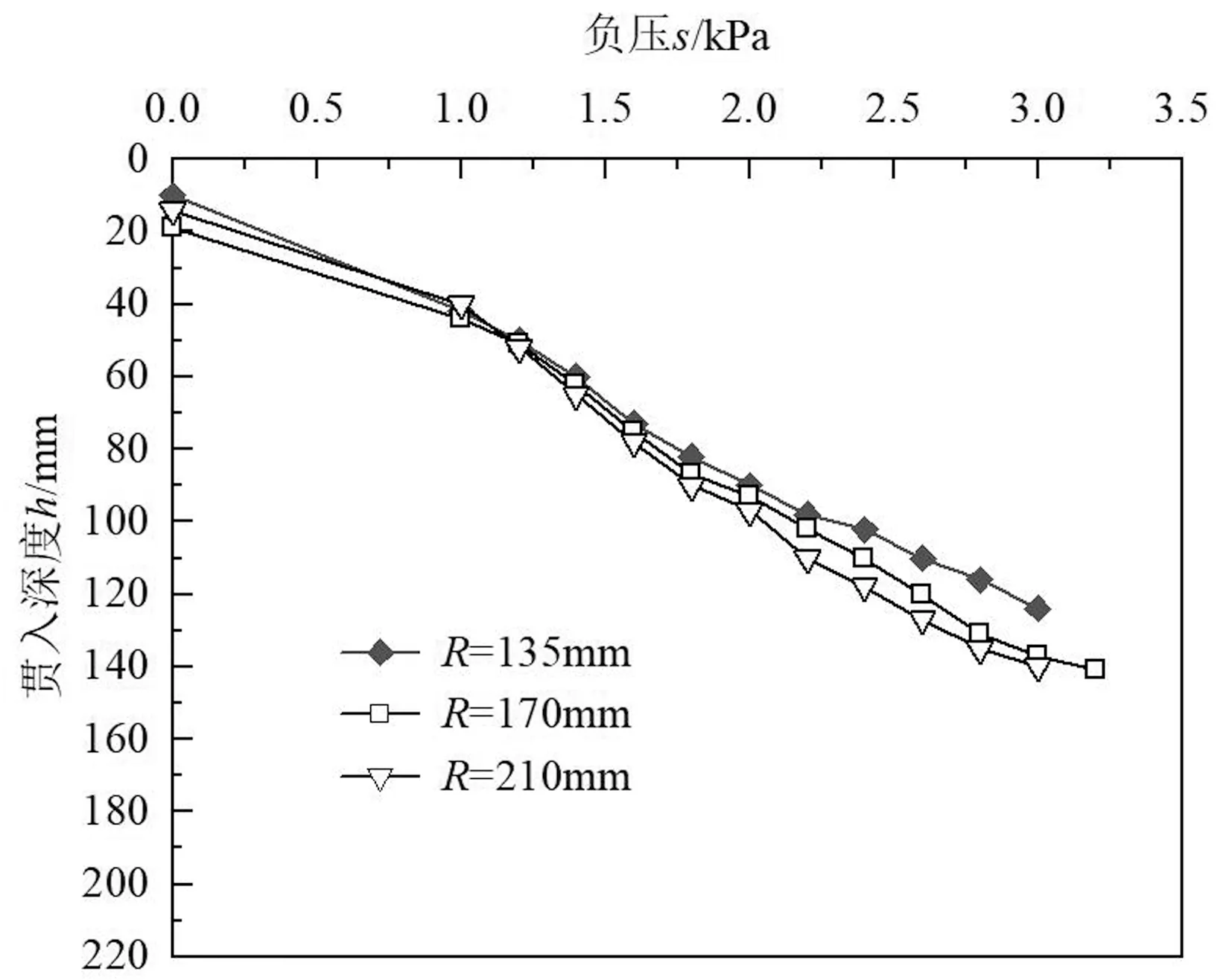
圖2 負壓—沉貫深度曲線

3.2 試驗結果與理論方法比較

計算砂土中沉貫阻力大小，比較常用的方法有Houlsby and Byrne理論方法、DNV規范推薦的基于CPT的方法，以及Senders和Randolph推薦的方法等。其中Houlsby & Byrne[7]推薦的計算方法如式(1)：

(1)

式中，V′代表樁自重；s代表安裝所需吸力；D代表樁徑(下標o和i分別表示樁外與樁內對應參數)；h代表吸力樁安裝深度；α代表粘結系數；t代表筒壁厚度；Zi為代表性參數，體現應力增強的范圍和土性。

該計算方法中所需參數如地基承載力系數Nq，Nγ在實際工程較難獲得，與砂土內摩擦角有關，本文中取值為30和52；地基承載力系數K在通過室內試驗結果和原位測試結果反推得到的值范圍在0.8～1.85，因此本實驗中選取K值等于1.1;吸力錨與砂土之間的摩擦角δ可參考Andersen的確認方法，選取摩擦角δ= 0.9φ。

DNV規范推薦基于CPT試驗所獲得的錐體阻力qc的計算方法如下：

R=Fi+Fo+Qtip

(2)

其中：

(3)

(4)

Qtip=Atipkpqc(L)

(5)

根據以往的工程經驗，錐體阻力qc隨深度變化qc=0.02+2616z。

DNV規范中，kf的建議范圍為0.001(最可能值)～0.003(預期的最高值)；對于kp是0.3(最可能值)～0.6(預期的最高值)，本文中，kf=0.002，kp=0.5。

DNV推薦方法未考慮滲流效應，Senders和Randolph[12]基于此提出了一種改進的計算方法，即:

(6)

其中scrit為臨界負壓，Senders和Randolph[12]利用有限元數值模型，建議臨界負壓計算方法如下:

(7)

為驗證這幾種計算方法的實用性和準確性，現將本文試驗中施加負壓與按Houlsby & Byrne理論解法、DNV推薦方法、Senders和Randolph理論解法計算沉放所需負壓進行比較。幾種方法的計算結果如圖3所示。

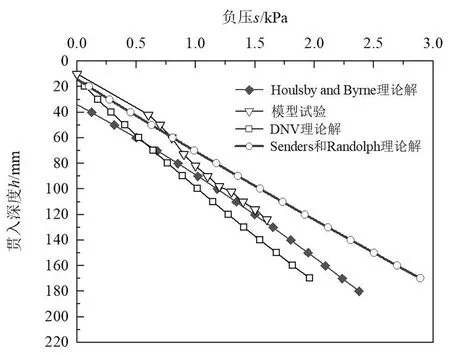
(a)R=135mm

(b)R=170mm

(c)R=210mm圖3 沉貫所需負壓對比

由圖3可以看出，在三組工況下，模型試驗結果均與Houlsby & Byrne法有較好的契合度，雖然負壓較小時理論計算得到所需負壓小于試驗結果，偏于保守，主要原因可能是Houlsby & Byrne的理論計算中，假設中筒內為理想滲流狀態，而模型試驗中由于尺寸效應等原因，導致在小負壓時，筒內滲流未充分發展。但當負壓增大至1.3kPa時，兩者趨向近似。

DNV法求得結果在相同沉貫深度時，所受到的沉貫阻力最小，其原因可能是擠土效應使得筒周圍土體應力水平提高，強度參數增大。由于筒壁的約束作用，內側土體的擠壓程度遠大于外部土體，而且筒壁內外側的側壁摩擦力也不同，基于CPT試驗的方法計算時沒有考慮內外側土壓力的不同，造成沉放阻力計算值較測量值偏小。同時，由于筒體內部土體的強烈擠壓和土塞效應，筒端土體也不可避免地受到擠壓，因此，DNV法筒端下沉阻力計算值可能偏小。

Senders和Randolph法相較于DNV法更接近于實際試驗結果，體現了其相較于DNV法考慮了滲流帶來的優異性，但其和DNV法均受筒徑影響較大，隨著筒徑增大，貫入同一深度所需負壓減小明顯，在實際運用時需考慮適用的筒徑范圍。

4 結論

通過吸力筒沉貫模型試驗，得到吸力筒負壓—沉貫深度曲線，并將結果與Houlsby & Byrne、DNV、Senders和Randolph推薦的方法所求得的理論解進行對比，發現Houlsby & Byrne方法最為接近試驗結果，不足之處在于小負壓情況下偏于保守，而隨著負壓增大至1.3kPa時，理論計算結果與試驗結果相近。而規范DNV推薦的方法求得的沉貫阻力偏小，Senders和Randolph法對其有改進，但受直徑影響波動較大。