基于耐震時程法的鋼筋混凝土框架彈塑性地震響應及損傷發展

張 超，周楨干，賴志超，黃 凱，朱 展，范小燕

（福州大學土木工程學院，福建福州 350108）

引言

準確預測、分析和掌握地震下結構的抗震響應，是判斷結構抗震設計合理性的重要依據之一。因此，完善結構的抗震設計和抗震評估方法至關重要。目前，基于性能抗震設計常用的評估方法有：彈塑性靜力分析方法（Pushover法）和增量動力分析方法（Incremental Dynamic Analysis，IDA）等［1-2］。Pushover法是非線性靜力的分析方法，不能很好的考慮地震動的隨機性和結構的動力效應［3］。IDA法可以反映結構在不同地震動作用下的動態特性，但缺點是需要進行大量的時程分析，計算繁重，十分耗時，且較依賴于地震波的選取。基于此，ESTEKANCHI等［4］發展了一種新的結構抗震分析方法-耐震時程法（Endurance Time Method，ETA）。其綜合了IDA法的動力效應和Pushover法的簡便快捷，達到了計算精度和效率的折中。因此，在結構抗震評估領域中有非常廣闊的應用前景［5］。

為了探討ETA方法在地震失效模式評估方面的可行性，本文在研究耐震時程曲線的擬合方法基礎上，以鋼筋混凝土框架為研究對象，應用ETA方法分析了鋼筋混凝土框架的地震響應及損傷發展。

1 耐震時程法（ETA）與時程曲線（ETEFs）擬合思路

1.1 耐震時程法（ETA）的基本思路

耐震時程（ETA）法是通過對結構施加一條或一組預先設計的強度指標隨時間不斷增大的耐震時程激勵函數（Endurance Time Excitation Functions，ETEFs）曲線，即耐震時程加速度曲線，作為地震動輸入。并根據結構能否滿足預先定義的性能指標的耐震時間t來判斷結構的性能。將一組ETEFs曲線施加到不同的結構，當達到相同的性能指標時，其所經受的耐震時間tE不一樣。對指定的一個結構而言，達到不同的性能指標，所經受的耐震時間tE也不一樣。因此，ETEFs法是根據結構能夠承受ETEFs曲線的耐震時間tE來評估結構的抗震性能的好壞。

進行耐震時程分析的關鍵在于合成分析過程中所需輸入的ETEFs曲線。該ETEFs曲線最典型的特性是：隨著耐震時間tE的增大，峰值加速度也不斷增大，且ETEFs曲線的任一時段內，其目標加速度反應譜與耐震時間成線性比例關系。為了保持ETEFs曲線的這一特性，需要在ETEFs曲線擬合過程中設置一定的約束條件。

式中：t為時間變量；tTarget為指定的目標時間點；T為結構的自振周期；Sac（T）為預先指定的總目標加速度反應譜；SaT（T，t）為0～t時段內的目標加速度反應譜。

由式（1）可知：tTarget和tTotal決定了分時段目標反應譜與總目標譜的縮放系數，從而影響了耐震時程曲線在耐震總時長內所能達到的加速度峰值。當總目標譜Sac（T）相同時，tTotal/tTarget的比值越大，耐震時程曲線的峰值加速度越大。

耐震加速度時程的目標位移反應譜可與目標加速度反應譜緊密聯系，表示為：

式中：SuT（T，t）為0～t時間段的標位移反應譜。

ETEFs曲線的合成是通過對位移反應譜與加速度反應譜的線性約束，但很難在每一時刻都同時滿足式（1）的要求。因此可將其轉化成無約束變量的優化的問題：

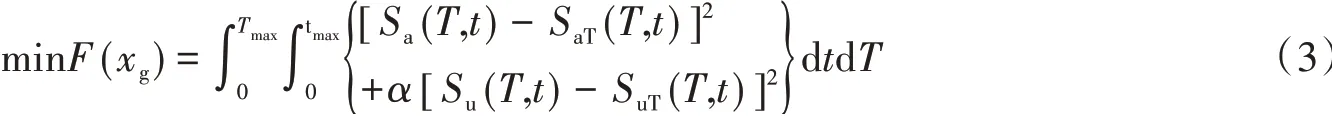
式中：xg是需合成的耐震時程加速度曲線；Sa（T，t）和Su（T，t）分別為耐震時程曲線上0～t時段內的加速度反應譜和位移反應譜值；α是加速度和位移函數的相對誤差的權重系數。本文的強度指標采用的是加速度反應譜，因此位移譜權重系數α取值為0。

通過耐震時程法所獲得的的的地震響應結果是往復的，因為其本質上是一種時程分析，并且可以通過以下方法獲得結構在不同強度下的工程需求參數（EDP）：

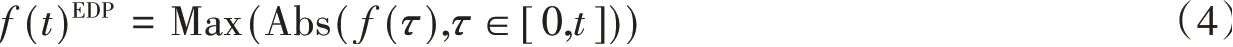
式中：f（t）EDP為t時刻時結構在耐震時間的工程需求參數；f（τ）為結構在［0，t］時間段內結構的響應時程。

該方法的分析結果可以這樣表示：橫坐標以t為參數，也代表地震動的強度（Intensity Measure，IM）；縱坐標為工程需求參數f（t）EDP，即表示在不同強度地震動作用下，結構響應的最大值。

1.2 耐震時程曲線（ETEFs）的擬合思路

基于耐震時程曲線的特性，確定出ETEFs曲線的擬合目標：首先，目標ETEFs曲線需要滿足加速度隨著耐震時間tE的增大而不斷增強的特性。同時，還要求不同時間段內的ETEFs曲線的加速度反應譜應與分時段目標反應譜最大程度吻合。本文確定出ETEFs曲線擬合的流程，如圖1所示。并基于MATLAB平臺編制了ETEFs曲線自動擬合程序。

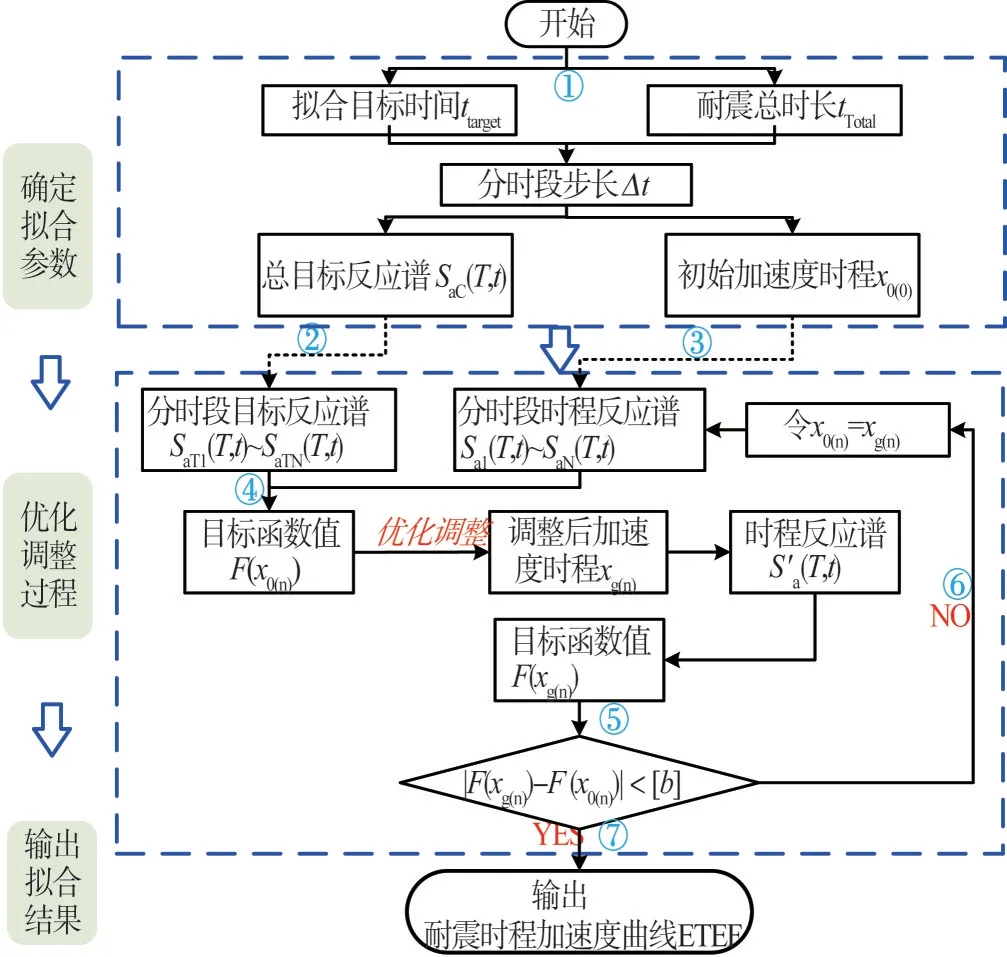
圖1 ETEFs時程擬合流程圖Fig.1 Fitting flow chart of ETEFs time-history

2 基于ETA方法的SDOF體系地震響應

2.1 耐震時程曲線擬合

該算例選取的總目標加速度反應譜如圖2（b）所示。算例其它擬合參數如下：目標時間tTarget=10 s，耐震總時長tTotal=30 s，時段步長Δt=1 s。根據總目標加速度反應譜求得所有30個分時段目標加速度反應譜，如圖2（a）所示。圖中：0～1 s的目標反應譜是總目標譜的0.1倍；0～30 s的目標反應譜為總目標譜的3倍。為了減少后期迭代調整的計算量，本文選用與耐震時程曲線比較一致的加速度時程作為初始加速度時程x0，如圖2（b）所示。

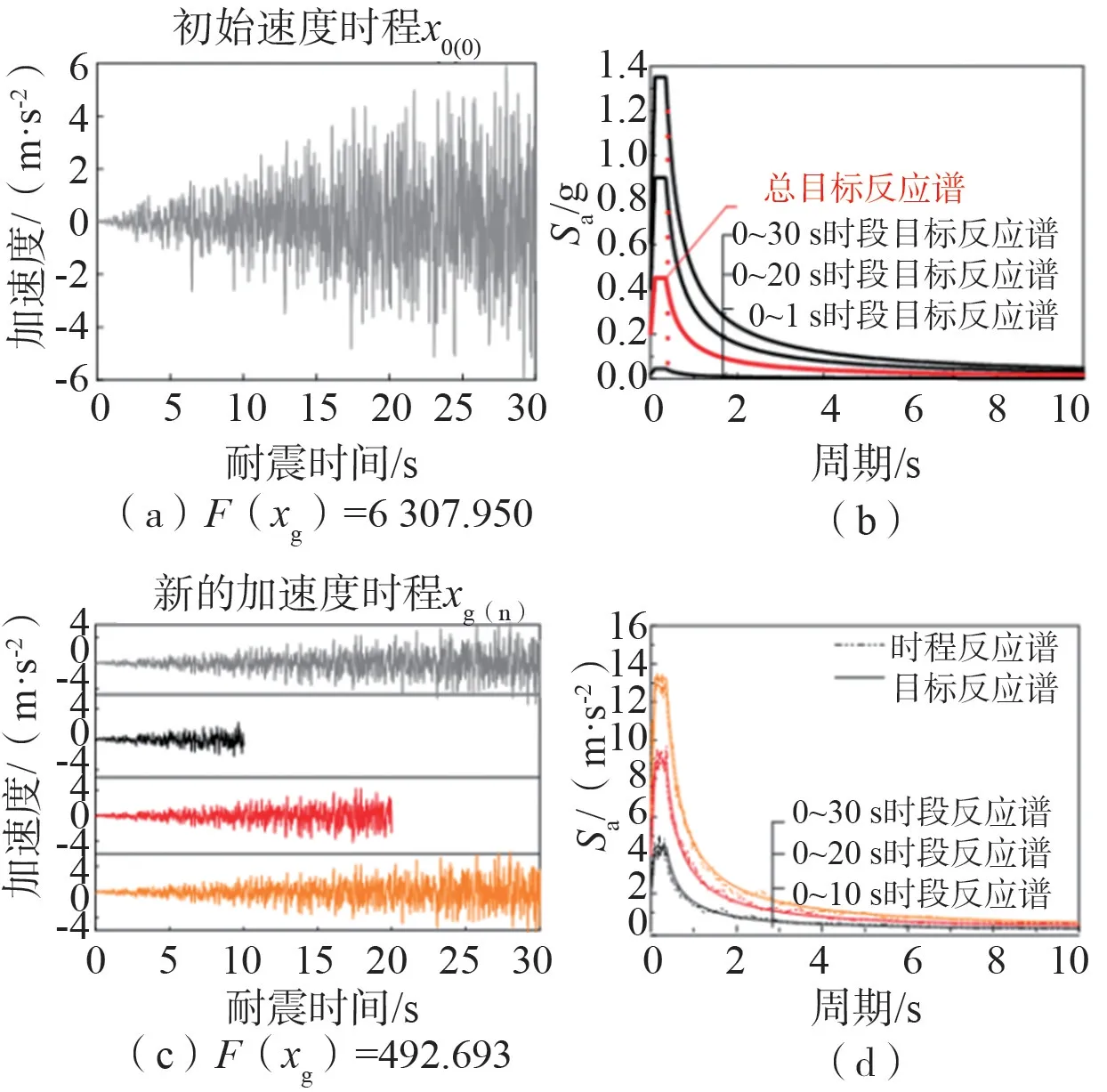
圖2 ETEFs曲線擬合的過程Fig.2 Fitting process of ETEFs curves

針對初始加速度時程，如圖2（b）所示，采用Newmark-β法計算不同時刻t下的分時段內時程反應譜Sa（T，t）。利用MATLAB優化工具箱中的lsqnonlin函數求解函數值F（x0（n））；并進一步優化調整得到新的加速度時程反應譜Sa（T，t）和加速度時程xg（n）。最后，重新計算調整后的目標函數值F（xg（n））。

當|F（x0（n））-F（xg（n））|＞［b］時（本算例中函數容許閥值［b］取為10-3），則重新進行迭代優化。否之，則迭代終止，得到符合要求的ETEFs曲線。圖2（c）-圖2（d）為經過n次迭代后的加速度時程及加速度時程的反應譜。

本文采用3條不同的初始加速度時程擬合得到3條ETEFs曲線。圖3（a）為擬合過程中目標函數值F（xg）變化曲線。可以看出：初始時F（xg）很大；經過10次迭代后，F（xg）變化逐漸變小；最終，當目標函數值F（xg）變化值的函數精度達到容許閥值［b］時迭代終止。當不同初始值加速度不同時，循環迭代次數也有所不同。圖3（b）為最終擬合得到的3條ETEFs曲線。可以看出：本文擬合ETEFs曲線加速度均隨著時間的增加而持續增大。

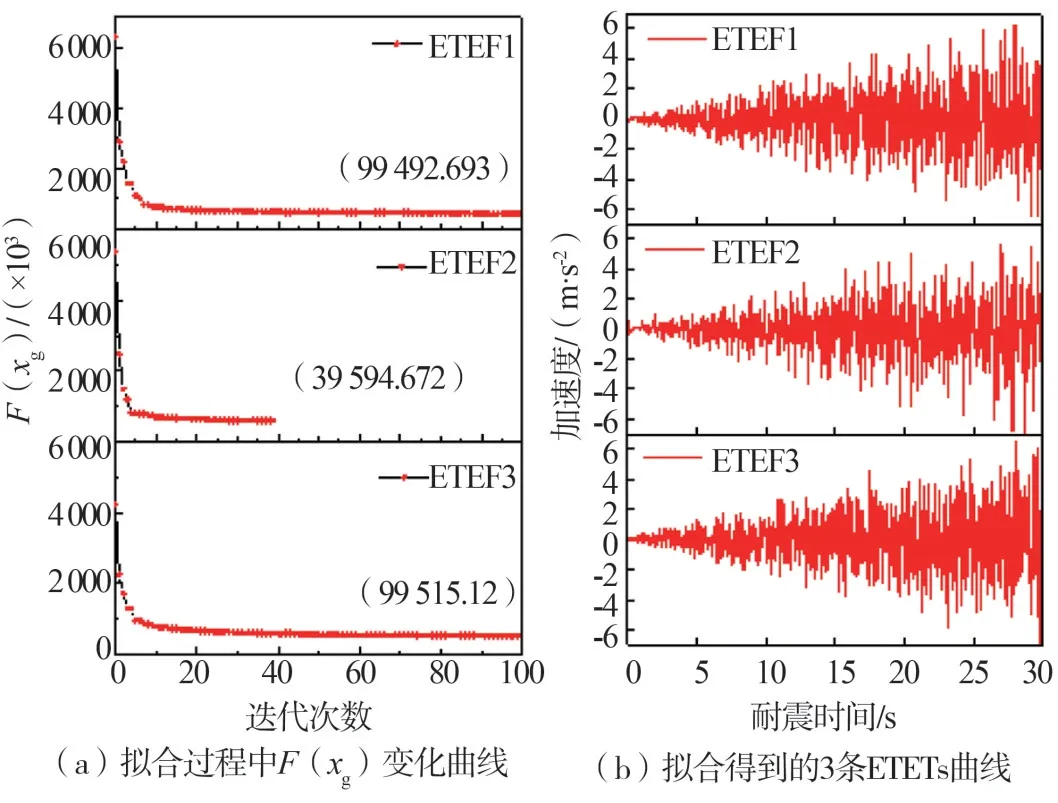
圖3 擬合得到的3條ETEFs曲線及目標函數值Fig.3 ETEFs curves and objective function value

2.2 SDOF體系及數值模型

本小節采用彈塑性SDOF體系為研究對象，其模型如圖4所示，在對結構進行動力分析時，通常將結構質量理想化為集中質量m，c為體系阻尼，k為剛度矩陣。

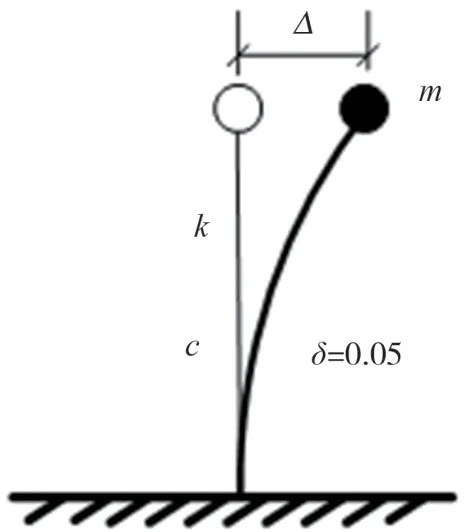
圖4 彈塑性SDOF模型Fig.4 Elastic-plastic model of SODF

在本文算例中：通過OpenSEES有限元軟件，建立非線性SDOF體系的數值模型。選擇Nonlinear Beam-Column非線性梁柱單元，用Steel01模型的雙折線來模擬單自由度非線性特性，如圖5所示。其中：屈服強度Fy為337 MPa，初始的彈性模量E0為203 GPa，剛度比b為0.1。

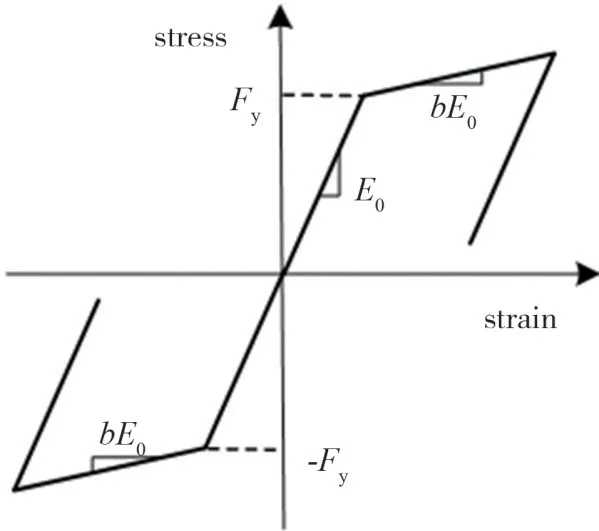
圖5 Steel01模型Fig.5 Steel01 model

該算例中質量m=160 kg，系統阻尼比δ取為0.05。基于以上參數，可以計算得到SDOF體系的基本自振周期T1為1.1 s。

2.3 SDOF體系地震響應分析

根據本文合成的3條ETEFs曲線作為地震動輸入，分別施加在彈塑性SDOF體系上，計算得到SDOF體系的位移響應。以ETEF1曲線作用下響應為例，位移時程及最大位移如圖6所示。可以看出：SDOF體系在ETEF1時程輸入下位移響應呈現往復變化，為了更好地表達位移響應隨時間增長的趨勢，將往復的位移響應，通過式（4），將轉化為位移絕對值的最大值的形式，后文均表述為：最大位移時程。

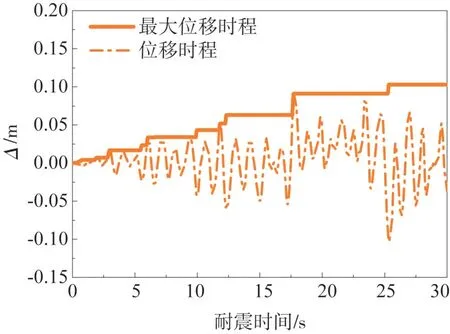
圖6 SDOF的累積位移時程曲線（ETEFs1）Fig.6 Cumulative displacement-time history curves of SDOF（ETEFs1）

圖7為SDOF體系采用ETA法得到的最大位移響應時程圖。可以看出：分別在ETEF1、ETEF2和ETEF3時程下的位移峰值結果都隨時間的增加而不斷增大，其耐震時程分析結果呈鋸齒向上的趨勢。為了比較3條時程下的耐震時程結果的離散性，列出了耐震時程法分析結果的中位值。對比發現：三者的分析結果與中位值較為接近。

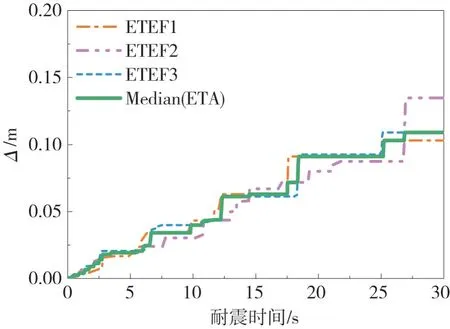
圖7 SDOF的位移時程曲線Fig.7 Displacement-time history curves of SDOF

對ETA分析結果中位值進行分段擬合得到的擬合曲線如圖8所示。考慮到框架結構在小地震作用下為彈性響應，隨著地震波的增大才逐漸進行彈塑性狀態。因此，以目標時間點tTarget為界限（對應于E1水準）進行分段擬合。當t≤tTarget時，認為結構處于彈性狀態，采用線性擬合，相關系數R2為0.984 45；當t＞tTarget，認為結構逐步進入彈塑性，采用三次多項式擬合，相關系數R2為0.941 48。

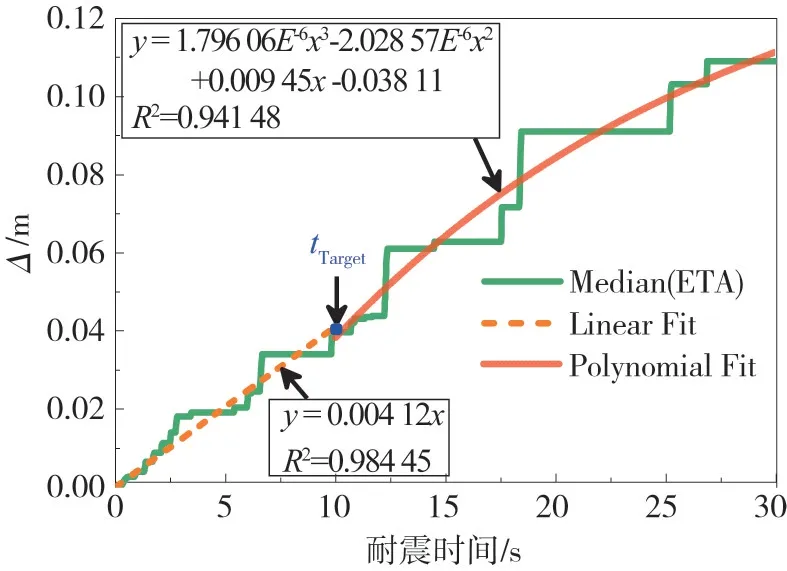
圖8 最大位移時程的擬合結果Fig.8 Fitting results of maximum displacement time history

3 鋼筋混凝土框架彈塑性地震響應分析

3.1 框架結構參數及數值模型

本文以文獻［6］中5層3跨的鋼筋混凝土框架結構作為算例結構。由于結構對稱，選取該結構中一榀平面框架作為研究對象，如圖9（a）所示。梁柱混凝土強度等級為C30，梁柱縱筋為HRB400，箍筋為HRB335。結構的平面、立面及恒荷載分布如圖9（b）所示。其它結構參數請詳見文獻［6］。基于OpenSees有限元軟件，建立鋼筋混凝土框架的有限元模型，如圖10所示。

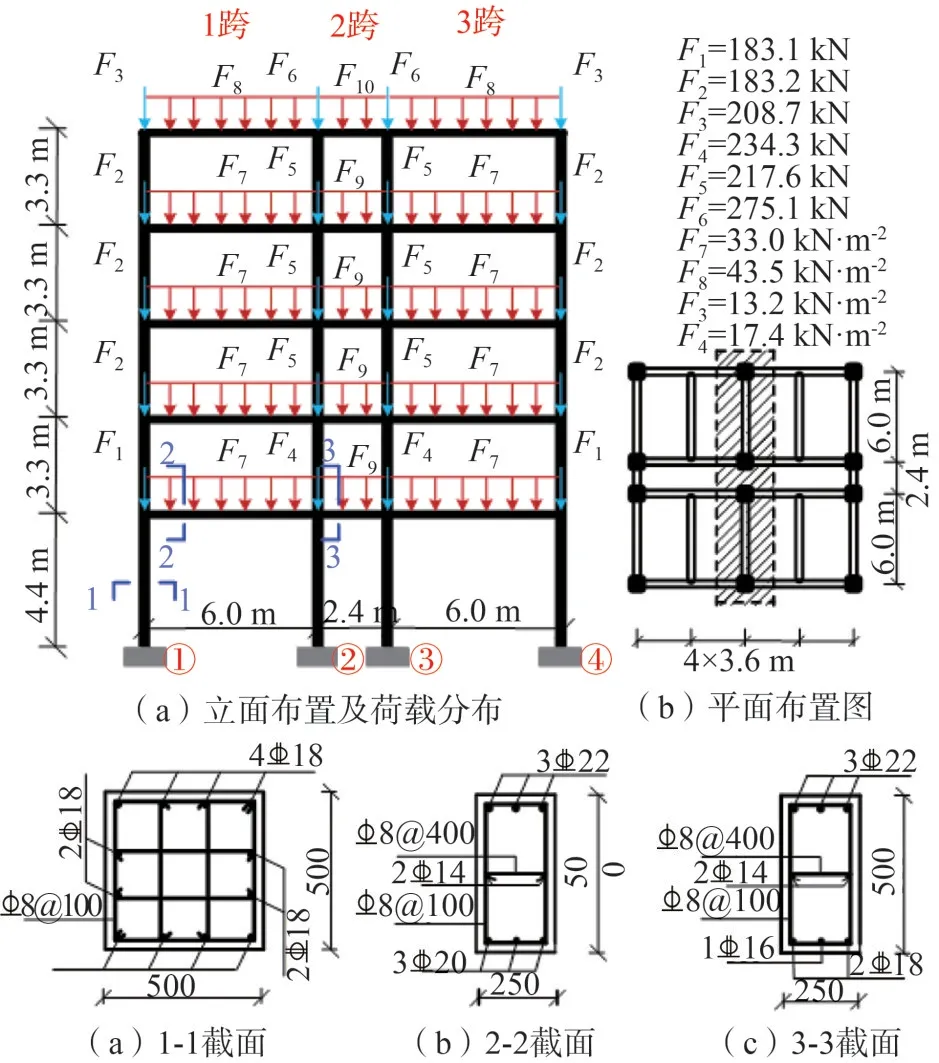
圖9 框架結構模型Fig.9 Structural frame model

構件采用分布塑性梁柱（Nonlinear Beam Column）纖維單元，鋼筋和混凝土的本構關系分別采用為Giuffre-Menegotto-Pinto模型（如圖10（f）所示）和經Scott修正的Kent-Park模型（如圖10（e）所示）。其中：鋼筋采用屈服強度400 MPa、彈性模量200 GPa和應變強化率0.02的Steel02材料。混凝土材料用Concrete01模型，其中：又可分為保護層混凝土和核心區約束混凝土，其模型數據見表1。采用經典Rayleigh阻尼，阻尼比取為0.05。

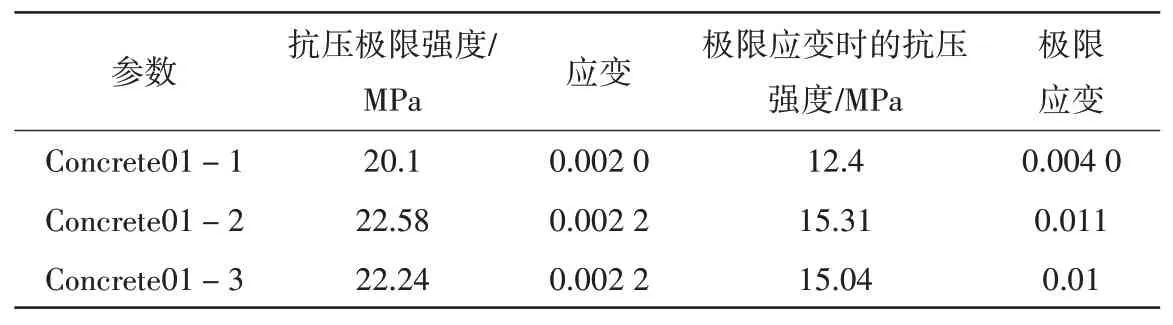
表1 Concrete01模型數據Table 1 Parameters of Concrete01

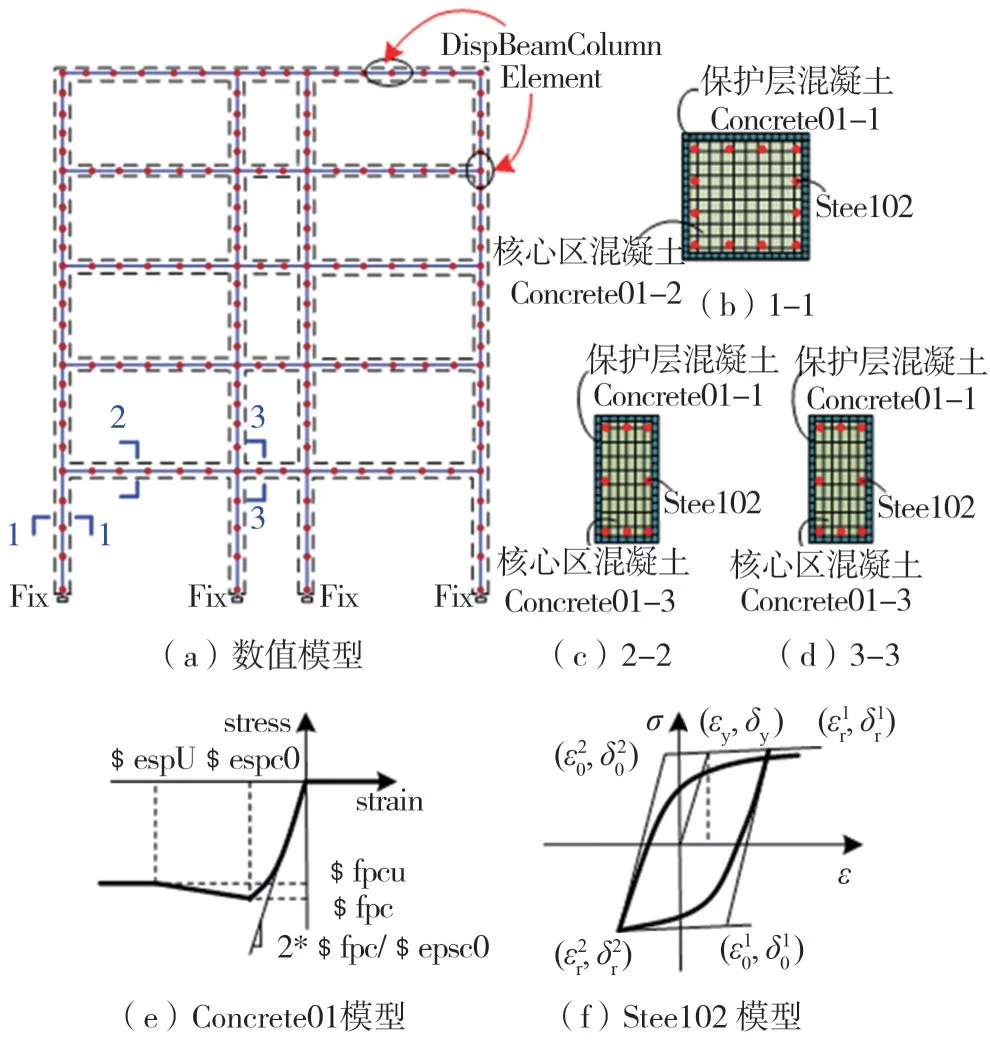
圖10 框架結構有限元模型Fig.10 Finite element model of frame structure

算例框架結構的設計烈度為8度，場地類別為II類，根據2.1節合成的3條ETEFs曲線作為地震動輸入，采用ETA法分析探究該框架的地震響應。為了對比驗證，同時采用3.2節中的18條天然地震動作為地震動輸入進行IDA分析。

3.2 IDA分析方法的結果驗證

IDA的計算結果通常表達為地震動強度指標（intensity measure，IM）和結構的工程需求參數（engineering demand parameters，EDP）之間的關系。由于反應譜曲線上的每一點都需要進行一次時程分析，每一條地震動記錄對應1條IDA曲線，變換地震動，可獲得多條IM-EDP曲線。目前，通常選用峰值加速度PGA或對應于結構第一周期的譜加速度Sa（T1），作為IM指標［7］。

然而，耐震時程分析結果表征為tE-EDP的關系。為了使ETA方法與IDA方法的結果具有可比性，需將IDA的地震動強度指標IM與耐震時間tE進行轉換。

根據美國（ATC-63）［8］報告，本文采用Sa（T1）作為IM指標。基于等步長調幅方式，可將不同調幅的地震動幅值與時間根據式（5）進行換算。

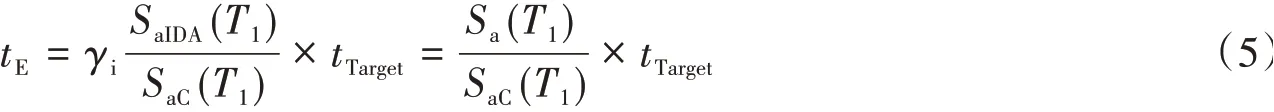
式中：SaIDA（T1）和Sa（T1）分別為IDA法中單條地震波調幅前后的譜加速度值；γi為IDA法中單條地震波第i次的調整系數；tE為單條地震動不同強度的等效耐震時間。

本文從PEER得到了18條地震動記錄見表2。選波標準為：震級范圍確定為6～8級，剪切波速v30的范圍為360～760 m/s，目標反應譜為本文2.1節中的總目標反應譜，地震波在［0.1 s，10 s］內須與總目標反應譜較吻合。

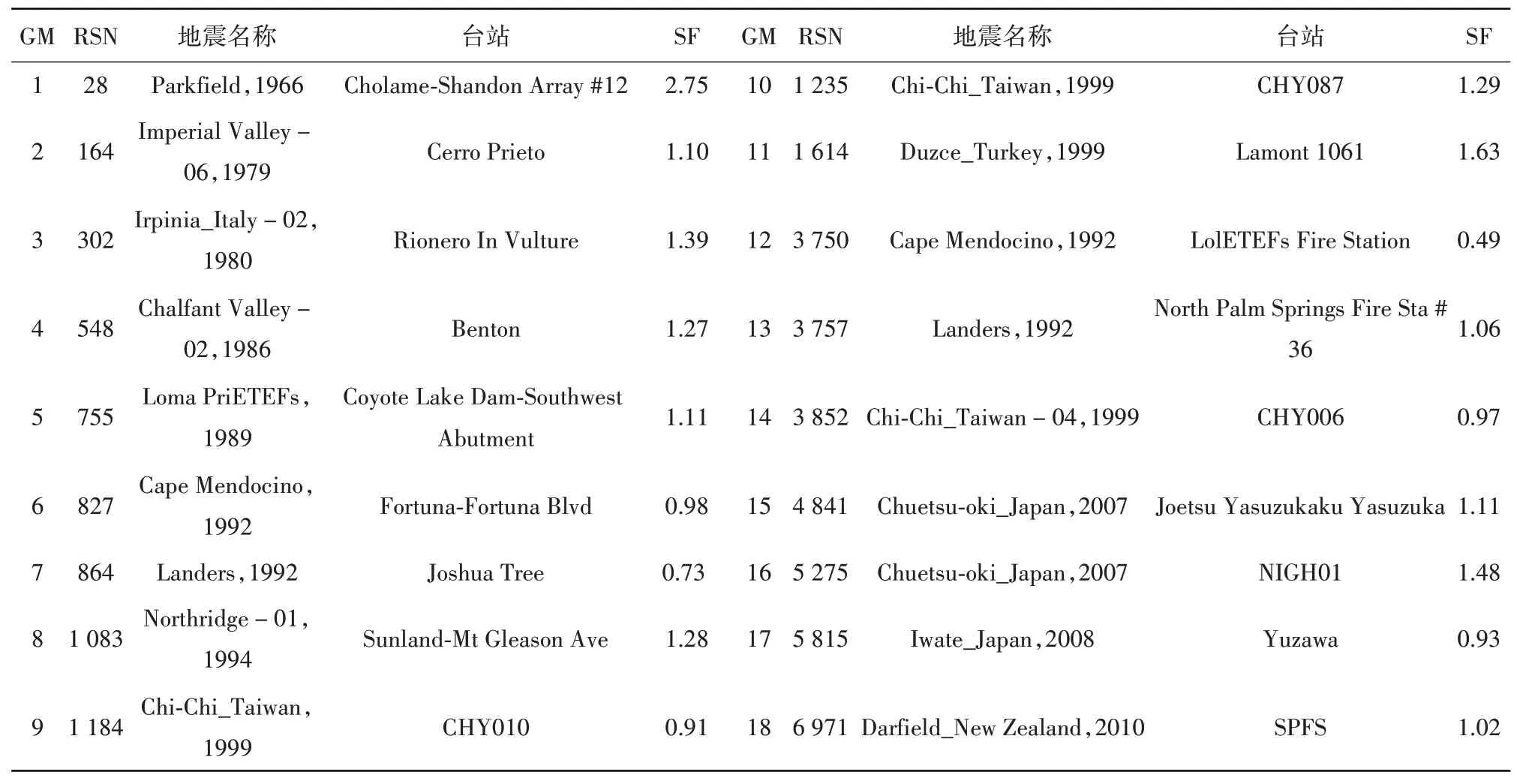
表2 PEER數據庫篩選得到的18條地震動記錄Table 2 18 Ground motion records from PEER

3.3 頂點位移響應分析及對比

頂點位移是結構抗震性能中重要的指標之一，通常與基底剪力一起來表征結構剛度與延性的變化。圖11（b）給出了ETA法和IDA法分析的頂點位移結果相關性分析圖。橫縱坐標分別為相同時間點下，ETA的擬合值與IDA中位值。對這些離散點進行線性擬合，得到該曲線的線性系數為0.999 48，說明整體上IDA中位值與ETA的擬合值約為0.999 48倍關系。擬合相關系數R2為0.998 67，R2∈［0，1］，其值越接近1，說明兩者相關性越好，離散性越小。

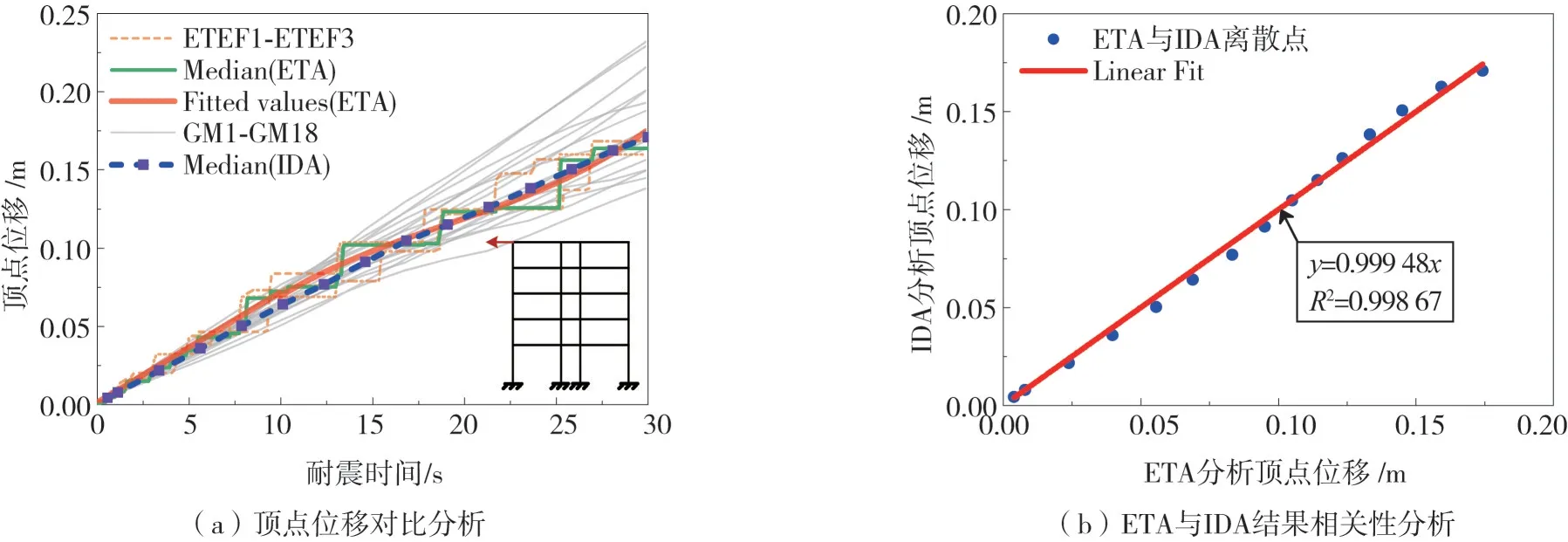
圖11 頂點位移對比分析及結果相關性分析Fig.11 Top displacement analysis and results correlation analysis

3.4 基底剪力分析及對比

基底剪力是結構抗震性能中重要的指標之一，其值表明了結構抗震側向力的大小。圖12（b）給出了ETA法和IDA法分析結果的相關性分析圖。橫縱坐標分別為相同時間點下，ETA擬合值與IDA中位值。對這些離散點進行線性擬合，得出兩者的線性關系為0.959 83倍，擬合相關系數R2為0.999 79，接近1，相關性好。

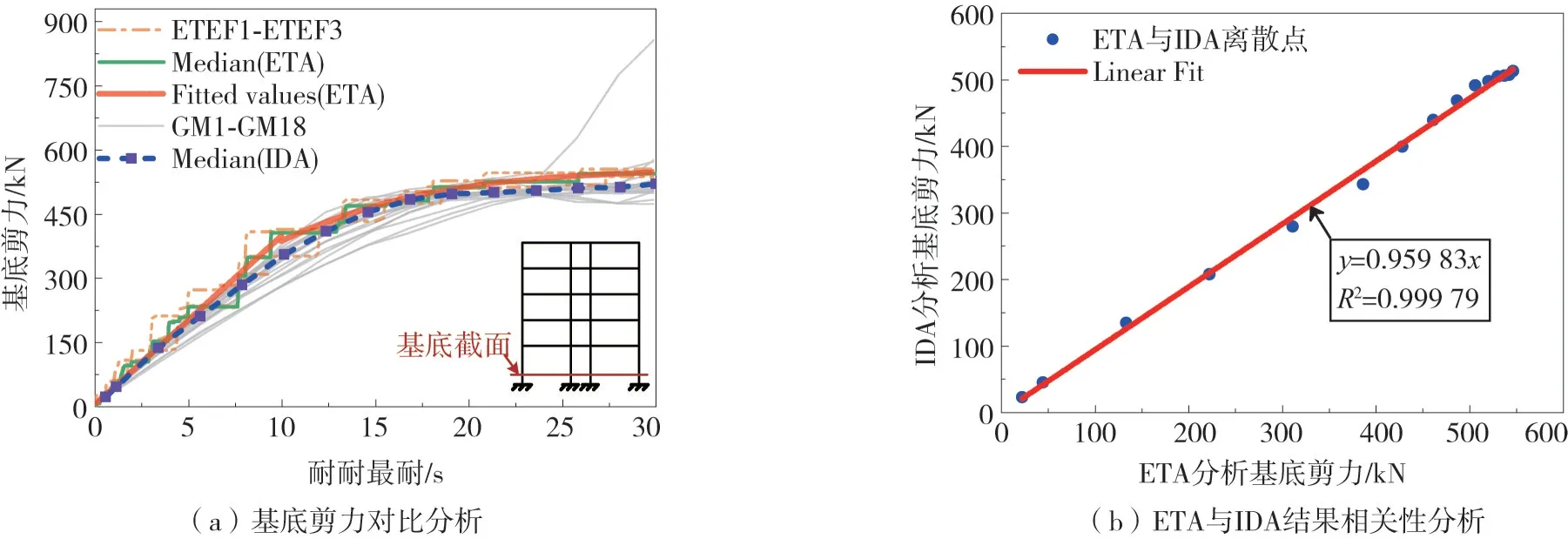
圖12 基底剪力對比分析及結果相關性分析Fig.12 Base shear analysis results correlation analysis

4 鋼筋混凝土框架的地震損傷發展

為了探究ETA法能否預測結構在大震下的損傷發展模式，本節使用ETA法分析強地震作用下結構構件損傷失效的發展情況。本文以構件的塑性鉸分布及出現概率來表征結構損傷情況。根據結構設計烈度為8度，確定結構的最大地震影響系數Smax為1.147 5 g，因此其對應的耐震時間tE為25.5 s，即僅采用前25.5 s。同時，為了對比驗證，同時采用3.2節中的18條天然地震動作為地震動輸入進行IDA分析。

4.1 塑性鉸出現的概率分析

圖13為框架結構分別在3條ETEFs曲線輸入下，結構梁柱塑性鉸出現的情況。從圖中可以看出：對于柱構件，在結構柱底都出現了塑性鉸，其余部位都未出現塑性鉸的情況；3條ETEFs時程下的結果均一致。對于梁構件，1～4層梁端幾乎都出現了塑性鉸；但3條ETEFs時程下的結果有所不同。總體來說：耐震時程結果相差不大。

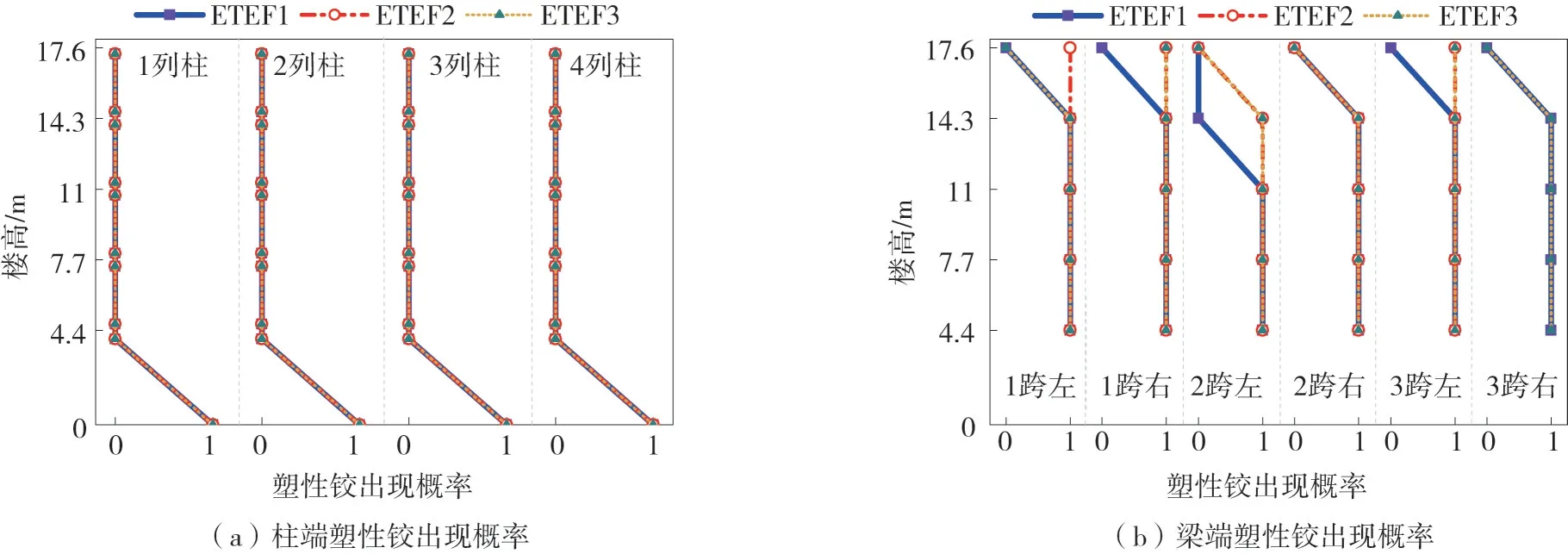
圖13 3條ETEFs時程下梁柱塑性鉸出現概率分布圖Fig.13 Probability distribution of plastic hinge in time history analysis

對框架結構采用ETA法與IDA法時的分析結果進行對比，圖14為大震作用下兩種方法分析時的塑性鉸出現次數概率統計。可以看出：底層柱底均大概率的出現塑性鉸，1～4層梁端也幾乎全都出現塑性鉸，對于邊柱和梁的塑性鉸出現的概率擬合大致吻合。然而，對于中柱，兩種方法得到的塑性鉸出現概率有一些偏差。這是由于3條ETEFs曲線下的耐震時程結果中，塑性鉸出現概率只有0、1/3、2/3和1四種情況。而18條天然地震動下的IDA分析結果能出現比較相近且連續的塑性鉸概率值。因此，ETA分析會低估結構的出現損傷的情況。可以預期的是：若多采用多條ETEFs曲線作為輸入時，結構構件塑性鉸出現概率的評估結果將會大大改善。

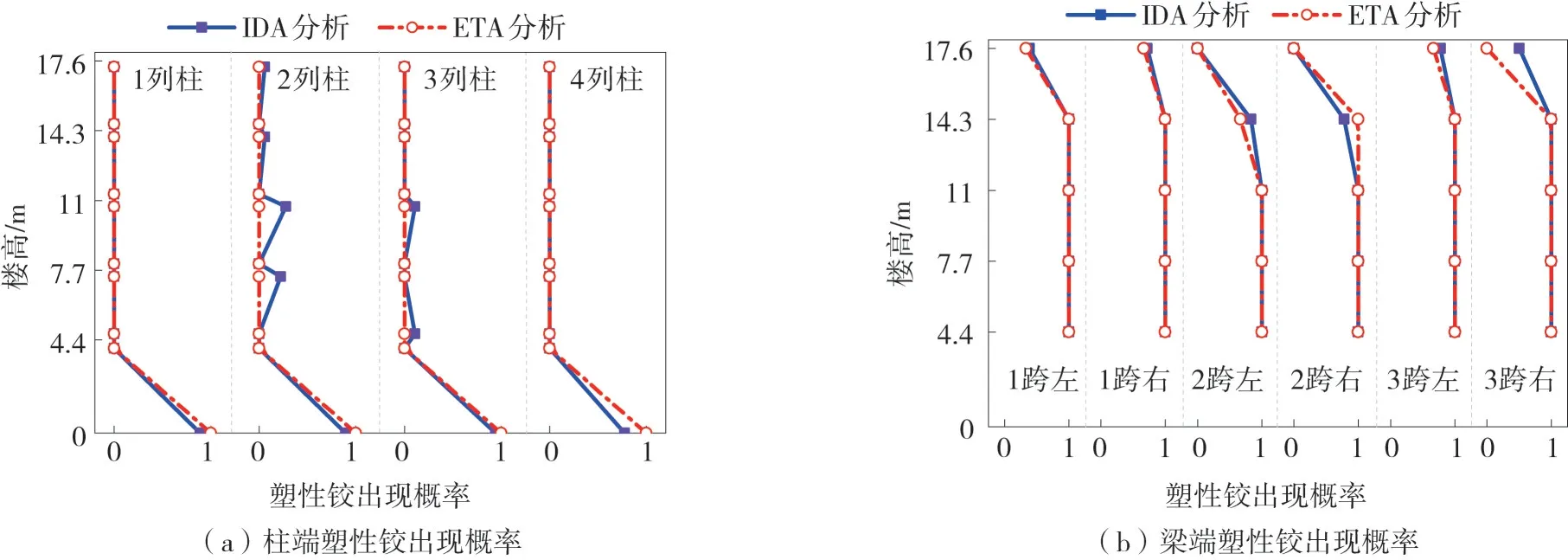
圖14 大震作用下塑性鉸出現概率Fig.14 Occurrence probability of plastic hinge under strong earthquake

4.2 塑性鉸出現順序對比分析

本節對結構構件塑性鉸的出現順序進行分析。采用統計的方法進行描述，即對于結構構件部位，計算其在每條地震動輸入下塑性鉸出現順序，再將n條地震動激勵下結構構件塑性鉸的出現順序值求平均值，最后將結構的每一個部位的平均值進行排序［9］。圖15（a）為本文3條ETEFs曲線作為時程輸入時，塑性鉸出現順序分布圖。可以看出：在耐震時程輸入下，塑性鉸首先出現在1層的梁端，從底層梁端依次向高層梁端發展塑性鉸，其次發生在底層柱底，最后出現在頂層梁端。

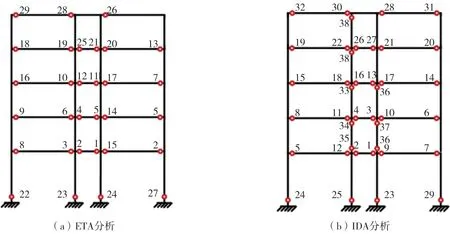
圖15 大震作用下塑性鉸出現順序Fig.15 Occurrence order of plastic hinge under strong earthquake

同理，圖15（b）為輸入18條地震動的情況下采用IDA方法時的梁柱塑性鉸出現順序分布圖。與ETA法的結果進行對比，可以發現：兩種時程輸入下的分析結果，塑性鉸出現順序趨勢一致。對于IDA的分析結果，最終還有一些塑性鉸出現在柱端；而對于ETA分析結果，則沒有出現柱端塑性鉸。比較兩種方法所得到的塑性鉸出現順序分布圖可以得知：ETA方法會略低估結構的出現損傷的情況，但大致上能有效預測結構最可能發生的塑性鉸的位置和塑性鉸的發展趨勢。

4.3 梁柱最大轉角分布及對比

圖16為框架結構在大震下，分別用ETA方法和IDA方法分別進行分析時，得到的構件桿端的最大轉角結果。從圖中可以看出：在兩種方法下結構桿端的轉角結果吻合較好，其中底層柱腳與1～3層的梁端轉角較大，頂層的梁端轉角較小。可以表明：ETA方法能夠有效地預測結構構件的損傷大小。

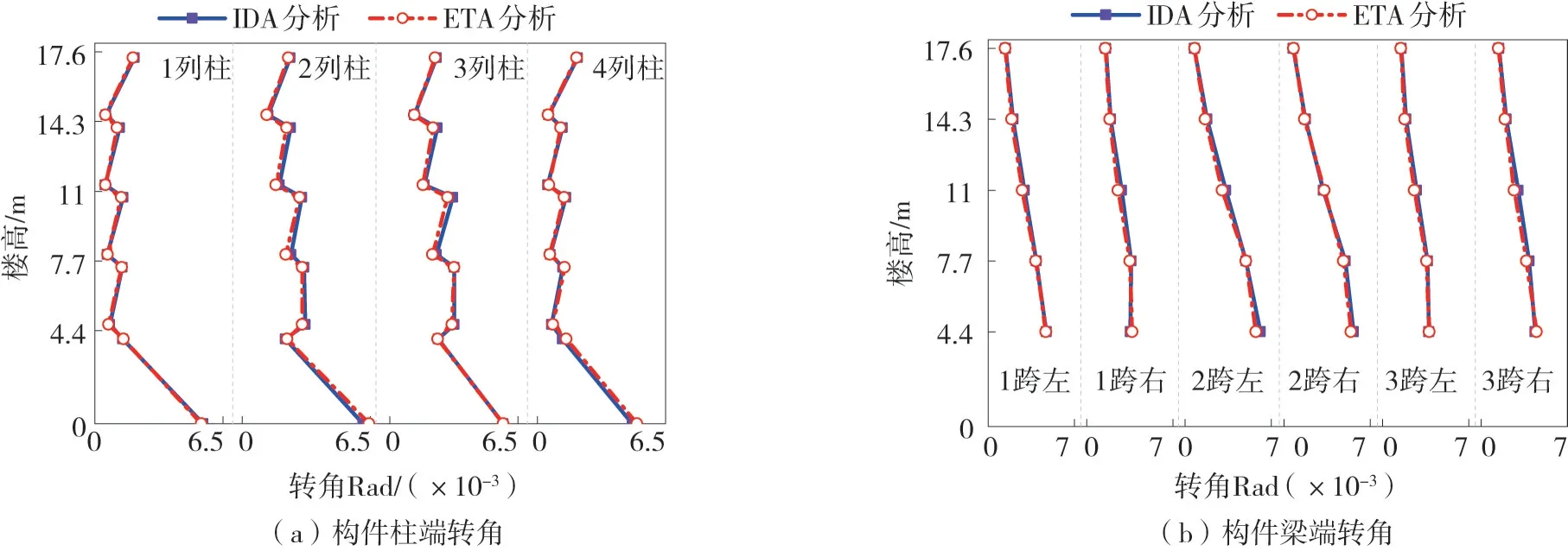
圖16 大震作用下構件桿端轉角Fig.16 Components’angle in rod end under strong earthquake

5 結論

本文對耐震時程曲線的擬合思路進行了分析，合成了3條耐震時程曲線，并以彈塑性SDOF體系為例，評估了耐震時程曲線擬合的可行性，再以鋼筋混凝土框架結構為例，探究了ETA法用于評估混凝土框架結構響應及失效模式的適用性。主要得出的結論如下：

（1）以選定的規范譜為目標反應譜，擬合得到的耐震加速度時程曲線具有峰值加速度隨時間增加而增大的特性；且耐震時程反應譜在任一時間段內都能很好的與目標反應譜吻合。

（2）采用ETA法和IDA法對混凝土框架結構的地震響應進行分析，并對兩者的結果進行了對比分析，分析結果表明：兩種方法對頂點位移和層間位移角的響應較一致；而最大基底剪力的ETA分析結果略大。

（3）大震下的鋼筋混凝土框架結構的倒塌分析結果表明：ETA方法較為準確地預測了結構的塑性鉸分布及塑性鉸發展順序。當采用多條耐震時程加速度曲線作為輸入時，評估結果準確性更高。

綜上所述，由于ETA方法僅需進行少量幾條耐震時程分析，計算十分高效，因此ETA方法可以成為預測結構的失效模式的高效方法。