基于ANSYS Workbench的錨鏈輪輕量化設計

王 杰，王 震，陳 超，駱書虎，邵振華

（1.江蘇科技大學機械工程學院，江蘇 鎮江 212003；2.江蘇政田重工股份有限公司，江蘇 南通 226000）

0 引 言

當前船舶工業正朝著“綠色船舶”的方向發展，錨絞機作為船舶錨泊系統的重要配套設備，其在技術上也正朝著經濟、節能、綠色環保的方向發展［1］。錨鏈輪作為錨絞機在起錨、拋錨、系泊和帶纜時與錨鏈直接接觸的部件，其結構設計的可靠性對保障錨機和船舶的安全運行有重要影響［2］。傳統的錨鏈輪主要根據GB／T 3179—1996標準設計，往往依靠經驗公式，采用較高的安全系數保證結構的安全性，缺少比較精確的強度計算，這使得錨鏈輪的體積龐大，結構笨重，機械傳動效率不高，材料和能源浪費較多［3］。因此，對錨鏈輪輕量化技術進行研究，優化錨鏈輪結構，提高其傳動效率，是錨絞機和其他甲板機械未來發展的必然趨勢。

近年來，國內外已有很多學者對船用錨絞機各部件的輕量化設計進行研究，例如：李曦［4］對液壓錨絞機墻架進行了有限元分析，確定了墻架的優化設計空間，運用Optistruct軟件對墻架板厚進行了優化設計；李文釗［5］對錨絞機卷筒和制動機構進行了有限元計算，確認了結構的變形失效部位與實船故障部位的一致性，利用NX NASTRAN軟件對失效部位進行了優化設計；WU等［6］對錨機底座進行了靜力學分析和模態分析，得到了底座模型可優化的空間，利用ANSYS軟件對底座結構進行了拓撲優化設計；王志明［7］對船用錨機的鏈輪軸進行了剛柔耦合仿真分析，得到了鏈輪軸在實際工況下的動應力歷程，為鏈輪軸的優化設計提供了理論依據。本文以船用錨機的錨鏈輪為研究對象，利用ANSYS Workbench軟件對其進行瞬態動力學分析和預應力模態分析，并基于多目標遺傳算法（Multi-Objective Genetic Algorithm，MOGA）對錨鏈輪的尺寸進行優化，探尋對錨鏈輪進行輕量化設計的可行性和最終能達到的輕量化程度。

1 錨鏈輪有限元分析

本文以正多邊形嚙合的五齒錨鏈輪為研究對象，采用SolidWorks軟件對其進行三維建模。為建立準確的三維實體模型，在創建錨鏈輪模型時要充分考慮其可能遇到的工況和安裝要求。同時，為提高后期有限元網格劃分的質量，提升有限元分析的精度和計算速度，根據圣維南原理［8］，對模型進行適當的簡化，去掉對有限元計算影響不大的螺栓孔和倒角。錨鏈輪簡化模型見圖1。

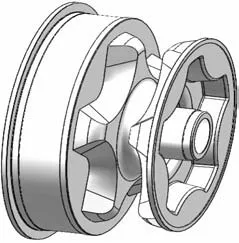
圖1 錨鏈輪簡化模型

1.1 瞬態動力學分析

首先，為保證模型在導入軟件過程中的完整性，避免元素丟失，將錨鏈輪三維實體模型以x_t格式導入ANSYS Workbench中；其次，定義錨鏈輪的材料屬性，本文參照日本標準SC450（相當于國標ZG 230-450）選取錨鏈輪材料，其屈服強度為230 MPa，彈性模量為2.11×105MPa，泊松比為0.311，密度為7.83 g／cm3；最后，對錨鏈輪進行有限元網格劃分，綜合考慮計算量和計算精度，設置單元格大小為40 mm，采用自由網格劃分的方式，劃分的網格單元數為79 374個，節點數為137 654個。創建的錨鏈輪有限元網格模型見圖2。

圖2 錨鏈輪有限元網格模型

在錨機進行起錨操作過程中，錨鏈輪與錨鏈只有1～2個齒相嚙合，這里為簡化分析，只考慮1個齒與錨鏈相嚙合的情況，錨鏈輪的受力區域為圖3中的區域A。由于錨鏈輪的受力面為曲面，很難確定其受力方向，這里以曲面上所受壓力代替錨鏈與錨鏈輪嚙合時產生的嚙合力。已知錨鏈輪過載時所受拉力F為858 kN，曲面面積A為0.029 4 m2，則曲面所受拉力P為

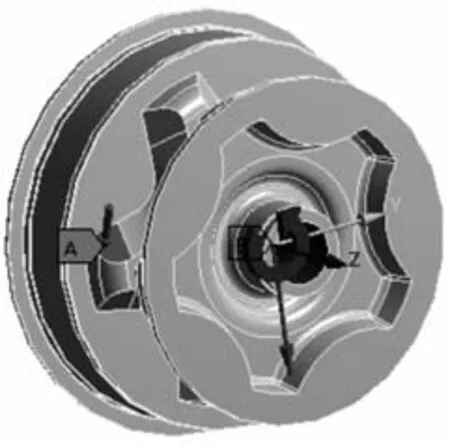
圖3 錨鏈輪載荷添加

瞬態動力學分析以錨鏈輪過載時刻為中心，分析過載瞬間前后共計0.1 s時間內錨鏈輪所受應力的變化情況。首先，設置錨鏈輪瞬態分析初始時間載荷步為0.002 s，最短時間載荷步和最長時間載荷步分別為0.002 s和0.010 s，計算周期為0.100 s；其次，在錨鏈輪上添加一個轉動副，并給定一個轉速，使錨鏈輪的轉速在前半個周期內迅速增加到1 rad／s，在后半個周期內保持不變；最后，將大小為29.18 MPa的壓力載荷添加到嚙合曲面上，方向為垂直于曲面（見圖3），并確保載荷在0.050 s內迅速增大到最大值，在結束時刻減小到0。設置完成之后，開始進行分析計算，得到錨鏈輪在1個周期內的應力變化曲線，見圖4。

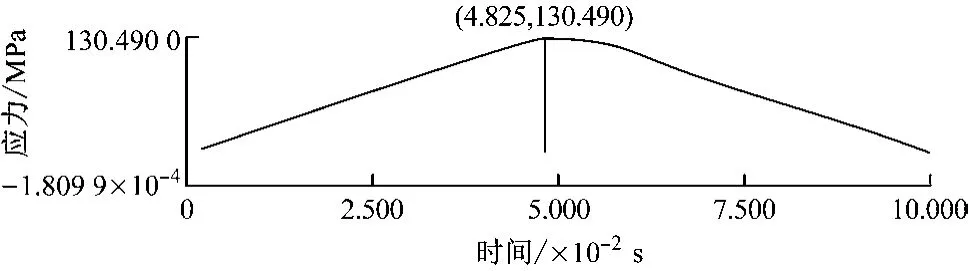
圖4 0～0.100 s內錨鏈輪應力變化曲線

由圖4可知，隨著錨鏈輪所受壓力的不斷增大，其最大等效應力值也不斷增大，并在0.048 25 s時達到最大，此時錨鏈輪等效應力云圖和總變形位移云圖分別見圖5和圖6。由圖5和圖6可知，錨鏈輪最大應力出現在鏈輪軸與錨鏈輪內壁連接處，最大等效應力值為130.49 MPa，遠小于錨鏈輪材料的屈服強度，此時其側壁的最大位移變形量為15.127 mm，滿足輕量化設計需求。

圖5 0.048 25 s時錨鏈輪等效應力云圖

圖6 0.048 25 s時錨鏈輪總變形位移云圖

1.2 預應力模態分析

錨鏈輪在起錨過程中一直處于轉動狀態，不僅要滿足強度要求，而且要滿足振型和固有頻率要求，避免與其他部件產生共振，因此要對其進行模態分析。

首先，將錨鏈輪實體模型以x_t格式導入ANSYS Workbench軟件中；其次，在Workbench模態分析系統中定義錨鏈輪的材料屬性、單元格大小和網格劃分方式；接著，在錨鏈與錨鏈輪嚙合處添加一個垂直于受力面的壓力，同時在鏈輪內孔面添加圓柱約束，以約束錨鏈輪的徑向運動和軸向運動，只讓其有圓周方向的轉動；最后，取模態階數為6進行模態分析計算。錨鏈輪模型固有頻率值和振型云圖分別見表1和圖7。

圖7 錨鏈輪前6階模態振型云圖

表1 錨鏈輪固有頻率值

從表1和圖7中可看出：錨鏈輪的前3階模態的固有頻率值在173.65～183.61 Hz，是錨鏈輪的主要振動模態；錨鏈輪的后3階模態的固有頻率值都在186.30 Hz以上，是錨鏈輪的局部振動模態。錨鏈輪工作時，鏈輪軸轉動和齒輪傳動產生的激振頻率都在100 Hz以下，遠低于錨鏈輪的最低固有頻率，因此錨鏈輪不會與其他部件產生共振，其動態特性滿足設計要求。

2 錨鏈輪尺寸優化設計

由錨鏈輪的瞬態動力學分析和預應力模態分析結果可知，錨鏈輪的原結構模型仍具有一定的優化設計空間，而錨機工作時錨鏈與錨鏈輪的嚙合面為曲面，且錨鏈輪齒形設計相對標準化，因此對錨鏈輪的齒形進行優化較為困難。這里在上述有限元分析的基礎上，只針對錨鏈輪的輪轂和側壁等應力較小的部位進行尺寸優化。

1）錨鏈輪的實體模型是由截面旋轉拉伸得到的，優化錨鏈輪結構就是對截面尺寸進行調整。錨鏈輪旋轉拉伸截面圖見圖8。

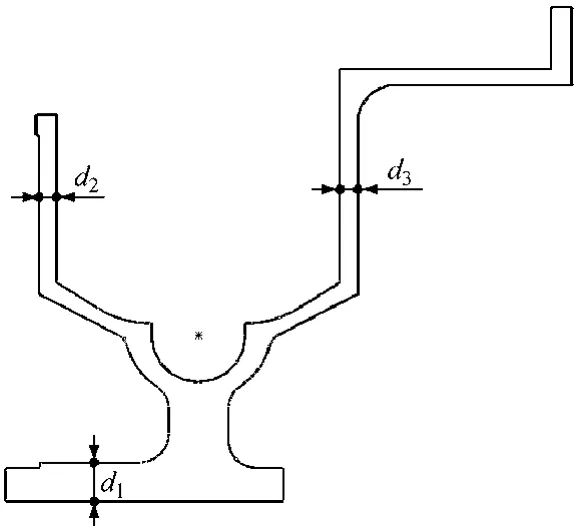
圖8 錨鏈輪旋轉拉伸截面圖

這里以錨鏈輪輪轂的厚度d1、兩側壁的厚度d2和d3為設計變量，以錨鏈輪的最大應力為約束條件，以最小化質量和一階固有頻率為優化目標，要求錨鏈輪的質量M在允許的范圍內盡可能地小，其1階固有頻率fn1在允許的范圍內盡可能地高，構建2個目標函數，即：F1（X）＝min M（X）；F2（X）＝max fn1。

錨鏈輪尺寸優化數學模型為

式（2）中：d1為輪轂的厚度；d2為左側壁的厚度；d3為右側壁的厚度；F1（X）為最小化質量；F2（X）為最大應力。

2）根據建立的錨鏈輪尺寸優化模型，運用ANSYS Workbench軟件的Design Explorer優化設計模塊對錨鏈輪進行基于MOGA的尺寸優化，整個優化過程見圖9。

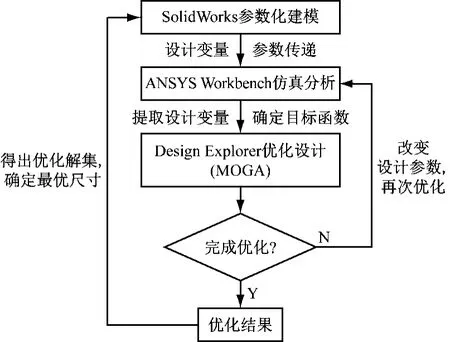
圖9 錨鏈輪結構參數優化流程

3）優化算例分析。

本算例利用ANSYS Workbench軟件提供的MOGA進行計算分析。該算法是非支配排序遺傳算法Ⅱ的變種算法，多用于對全局最小值和最大值進行求解［9-10］。優化算法具體參數設置：種群總數為100個；交叉概率和變異率分別為0.8和0.1；最大迭代次數為40次；最大候選點個數為3個。同時，使錨鏈輪質量函數最小化和一階頻率函數最大化，并約束最大應力，使其小于許用應力值。優化迭代過程以Pareto解集前沿分布80%的樣本收斂，最終經過40次迭代之后得到1組Pareto最優解集，并生成3組最合理的優化設計結果。得到錨鏈輪初始結構和3種優化方案對比見表2。

表2 錨鏈輪初始結構和3種優化方案對比

4）優化結果。

從表2中可看出，3組優化方案的設計變量都在一定的區間內趨于穩定，為得到最優的優化結果，分別針對3組數據重新建模，并對得到的錨鏈輪模型進行瞬態分析，結果見圖10。由圖10可知，在0.1 s時間內，優化方案三的錨鏈輪的彈性變形量最小，最大彈性變形量為4.973 4×10－4mm，因此確定優化方案三為錨鏈輪的最佳優化方案。

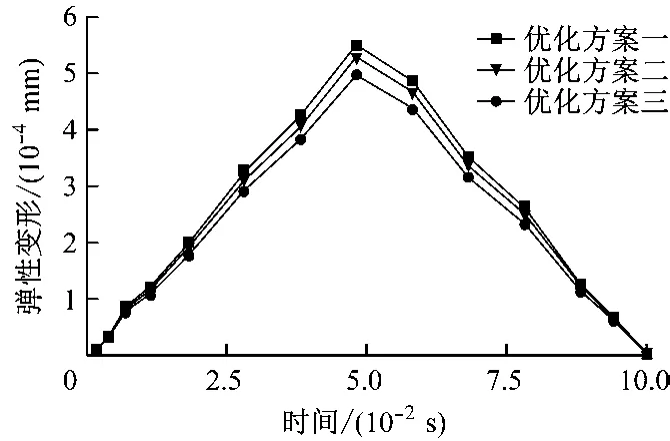
圖10 錨鏈輪3組優化方案彈性變形量對比

3 優化錨鏈輪驗證分析

考慮后續機械加工的需求，對優化方案三的各尺寸作圓整化處理，即d1＝10 mm，d2＝36 mm，d3＝31 mm，得到最終的優化結構。添加與優化前相同的邊界條件和載荷狀況，分析驗證優化后錨鏈輪的動態特性，結果見圖11和圖12。由圖11和圖12可知：優化后錨鏈輪的最大應力值由原來的130.49 MPa增加到了134.72 MPa，仍在材料的許用應力范圍內；優化后錨鏈輪的最大位移變形量由原來的15.127 mm增加到了16.603 mm，對錨鏈輪剛度的影響較小。表3為優化后基座模型固有頻率值。由表3可知，優化后錨鏈輪各階固有頻率均有所提高，其中1階固有頻率由原來的173.65 Hz增加到了184.45 Hz，較好地實現了1階固有頻率最大化的目標。

圖11 優化后錨鏈輪等效應力云圖

圖12 優化后錨鏈輪最大位移變形云圖

表3 錨鏈輪優化后基座模型固有頻率值

表4為錨鏈輪優化前后各性能參數對比。由表4可知：優化后錨鏈輪的總質量減少了118.73 kg，減重率為3.25%；優化后錨鏈輪的最大等效應力和總位移變形量略有增大，對錨機整體結構的可靠性不會產生影響；優化后錨鏈輪的固有頻率有所提高，遠大于鏈輪軸自身轉動和大小齒輪間傳動產生的激振頻率，對整體結構的穩定性不會產生影響。由此可知，基于MOGA對錨鏈輪進行輕量化設計能達到預期的效果，使錨鏈輪在滿足整體結構強度和剛度要求的同時，達到減輕重量的目的，滿足輕量化設計要求。

表4 錨鏈輪優化前后各性能參數對比

4 結 語

本文以正多邊形嚙合的五齒錨鏈輪為研究對象，通過對其輕量化設計的流程和方法進行研究，提出基于ANSYS Workbench軟件對錨鏈輪的結構進行優化設計。根據錨鏈輪的瞬態動力學分析和預應力模態分析結果，確定錨鏈輪的可優化區域，為其輕量化設計提供科學的理論依據；基于錨鏈輪力學分析結果，確定利用輪轂的厚度d1、兩側壁厚度d2和d3等3個參數構建以錨鏈輪質量最小化和1階固有頻率最大化為目標的尺寸優化數學模型；利用MOGA對錨鏈輪的尺寸進行優化，確定這3個參數的最優解集，并通過瞬態分析確定錨鏈輪尺寸的最終結構。通過對優化前后錨鏈輪的結構進行對比分析得出：優化后錨鏈輪的總質量減小了3.25%，較好地實現了減重的目的；同時，錨鏈輪的強度、動態特性和抗振性能得到了提高，滿足錨鏈輪設計的經濟性和安全性要求，為其他船舶的機械輔助設備的輕量化設計提供了理論依據。