常微分方程中的變換方法探究

楊繼昌，陳廣生，沈柳平，莫明忠，馬岱君，周昌永

（廣西科技師范學院數計學院，廣西 來賓 546199）

0 引言

常微分方程是一個理論研究和實際應用并重的學科，它在數學專業中具有很重要的地位，在體現客觀自然規律和解決實際問題方面也不可或缺[1]。

在高校數學類或理工類專業的《常微分方程》教材中列舉了很多種形式的常微分方程，其中最基本的一種就是變量分離方程，只需要用初等積分法即可求解。但是其他類型的常微分方程，我們最常用的方法就是變換方法。本文將對變換方法進行討論和研究，闡明它在求解常微分方程中的重要性。

1 一階常微分方程的變換方法及解題步驟和

1.1 變量分離法[2]

變量分離，其實質就是將未知函數或因變量與自變量分離出來，使等式的一邊為未知函數的導數，另一邊為自變量的導數形式.然后通過微分的逆運算，即兩邊同時積分，再逐步求出未知函數。

解：根據變量分離理論，此常微分方程可以變量分離為以下形式：

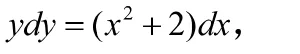
變量分離方程的基本形式為：

1.2 變量代換法

變量代換法的主要思想是對于一些微分方程形式上不是變量分離方程，若通過適當的變量代換后可以化為變量分離方程，再通過變量分離方程的求解方法求出變量代換后的方程的解，最后再將變量代換的解代回原來的變量就可以得到原方程的解。

1.2.1 齊次微分方程[3]

1.2.2 非齊次微分方程

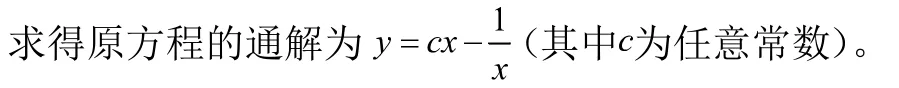
以上是對于形如（9）、（12）、（14）、（15）、（16）的微分方程求解問題中的變量代換法的應用，當然，還有其他一些類型的微分方程應該也可以通過變量代換法進行求解，限于篇幅，筆者不再贅述。

1.3 常數變易法

1.3.1 非齊次線性微分方程

1.3.2 伯努利微分方程[11]

1.4 分項組合法[12]

分項組合就是把每一項都分開，然后觀察其中的每一項，先把那些本身就已經構成全微分的項分出來，再把剩下的所有項湊成全微分，這種方法也叫湊分法。

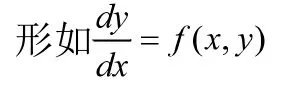
的方程可以寫成一階微分方程的形式：

當方程的左邊正好是某個二元函數的全微分時，該方程稱為恰當微分方程。某方程為恰當微分方程的充要條件是：

我們在判斷所需求解的方程為恰當微分方程之后，便可以通過分項組合的方法來進行求解。

1.5 積分因子法