基于MATLAB的行走機構設計與優(yōu)化

任軍輝 穆龍濤 權 超

（陜西工業(yè)職業(yè)技術學院，陜西 咸陽 712000）

0 引言

移動機器人是現(xiàn)代機器人的一個重要分支，行走機構是其能夠實現(xiàn)移動的結構保障。在所有行走機構中，連桿機構因結構簡單、低副能承受較大的載荷、具有豐富的運動軌跡，能很好地實現(xiàn)移動機器人行走步態(tài)的要求［1］。平面鉸鏈四桿機構是最簡單，也是應用最廣泛的連桿機構，可將其看作一個Ⅱ級桿組連接到原動件和機架上。只要在平面四桿機構上施加一個原動機就可實現(xiàn)復雜的平面運動軌跡［2］。在實際應用中，對行走機構的要求不同，可在四桿機構的基礎上增加桿組，從而設計出較為復雜的多連桿系統(tǒng)［3］，圖1為六桿機械腿結構示意圖。

圖1 六桿機械腿結構拆分

對連桿機構進行設計的方法有作圖法和解析法［4］。作圖法是按照一定的比例尺，用幾何作圖的方式來求解連桿機構的尺寸參數(shù)，該方法較為簡單直觀、高效，但求解精度不高，對較為復雜的連桿系統(tǒng)求解較為困難；解析法是通過建立機構運動要求和機構尺寸參數(shù)間的解析方程式，并根據(jù)已知條件來求解出連桿的尺寸參數(shù)，且求解精度高。隨著計算機技術的發(fā)展，解析法的求解更加方便。MATLAB提供了強大的數(shù)學計算能力，將研究的平面機構放于笛卡爾坐標系中，利用坐標矢量關系來建立求解表達式，即可實現(xiàn)對連桿機構的精確求解與優(yōu)化［5-7］。

1 行走機構方案

一種基于連桿機構的四足機器人行走機構如圖2所示，左右兩側的行走結構完全一致，但在運動狀態(tài)上存在180°的相位差，可實現(xiàn)交替配合。每一側機構中，前肢和后肢結構都是相似的平面四桿機構，通過曲柄共用一個電機。因此，在對其進行分析時，選取一側的前肢結構對其進行分析與優(yōu)化，其機構運動簡圖如圖3所示。

圖2 四足行走機構

圖3 機構運動簡圖

各桿件的尺寸為AB=200 mm、BC=700 mm、CD=700 mm、AD=1 000 mm。平面四桿機構曲柄存在的條件見式（1）。

式中：LAB為AB桿件的長度；LAD為AD桿件的長度；LBC為BC桿件的長度；LCD為CD桿件的長度。由圖3可知，最短桿AB為曲柄，該四桿機構屬曲柄搖桿機構。運動過程如下：AB桿件為原動件，電機通過減速裝置來帶動曲柄作整周轉動，連桿為執(zhí)行構件，P點為末端點，連桿上的某位置作高低起伏的復雜軌跡運動，從而實現(xiàn)與地面接觸及抬起前進的行走動作。

2 機構運動和力分析

2.1 機構數(shù)學模型建立

為了能利用矢量來表示機構的幾何關系，將四桿機構放置于平面直角坐標系中進行研究，如圖4所示。四桿機構的四條邊可構成一個封閉的圖形，用矢量來表示每一段，即在封閉圖形ABCD中，存在的矢量方程見式（2）。

式中：AB為桿AB對應的平面矢量；BC為桿BC對應的平面矢量；AD為桿AD對應的平面矢量；DC為桿DC對應的平面矢量。

為了便于求解導數(shù)，式（2）可用復數(shù)的形式來表示，見式（3）。

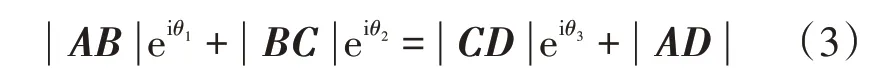
式中：|AB|、BC、|CD|、|AD|分別為AB桿、BC桿、CD桿和AD桿的長度；θ1，θ2，θ3分別為AB桿、BC桿、CD桿與水平方向的夾角（見圖4）。

圖4 行走機構的數(shù)學模型

其中，θ1隨時間的變化規(guī)律就是曲柄的運動規(guī)律，待分析的變量包括其余桿件的角度，可利用MATLAB來求解式（3），以及角度相對時間求一階導、二階導，從而分析各桿件的位置、速度和加速度。

2.2 運動分析

在已知曲柄AB為主動件勻速轉動的前提下，分析其余桿件的位置、速度和加速度的變化情況。由于平面四桿機構的自由度為1，在只有一個原動件的前提下，機構具有確定的運動。P點為連桿BC延長線上的一點，根據(jù)BC桿的運動規(guī)律可求出P點的運動情況。

對式（3）兩側同時求時間的一階導數(shù)，見式（4）。

式中：ω1、ω2和ω3分別為AB桿、BC桿和CD桿的角速度。

為了便于MATLAB的編程求解，用矩陣的形式來表示速度方程，見式（5）。

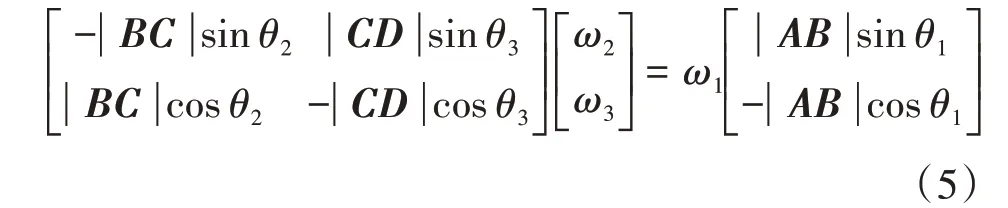
對式（3）兩側同時求時間的二階導數(shù)，或對式（4）兩側同時求時間的一階導數(shù)，得到加速度的方程式，見式（6）。

式中：α2、α3分別為桿BC、桿CD的角加速度。

根據(jù)計算結果，連桿和搖桿的運動規(guī)律如圖5所示。

由圖5可知，當曲柄轉角分別為135°和330°時，CD桿的角速度達到最大值75 rad/s；當曲柄轉角在27°和240°附近時，連桿BC達到最大角速度75 rad/s。在每一個運動周期中，連桿BC和搖桿CD的加速度波動范圍分別為-2.2×104～1.4×104rad/s2、-1.5×104～2.2×104rad/s2。

圖5 行走機構運動分析曲線

2.3 力分析

在運動分析的基礎上，當桿件質量、質心位置、轉動慣量以及執(zhí)行件的工作阻力矩已知，可借助MATLAB軟件來計算運動副上的受力，以及原動機所需的平衡力矩。對活動構件i進行受力分析，并根據(jù)受力分析來建立平衡方程，見式（7）。

式中：Si為質心；MSi為對質心Si的力矩；Fx為水平方向的作用力；Fy為垂直方向的作用力。

在行走機構中，對3個可移動的桿件可建立9個平衡方程，利用MATLAB進行求解，對工作阻力矩為100 N、桿件線密度為10 kg/m的案例進行分析，得到四桿機構C點轉動副的受力和曲柄AB平衡力矩，如圖6所示。

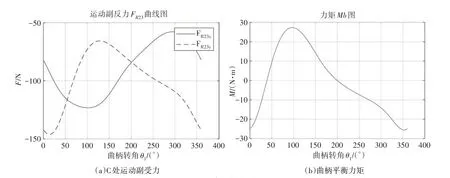
圖6 行走機構力分析

3 行走機構優(yōu)化設計

通過以上分析可以看出，連桿上的點的運動軌跡不盡相同，在圖3中，行走機構末端執(zhí)行點是連桿BC延長線上的一點，為了使行走機構具有良好的傳力性能和越障能力，希望P點的運動軌跡能通過（1 200，-920）、（1 100，-900）、（900，-880）、（800，-910）、（700，-930）這5個點，以這5個點所在的曲線為理想曲線，根據(jù)數(shù)學模型可求解出軌跡上最接近理想曲線的連桿上某點位置，并將其作為P點的實際位置，從而實現(xiàn)對連桿機構的優(yōu)化。目標函數(shù)見式（8）。

式中：(xPi，yPi)、(xi，yi)分別為理想曲線上的坐標點和P點軌跡上的坐標點。

由于P是實際構件上的一點，因此可以是BC線段外的點，但其與連桿是同一個構件。可用BP以及BP和BC之間的夾角θ來表示P點在實際連桿上的位置。優(yōu)化的約束條件見式（9）。

式中：γ為傳動角；γmin和γmax分別為傳動角的最小值和最大值；|AB|、|BC|、|CD|、|AD|分別為AB桿、BC桿、CD桿和AD桿的長度。

由此來設計各桿長度以及P點在連桿上的位置。根據(jù)MATLAB的計算結果在三維建模軟件中進行建模，如圖7所示，即BP=633 mm、θ=13.4°。

圖7 優(yōu)化后的結構即軌跡線

4 結語

本研究基于MATLAB的編程與強大計算能力，使用解析法對連桿行走機構進行運動和受力分析，并在此基礎上，以末端軌跡為目標，對連桿進行優(yōu)化，得出末端執(zhí)行點的具體位置，使連桿行走機構具有良好的傳力和越障性能，從而為精確分析和連桿機構設計提供參考。