以勾股定理的三維推廣為主線的類比推理教學(xué)研究

［摘? 要］ 文章首先闡明了類比推理的重要性以及勾股定理的三維推廣，根據(jù)勾股定理三維推廣中蘊(yùn)含的類比推理，創(chuàng)新地給出以勾股定理的三維推廣為主線的類比推理教學(xué)設(shè)計(jì)，為高中數(shù)學(xué)教師進(jìn)行核心素養(yǎng)教學(xué)提供參考.

［關(guān)鍵詞］ 類比推理；勾股定理；三維推廣

類比推理的重要性

邏輯推理是高中數(shù)學(xué)核心素養(yǎng)之一，主要包括兩類：一類是從特殊到一般的推理，推理形式主要有歸納、類比；一類是從一般到特殊的推理，推理形式主要是演繹. 類比是其中一種重要的推理形式.

類比推理具體的含義是指根據(jù)兩個(gè)（或兩類）對(duì)象之間的一些屬性相同或相似，推測(cè)另一些屬性亦相同或相似的推理方法.

類比推理對(duì)于發(fā)現(xiàn)數(shù)學(xué)事實(shí)、發(fā)現(xiàn)解題思路、實(shí)現(xiàn)數(shù)學(xué)創(chuàng)造具有重要作用.類比推理能夠幫助學(xué)生自主構(gòu)建新知識(shí)，快速到達(dá)相應(yīng)知識(shí)的目標(biāo)層次；同時(shí)，類比推理可以將碎片化的知識(shí)連線成網(wǎng)，使知識(shí)之間的內(nèi)在邏輯關(guān)系清晰明了，實(shí)現(xiàn)對(duì)數(shù)學(xué)知識(shí)的系統(tǒng)化整理.

勾股定理三維推廣的解析

立體圖形中廣泛使用的兩點(diǎn)距離公式可以看作是二維勾股定理的兩次疊加使用，實(shí)現(xiàn)從二維到三維的拓展.同樣，空間中的距離問(wèn)題可以轉(zhuǎn)化為平面的距離問(wèn)題，實(shí)現(xiàn)從平面到立體的拓展. 為此，1981年美國(guó)桑托將二維勾股定理推廣至三維空間；德加于1783年向巴黎科學(xué)院提出了一個(gè)稱為“德加定理”的勾股定理的推廣定理，該定理即為現(xiàn)在熟知的三維面積勾股定理.

（1）勾股定理的推廣定理1（記為“定理1”）：

定理1：直角三角形斜邊上的一個(gè)直邊形，其面積等于直角邊上兩個(gè)與之相似的直邊形面積之和.

該定理出自歐幾里得《幾何原本》，這實(shí)際上是對(duì)勾股定理的一個(gè)證明. 雖然該證明只是停留于平面勾股定理，但是為勾股定理的推廣提供了思路方法，許多空間勾股定理的來(lái)源正是這個(gè)推廣定理.

（2）勾股定理的空間推廣（記為“推論”）：

推論：空間中，以直角三角形的三邊為對(duì)應(yīng)棱作相似多面體，則斜邊上的多面體的表面積等于直角邊上兩個(gè)多面體表面積之和.

（3）三維空間的（面積）勾股定理（記為“定理2”）：

定理2：直角四面體的底面面積的平方，等于三個(gè)斜面的面積的平方之和.

勾股定理三維推廣中的類比推理

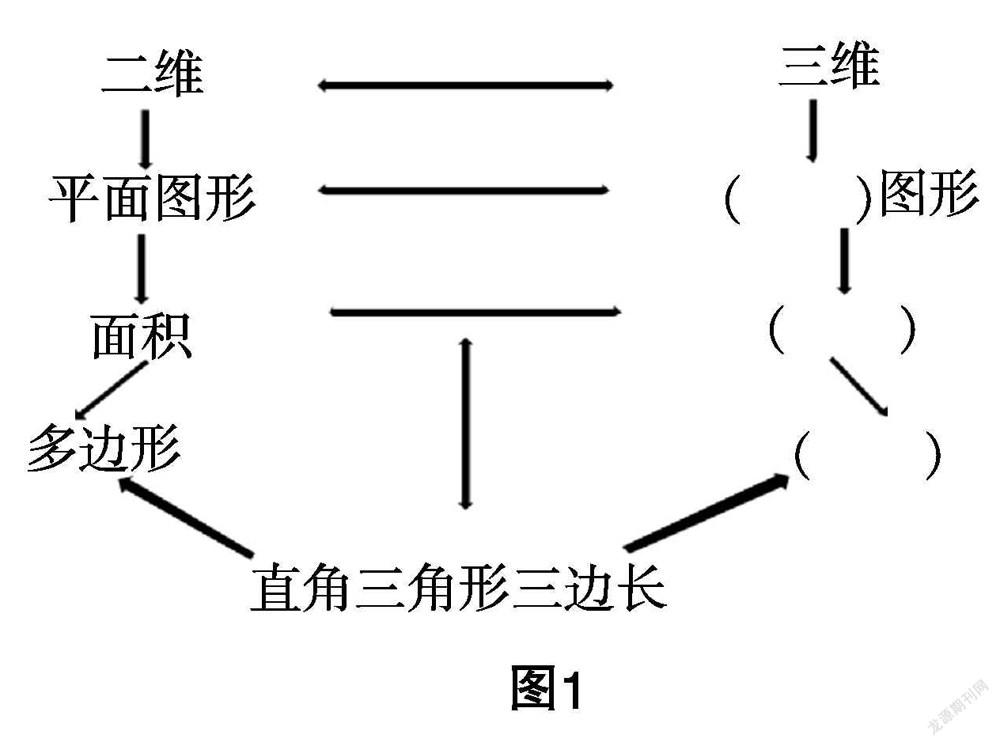
？搖 從定理1到推論，其實(shí)是將一個(gè)直角三角形從二維平面放到三維空間的過(guò)程，需要將二維平面中的一些元素與三維空間中的一些元素進(jìn)行合理類比得到，比如將二維平面中直邊形的面積對(duì)應(yīng)到三維空間中，應(yīng)該是表面積而非體積.

從推論到定理2，是將空間中的直角三角形從一個(gè)到多個(gè)的變化，需要將三角形的特征與多個(gè)三角形組成的四面體的特征進(jìn)行合理類比得到，比如三角形由三邊組成，對(duì)應(yīng)到三個(gè)直角三角形面圍成的一個(gè)封閉立體圖形.

勾股定理三維推廣中蘊(yùn)含著豐富的類比推理，對(duì)勾股定理的推廣研究具有重要價(jià)值. 因此當(dāng)學(xué)生學(xué)習(xí)完空間幾何的有關(guān)知識(shí)后，讓其了解勾股定理的三維推廣，對(duì)培養(yǎng)學(xué)生的類比推理能力具有非常良好的效果.

勾股定理三維推廣教學(xué)設(shè)計(jì)

本節(jié)課內(nèi)容針對(duì)的是高二年級(jí)學(xué)習(xí)完立體幾何、空間向量的學(xué)生，教材可參考人教版選修2-2的“合情推理”章節(jié).

1. 教學(xué)目標(biāo)

知識(shí)與技能目標(biāo)：了解定理1，理解推論，掌握定理2的具體內(nèi)容，會(huì)簡(jiǎn)單應(yīng)用定理2，理解定理2的證明.？搖

過(guò)程與方法目標(biāo)：通過(guò)了解數(shù)學(xué)史中定理1的內(nèi)容和證明，類比推廣得到推論的內(nèi)容及球體情況的證明，經(jīng)歷從定理1和二維勾股定理的數(shù)量關(guān)系類比推理德加提出的定理2的過(guò)程，提高類比推理能力，體會(huì)類比推理思想方法.

情感態(tài)度與價(jià)值觀目標(biāo)：讓學(xué)生了解歐幾里得和《幾何原本》，體會(huì)古代數(shù)學(xué)家的智慧；通過(guò)學(xué)生自己類比推理得到“德加定理”，讓學(xué)生領(lǐng)悟數(shù)學(xué)類比思想的應(yīng)用，感受數(shù)學(xué)思想的奇妙；同時(shí)，通過(guò)從二維平面的推廣到三維空間的推廣的幾何直觀，讓學(xué)生體會(huì)數(shù)學(xué)定理的奇妙和簡(jiǎn)潔.

2. 教學(xué)重難點(diǎn)

重點(diǎn)：類比推理思想方法，兩個(gè)定理和一個(gè)推論的內(nèi)容.

難點(diǎn)：定理2的應(yīng)用，以及類比推理的應(yīng)用.

3. 教學(xué)過(guò)程

環(huán)節(jié)1：?jiǎn)栴}引入

（1）教師活動(dòng).

問(wèn)題1：大家學(xué)習(xí)過(guò)的勾股定理公式是什么？有同學(xué)知道哪些古代數(shù)學(xué)家對(duì)勾股定理進(jìn)行過(guò)證明嗎？怎么證明的？

教師根據(jù)學(xué)生的回答，在黑板上寫上數(shù)學(xué)家的名字，并說(shuō)明證明勾股定理有許多方法.

問(wèn)題2：同學(xué)們知道歐幾里得是如何證明勾股定理的嗎？

教師展示歐幾里得是如何證明勾股定理的，并介紹歐幾里得和《幾何原本》.

問(wèn)題3：歐幾里得證明勾股定理的方法不是直接得到的，是通過(guò)什么間接得到的？能否將這種證明方法歸納為一句話：什么證明什么？

（2）學(xué)生活動(dòng).

學(xué)生思考并回答教師的三個(gè)問(wèn)題，跟隨教師的思路，認(rèn)識(shí)歐幾里得和《幾何原本》，以及歐幾里得證明勾股定理的方法，思考問(wèn)題3并嘗試自己寫一句話來(lái)表達(dá).

設(shè)計(jì)意圖：三個(gè)問(wèn)題啟發(fā)并引導(dǎo)學(xué)生進(jìn)行思考，在思考中帶領(lǐng)學(xué)生跟隨歐幾里得的腳步，從二維勾股定理逐漸推廣，為三維勾股定理的引出做鋪墊；同時(shí)通過(guò)問(wèn)題3歸納歐幾里得證明勾股定理的方法的本質(zhì)，有助于學(xué)生理解歐幾里得定理的推廣. 以歐幾里得為主線，讓學(xué)生了解數(shù)學(xué)史、體會(huì)古代數(shù)學(xué)家的智慧.

環(huán)節(jié)2：新知探究

第一部分——定理1：

（1）教師活動(dòng).

歐幾里得的證明方法的特點(diǎn)是：用面積關(guān)系證明勾股定理的數(shù)量關(guān)系. 根據(jù)這兩個(gè)關(guān)系的互相推導(dǎo)，歐幾里得在《幾何原本》中對(duì)勾股定理進(jìn)行了推廣：

定理1：直角三角形斜邊上的一個(gè)直邊形，其面積等于直角邊上兩個(gè)與它相似的直邊形面積之和.

教師請(qǐng)學(xué)生歸納歐幾里得的證明方法的特點(diǎn)，用一句話概括定理1的特征：什么推廣什么？（特征：數(shù)量關(guān)系推廣面積關(guān)系）？搖

（2）學(xué)生活動(dòng). 對(duì)照教師給出的特征與自己歸納的特征，體會(huì)歐幾里得的證明方法的本質(zhì).

設(shè)計(jì)意圖：通過(guò)讓學(xué)生了解定理1的內(nèi)容，自主歸納定理1的特征，使學(xué)生理解定理1的來(lái)源. 同時(shí)，讓學(xué)生自主歸納定理1的特征，為推論的類比推理做好鋪墊，讓學(xué)生初步體會(huì)類比推理的過(guò)程.

第二部分——推論：

（1）教師活動(dòng).

得到定理1的特征后，教師給出符合定理1的一個(gè)特例——圓，雖然圓不屬于直邊形，但定理1依然成立. 教師給出以直角三角形三邊長(zhǎng)為直徑的三個(gè)圓，并給出證明過(guò)程：

教師提問(wèn)：“類比歐幾里得的推廣，將直角三角形放到空間考慮，將定理1中直邊形或圓的面積關(guān)系推廣到空間，那么此時(shí)圖形的面積關(guān)系會(huì)變成什么呢？”讓學(xué)生進(jìn)行思考并完成下面的填空：

教師巡視并展示填空答案，重點(diǎn)講解“面積”對(duì)應(yīng)的空格為何是“表面積”而非“體積”；教師講解“面積”對(duì)應(yīng)“表面積”后，讓學(xué)生根據(jù)這個(gè)類比框架，歸納從二維平面推廣至三維空間的特征——從面積關(guān)系推廣至表面積關(guān)系，讓學(xué)生根據(jù)定理1的描述和三維空間的推廣特征，自主得到推論：

推論：空間中，以直角三角形的三邊為對(duì)應(yīng)棱作相似多面體，則斜邊上的多面體的表面積等于直角邊上兩個(gè)多面體表面積之和.

同樣仿照定理1中的特殊圖形——圓，讓學(xué)生自主證明推論中多面體變成球的情況，教師展示學(xué)生的答案并進(jìn)行講解.

（2）學(xué)生活動(dòng).

首先學(xué)習(xí)定理1中的特例——圓，理解證明過(guò)程. 思考并填空，填空過(guò)程中理解類比推理是如何進(jìn)行的，聽(tīng)完教師講解填空答案后了解類比推理的概念. 讓學(xué)生自主思考后寫出推論的內(nèi)容，并根據(jù)定理1中圓的證明，類比證明推論中多面體變成球的情況. 在課后思考并寫下以直角三角形三邊為棱所作正方體表面積的關(guān)系的證明，對(duì)比它與球的區(qū)別.

設(shè)計(jì)意圖：學(xué)習(xí)定理1的特例和證明，讓學(xué)生體會(huì)定理1的證明思路，為推論的證明做好鋪墊. 讓學(xué)生填空，完成二維到三維的類比過(guò)程，填空過(guò)程中學(xué)習(xí)類比推理是怎樣進(jìn)行的，特別是由面積類比到表面積，讓學(xué)生明白類比推理需要根據(jù)特征尋找合適的類比對(duì)象，真正理解并掌握類比推理思想方法.

讓學(xué)生自主得到推論，加深學(xué)生對(duì)推論的理解和掌握. 同時(shí)，通過(guò)剛學(xué)習(xí)的以直角三角形三邊為棱所作正方體表面積的關(guān)系的類比推理，深刻體會(huì)類比推理思想方法.

第三部分——定理2：

（1）教師活動(dòng).

教師：“推論從勾股定理出發(fā)，將以直角三角形的三邊為棱所作多邊形的面積關(guān)系推廣到空間中的表面積關(guān)系.勾股定理表述的是直角三角形及其邊長(zhǎng)的數(shù)量關(guān)系，它有一個(gè)重要元素即直角三角形，立體空間中哪一類立體圖形可以作為直角三角形的類比對(duì)象？”

教師以引導(dǎo)方式帶領(lǐng)學(xué)生按照序號(hào)，完成下面的填空，讓學(xué)生找到立體空間中適合作為直角三角形類比對(duì)象的立體圖形——直角四面體.

在得到直角四面體的特征后，教師讓學(xué)生類比勾股定理的結(jié)構(gòu)猜想直角四面體的性質(zhì)：“1783年，一位叫德加的人向巴黎科學(xué)院提出了一個(gè)定理——‘德加定理’. ‘德加定理’就是大家類比得到的關(guān)于直角四面體的勾股定理的推廣定理. 大家嘗試猜想一下，能否得到300多年前的這個(gè)定理呢？”

教師講解直角四面體的性質(zhì)，得到定理2，即三維空間的（面積）勾股定理，并用數(shù)學(xué)語(yǔ)言敘述定理2，給出嚴(yán)謹(jǐn)?shù)陌鍟?/p>

定理2：直角四面體的底面面積的平方，等于三個(gè)斜面的面積的平方之和.？搖

（2）學(xué)生活動(dòng).

大膽猜想直角四面體的性質(zhì)，抓住勾股定理三邊關(guān)系的特征，嘗試寫出直角四面體底面與斜面的面積關(guān)系的式子. 理解定理2，在紙上記下定理2的數(shù)學(xué)語(yǔ)言描述.

設(shè)計(jì)意圖：從另一個(gè)角度推廣勾股定理，體會(huì)勾股定理三維推廣的多角度的推廣方法，同時(shí)自主運(yùn)用類比推理的思想方法掌握其精髓，體會(huì)數(shù)學(xué)文化中類比思想的奇妙.

提問(wèn)直角四面體的特征讓學(xué)生注意到類比過(guò)程中尋找合適類比對(duì)象的重要性，猜想直角四面體的性質(zhì)能夠激發(fā)學(xué)生的創(chuàng)造性思維；同時(shí)通過(guò)介紹發(fā)現(xiàn)定理2的歷史，讓學(xué)生帶有發(fā)現(xiàn)“數(shù)學(xué)家發(fā)現(xiàn)的定理”的一種成就心理. 學(xué)生理解定理2后，給出數(shù)學(xué)語(yǔ)言描述讓學(xué)生明白數(shù)學(xué)語(yǔ)言的簡(jiǎn)潔和嚴(yán)謹(jǐn).

環(huán)節(jié)3：新知應(yīng)用

（1）教師活動(dòng).

教師給出以下例題，讓學(xué)生應(yīng)用定理2進(jìn)行解答：已知三棱錐P-ABC的三個(gè)側(cè)面互相垂直，它們的三個(gè)側(cè)面面積都是2，求P到平面ABC的距離.

（2）學(xué)生活動(dòng).

？搖思考例題的解答方法，應(yīng)用定理2自主解答例題.

設(shè)計(jì)意圖：給出例題讓學(xué)生鞏固定理2，同時(shí)在學(xué)生解題過(guò)程中體會(huì)類比推理的過(guò)程.

環(huán)節(jié)4：課堂小結(jié)

（1）教師活動(dòng).

教師總結(jié)類比推理的流程：

教師以提問(wèn)的形式，帶領(lǐng)學(xué)生回顧從二維勾股定理推廣到三維空間（面積）勾股定理的過(guò)程，幫助學(xué)生鞏固、內(nèi)化三個(gè)定理.

（2）學(xué)生活動(dòng).

根據(jù)流程圖回顧類比推理的過(guò)程，同時(shí)根據(jù)教師的提問(wèn)思考和回憶勾股定理三維空間的推廣過(guò)程.

設(shè)計(jì)意圖：通過(guò)課堂小結(jié)讓學(xué)生回顧整個(gè)推廣過(guò)程以及類比推理的過(guò)程，讓學(xué)生更深刻地理解類比推理的含義、流程.

總結(jié)

“如何在課堂教學(xué)中培養(yǎng)核心素養(yǎng)”，一直是高中數(shù)學(xué)教學(xué)一個(gè)熱議的話題，勾股定理的三維推廣雖不屬于最新版教材教學(xué)內(nèi)容范圍，但二維平面的勾股定理是學(xué)生非常熟悉的內(nèi)容，從二維到三維的推廣是類比推理思想非常明顯的一個(gè)過(guò)程，因此當(dāng)學(xué)生高二年級(jí)學(xué)習(xí)完空間立體幾何后，教師進(jìn)行勾股定理三維推廣教學(xué)，能夠幫助學(xué)生體悟類比推理思想方法，對(duì)于培養(yǎng)學(xué)生邏輯推理素養(yǎng)具有重要意義.

作者簡(jiǎn)介：黃雅萱（2000—），本科學(xué)歷，研究方向：數(shù)學(xué)與應(yīng)用數(shù)學(xué)（師范）.