基于Contig的單面基因組片段填充問題研究
柳 楠,朱永琦,李勝華,崔曉宇
(山東建筑大學 計算機科學與技術學院,山東 濟南 250101)
0 引 言
隨著二十世紀三大科學計劃之一的人類基因組計劃的實施,大量的生物學數據有待處理[1-4],如何利用計算機建模、仿真等技術去提取其中有用的數據,進而研究其中所蘊含的生物學意義,對計算機科學技術來說是一項嚴峻的挑戰[5-6]。因此在二十世紀提出了一門新興交叉學科—計算生物學。計算生物學運用數學、計算機和生物學相關理論解決生物學問題,已經成為目前最活躍的研究領域之一[7-9]。
基因組片段填充問題[10-12]是計算生物學極其經典的問題之一,其中含重復基因的基因組片段填充問題已經被證明為NP-完全問題[13-14],如何優化基因組片段填充近似算法是近些年來的討論熱點。依據基因樣本序列中是否含有重復基因,將該基因組填充問題分為含重復基因的基因組片段填充問題和無重復基因的基因組片段填充問題;或依據基因樣本序列不完整數量,將該基因組填充問題分為單面基因組片段填充和雙面基因組片段填充,其中一條序列完整,另一條序列缺失,稱為單面基因組序列,兩條基因序列均為不完整的,則為雙面基因組序列[15]。
該文重點討論單面重復基因組片段填充問題。Munoz和D. Sankoff等人[12-13]首次提出了基于最小重組距離(DCJ距離)的單面基因組填充方法,使用斷點圖設計了多項式時間算法,并證明了基于DCJ距離的單面基因組片段填充算法是多項式可解的。對于單面無重復基因組片段填充問題,H. Jiang等人提出了使用DCJ距離或斷點距離為度量的算法,并證明了其是多項式可解的[14];對于含重復基因的基因組片段填充問題,H. Jiang等人證明了其是NP-完全的,并提出了4/3-近似算法[14-16]。隨后N. Liu等人采用局部優化和貪婪算法將該類問題近似度改善到1.25[17-18];J. Ma等人采用非盲局部搜索策略將該類問題近似度進一步改善到1.2[19-20]。
在許多應用中,基因組序列通常被定義為一系列連續的片段重疊群(contig)[21],其中任何一個contig都不能被破壞,缺失基因的插入只能在contig的兩端執行。在此約束下,當不存在重復基因時,單面基因組片段填充問題是多項式可解的;當存在重復基因時,H. Jiang等人通過最大化公共鄰接證明了該類問題是NP-完全的,并提出了一個近似值為2的近似算法[22-23]和一個雙參數的FPT算法[22](k,公共鄰接數,d,基因最大重復數);L. Bulteau等人給出了一種基于最大鄰接數和最小斷點距離的k-Mer參數的FPT算法[24];Q. Feng等人通過構造輔助圖和二次尋找最大匹配給出了2.57-近似算法[25]。
該文的主要工作有以下三個方面:系統歸納了基于contig的單面基因組片段填充問題的現有算法并通過實例實現了算法,有助于讀者對此類問題的進一步了解;在技術應用和時間復雜度等方面對現有算法做了對比,并分析了該些算法存在的一些弊端;分析接下來研究工作中面對的挑戰和可能的解決方案。
1 相關定義
該文只關注基于contig的單面基因組片段填充算法,但其結果可以推廣到多染色體或環狀基因組。
首先,給出一些必要的定義。不失一般性,假設所有的基因和基因組都由無符號的字母和整數組成,給定一個集合Σ和一個基因序列S,使用c(S)表示基因序列S中所有符號的集合。如果Σ中的符號在基因序列S中出現且只出現一次,則稱S是Σ上的一個排列,否則稱為序列。對于Σ中的任意兩個符號x,y,如果基因序列S至少包含{xy,yx}中的任意一個子集,那么則稱x,y在S中鄰接,令P(S)為S中所有鄰接的集合。設A和B是Σ中的兩個基因序列,A={a1a2…an},B={b1b2…bm}。對于P(A)中的任意一個鄰接aiai+1和P(B)中的任意一個鄰接bjbj+1,如果aiai+1=bjbj+1(或aiai+1=bj+1bj),則稱aiai+1與bjbj+1構成了公共鄰接,a(A,B)表示A和B的公共鄰接集合,同時稱(aiai+1,bjbj+1)為一個匹配對。如果P(A)和P(B)中不存在aiai+1=bjbj+1(或aiai+1=bj+1bj),則稱aiai+1相對于bjbj+1構成了斷點,bp(A,B)和bp(B,A)分別表示A和B的斷點集合,如圖1所示。
定義一個基因組序列是由一系列contig構成的,且contig內部不能插入缺失基因,即S=
下面具體給出One-Sided-SF-max問題的概念:
定義1:One-Sided-SF-max問題。
輸入:一個完整的基因組序列G和一個不完整的基因組序列S,其中S=
輸出:將X=c(G)-c(S)≠?插入S得到S',使得|a(S',G)|最大。
2 One-Sided-SF-max問題
One-Sided-SF-max問題已經被證明為NP-完全的[22],此類問題不能在有效時間內求出精確解,因此設計近似算法更具有實際意義。本節主要對One-Sided-SF-max問題進行簡要介紹,概括分析了國內外經典的三種算法:2-近似算法、2.57-近似算法以及k-Mer算法。
2.1 One-Sided-SF-max問題的2-近似算法
該算法由H. Jiang等人提出,主要使用了貪婪和最大匹配的思想來實現基于contig的單面基因組片段填充。首先在該算法中給出以下定義:對于基因序列S=
定義缺失基因集合X中有一個長度為n的子串,如果插入到slot <βi,αi+1>中(1≤i≤m-1),產生n+1個新公共鄰接,稱子串為n-Type-1類型串。同樣的,產生n個新公共鄰接,稱為n-Type-2類型串;產生n-1個新公共鄰接,稱為n-Type-3類型串。算法大體流程如下:
(1)計算缺失基因集合X=c(G)-c(S);
(2)對于缺失基因集合,采用貪婪策略將1-Type-1類型串插入到相應的slot中,并將該slot鎖定,不允許其他缺失基因插入;
(3)構造二分圖并求其最大匹配,將1-Type-2類型串插入到可構成外部鄰接的slot處,并對該slot進行更新:如果xj插入到slot ?ai前面,那么將此slot更新為?xj,如果?xj插入到slotβi?后面,那么將此slot更新為xj?;
(4)以步驟2后的缺失基因為頂點構造多重圖:若x∈X,y∈X且xy為G中一個內部鄰接,那么x和y之間添加一條邊,尋找最大匹配M。對于最大匹配M中的所有匹配對xy,如果x為步驟3中插入的元素,則將y插入到相應slot處使得xy構成鄰接;將其余匹配對xy任意插入到未鎖定slot中,且不能破壞現有鄰接;
(5)在不破壞現有鄰接關系的前提下,將所有剩余缺失基因任意插入到S中未鎖定的slot處;
(6)得到近似解S'。
對于該算法,下面通過一個實例(如圖2所示)來說明算法的執行過程:

(2)搜尋1-Type-2類型串,找到2,d,g為1-Type-2類型串,并以1-Type-2類型串集合和未鎖定slot集合為頂點,構造二分圖,建立的二分圖BG1如圖3所示。

(3)以步驟2之后的剩余缺失基因集合為頂點構造多重圖Q,建立的多重圖Q并求得最大匹配,將a插入到g之前,將7插入到d之后,將52插入到a之前。
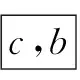
(5)算法結束,得到填充后的基因序列S'=
<52ag4k1acbd21d727>。
以上可以看出,通過此算法可以得到8個新公共鄰接,同時此例的最優解為S*=<2ag4k1acb1d7527d2>,有13個新公共鄰接。

所以,

所以有近似解:
該算法為一個2-近似算法,同時該算法的運行時間主要由步驟2中計算O(n)個頂點的二分圖中的最大匹配以及步驟3中計算O(n)個頂點的多重圖中的最大匹配決定,兩者都需要O(n2.5)個時間,所以2-近似算法的時間復雜度為O(n2.5)。
2.2 One-Sided-SF-max問題的2.57-近似算法
Q. Feng提出的2.57-近似算法繼續考慮了冗余塊對填充過程存在的影響。該算法主要使用了最大匹配算法構造簡單路徑來具體實現基于contig的單面基因組片段填充問題。
首先在該算法中給出以下定義:令F(S)為contigCi的首尾元素集合,F(S)=(α1,β1,…,αm,βm)。如果最大匹配M中有塊xy,xy在最大匹配M中出現的次數稱為xy的指示數。設xy與bp(G,S)中塊ab可構成匹配對(xy,ab),若xy在M中出現次數大于ab在bp(G,S)中出現次數,則稱塊xy為一個冗余塊。定義⊕為對稱差,A⊕B=(AB)∪(BA),令K'為此算法中的兩次最大匹配M1和M2的對稱差,則K'中每個連通分量必為簡單路徑或簡單循環。算法的大體流程如下:
(1)計算缺失基因集合X=c(G)-c(S)和斷點集合bp(G,S);
(2)基于缺失基因集合X、斷點集合bp(G,S)和S中每個contig首尾元素集合F(S)構造一般圖Γ1,尋找最大匹配M1;
(3)對于M1中的任意塊xy,有以下三種情況:如果x和y分別為同一個slot的前后兩端,則合并此相鄰的兩個contig;如果x(或y)屬于F(S),將y(或x)插入相應的slot中使得xy鄰接;如果x和y均不屬于F(S),則將其置于圖H'中頂點。依據以上更新基因序列為S1;
(4)基于G、S1和H',求得斷點集合bp(G,S1)和F(S1);
(5)更新圖H':刪除可與bp(G,S1)中斷點構成匹配對的邊;
(6)基于缺失基因集合X、斷點集合bp(G,S1)和集合F(S1)構造一般圖Γ2,尋找最大匹配M2;
(7)Δ=H'⊕M2;
(8)對于圖Δ中的任意路徑k=p1p2…pt-1pt,判斷其是否為簡單路徑:若為簡單路徑,插入到相應slot中,反之刪除路徑k中任意一條邊得到新的路徑p1p2…pt-1pt,將路徑p1p2…pt-1pt插入到基因序列的最右側;更新基因序列為S2;
(9)統一將c(G)-c(S2)插入到序列S2的最右側;
(10)得到填充完成后的基因序列S'。
下面通過上述2-近似算法的同一個實例(見圖2)來說明算法的執行過程:
(1)計算斷點集合bp(G,S)=<1a,ac,1d,d7,75,52,24,4g,ga,a2,2k,k7,7d,d2>,計算S中每個contig首尾元素集合F(S)=<4,1,c,b,1,1>;
(2)構造圖Γ1:X∪F(S)中的所有元素被視為頂點,對于其中任意兩個元素x,y,如果有x∈X,y∈X或y∈F(S)且存在一個斷點β使得與xy構成一個匹配對,則在x與y之間添加一條邊;如果有x,y∈F(S),假設x在contigC1中且為C1中最后一個元素,y在contigC2中且為C2中第一個元素,C1和C2相鄰且存在一個斷點β使得與xy構成一個匹配對,則在x與y之間添加一條邊。在圖Γ1中尋找最大匹配M1,如圖4所示;
(3)刪除M1中的冗余塊:對于M1中的塊xy,xy與斷點ω可構成匹配對(xy,ω),如果xy在M1中的出現次數大于ω在bp(G,S)中的出現次數,則稱塊xy為冗余塊并將其刪除;
(4)令{α1,α2,…,αr}為M1中刪除冗余塊后剩余塊的集合,H'為{α1,α2,…,αr}中的塊與bp(G,S)中的斷點構成匹配對的集合,則此例中H'={(ac?ac),(d1?1d),(52?52),(g4?4g),(a2?a2),(d2?d2)};


(7)計算X'=c(G)-c(S1)得到缺失基因集合X'=<7,5,2,a,2,7,d,2>,計算S1中每個contig首尾元素集合F(S1)=
(8)計算新的斷點集合bp(G,S1)=
(9)使用構造圖Γ1的同樣方法構造圖Γ2;
(10)如果圖Γ2與圖H'中存在相同邊,則在Γ2中刪除此條邊,此例中,無此類邊;
(11)在圖Γ2中求得最大匹配M2,如圖5所示。
(12)令Δ=H'⊕M2,此例中Δ=(a2,ag,7d);


(15)將剩余缺失基因插入到序列S2的最右側;
(16)得到填充完成后的基因序列S'=
該算法可以得到8個公共鄰接,同時其中一個最優解為<2ag4k1acb1d7527d2>,有13個新公共鄰接。

該算法的近似性能比為2.57。
2.3 One-Sided-SF-max問題的k-Mer近似算法
k-Mer算法從參數化復雜性的角度研究基因組填充問題,相較于H. Jiang等人提出的2-近似算法,主要有以下三個方面的不同:
(1)不再限制插入的基因集合為c(G)-c(S),插入集合可以包含比c(G)-c(S)更多或更少的基因集合;
(2)允許將要插入的字符串數量預先指定為輸入約束,t1為要插入的字符串數量的下限,t2為要插入的字符串數量的上限(t1≤t2);
(3)作為相似性度量依據,不局限于最大化公共鄰接的數量,相反,對于一個預定的參數k,最大化公共k-mers的數目,k值越高,結果越準確。
L.Bulteau等人對于此類問題給出以下定義:對于兩個基因序列G和S,G°S表示二者的串聯。存在一個正整數k,使得ak(G)={S[i,i+k]|i∈[n-k]}為序列G中k-mers的集合,則ak(G,S)=ak(G)∩ak(S)。設S[i]表示S中第i個元素,S[i,j]表示序列S中從位置i到j的基因元素。對于一個完整基因序列G和一個不完整基因序列S,令pk(S,G)=ak(G)ak(S)表示存在于G中但不存在于S中的k-mers集合,并將此類k-mers稱為潛在的公共k-mers。
定義2:k-Mer Scaffold Filling(k-Mer-SF)。
輸入:一個完整的基因組序列G和一個不完整的基因組序列S,其中S=
輸出:找到T'?T,t1≤|T'|且填充后的S'∈S+T',使得|ak(S',G)|最大。
該文給出一個k-Mer-SF實例,在此只舉例說明了k=2和k=3的填充情況(如圖6所示)。
H. Jiang等人提出的2-近似算法和Q. Feng等人提出的2.57-近似算法均為k-Mer-SF中t1=t2=|T|且k=2時的特殊情況,并可在多項式時間O(3·(+m)2)內計算。k-Mer-SF相較于以上兩個近似算法,不再僅僅參考公共鄰接數目的多少,主要使用以下評估參數:k,k-mers的長度;:=ak(S*,G)-ak(S,G),匹配后帶來的額外公共k-mers數目;d,一個基因在G中出現的最大次數;m,S中重疊群的個數;t2,要插入的字符串數量的上限;λ,T中字符串長度的上界。
k-Mer算法主要解決了基于動態規劃如何在2O()·nO()時間內求得近似解并給出其參數為k+的FPT算法。首先使用著色法對k-mers進行分類,β:T→[t2]表示潛在的公共k-mers,β:T→[t2]表示可能插入字符。圖著色后,使用動態規劃算法重建序列S,使得S中有個潛在的公共k-mers轉為已實現的k-mers,在動態規劃過程中逐步找到大小遞增的局部最優解,從左到右依次將缺失基因插入到序列S中,并使用局部優化策略避免一些缺失基因重復插入。
對于k-Mer-SF問題,首先對序列G,S及插入基因集合T做約簡操作。刪除T中多余基因元素,如果T中存在一個基因元素出現次數大于t2,將刪除一個元素;其次,對G中的鄰接關系分類,并只保留潛在公共鄰接,假設x為不出現在S和T中的基因,y為不出現在G中的基因,令P1°x°P2°…°Pq-1°x°Pq替換G且用Ci[1]°y°Ci[|Ci|]表示S。如果有一個潛在鄰接在G中出現次,則在G中刪除一個該鄰接,刪除后若鄰接滿足以下條件之一,則稱為可實現鄰接:
(1)b∈T且c∈T;
(2)存在一個contigCi使得b∈Ci[|Ci|]且c∈T;
(3)存在一個contigCi使得b∈Ci[|Ci|]和c∈Ci[1];
(4)存在一個contigCi使得b∈T且c∈Ci[1]。
建立鄰接圖H=(V,E):令T,G和S中的基因元素作為H中的頂點,如果鄰接bc或鄰接cb均為可實現鄰接,則令兩個頂點b和c相鄰,求得最大匹配M。
令V(M)表示匹配的端點,建立兩個二分圖H1和H2且頂點分別為B:=V(M)和C:=(VV(M))。在H1中,當bc是一個可實現鄰接時,在b∈B和c∈C之間添加一條邊。在H2中,當cb是一個可實現鄰接時,在b∈B和c∈C之間添加一條邊。如果H1中存在頂點b∈B且度數至少為2+m+1,則將鄰接bc從G中移除;如果H2中存在頂點b∈B且度數至少為2+m+1,則將鄰接bc從G中移除,其中c是b的任意鄰接。
完成約簡操作后,這些頂點的數量最多為|V(M)|·2·(2+m+1)。這給出了G中頂點數量的界限,從而給出了實例大小的界限且所有約簡規則可以在多項式時間內執行。
從更廣泛的角度來看,k-Mer-SF考慮了字符串的基本插入問題。事實上,可以將該算法擴展到更一般的情況,即給定一個字符串G和一個部分字符串S,完成部分字符串S的插入得到新的字符串S',使得G和S'的相似度最優,因此其包含了H. Jiang等人的問題作為特例。
3 One-Sided-SF-max問題的總結
該文發現2-近似算法沒有考慮斷點對填充過程的影響和長度大于1的缺失串的插入情況,2.57-近似算法則沒有考慮n-Type-3類型串的插入情況,k-Mer算法也僅僅介紹了固定基因子串長度的一般處理情況,然而不同長度以及不同類型串的插入都會對公共鄰接數造成影響,從而影響到算法近似比。

序列中存在連續長缺失基因串,在完成1-Type-1類型串的插入后,假設存在可構成n-Type-1類型串的缺失基因串a1a2…an,如若按照2-近似算法中分別處理,則該缺失基因串中1-Type-1類型串被破壞,有以下2種情況:
(1)最多有n個1-Type-2類型串,產生n個鄰接;
(2)最少有2個1-Type-2類型串,剩余為n-Type-3類型串,產生2個鄰接。
產生鄰接數k為2≤k≤n,若將其合并后插入基因序列中,則會產生n+1個鄰接。以上證明合并插入n-Type-1類型串具有更優效果。
在處理n-Type-2類型串時,假設存在可構成n-Type-2類型串的缺失基因串b1b2…bn,如若按照2-近似算法分別處理,則該缺失基因串中n-Type-2類型串被破壞,有以下2種情況:
(1)最多有2個1-Type-2類型串,同時bi(2≤i≤n-1)均可與其相鄰缺失基因bi-1或bi+1(2≤i≤n-1)構成內部鄰接,產生n個鄰接;
(2)最少有1個1-Type-2類型串,同時剩余n-1個缺失基因均為n-Type-3類型串,產生1個鄰接;產生鄰接數k為1≤k≤n,如若將其合并后插入基因序列中,會產生n個鄰接。以上證明合并插入n-Type-2類型串具有更優效果。
對于2.57-近似算法,雖然n-Type-3類型串會產生n-1個鄰接,但是如果不對其進行處理,任其插入未鎖定的slot,存在破壞已有鄰接的可能,其中最多會破壞2個鄰接,n-Type-3類型串產生鄰接數k為n-3≤k≤n-1,明顯降低最后的填充效率,所以對其進行插入處理十分必要。
k-Mer算法固定了基因子串的長度,2-近似算法就是一個特例,其固定長度為2的公共鄰接數目作為算法性能參考依據,以上也證明了此時并不是最優算法,進而說明了基因填充過程中限制基因子串長度存在影響近似性能比的可能。
4 總結與展望
重點介紹了基于contig的單面重復基因組片段填充問題的研究現狀。對該些算法在近似性能比等方面做出了詳細的對比(見表1),直觀地看出各個算法現存在的一定不足,說明此類算法仍有改進空間,同時提出了該類問題的改進思路。

表1 三種算法分析比較
4.1 面臨的挑戰
(1)現有算法依賴于公共鄰接數目,鄰接的定義沒有考慮基因序列不存在逆序關系的情況,因此存在兩個基因序列的鄰接均為公共鄰接但二者完全不相似的情況,不利于后續對算法近似比的研究。
(2)現有算法對度量依據的選擇較少,并過度依賴于最大匹配算法,因此對此類問題的研究較為片面。
4.2 前景展望
針對目前單面重復基因組片段填充問題的研究工作,發現基因組填充問題有以下發展前景。
(1)目前One-Sided-SF-max問題的最佳性能近似比為2,日后還需要進一步優化。
(2)現有算法均是在最大化鄰接基礎上考慮其近似比,基于最小斷點數層面有待研究。
(3)雙面基因組填充問題也被證為NP-完全的,但沒有提出近似比算法,此類算法可推廣到雙面基因組填充問題,有利于雙面此問題的近似比優化。

