不同定權模型對GPS/BDS/Galileo短基線相對定位的影響分析

崔 琛

（1.河南省有色金屬地質礦產局第七地質大隊，河南 鄭州 450016）

全球導航衛星系統（GNSS）是當前各方面建設不可或缺的服務系統。在各國不斷建設發展自己的導航定位系統的同時，如何提升導航定位精度是當前研究的重點問題[1-3]。對各項誤差改正模型進行改進以及正確選擇定權方式均可有效提升定位精度[4-6]。相對定位是一種精密定位技術，尤其是短基線相對定位技術應用十分廣泛；隨著GNSS的蓬勃發展，多系統組合相對定位將是今后發展的趨勢，而正確選擇短基線相對定位定權模型是保證短基線相對定位精度的重要策略[7-8]。

對于定權模型的研究，國內很多學者做了相關工作，如孫鵬[9]分析了等權模型、高度角模型、信噪比模型以及信號強度模型對BDS定位精度的影響，得到信噪比模型和信號強度模型定位精度較高，在兩個跟蹤站高差較大時，更適合使用高度角模型的結論；劉亞[10]等將SISER不同方式的衛星軌道與鐘差加入高度角定權模型，通過仿實時精密單點實驗驗證發現，該模型收斂時間減少了約0.91%，靜態精密單點定位（PPP）精度可達厘米級甚至毫米級；呂明慧[11]等聯合高度角和信噪比建立了全球化精細隨機模型，將該模型應用于高緯度PPP解算中，其定位精度比傳統的高度角和信噪比模型均有明顯提升，尤其是高程方向定位精度提升更明顯；錢妮佳[12]等提出了一種改進的信噪比隨機模型，并采用改進的隨機模型進行偽距單點定位解算，得到該模型的定位精度優于現存的幾種模型的結論；伍劭實[13]等提出了一種根據不同模型實時組建觀測量的隨機模型，該模型能真實反映各衛星觀測量的隨機噪聲特性，模糊度固定率和相對定位精度均有提升，更適合混合星座的BDS定位；蔣欠欠[14]等對比分析BDS、GPS、BDS/GPS系統在等權模型、高度角模型以及Helmert方差分量模型中的偽距PPP發現，組合系統定位精度優于單系統，Helmert方差分量模型定位精度最高，高度角模型次之，等權模型最低。綜上所述，國內學者對定權模型的研究主要集中在偽距與PPP方面，缺乏對相對定位的研究，因此本文以一組約10 km的短基線數據為實驗數據，對比分析了GPS、BDS、Galileo以及不同組合采用信噪比模型、高度角模型以及等權模型的相對定位精度。

1 數學模型

1.1 雙差定位模型

雙差定位模型是短基線相對定位的常用模型，一般表達式為[15-16]：

式中，s為參考衛星；k為非參考衛星；i為參考測站；j為非參考測站；為雙差偽距觀測值；為雙差載波相位觀測值；為測站至衛星間雙差幾何距離；λ為非參考星信號波長；為雙差整周模糊度；為雙差電離層延遲誤差；為雙差對流層延遲誤差；為雙差偽距觀測值噪聲；為雙差載波相位觀測值噪聲。

1.2 等權隨機模型

假設每顆衛星觀測值的精度相同且獨立，方差為σ0，構造n-1階方差—協方差矩陣，即

等權隨機模型可進一步表示為[14]：

式中，E為單位矩陣。

1.3 高度角隨機模型

高度角隨機模型就是對具有不同高度角的觀測值進行方差估計而得到的一種的驗前隨機模型。首先，計算得到站心坐標下E、N、U方向的坐標，計算公式為：

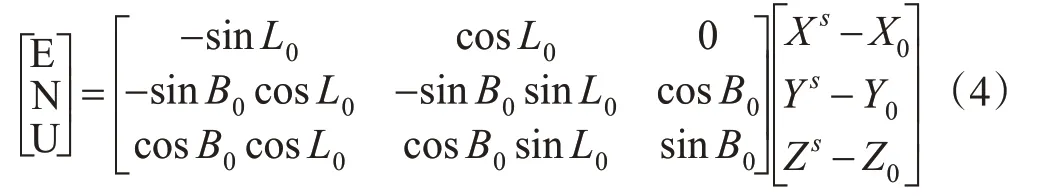
式中，L0、B0分別為測站的經緯度；(Xs，Ys，Zs)、(X0，Y0，Z0)分別為衛星和測站的空間直角坐標。

然后，求得衛星與測站之間的衛星高度角，計算公式為：

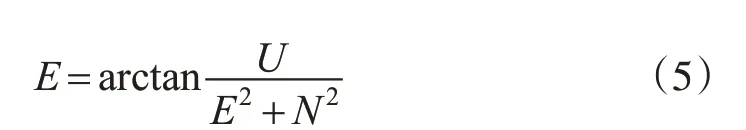
最后，利用正弦三角函數公式對不同高度角衛星的觀測值方差進行估計[14]，即

式中，E為衛星高度角；σ0為單位權方差。

1.4 信噪比隨機模型

采用信噪比建立的觀測值方差函數模型的一般表達式為：

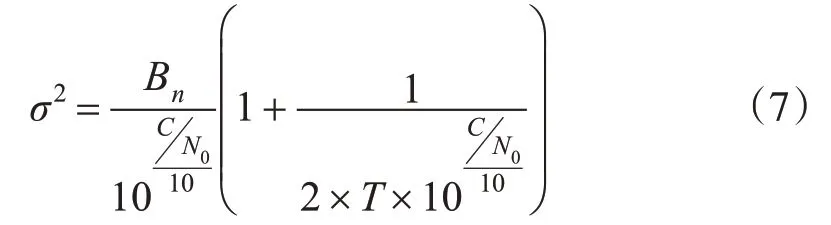
式中，Bn為載波相位跟蹤環的寬度值；T為一體化檢波的時間。

由于噪聲量級非常小，對式（7）進一步簡化，可得：

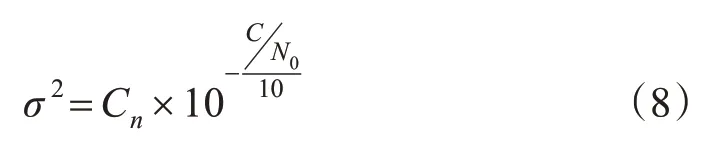
式中，Cn主要取決于接收機跟蹤通道得到的相位跟蹤環的寬度值；為信噪功率密度比值。

2 實驗分析

2.1 數據選取與解算策略

為詳細分析不同定權模型對短基線相對定位精度的影響，本文選取位于澳大利亞境內的兩個MGEX站組成的一組短基線作為實驗數據，測站分別為STR1和TID1站，基線長度約為10 km，數據采集時間間隔為30 s，采集時間為2021-04-21—2021-04-25。STR1站接收機類型為SEPT POLARX5，天線類型為ASH701945C_M；TID1站接收機類型為SEPT POLARX5，天線類型為AOAD/M_T；兩個跟蹤站均能接收GPS、BDS、Galileo信號。

數據解算軟件采用Net_Diff軟件，解算定權模型分別采用高度角定權、信噪比定權和等權模型，參與解算的GNSS系統分別為BDS、GPS、Galileo、BDS/GPS、BDS/Galileo、GPS/Galileo以及BDS/GPS/Galileo。

2.2 衛星可見性分析

各系統的衛星可見數如圖1所示，可以看出，雙系統組合衛星可見數多于任一單系統，三系統組合衛星可見數又多于雙系統組合；BDS平均衛星可見數為7顆，主要受限于接收機類型，GPS平均衛星可見數為8顆，Galileo平均衛星可見數為5顆，BDS/GPS組合平均衛星可見數為15顆，BDS/Galileo組合平均衛星可見數為15顆，GPS/Galileo組合平均衛星可見數為12顆，BDS/GPS/Galileo組合平均衛星可見數為20顆。各系統的PDOP值如圖2所示，可以看出，BDS和Galileo單系統的PDOP值較差，大部分歷元PDOP值大于3；雙系統和三系統組合衛星PDOP值較單系統有明顯改善，尤其是BDS/GPS/Galileo組合全部歷元的PDOP值均在2以內，平均PDOP值為0.87。

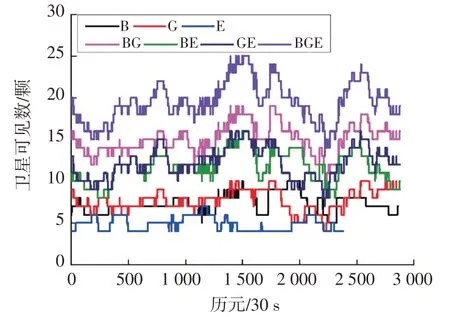
圖1 各系統衛星可見數統計

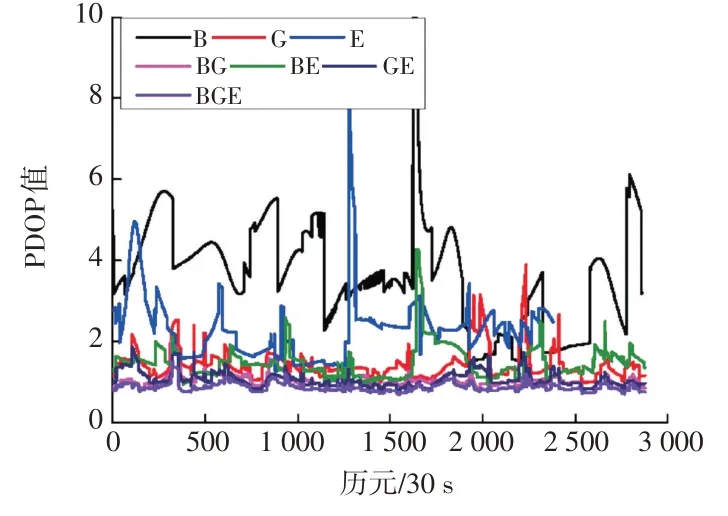
圖2 各系統PDOP值統計

2.3 定位精度分析

本文對不同解算策略的解算結果進行統計，以2021-04-23的解算結果為例，各系統采用高度角模型、等權模型和信噪比模型解算的基線誤差序列如圖3～9所示，可以看出，單系統短基線相對定位誤差較大，BDS與Galileo單系統短基線水平誤差部分歷元大于10 cm，甚至更大，部分歷元高程方向誤差大于20 cm，甚至更大，GPS單系統除部分歷元外，水平定位誤差在±5 cm以內，高程定位誤差在±10 cm以內；雙系統組合定位誤差較單系統有明顯減少，除少部分歷元外，水平定位誤差在±5 cm以內，高程定位誤差在±10 cm以內；三系統組合定位誤差又較雙系統有所減少，水平定位誤差在±5 cm以內，高程定位誤差在±10 cm以內；采用高度角模型解算的基線結果定位誤差較穩定且較小，其次為信噪比模型，等權模型定位誤差略大。

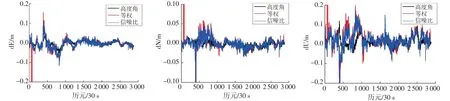
圖3 BDS單系統不同定權模型短基線解序列

圖4 GPS單系統不同定權模型短基線解序列

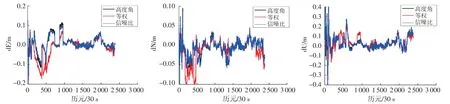
圖5 Galileo單系統不同定權模型短基線解序列

圖6 BDS/GPS組合不同定權模型短基線解序列

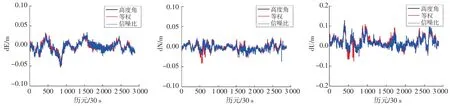
圖7 BDS/Galileo組合不同定權模型短基線解序列

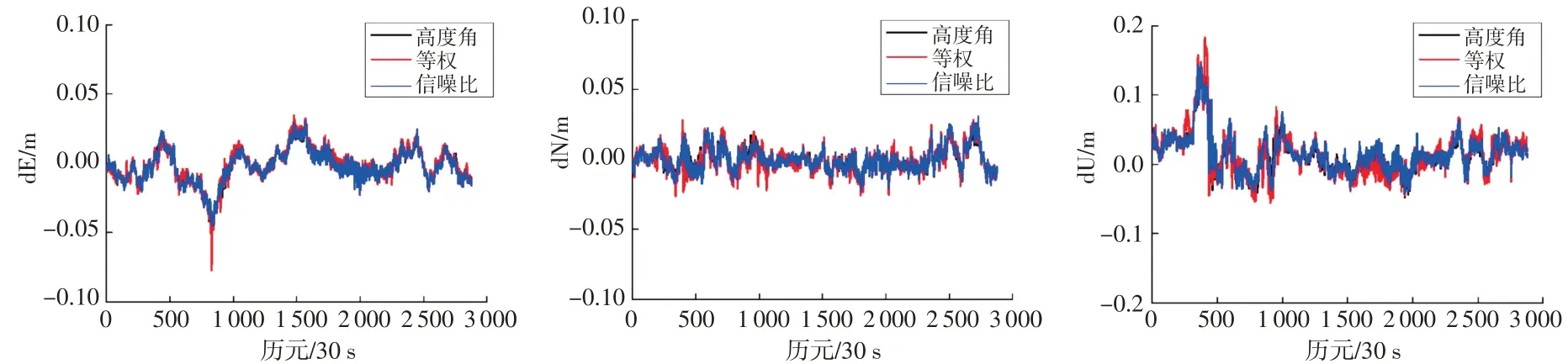
圖8 GPS/Galileo組合不同定權模型短基線解序列

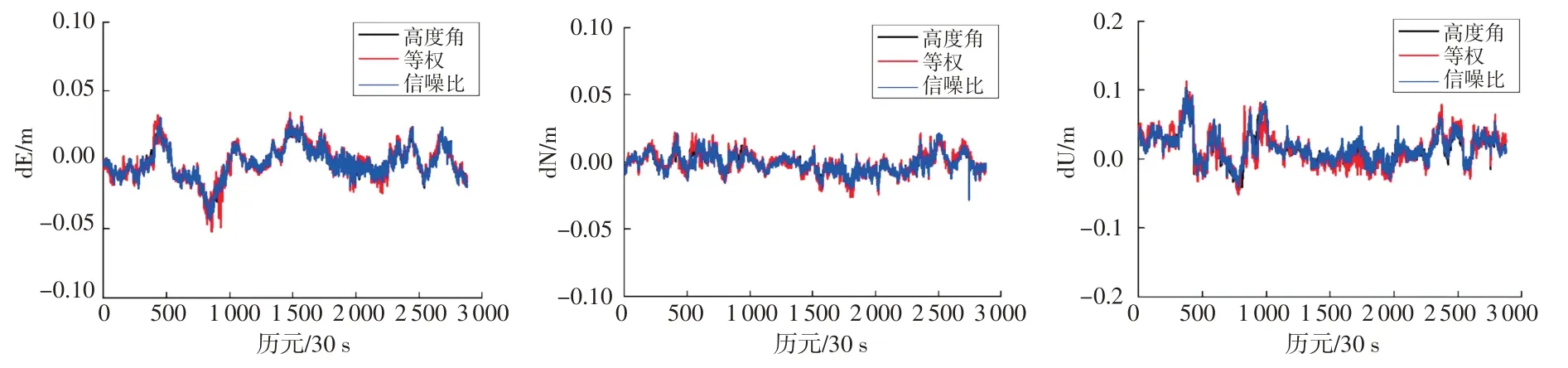
圖9 BDS/GPS/Galileo組合不同定權模型短基線解序列

為更加詳細分析不同定權模型對短基線相對定位精度的影響，本文進一步統計各系統采用高度角模型、等權模型以及信噪比模型解算的基線解多天定位精度，如圖10所示，可以看出，采用等權與信噪比模型解算的短基線定位結果略差，采用3種模型解算的短基線定位精度均低于其他系統，其余情況定位精度較好；E方向定位精度優于2 cm，N方向定位精度除GPS個別情況外均優于1 cm，U方向定位精度除等權模型外均優于3 cm，基線中誤差在4 cm以內；采用高度角模型解算的定位精度最優，信噪比模型次之，等權模型最差。

圖10 不同定權模型定位精度平均值

2.4 多系統組合較單系統定位精度提升定量分析

為進一步對比多系統組合較單系統短基線相對定位的優勢，本文進一步統計了雙系統和三系統組合相較于單系統定位精度的提升量平均值，如表1所示，可以看出，在3種定權模型下，雙系統和三系統組合較單系統定位精度均有明顯提升，尤其是三系統組合定位精度提升較明顯；對于高度角模型，三系統組合比BDS單系統定位精度在E、N、U方向分別提升了7.32%、13.16%、10.32%，比GPS單系統定位精度在E、N、U方向分別提升了2.56%、30.53%、23.39%，比Galileo單系統定位精度在E、N、U方向分別提升了72.40%、70.40%、73.51%；對于等權模型，三系統組合比BDS單系統定位精度在E、N、U方向分別提升了76.78%、72.38%、59.97%，比GPS單系統定位精度在E、N、U方 向 分 別 提 升 了10.79%、34.71%、23.29%，比Galileo單系統定位精度在E、N、U方向分別提升了75.25%、72.85%、69.09%；對于信噪比模型，三系統組合比BDS單系統定位精度在E、N、U方向分別提升了48.20%、46.88%、44.22%，比GPS單系統定位精度在E、N、U方向分別提升了2.54%、29.90%、23.59%，比Galileo單系統定位精度在E、N、U方向分別提升了70.21%、69.09%、75.48%；采用3種定權模型的雙系統和三系統組合定位精度相較于GPS和Galileo單系統提升量相當，采用等權模型的雙系統和三系統組合定位精度比BDS單系統提升量最大，采用信噪比模型次之，采用高度角模型最小。

表1 多系統組合相較于BDS、GPS、Galileo單系統定位精度的提升/%

綜合表1和圖10分析可知，Galileo單系統短基線定位精度較差，更適合與其他系統組合進行定位，而BDS和GPS單系統短基線精度相當且較高；定權模型對GPS和Galileo單系統和與其他系統組合定位性能的影響較小，對BDS單系統和與其他系統組合定位性能的影響較大。

3 結語

針對短基線相對定位解算定權模型的選擇問題，本文基于一組實測短基線數據，詳細分析了高度角模型、等權模型和信噪比模型在BDS/GPS/Galileo短基線相對定位解算中的應用，得到的結論為：①多系統組合能有效改善單系統衛星可見數較少和PDOP值過大的情況；②除個別情況外，BDS單系統短基線定位精度較優，定位精度可達厘米級，而Galileo單系統定位精度較差，雙系統和三系統組合定位精度較單系統均有明顯提升，尤其是三系統組合定位精度最為明顯，可為今后短基線相對定位系統選擇提供一定參考；③3種定權模型中，高度角模型定位精度最優，信噪比模型次之，等權模型定位精度最低，可為今后短基線相對定位定權模型選擇提供一定參考；④定權模型對GPS、Galileo及其相關組合定位影響較小，而對BDS及其相關組合定位影響較大。